역행렬

역행렬 (Inverse Matrix)

항등 행렬 (Identity Matrix)

• 선형 변환의 결과가 변함없는 행렬

• 두 표준 기저벡터 $e_1, e_2$의 값이 동일하게 유지되는 선형변환을 의미

역행렬이란?

• 선형 변환된 결과를 거꾸로 돌려부는 선형 변환

• 이를 합성한 결과는 항등 변환

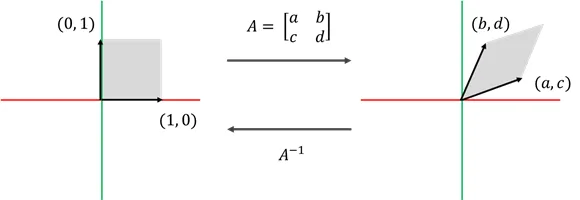
역행렬의 계산 방법

행렬식 (Determinant)

• 아래 연립방정식의 해는 존재?

• 위 연립방정식의 행렬식은 $2\cdot 0.5 - 1\cdot 1=0$이 나오고 이는 해가 없음을 의미

  • 어째서인가?
  • 위 식을 행렬로 나타내면 다음과 같음

• 위 변환을 분석하면 표준기저벡터 $e_1, e_2$는 각각 $(2,1), (1,0.5)$로 변환되었는데 이 둘은 같은 기울기를 가지고 있음

• 따라서 두 기저 벡터가 선형 독립에서 선형 의존 관계가 됨

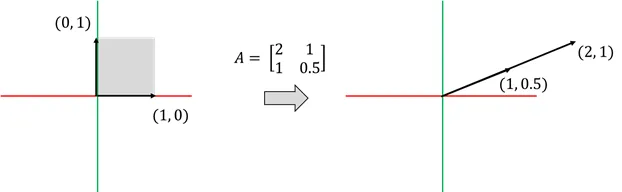
• 위의 경우 선형 변환의 결과로 2차원 평면이 1차원 직선으로 소멸되었기에 1차원에서 2차원으로 돌아가는 역행렬은 존재하지 않음

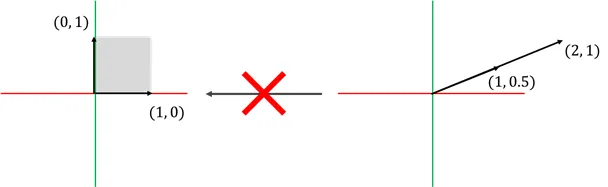
• 그렇다면 $ad -bc$가 0 일 때 차원이 소멸 되는 것인가?

• 두 벡터가 만드는 평행 사변형의 넓이는

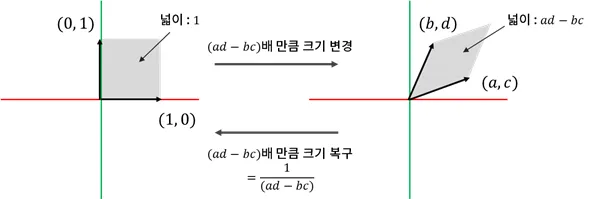
• 전체 사각형에서 남은 부피를 빼면 넓이 값은 $ad - bc$임

• 따라서 해당 넓이가 0 이라면 두 벡터가 동일한 기울기로 겹쳐 있게 됨

• 이는 선형 의존임을 의미

  • 만약 역행렬이 존재한다면?
  • 다음과 같은 변환을 생각하면 평면이 행렬식 값만큼 달라짐
  • 원상 복구 하기 위해서는 달라진 크기의 역수만큼 변해야 함

  

역행렬의 활용

• 연립방적식의 해를 구할 때 유용하게 사용
• 아래 식에서 선형 변환 $A$와 변환된 벡터 $v'$만 알고 있는 경우 $A$의 역행렬을 구할 수 있다면 양변에 곱해 변환하기 전의 벡터 $v$를 구할 수 있음

• 임의의 정방행렬의 역행렬을 구하기 위한 방법은 여러가지가 있는데 대표적으로 다음의 방법들이 존재

  • 가우스 소거법 ( Gaussian elimination )
  • 크라메르 공식 ( Cramer's rule)

• 하지만 우리가 사용하는 대표적인 선형 변환들은 위의 방법을 사용하지 않고 직관적으로 역행렬을 구하는 것이 가능

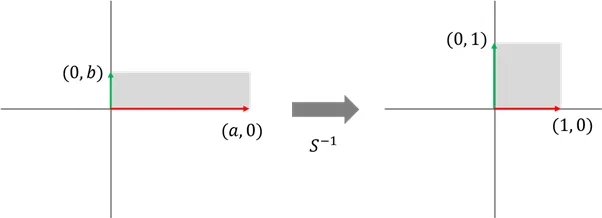
크기 행렬의 역행렬

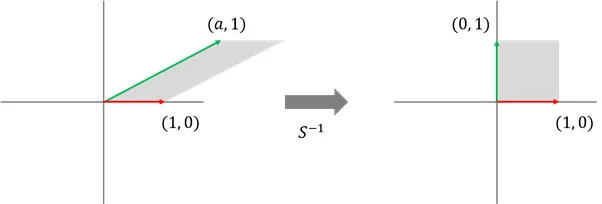
밀기 행렬의 역행렬

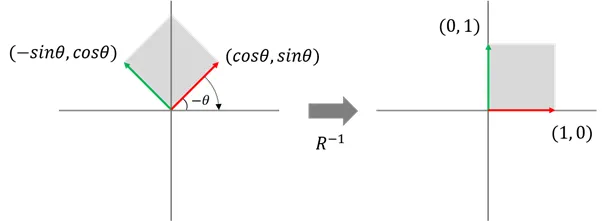
회전 행렬의 역행렬

• 위 결과에서 $R_\theta$ 와 $R_{(-\theta)}$는 서로 전치 관계를 이룸

• 따라서 회전 행렬의 역행렬은 전치 행렬이 됨