아핀공간

아핀 공간 (Affine Space)

이동 변환의 문제점

• 원점에서부터 시작하는 벡터의 특성상 기저벡터를 원점으로 부터 분리해 이동 불가

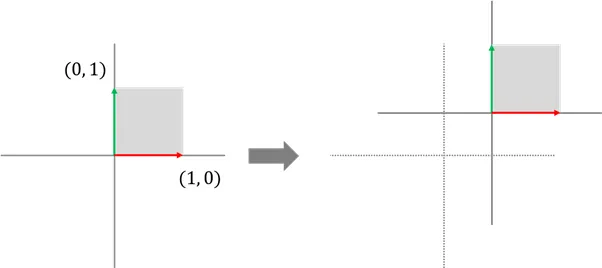
• 즉 다음과 같은 행렬은 존재 x

밀기 변환의 활용

• 하지만 밀기 변환을 활용하면 선형 변환의 형태로 이동을 구현하는 것이 가능

$x$ 값의 관찰

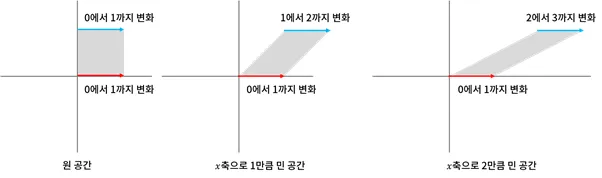
평면의 이동 변환

• 같은 원리로 3차원 공간에서 평면을 밀면 평면의 이동 구현이 가능

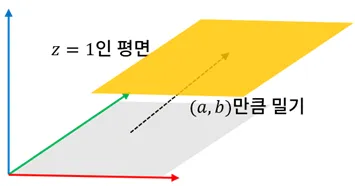
• 수식으로 나타내면 다음의 3차원 정방 행렬을 사용하면 원하는 만큼 2차원 평면의 이동 구현이 가능해짐

• 위와 같이 계산한 후 세 번째 요소는 버리면 이동 구현이 가능해짐

아핀 변환(Affine transformation)

• 점을 만들어내는 새로운 이동 변환

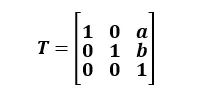
• 다른 변환들도 여기에 맞춰서 한 차원을 높이면 행렬곱으로 크기, 회전, 이동을 구현하는 것이 가능해짐

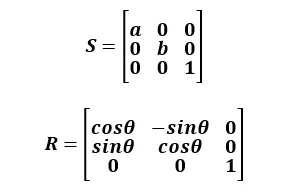
• 아래의 변환은 게임 제작에 필수적으로 사용되는 아핀 변환
  • 이동 (Translation)
  • 크기 (Scale)
  • 회전 (Rotation)

아핀 공간의 요소 (Affine Space Elements)

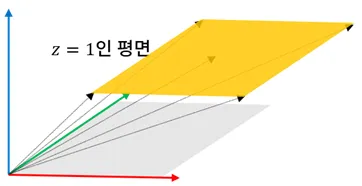
• 무대가 되는 벡터 공간에서 노란색을 구성하는 부분 공간을 아핀 공간으로 칭함
• 그리고 아핀 공간에 속한 원소를 따로 점 (Point)라고 함
• 점은 마지막 차원 값이 1인 특별한 유형을 가진 벡터를 의미

• 2차원 공간의 점 : $(x,y,1)$

• 3차원 공간의 점 : $(x,y,z,1)$

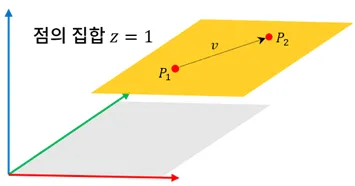
아핀 공간의 이동 벡터(변위 벡터)

• 점과 점의 대응 관계를 나타내기 위해서 사용하는 또 다른 종류의 벡터
• 점에 이동벡터를 더하면 다른 벡터를 생성 가능

• 2차원 공간의 점 : $(x,y,0)$

• 3차원 공간의 점 : $(x,y,z,0)$

• 이동 벡터의 마지막 차원 값은 0 이기 때문에 점에 이동 벡터를 더하면 마지막 차원의 값은 언제나 1을 보장 받음

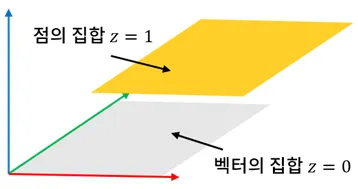
아핀 공간의 구성 요소

• 아핀 공간의 구성 요소
  • 점 : 물체의 시각적 표현을 위한 위치 정보
  • 이동 벡터 (벡터) : 점을 이동시키는 무형의 매개체

아핀 공간의 규칙

• 점 – 점 = 벡터

• 점 + 벡터 = 점

• 벡터 + 벡터 = 벡터

• 점 + 점 = 아핀 공간을 벗어나기 때문에 사용할 수 없음. ( 원하는대로 이동 불가능 )

• 이러한 규칙은 점에 대응되는 개념은 시각으로 벡터에 대응되는 개념은 시간 바꿔 설명 가능

• 점 - 점 = 시각 - 시각 : 3시 - 2시 = 1시간

• 점 + 벡터 = 시각 + 시간 : 3시 + 1시간 = 4시

• 벡터 + 벡터 = 시간 + 시간 : 2시간 + 3시간 = 5시간

• 점 + 점 = 시각 + 시각 : 2시 + 3시 = ??

아핀 공간의 의의

• 한 차원 높은 벡터 공간을 생성하고 이 안에서 아핀 공간을 활용해 이동을 구현할 수 있으며 아핀 공간 위에서 캐릭터가 움직이고 탐험 가능한 월드 공간의 기반이 만들어짐

• 월드 공간 위에서 배치하는 물체는 아핀 공간의 점을 사용해 구성되고 물체의 움직임은 이동 벡터를 활용해 구현

• 앞서서 배운 수학적 개념의 벡터와 구분하기 위해 이동 벡터로 불렀지만 이 이동 벡터는 바로 물리학에서 이야기하는 벡터의 개념과 동일