
1. The Moore-Penrose Pseudo Inverse [1]
행렬 의 Moore-Penrose inverse 는 역행렬을 일반화한 것임.
역행렬이 존재하지 않는 경우 (행렬식이 0)에도 유사한 역행렬을 구할 수 있도록 하는 것. (광범위한 형태의 역행렬)
→ 역행렬이 존재하는 경우 (가역)에는 pseudo inverse == inverse임. ()
앞으로는 특정한 언급이 없는 경우 pseudo inverse를 한다는 것은 Moore-Penrose inverse를 한다는 것을 의미함.
generalized inverse와 pseudoinverse는 같은 말임.
pseudoinverse는 “least squares”를 구할 때 많이 씀. → 오차가 가장 적은 best fit을 찾을 때
행렬의 모든 값이 실수/복소수로 구성되어 있는 경우 pesudoinverse는 유일함.
SVD를 사용하여 pseudoinverse를 구할 수 있음.
1-1. Pseudo-Inverse and Least Squares
least square는 “overdeterminded system”을 푸는 방법임. → 미지수의 개수보다 식의 개수가 더 많은 경우
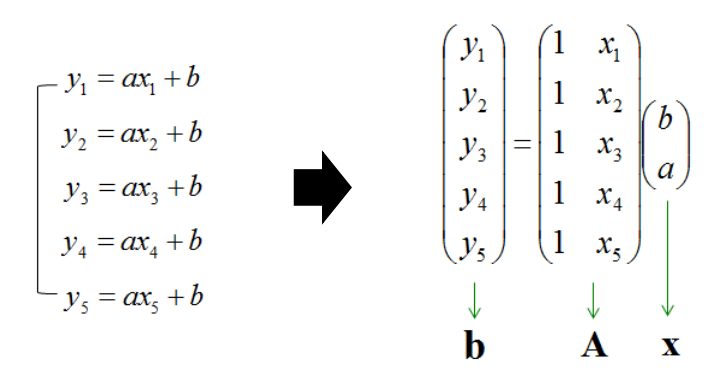
를 “관측값”이라고 하는데, 관측값이 많고, 이 함수가 linear라는 것을 확신할 때, 관측값 사이의 error를 최소화하는 방식으로 linear function을 찾는 과정이 least square
관측을 계속 하다 보면 error에 따라 기준값보다 커지거나 작아지는 일이 발생하는데, 이러한 error를 최소화하는 linear 식을 찾는 것.
작은 오브젝트 (점과 같은)가 평면 위에서 움직이고 있다고 가정함.
이 점이 직선 위에서 움직이고 있는 것 같다고 생각할 수 있고, 각각 에서 관측함. → 식에 대입
이때 error가 없으면 이 식을 풀 수 있는 상태가 되고, 식 2개만 있어도 풀 수 있음. but error가 있으면 이 식을 풀 수 없는 상태가 됨.
least square의 아이디어는 sum of the squares of the errors (SSE)를 최소화하는 것.
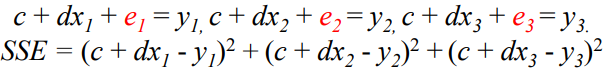
평면 위에서 움직이는 점을 와 같은 형태로 표현할 수 있음. (error 값 추가) → error는 여러 개 나올 수 있으므로 와 같은 벡터 형태임.
이때 를 최소화하는 것이 목표.
ex)
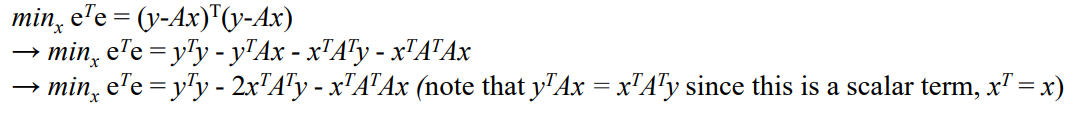
()
스칼라에서는
편미분을 해서 0이 되는 지점이 최솟값이 될 것. → [2]
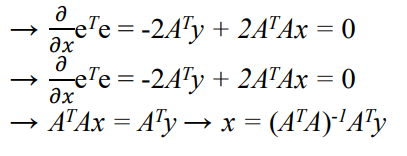
이때 의 형태였으므로 를 넘기면 가 됨. 따라서
⭐
Practice
Q. 다음과 같은 방정식이 있음.
이 방정식을 와 같은 행렬 형태로 쓸 수 있는데, 이때 의 Moore-Penrose Psudoinverse를 구하라. ()
A. , ⇒
1-2. Pseudo Inverse and SVD
least square 뿐만 아니라 SVD를 사용해도 pseudoinverse를 구할 수 있음. SVD를 사용해서 역행렬을 구하는 것을 먼저 볼 것임.
일 때, 직교 행렬 에서 로 표현할 수 있음. 이때 은 singular value의 대각행렬임.
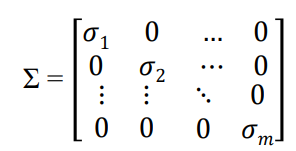
이때 는 singular value, 와 의 column을 각각 left singular vector & right singular vector라고 함.
는 직교행렬이기 때문에 inverse == transpose임. () 이를 통해 임을 도출할 수 있음. (원래는 )
이때 은 singular value의 역수에 대한 대각행렬임.
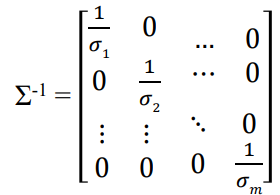
but 이 존재하지 않는 경우도 있음. (비가역)
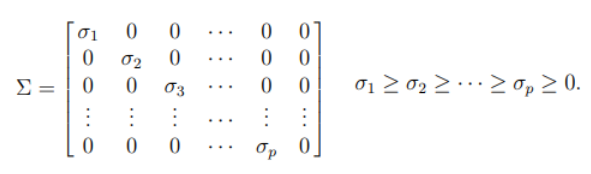
원래 에서 로 역행렬을 곱해서 의 값이 복원되어야 하는데, 대각행렬의 값이 0인 경우 어떤 값을 곱해도 0이 되기 때문에 “복원 가능”이라는 말이 성립하지 않음. (과 같은 논리)
따라서 “모든 값을 복원”하지 않고, 복원이 가능한 형태를 가진 값들만 최대한 복원하는 것이 pseudoinverse 임. (완화된, generalized inverse)
이라고 가정. (위에서보다 차원이 늘어남.) 으로 분해하여 처럼 쓸 수 있음.
이때 의 pseudoinverse 임. (원래 inverse와 동일하게 사용)

(과 형태는 유사하지만, invertible한 값만 invert한다는 것이 차이)
2. Jacobian Inverse Methods
2-1. Jacobian Pseudo-inverse
결국 우리는 IK에서 목표 지점이 주어졌을 때, 이에 지점에 도달하기 위한 joint angle을 각각 구해야 하고, 그 과정에서 Jacobian 행렬을 사용했었음.
즉, 을 풀어야 하는 것.
처음에 Jacobian을 얘기할 때 least-square 방식으로 푼다고 이야기했었는데, 결국 pseudo-inverse를 구하는 것이 값들의 error를 최소화하는 방향으로 진행하는 것이므로 Jacobian의 pseudo-inverse를 통해 IK를 풀 수 있음.
pseudo-inverse를 구하기 위해 이 식을 조작함.
→ 를 우변으로 넘기면 →
가 “full row rank”일 때에만 pseudo-inverse가 가능하며, 나 는 invertible함.
Full row rank?
행렬의 rank 일 때, 이 행렬은 full row rank를 가짐. 즉, 행렬의 각 row vector들이 서로 선형독립이면 full row rank를 가짐.
column rank → 서로 선형독립인 최대 column의 수
row rank → 서로 선형독립인 최대 row의 수
또한, column rank과 row rank 중 큰 값을 갖는 rank가 중에서 큰 값과 일치한다면 full rank라고 함.
3. Damped Least Squares (DLS) [3]
pseudo-inverse method의 문제점을 해결하기 위해 쓰이는 방법.
무슨 문제?

여기서 singular value가 0이 되면 문제가 발생함. (값이 무한대로 발산함)
DLS는 singular value가 0이 되는 것을 막기 위해 약간의 값을 더해줌.
Levenberg-Margquardt method라고도 하며, Wampler [5], Nakamura & Hanfusa [4]의 논문에서 처음 IK에 사용되었음.
DLS에서는 을 최소화함. → 이라는 새로운 값이 추가됨.
: non-zero damping constant. 직접 결정하는 경우도 있고, 자동으로 선택해주기도 함.
- damping constant를 잘 골라서 numerically stable하게 만들어야 함.
- damping constant가 너무 작으면 singular value가 0이 되어 발산할 위험이 있으므로 적당히 큰 값을 골라야 함.
- 너무 크면 convergence rate가 너무 느려짐. → 알맞은 해를 찾는데 오래 걸린다는 뜻
를 행렬로 쓰면 다음과 같음.
또한 normal equation 형태로 나타내면
Normal Equation?
Least Square Cost Function을 분석적으로 접근하기 위한 식. 앞서 least square에서 error를 최소화하려면 를 최소화해야한다고 했고, 여러 식을 거쳐 최종적으로 또는 라는 식이 나왔는데, 이 식이 normal equation임.
이때 를 normal matrix라고 함.
위 식을 다시 정리하면
DLS에서는 가 non-singular이기 때문에 solution을 다음과 같이 쓸 수 있음.
(두 가지 form 모두 가능함. 보통 뒤에 있는 식을 사용함 → 가로로 긴 행렬보다는 세로로 긴 행렬을 쓰는 것이 효율적이기 때문)
3-1. Pseudo-inverse Damped Least Squares
를 구해야 하는데, SVD를 통해 구할 수 있음. ()
가 행렬일 때, 는 , 은 , 는 행렬임.
- 는 orthogonal matrix이기 때문에
- 는 diagonal matrix이며, 대각선에는 singular value 이 있음.
- 는 행렬이며, 대각선에는 singular value의 제곱 이 있음.
따라서 이며, 는 대각선 값이 인 diagonal matrix임. (는 상수)
결국 을 구해야 하는데, 이는 다음과 같이 계산할 수 있음.
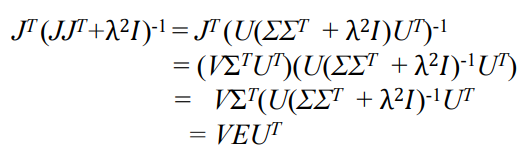
: 대각선 값이 인 diagonal matrix
결론적으로, DLS의 solution은 다음과 같음.
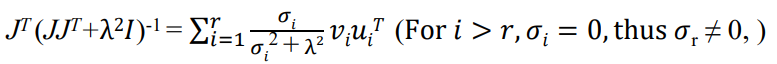
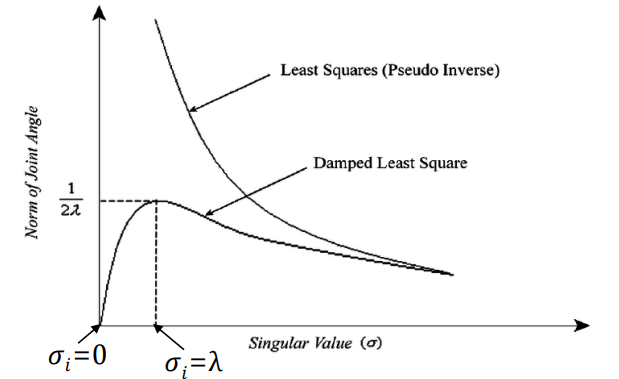
<DLS vs pseudo-inverse>
- 가 0으로 가면 값이 무한대로 발산하는 pseudo-inverse와는 달리, DLS는 을 통해 값이 0이 되지 않도록 보호하기 때문에 numerically stable함.
- 가 충분히 커지면 은 와 거의 비슷해짐. 즉, singular value가 충분히 커서 singularity problem에서 멀어지면, least square 방식과 pseudo-inverse는 동일하게 작동함.
- but, 가 작아지면서 0에 수렴할수록 DLS와 pseudo-inverse는 확연한 차이를 보임.
4. Performance Comparison
4-1. Jacobian Transpose vs. Jacobian DLS vs. Jacobian SVD-DLS [6]
Jacobian Transpose는 Jacobian pseudo-inverse와 비슷하지만 numerically easy하기 때문에 사용하는 알고리즘임.
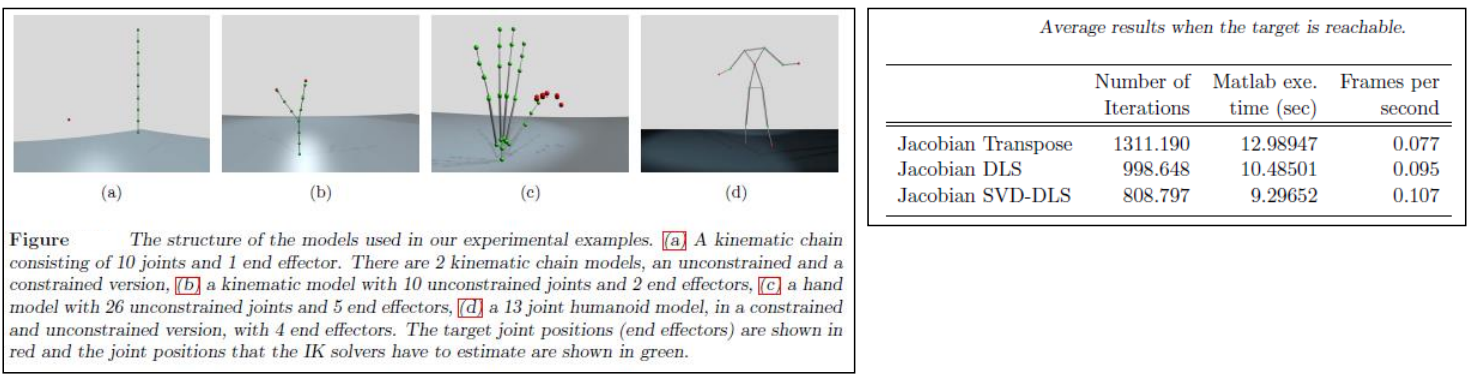
SVD-DLS로 갈수록 iteration이 줄어드는데, “적은 iteration으로 원하는 목표에 도달할 수 있다”는 것을 의미함.
실행 시간 또한 SVD-DLS가 가장 짧은 것을 볼 수 있음.
Frames per second는 1프레임을 그리는 데 걸리는 시간을 의미하며, 단순 pseudo-inverse의 속도가 가장 빠름을 알 수 있음.
(이 기술들은 다소 old한 기술들임)
Reference
[1] https://en.wikipedia.org/wiki/Moore%E2%80%93Penrose_inverse
[2] https://economictheoryblog.com/2015/02/19/ols_estimator/
[3] http://www.cs.cmu.edu/~15464-s13/lectures/lecture6/iksurvey.pdf
[4] Y. Nakamura and H. Hanafusa, Inverse kinematics solutions with singularity robustness for robot manipulator
control, Journal of Dynamic Systems, Measurement, and Control, 108 (1986), pp. 163–171.
[5] C. W. Wampler, Manipulator inverse kinematic solutions based on vector formulations and damped least squares
methods, IEEE Transactions on Systems, Man, and Cybernetics, 16 (1986), pp. 93–101.
[6] Inverse Kinematics: a review of existing techniques and introduction of a new fast iterative solver, University of
Cambridge, Andreas Aristidou and Joan Lasenby, 2009

시험공부하는데도움이됐습니다