1. Introduction
1-1. Newton Methods [1]
Newton Method는 object function f(x)의 2차 테일러 급수를 기반으로 함.
f(x+σ)≈f(x)+[∇f(x)]Tσ+21σTHf(x)σ (≈ : 근사. approximation)
Hf(x)는 f의 Hessian Matrix임. (multi-variative 함수의 2차 미분)
하지만 Hessian matrix를 그대로 계산하는 것은 computational cost가 크고 복잡하기 때문에, 직접 계산하지 않고 꼼수를 써서 Hessian matrix의 근사값을 구하는 방법이 존재함. → gradient value를 기반으로
잘 알려진 method로는 Broyden’s method, Powell’s method, Broyden-Fletcher-Goldfarb-Shanno (BFGS) method 가 있음.
<Newton Method의 장단점>
- 장점
- erratic discontinuity 없이 부드러운 모션을 만들어낼 수 있음.
- singularity problem에 구애받지 않음. (object function을 향해 수렴하는 형태이기 때문. Jacobian은 분모가 0이 되어 무한대로 발산하는 문제가 발생했었음)
- 단점
- 구현하기 힘듦.
- 각 iteration마다 엄청난 양의 computational cost를 요구함. (오버헤드가 큼)
2. Basics
2-1. Taylor Series [2]
함수가 “무한대로 미분가능 (infinitely differentiable)”하다고 가정하면, 테일러 급수 (Taylor Series)라는 power series를 만들 수 있음.
Power Series? [3]
다음과 같은 형태를 갖는 무한급수.
∑n=0∞an(x−c)n=a0+a1(x−c)+a2(x−c)2+⋯
(이때 an은 n번째 식의 계수, c는 상수값)
power series의 특수한 형태가 테일러 급수라고 볼 수 있음.
함수 f(x)를 근사하기 위해 특정 점 f(a)에서 근사를 진행함. (점에 가까워질수록 원본 함수와 비슷한 형태를 띠고, 멀어질수록 원본의 형태와 달라짐)
f(x)=f(a)+1!f′(a)(x−a)+2!f′′(a)(x−a)2+3!f′′′(a)(x−a)3+⋯=∑n=0∞n!fn(a)(x−a)n → 테일러 급수
a=0인 경우, 이 급수를 Maclaurin series (맥클로린 급수)라고 하며, 다음과 같음.
f(x)=f(0)+f′(0)x+2!f′′(0)x2+3!f′′′(0)x3+⋯+n!f(n)(0)xn+⋯
2-2. Gradient [4]
multivariable function f(x,y,…)에서 Gradient란 ‘각 파라미터에 대한 편미분으로 이루어진 벡터’이며, ∇f로 표기함.
∇f=⎣⎢⎢⎡∂x∂f∂y∂f⋮⎦⎥⎥⎤
ex) f(x,y)=2x2−4xy ⇒ ∇f=[4x−4y−4x]
<gradient의 기하학적 의미>
특정 점 (x0,y0,…)에 서있을 때, ∇f(x0,y0,…)는 “어느 방향으로 가야 함수가 가장 빠르게 증가하는지”에 대한 것임.
즉, 각 파라미터에 해당하는 방향으로 가장 빠르게 이동할 수 있는 벡터가 gradient인 것.
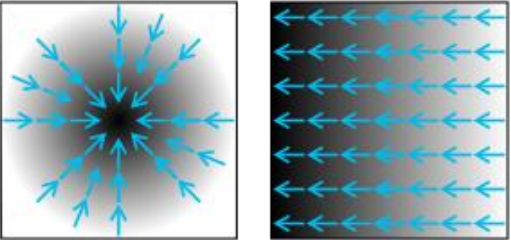
∇f는 위 그림처럼 vector field로 나타낼 수 있음. → gradient : 파란색 화살표
그림에서 보면 gradient는 “함수가 가장 크게 변하는 방향의 벡터”를 나타내고 있고, 하얀색에서 검은색으로 갈수록 값이 증가한다는 것을 의미함. [5]
2-3. Interpreting the gradient [4]
gradient의 기하학적인 해석.
input f가 2차원이라고 가정하고, (x0,y0) 점에서의 gradient를 다음과 같이 표현할 수 있음.
∇f(x0,y0)=[∂x∂f(x0,y0)∂y∂f(x0,y0)]
이렇게 되면 이 벡터는 점 (x0,y0)에서의 동작을 나타내게 됨.
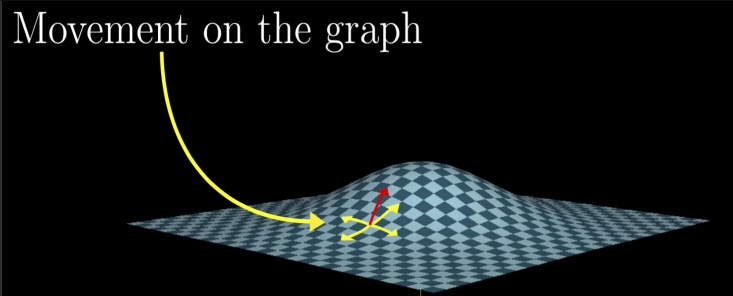
위 그림에서 (x0,y0) 점 위에 서있다고 가정.
이때 곡면 위를 “걷는다”는 것은 언덕의 slope를 따라서 걷는 것이라고 할 수 있고, y-direction으로 걷고 있는 경우 ∂y∂f의 slope로 걷고 있다는 것을 의미.
gradient vector의 방향으로 걷는다는 것은 “가장 빠르게 언덕을 올라갈 수 있는 방향으로 걷고 있다.”는 뜻.
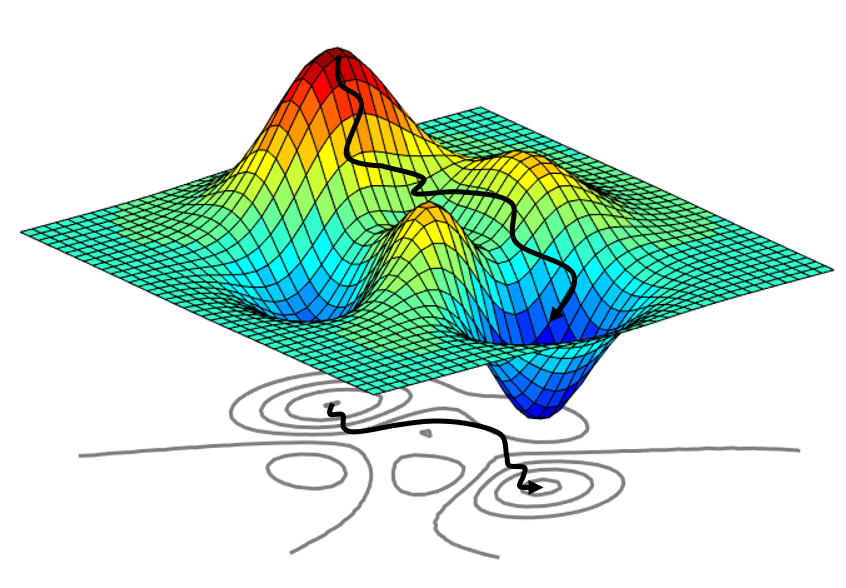
2-4. Hessian [6]
scalar-valued function의 2차 편미분을 element로 한 Square Matrix
(Hf)i,j=∂xi ∂xj∂2f
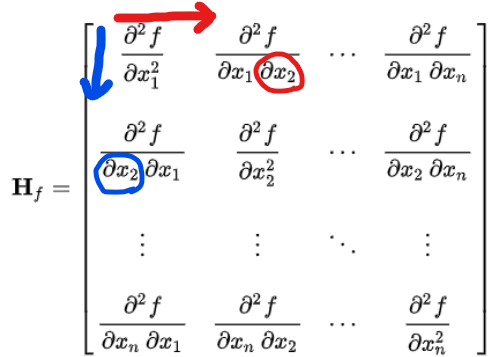
Hf(x,y,z)=⎣⎢⎢⎡∂x ∂x∂2f∂y ∂x∂2f∂z ∂x∂2f∂x ∂y∂2f∂y ∂y∂2f∂z ∂y∂2f∂x ∂z∂2f∂y ∂z∂2f∂z ∂z∂2f⎦⎥⎥⎤
벡터 x를 input으로 받아서 스칼라 f(x)∈R을 반환하는 함수 f:Rn→R이 있다고 가정. (f(x,y,z))
- f의 모든 2차미분이 미분가능하고 연속일 때, Hessian matrix H는 n×n square matrix임. ((x,y,z) → 3x3 matrix)
- 편미분은 순서 상관 없이 ∂x∂y=∂y∂x이므로 Hessian matrix는 대칭 행렬임. → SVD로 쉽게 바꿀 수 있음.
- Hessian matrix의 행렬식을 Hessian determinant라고 함. → 뭔가를 증명할 때 많이 쓰임.
- 함수 f의 Hessian matrix는 f의 “gradient의 Jacobian matrix”임.
- 즉, H(f(x))=J(∇f(x))
Practice
Q1. 점 (3, −3, 2)에서 x2y+4zex+y=f(x,y,z)의 gradient vector를 구하라.
A. ∇f=⎣⎢⎢⎡∂x∂f∂y∂f∂z∂f⎦⎥⎥⎤=⎣⎢⎡2xy+4zex+yx2+4zex+y4ex+y⎦⎥⎤
⇒ (3, −3, 2) → (−12, 5, 4)
Q2. F(x,y)=ln(x)ln(y)일 때, F의 Hessian은?
A. HF=[∂x∂x∂2F∂y∂x∂2F∂x∂y∂2F∂y∂y∂2F]=[−x2ln(y)xy1xy1−y2ln(x)]
2-5. Jacobian and Hessian
⭐H(f(x))=J(∇f(x))⭐
f(x,y)=x3+2x2y+3xy+4y3에서의 H(f(x))를 구해보자.
- ∂x∂f=3x2+4xy+3y, ∂y∂f=12y2+2x2+3x (1차 편미분)
- ∂2x∂2f=6x+4y, ∂2y∂2f=24y, ∂x∂y∂2f=∂y∂x∂2f=4x+3 (2차 편미분)
- ∴[∂2x∂2f∂y∂x∂2f∂x∂y∂2f∂2y∂2f]=[6x+4y4x+34x+324y]
같은 함수에 대해 J(∇f(x))를 구해보자.
- ∂x∂f=3x2+4xy+3y, ∂y∂f=12y2+2x2+3x (1차 편미분)
→ ∇f(x,y)=[∂x∂f(x,y)∂y∂f(x,y)]=[3x2+4xy+3y12y2+2x2+3x]
-
J(⎣⎢⎡f1f2f3⎦⎥⎤)=⎣⎢⎢⎡∂x∂f1∂x∂f2∂x∂f3∂y∂f1∂y∂f2∂y∂f3∂z∂f1∂z∂f2∂z∂f3⎦⎥⎥⎤ (Jacobian의 정의)
-
J([∂x∂f∂y∂f])=[∂2x∂2f∂y∂x∂2f∂x∂y∂2f∂2y∂2f]=[6x+4y4x+34x+324y]
⇒ 따라서 H(f(x))=J(∇f(x))
3. Newton-Raphson Method
3-1. Newton-Raphson Method (also known as Newton method) and IK
IK의 목표는 sd−f(θ)=0을 만족하는 joint angle θ를 구하는 것이었음. (sd : end effector의 desired position)
위 식의 solution을 θd (desired theta)로 표현할 수 있음. 해를 구하는 과정에서 Newton method를 적용할 수 있고, 이는 곧 root finding method임.
(root finding → 특정 함수값을 알고 있을 때, 출력값이 0이 되는 input를 찾아나가는 과정)
- 처음에는 초기값 θ0를 설정함. (추측값. initial guess)
- 이에 따라 sd−f(θ0)를 계산할 수 있음.
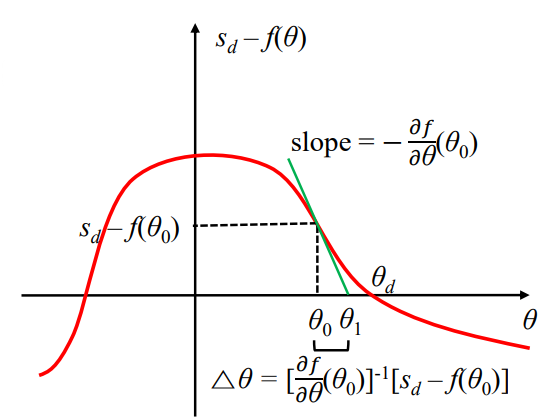
- θ0이 함수와 만나는 지점에서의 slope (기울기)를 미분을 통해 구할 수 있음. −∂θ∂f(θ0). 이 기울기가 θ축과 만나는 지점을 θ1으로 설정함.
- slope = θ1−θ0f(θ1)−f(θ0)
- θ0를 θ1으로 만들기 위한 Δθ가 존재함. Δθ=[∂θ∂f(θ0)]−1[sd−f(θ0)] (1 / 편미분 * 원래 함수)
⇒ 이 과정을 반복하다보면 점이 θd에 가까워짐.
<Newton method의 단점>
- 함수의 형태가 복잡한 경우 guessing이 제대로 되지 않음.
- 초기값이 desired value에서 너무 먼 경우 guessing이 제대로 되지 않음.
Practice
Q. Newton-Raphson method를 사용하여 초기 estimation에서의 one-step improvement를 찾아라.
Q1. f(x)=ex−4, initial estimate x0=1.5
Q2. g(x)=x3−2x−4, initial estimate x0=2.5
A.
Q1. slope = −f′(x0)
Δx=x1−x0=−f′(x0)f(x0)
∂x∂f=ex
Δx=exex−4
(update function : x1=x0−Δx)
(update function을 x0+Δx로 정의할 수도 있고, x0−Δx로 정의할 수도 있음)
∴x1=1.5−e1.5e1.5−4
Q2.
∂x∂g=3x2−2
∴x1=x0−g′(x0)g(x0)=2.5−3×(2.5)2−2(2.5)3−2×(2.5)−4
Reference
[1] http://www.cs.cmu.edu/~15464-s13/lectures/lecture6/iksurvey.pdf
[2] https://machinelearningmastery.com/a-gentle-introduction-to-taylor-series/
[3] https://en.wikipedia.org/wiki/Power_series
[4] https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives/partial-derivative-andgradient-articles/a/the-gradient
[5] https://en.wikipedia.org/wiki/Gradient
[6] https://en.wikipedia.org/wiki/Hessian_matrix






