
1. Cyclic Coordinate Descent (CCD) [1]
FABRIK 등장 이전에 많이 쓰이던 방식.
1-1. Iterative Heuristic Search
CCD는 articulated body의 interactive control을 수행하기에 좋은 heuristic 기술임. (== IK에 좋다)
- CCD method는 position과 orientation 에러를 줄이기 위해 하나의 joint variable을 한 번의 iteration마다 transform함.
- end effector에서 시작하여 base로 향해가면서 end effector가 target에 가장 가깝게 있을 수 있도록 joint를 조절함.
- 만족스러운 값이 나올때까지 계속해서 반복함.
- computational cost가 매우 적기 때문에 IK에서 활용할 수 있음.
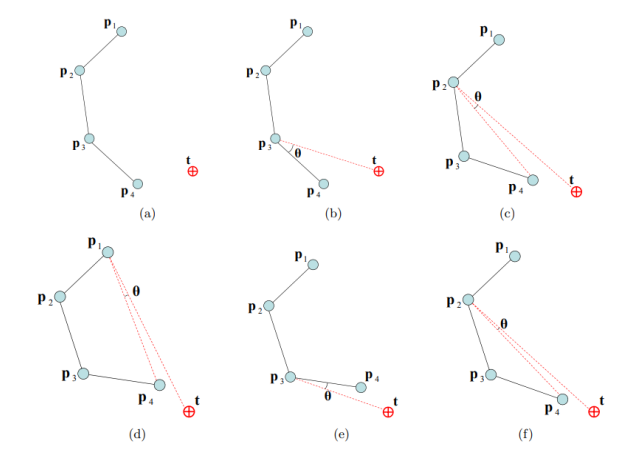
→ end effector에서 출발하여 위로 올라가면서 target과의 직선을 긋고, end effector와의 각 가 0이 되도록 end effector를 옮기고, 이를 다른 joint들에 대해 반복함.
2. Triangulation IK [2]
2-1. Law of Cosines for IK
제2 코사인 법칙을 통해 IK를 해결하는 방식.
root에서 출발하여 end effector에 이르기까지 진행하는 방식임.
- “unconstrained joint를 사용하고 target이 범위 안에 있다”는 조건만 있으면 solution을 구할 수 있음이 보장됨.
→ 조건 자체가 말이 안됨. unconstrained joint라는 것은 팔 관절이 180도 돌아간다는 뜻이고, target이 범위 밖에 있어서 아무리 팔을 뻗어도 닿지 않는 경우에는 해를 구할 수 없음. → 문제점
현실에서의 신체는 constraint가 존재하고, target이 닿을 수 없는 범위에 있더라도 target을 향해 다가가는 모션을 보여줘야 함.
- iteration이 없이 동작하기 때문에 CCD보다 computational cost가 적어 속도가 빠름.
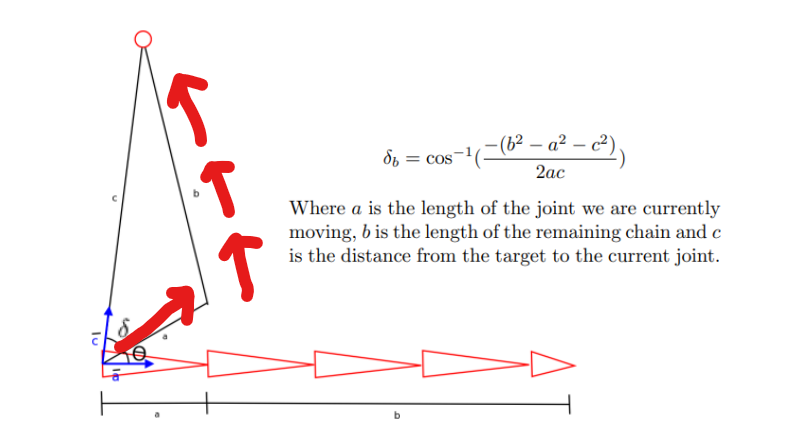
도달해야 하는 거리 에 도달하기 위해 를 어떻게 움직여야 하는지를 수식으로 정의하고, 이 수식을 풀어서 위치를 구함.
하지만 이 방법을 사용하면 다음과 같은 결과가 나올 수도 있음.
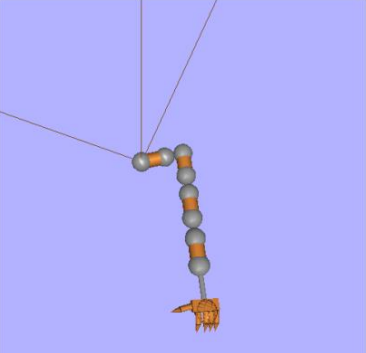
(뭐 왜 뭐. 문제 없이 잘 했잖아 뭐)
IK의 목적은 달성했으나, 현실성 제로. → 큰 단점
- end effector에 가까워질수록 joint가 직선을 이루고, root 근처에 있는 joint들은 거의 90도로 꺾여있음.
- 단점2 → end effector가 하나인 경우에만 사용할 수 있음. → end effector가 여러 개인 캐릭터 모델에는 사용할 수 없음. (로봇팔이라면 모를까)
- 단점3 → constraint를 주게 되면 해를 찾지 못함.
- joint 사이의 길이만 고려했을 뿐, 최대 회전 각도 등 추가적인 정보를 고려하지 않았기 때문에 이러한 상황이 발생하는 것.
3. Sequential Inverse Kinematics (SIK) [3]
3-1. Sequential Analytic-iterative IK
3차원 human full-body movement를 적용하기 위한 iterative method.
→ wrist, ankle, head, pelvis 등 여러 개의 end effector를 input으로 사용할 수 있음. (low-cost 모션캡쳐 데이터를 통해 human pose를 만드는 듯)
<Procedure>
- root joint의 위치와 orientation을 결정한다.
- root (허리)와 head를 이은 spine (척추)를 만든다. → 가장 중요한 부위
- 다음으로 중요한 부위인 쇄골, 골반 등을 만든다.
- 나머지 세부적인 joint들은 기존 IK 방법을 통해 만든다.
생물학적으로 각 joint를 고려하여 가장 그럴듯한 신체 포즈를 만들어냄.
SIK 또한 여러 번의 iteration을 돌면서 더 좋은 포즈를 만들어냄.
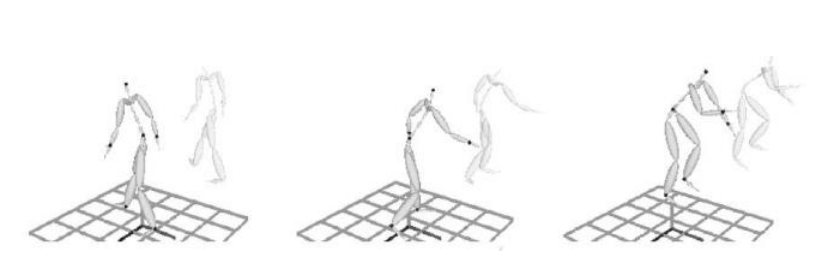
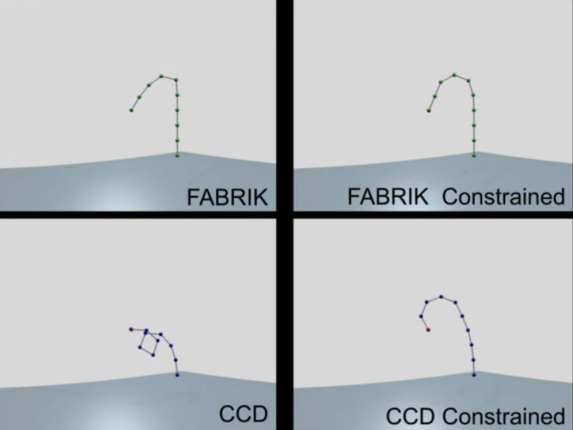
4. FABRIK
언리얼 엔진에서 실제로 쓰이고 있는 방식.
4-1. A fast, iterative solver for the Inverse Kinematics Problem
Forward and Backward Reaching Inverse Kinematics (FABRIK)
- FABRIK은 forward와 backward mode를 번갈아가면서 업데이트를 수행함.
- 각 joint angle을 한 번에 적용하여 system error를 최소화하는 것을 포함함.
- last joint of the chain에서 시작하는데, end effector에서 출발하여 backward로 한 번, 다시 forward로 end effector로 돌아오고 나면 iteration이 끝남.
- angle rotation을 구하지 않고 joint location을 구함으로써 iteration도 적게 돌고, computational cost도 적으며, 보다 현실적인 포즈를 만들어낼 수 있음.
- FABRIK은 언리얼, 유니티 등에 적용되어 사용되고 있음.
FABRIK을 구체적으로 알아보기 전에 몇몇 파라미터를 먼저 정의함.
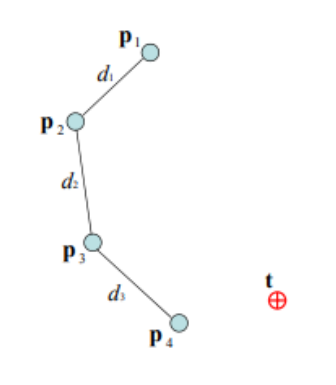
- : joint positions
- 을 root joint라고 가정하고, 을 end effector라고 가정함. 간단하게 하기 위해 end effector가 한 개인 상황을 가정함.
- : target. : 초기의 base position
- 1개의 target과 4개의 joint가 있는 상황
<procedure>
- 각 joint 사이의 길이를 구함. ()
- target이 reachable인지 확인함.
- root joint에서 target까지의 거리를 구함. ()
- inter-joint 간의 거리의 합 ()이 이면 reachable, 이면 unreachable
- target이 reachable하면 full iteration은 두 개의 스테이지로 나뉨.
- 첫 번째 스테이지
- 알고리즘은 end effector 에서 시작하여 base 으로 이동함.
- end effector를 target position으로 “강제로” 옮김. →
- 과 을 가로지르는 직선 을 찾는다.
- 번째 joint를 위에 강제로 옮긴다. () 이때, 으로부터 만큼 떨어진 곳에 위치시킨다.
- 위 작업을 반복한다.
- root를 포함한 모든 joint의 위치가 결정될 때까지 반복한다.
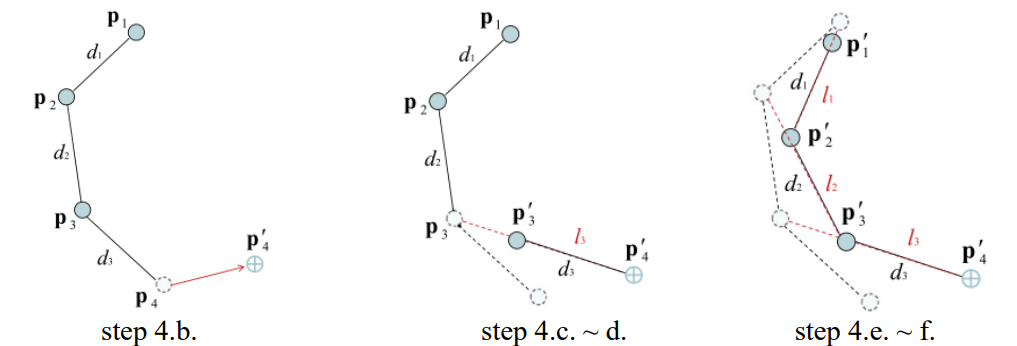
그런데, 이 과정에서 문제가 발생함. → root joint의 위치가 바뀌었음. (목표를 향해 움직이는데 팔이 뽑힌다?)
이를 해결하기 위해 한 번 더 iteration을 수행함.
- 두 번째 스테이지
- 첫 번째 스테이지와 동일한 과정을 root → end effector로 진행함.
- root joint를 원래 위치로 되돌려놓는다. →
- 과 을 잇는 직선 을 찾고, 을 으로부터 만큼 떨어져 있는 직선 위의 위치로 이동시킨다.
- end effector에 도달할 때까지 계속 반복한다.
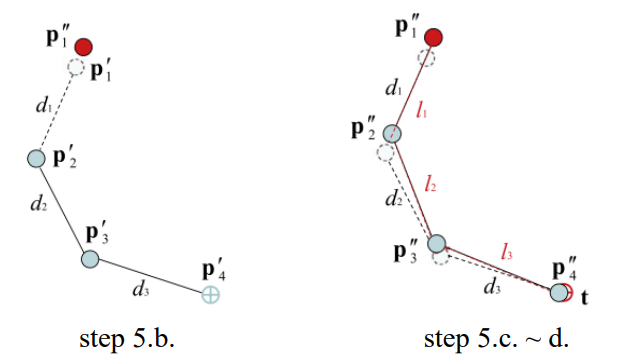
- 한 번 iteration을 돌고 나면 대부분 end effector는 target에 매우 가까운 상태가 됨.
- end effector와 target 간의 거리를 비교하고, 충분히 둘 사이의 거리가 가까우면 iteration을 멈추고, 아니면 iteration을 계속 진행함.

FABRIK은 multiple end effector에도 적용됨.
- 현실에서 hands, human or legged body 등과 같은 multibody model은 여러 개의 kinematic chain으로 이루어져 있으며, 각 체인은 일반적으로 1개 이상의 end effector를 가짐.
- 따라서 IK solver는 multiple end effector에 대한 solution도 제공해야 함.
- FABRIK은 매우 쉬운 방법으로 이를 제공함.
- 다만 sub-base joint와 chain의 개수 및 구조 등 모델에 대한 선행지식이 필요함. → 게임의 경우 기본적으로 모델에 대한 정보를 갖고 있기 때문에 문제가 되지 않음.
- sub-base joint란 2개 이상의 chain과 연결된 joint를 말함. (ex. pelvis)
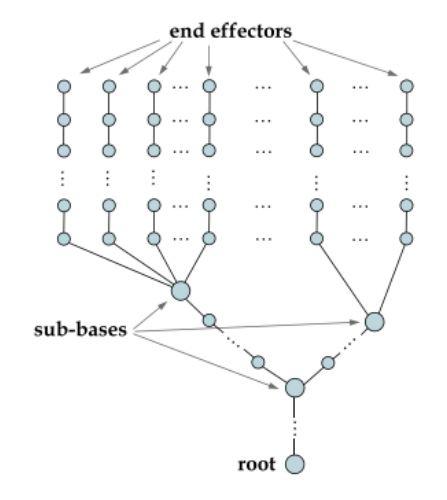
<FABRIK with multiple end effectors>
single end effector에서처럼 두 개의 스테이지로 나뉨.
(First Stage)
- 앞선 알고리즘을 그대로 적용하되, 각각의 end effector에서 출발하여 parent sub-base joint로 이동함.
- sub-base가 여러 개의 end effector와 연결되어있기 때문에 가능한 position이 많아지게 됨. → 어떤 end effector에서 보면 이쪽이고, 다른 end effector에서 보면 또 다른 쪽에 있어야 하고,,
- 따라서 새로운 position을 결정할 때, 가능한 모든 position을 더해서 한 가지로 결정함.
- 이후 기존 알고리즘에 의해 sub-base에서 출발하여 전체 root까지 동작함.
(Second Stage)
- 반대로, root에서 출발하여 sub-base로 이동함.
- 그런 다음 각 체인에 독립적으로 적용되어 end effector에 도달할 때까지 진행함. sub-base가 더 존재하는 경우 동일한 프로세스를 적용함.
- 모든 end effector가 target에 도달했거나 target과의 차이가 별로 없는 경우 iteration을 종료함.
<FABRIK의 문제점, 한계점>
- 실제 articulated body에는 “구동 가능 범위”가 존재하는데, FABRIK은 이를 고려하지 않고 무작정 position을 옮기고 있음. → 결과가 현실적으로 보이지 않을 가능성
- 이 문제는 쉽게 해결 가능함. → 어차피 iteration 돌려가면서 해를 찾는 과정이므로 처음에 구한 해가 구동 가능 범위 바깥에 있는 경우 구동 가능 범위 안으로 들어가면서 가장 그럴듯한 해를 찾는 iteration을 돌리면 됨.
- re-positioning & re-orientation : joint를 이동시키는데, 구동 가능 범위 내에서만 움직일 것
- 3D 문제를 2D 문제로 간단화해서 풀기 때문에, 복잡도와 처리 시간이 줄어듦.
- orientational limit을 갖는 ball-and-socket joint가 있다고 가정하고, 이를 rotor 과 rotational limit이 정해져 있는 가 있다고 가정
- joint의 구동 범위를 시각적으로 표현하면 찌그러진 cone 형태가 될 것임.
- 3가지 종류의 conic section이 만들어지게 됨.
- 가동 범위를 제한하는 모든 가 같다면, 가동 범위를 나타내는 conic section은 “원”의 형태가 됨.
- 가 90도보다 크거나 작고 같지 않다면 conic section은 “타원” 형태임.
- 모든 가 90도보다 크고 작으면 conic section은 “포물선” 형태임. (큰 애들은 모두 다 크고, 작은 애들은 모두 다 작음)
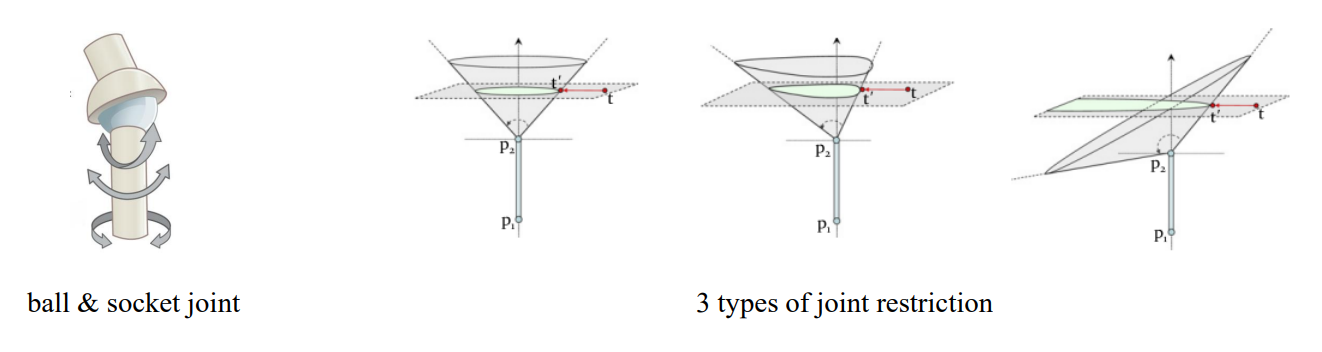
3D의 problem을 2D로 내리는 좋은 방법 중 하나가 “단면을 자르는 것”임. → target으로부터 가장 가까운 곳으로 향하는 벡터를 기준으로 자름.
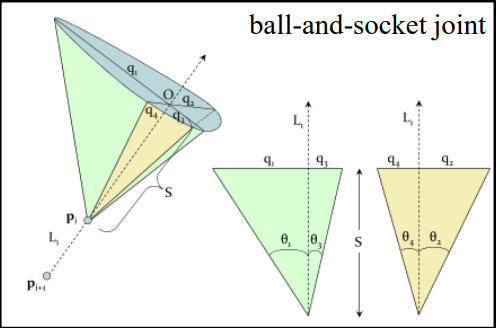
- joint limit가 타원 형태라고 가정함. (대부분 타원 형태를 띠기 때문) → 하지만 다른 종류의 conic section에도 비슷하게 적용됨.
- 이를 그림으로 표현하면:
- : 와 원점 사이의 길이
- 단면을 잘라서 3D→2D mapping을 수행하면 다음과 같음.
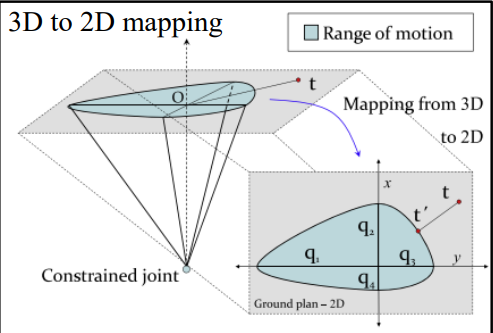
- 알고리즘의 첫 번째 스테이지 (end effector → root)를 수행 중이라고 가정. 새로운 position 을 결정했고, 번째 joint인 을 결정하려고 함.
- 과 사이의 회전을 나타내는 rotor을 찾고, 만약 이 rotor가 limit보다 큰 경우 을 limt 내로 옮김.
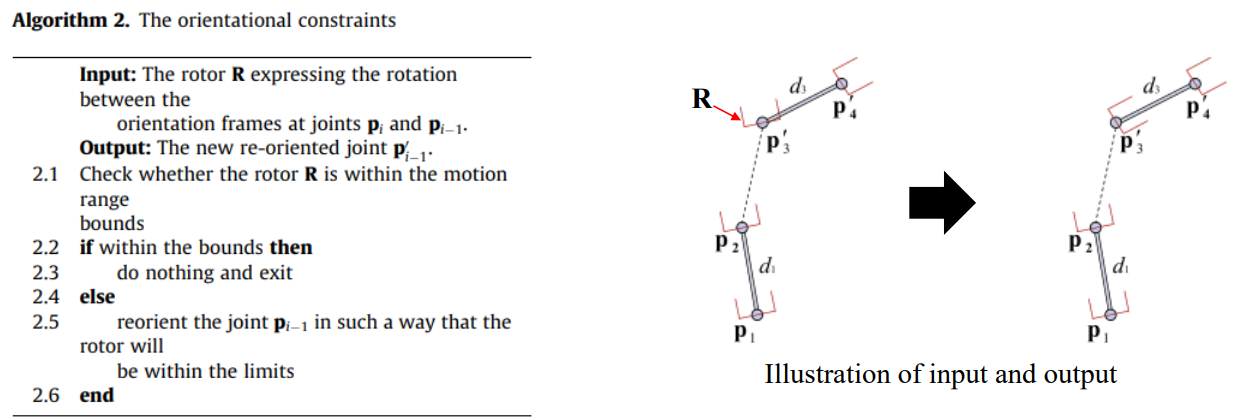
joint orientation이 결정되면, rotational limit 는 다음과 같이 적용됨.
- 와 을 잇는 직선 위로 target 의 projection 를 찾는다.
- 와 사이의 길이 를 결정하고, 길이 를 구한다. (
- 의 rotation과 translation을 적용한다. 2D 평면 상에서 target과 구동 범위가 표현되므로 가장 가까운 구동 범위를 찾아 이동시킬 수 있다.
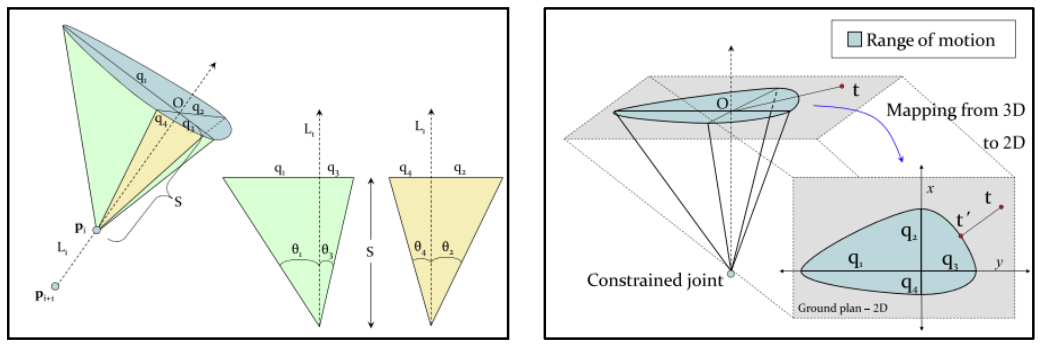
- target이 가동 범위 내에 없으면, 가장 가까운 점을 찾는다.
- 모든 사분면을 고려할 필요 없이 target이 위치한 사분면에 있는 부분만 고려한다.
- 마지막으로, 2D 평면으로 이동할 때 사용했던 행렬의 inverse를 적용하여 3D 공간 상의 위치를 결정한다.

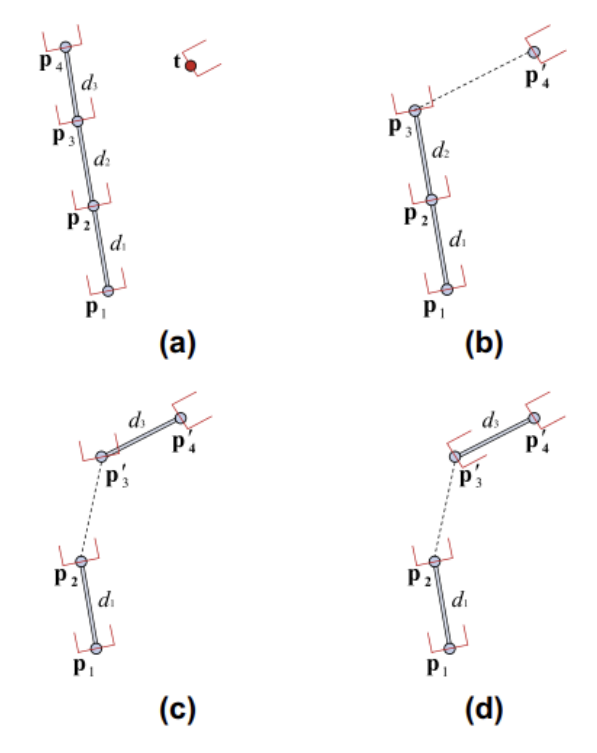
(a) 초기 상태
(b) 를 target 위치로 옮긴다. (
(c) 를 옮긴다. (하던대로.
(d) 의 orientation을 바꿔준다. (과 의 범위 내에 있는 rotor로)
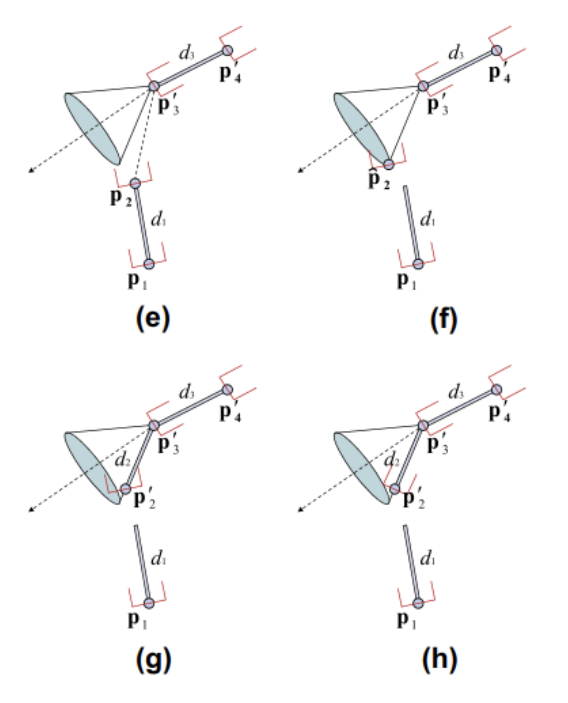
(e) rotational constraint를 적용한다. → 타원체라고 가정
(f) 를 옮기되, 의 가동 범위 내로 옮긴다. → 와 를 잇는 직선과 수직이면서 가장 가까운 곳으로 →
(g) 길이 를 맞추기 위해 의 위치를 조정한다.
(h) 와의 직선에 맞게 re-orientation한다.
⇒ re-positioning과 re-orientationing이 함께 들어가는 알고리즘
FABRIK은 이전에 사용하던 IK method보다 부드럽고 자연스러운 movement를 보여줌.
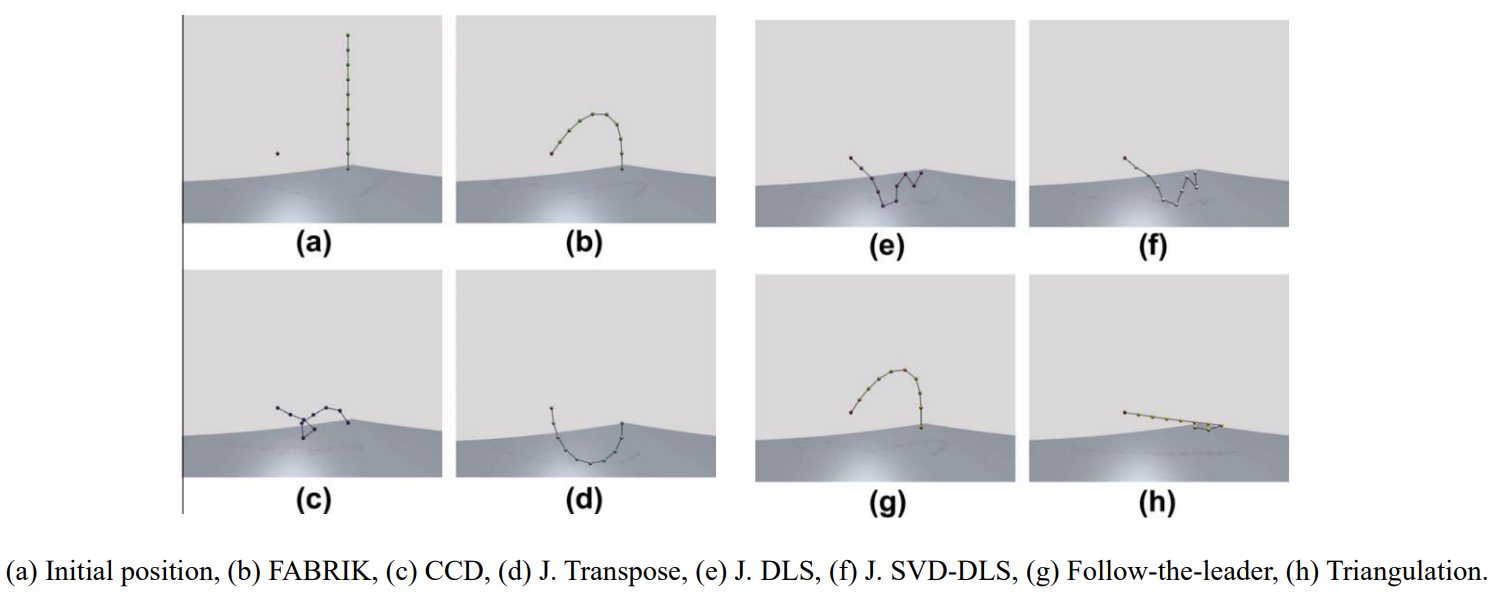
CCD는 글로벌 호구 → 아 얘보다는 확실히 좋다! (흠씬 두드려 맞는중)
<FABRIK의 성능>
- CCD보다 10배 빠름. Jacobian 기반 method보다 1,000배 빠름.
- computational cost가 적음과 동시에 시각적으로 부드럽고 자연적인 movement를 만들어낼 수 있음. (논문 저자 왈)
- iteration을 적게 수행하며, desired position에 빠르게 수렴하고, target이 unreachable일 때에도 최대한 target에 가까이 다가가는 모습을 보여줌.
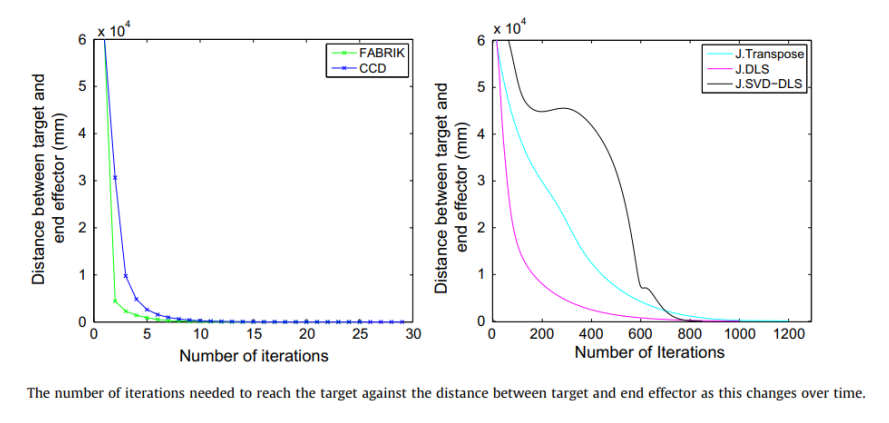
5. More Advanced Methods
FABRIK의 문제점을 개선하는 방향으로 많은 연구가 이루어지고 있음.
- Warm start for FABRIK
- Collision-free FABRIK : 중간 장애물을 고려함
- Data-driven FABRIK
- Deep learning FABRIK
Reference
[1] https://en.wikipedia.org/wiki/Definite_matrix
[2] R. M¨uller-Cajar and R. Mukundan. Triangulation: A new algorithm for inverse kinematics. In Proceedings of
the Image and Vision Computing New Zealand 2007, pages 181–186, New Zealand, December 2007.
[3] Luis Unzueta, Manuel Peinado, Ronan Boulic, and Angel Suescun. Full-body performance animation with
sequential inverse kinematics. Graph. Models, 70(5):87–104, 2008.
[4] Andreas Aristidou and Joan Lasenby. FABRIK: a fast, iterative solver for the inverse kinematics problem.
Submitted to Graphical Models, 2010.
