
1. Introduction
1-1. Quasi-Newton Methods
Newton method를 사용하면 singularity problem 없이 값을 근사하여 joint angle을 찾을 수 있지만, Hessian matrix의 inverse를 구할 때의 오버헤드가 너무 크다는 단점이 있음.
따라서 Quasi-Newton Method를 사용하여 Hessian matrix를 approximate함. (정확한 값을 구하는 것은 cost가 많이 들지만, 값을 근사하는 것은 비교적 cost가 적음.)
Quasi-Newton method에서는 함수가 0이 되는 점을 찾거나, local maxima를 찾음.
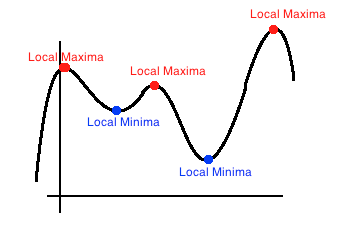
Jacobian이나 Hessian을 구할 수 없는 상황, 혹은 매 iteration의 계산량이 너무 많은 경우 대안책으로 사용할 수 있음. (근데 사실 대부분의 상황에서 Quasi-Newton을 씀)
<Quasi-Newton method의 장단점 (Newton method에 비해)>
- 장점 : computation time이 빠름.
- 단점 : 값의 정확성이 비교적 낮기 때문에, convergence (수렴)하는 속도가 느림.
<Newton method vs Quasi-Newton method>
<Newton method>
- computationally expensive
- 매 iteration마다 Hessian을 계산해야 하기 때문에 2차 미분이 필요함.
- linear system of equation을 매 iteration마다 풀어야 함.
- step을 조금만 거쳐도 수렴하는 값을 찾을 수 있음. (Quasi-Newton method에 비해)
- 비교적 정확함.
<Quasi-Newtion method>
- computationally cheap (Newton method에 비해)
- 2차 미분이 필요하지 않음.
- linear system of equation을 풀 필요가 없음.
- 비교적 많은 step이 필요함.
- 비교적 덜 정확함.
2. Basics
2-1. Definite Matrix [1]
를 의 transpose, 를 의 conjugate, 을 차원 zero vector라고 가정.
- 의 모든 에 대해, 대칭 실수 행렬 이 ⭐positive-definite⭐라는 말은 이라는 것을 의미함.
- 반면, 일 때에는 positive-semidefinite 또는 non-negative-definite라고 함.
- → negative-definite (별로 중요하지 않음)
- → negative-semidefinite 또는 non-positive-definite
positive-definite와 positive-semidefinite를 만족하면 convex 형태가 보장됨. → 특정 값으로 수렴하는 것이 확실함.
positive-definite가 보장되면 Quasi-Newton method를 사용할 수 있음.
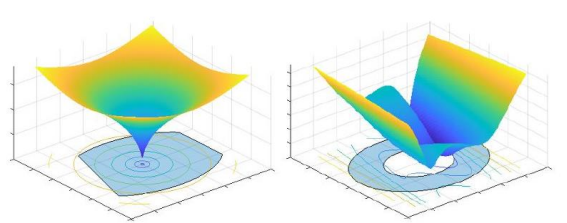
왼쪽 : convex한 형태, 오른쪽 : convex하지 않은 형태. 수렴 불가능
점 근처에서 함수가 convex하면, Hessian matrix는 에서 positive-semidefinite임.
2-2. Secant Method [2]
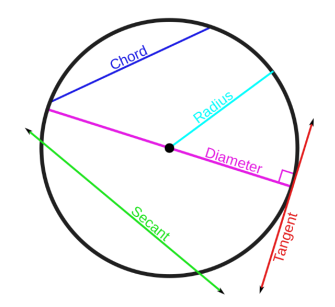
secant : 할선
원에서 secant의 특징을 본따 Secant Method라는 이름이 붙었음.
Secant method는 함수 의 root (함수가 0이 되는 지점)를 더욱 잘 근사하기 위한 root-finding algorithm. (Newton method랑 비슷함)
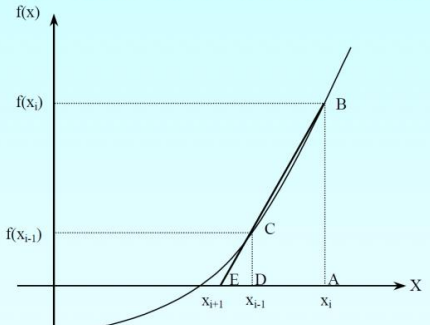
곡선 위의 두 점을 잇는 직선이 x축과 만나는 지점을 찾고, 그 점을 올려서 다시 직선을 만들고, …을 반복함.
<식 유도 과정>
위 그림에서 삼각형의 닮음 법칙을 이용함.
각 선분에 해당하는 식을 대입.
→
구하고자 하는 점은 이므로 우변으로 넘기면
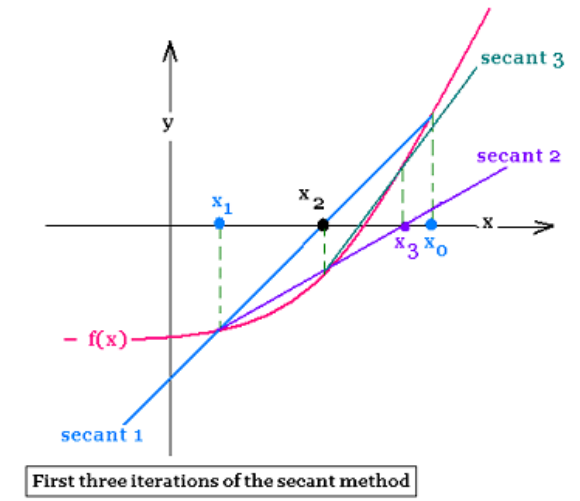
로 iteration을 돌면서 점점 root에 가까워지는 것을 볼 수 있음.
Practice
Q. Secant Method를 사용하여 방정식 의 root를 찾는다고 가정하자. 이다.
Q1. 를 계산하라.
Q2. root를 찾아라. (threshold = 0.001)
A.

3. Quasi-Newton Method
3-1. Search for extrema (optimization problem) [4]
scalar-valued function의 minimum 또는 maximum을 찾는 것은 그 함수의 gradient가 0이 되는 점을 찾는 것과 같음.
즉, 함수 의 gradient를 라고 할 때, 가 0이 되는 점을 찾는 것은 의 extrema를 찾는 것과 같음.
이때 이기 때문에 앞에서 배운 것처럼 의 Jacobian은 의 Hessian임. ()
Newton method에서는 함수가 부분적으로는 quadratic으로 근사될 수 있다고 가정하며, 1, 2차 미분을 통해 stationary point를 찾음.
또한 Newton method에서는 gradient와 Hessian을 사용하여 함수의 minimized 점을 찾았음.
반대로 Quasi-Newton method에서는 “Hessian matrix를 계산하지 않음!”
그 대신 연속적인 gradient 벡터로 Hessian을 업데이트함.
Newton method에서는 다음과 같이 업데이트를 진행했음.
그런데 각 step마다 Hessian matrix를 계산해야 하는 것은 물론 inverse까지 구해야 하기 때문에 오버헤드가 매우 큼.
따라서 Quasi-Newton method에서는 Hessian을 직접 구하지 않고, positive-definite matrix 로 approximate하는데, 이전 step에서의 정보를 통해 iterative하게 업데이트함.
이전 step의 결과를 그대로 다음 step의 input으로 사용하기 때문에 computational cost가 감소함.
행렬 의 update scheme은 어떤 종류의 Quasi-Newton method를 쓰는지에 따라 달라짐. (여러 종류의 method가 있는데, BFGS가 일반적이므로 BFGS를 예로 들 것.)
Quasi-Newton method의 종류에 상관없이 공통으로 만족해야 하는 조건이 있는데, 이를 Quasi-Newton condition (또는 secant equation)이라고 함.
→ Hessian은 2차 미분의 형태인데, 2차 미분을 직접 하지 않고, “1차 미분, 즉 gradient의 변화량”을 통해 2차 미분을 numerical하게 approximate하는 것! ()
현재 step의 정보를 모두 갖고 있으므로 다음 step의 approximation이 가능함.
다시 쓰면,
→ ⭐⭐
gradient가 0이 되어야 하므로, 은 최종적으로 다음과 같이 전개됨.
secant equation을 만족하기 위해 새로운 조건이 추가됨. → 는 대칭 행렬이어야 하며, Hessian과 최대한 가까워야 함.
3-2. Quasi-Newton steps [6]
- 을 푼다.
- step size (또는 learning rate) 을 정한다. (step size가 크면 속도는 빠르지만 정확도가 떨어지고, 작으면 정확한 대신 속도가 느림)
- 을 업데이트한다. → 다음 프레임의 를 구함.
- 으로부터 을 계산한다. → 어떤 종류의 Quasi-Newton method를 사용하는지에 따라 달라짐.
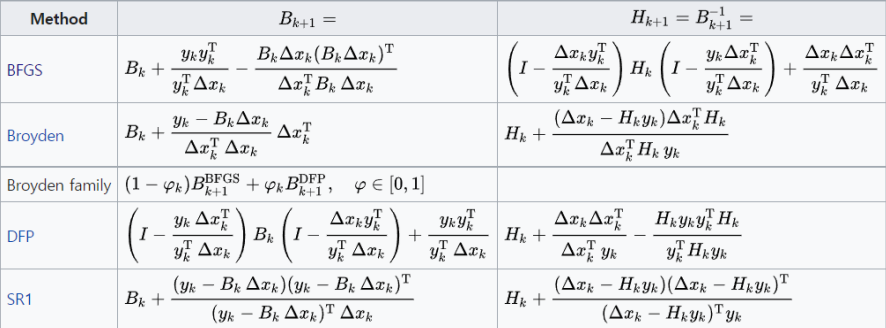
실전에서는 파이썬 코드를 통해 을 구함.
4. Broyden-Fletcher-Goldfarb-Shanno Method
4-1. Broyden-Fletcher-Goldfarb-Shanno (BFGS) Method [7]
BFGS 업데이트는 다음과 같은 형태를 가짐.
()
inverse update는 다음과 같음.
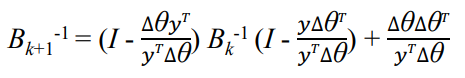
BFGS의 업데이트 & inverse update의 시간 복잡도는 → Newton method의 시간 복잡도가 이므로 오버헤드가 매우 많이 줄어들었음.
만약 이면 는 업데이트를 진행하면서 positive definite를 유지하게 되고, 결과적으로 Quasi Newton을 수행해도 특정 값에 계속 수렴할 수 있는 상태가 됨.
즉, 가 descent direction으로 간다는 것을 의미하며, 이는 극솟점을 잘 찾아서 이동하고 있다는 의미.
positive definite가 성립함을 보이기 위해 임을 증명하고, 이 때문에 를 양변에 곱해줌.
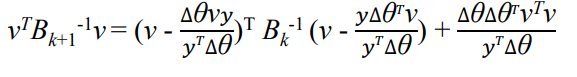
이때 이라는 것이 보장되면 모든 에 대해 위 식이 non-negative라는 것이 보장되고, 따라서 positive-definite 조건이 풀리지 않게 되면서 convex한 함수를 따라 수렴하는 상태가 됨.
BFGS는 secant condition을 만족함.
()
Secant method는 Newton method와 매우 유사하며, 따라서 2차 미분을 할 필요 없이 1차 미분 를 approximate하는 것만으로도 finite differencint을 구할 수 있음. [8]
이를 다시 쓰면 secant method와 매우 유사한 형태가 됨.
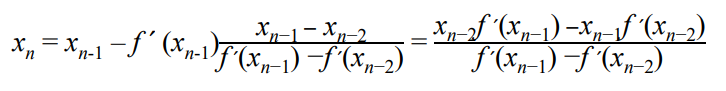
Reference
[1] https://en.wikipedia.org/wiki/Definite_matrix
[2] https://en.wikipedia.org/wiki/Secant_method
[4] https://en.wikipedia.org/wiki/Quasi-Newton_method
[6] https://www.stat.cmu.edu/~ryantibs/convexopt-F18/lectures/quasi-newton.pdf
[7] Practical Methods of Optimization, Fletcher, Roger, 1987
[8] http://www.princeton.edu/~aaa/Public/Teaching/ORF363_COS323/F14/ORF363_COS323_F14_Lec7.pdf
