캐글 스터디 발표를 위해 준비하던 중... 이것도 기록으로 남겨야겠다 싶어서 올린다.

중요 키워드

• Stationarity (정상성)
• Autocorrelation (자기상관)

Autocorrelation(자기상관)

간단하게 말해서, 본 데이터간의 상관관계를 뜻한다.
시계열 데이터로 분석 / 예측을 진행할 때, 데이터가 계절성과 추세를 띄지 않도록 해야 시간에 구애받지 않고 나은 예측을 진행할 수 있다.

좋은 예시가 있따..

현재 시간을 t라고 가정하자. t-10~t-1 시간 동안의 데이터를 학습한 모델을 t+1~t+10의 시간 동안의 데이터에 적용할 수 있을까?

답은 NO이다. 정상적이지 않은 데이터는 측정 시간에 구애받는, 즉 시간 의존성을 띈다.
그러므로 시계열 데이터는 stationartiy(정상성)를 띄어야 한다.

하지만 그렇지 못한 데이터가 많다..
그럼 이런 데이터를 어떻게 찾아낼까?
.
.

비정상적 데이터는 자기상관함수(ACF)에서의 값이 높게 측정된다.

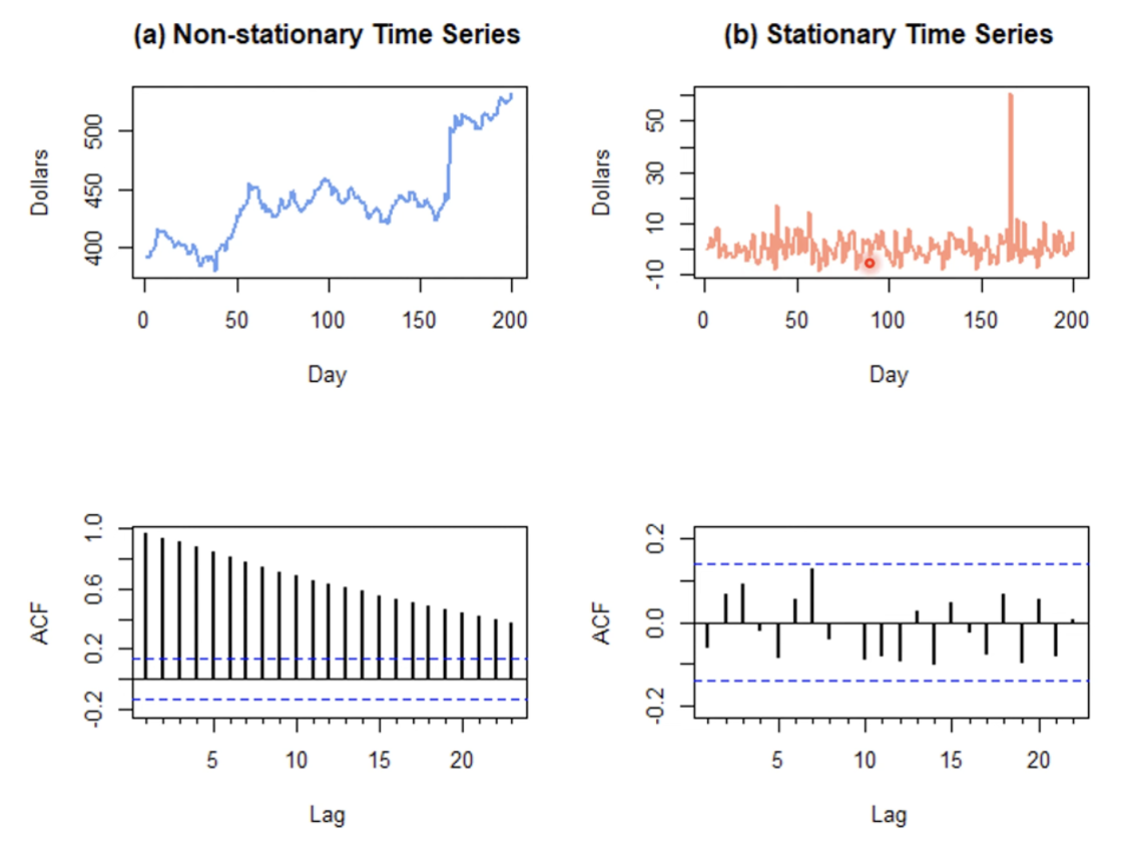
(a) 그래프는 비정상적, (b)그래프는 정상적 데이터이다.
ACF행의 그래프를 볼 경우, 자기상관함수에서의 값이 높게 측정되는 (a)와는 다르게 (b)에서는 모두 0에 가까운 것을 알 수 있다.

자기상관에서 중요한 개념이 있다. 바로 시차(lag)이다!
ACF 그래프를 보면 X축에 Lag 글자가 있는 것을 볼 수 있다.
이러한 시차와의 상관관계 정도를 자기상관이라고 하는데, 동일한 데이터를 하루 씩 밀어서 원본 데이터와 이것과의 상관관계를 체크한다.

Lag_1은 하루의 시차, Lag_2 . . Lag_N을 N일의 시차라고 가정하면,
N이 커져갈수록 Autocorrelation은 감소한다. (더욱 관련이 없어지므로)

위의 그래프를 작성하는 코드는 다음과 같다.

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

(acf그래프와 pacf그래프를 통해 확인할 수 있다.)

이렇게 확인한 자기상관성을 없애야 뛰어난 시계열 모델을 작성할 수 있음!
이를 없애기 위해서는 추세, 계절성 등의 평균과 분산의 변동을 발생시키는 요인을 제거해야 한다.
(kaggle-learn에서는 detrending, deseasoning이라고 함 + differencing(차분)이라는 것이 있음)

이 제거 방법 중 가장 유명한 것으로, ARIMA model이 있다!

ARIMA MODEL

ARIMA FORECASTING MODEL
(AutoRegressive Integrated Moving Average)

AutoRegressive : 과거 관측값의 선형 결합으로 미래 예측

Moving Average : 예측 오차를 이용하여 미래의 값 예측

파이썬에서 이를 사용하기 위해서는 다음 코드를 사용하면 된다.

from statsmodels.tsa.arima_model import ARIMA

class statsmodels.tsa.arima.model.ARIMA(
	endog, 
    exog=None, 
    order=(0, 0, 0), 
    seasonal_order=(0, 0, 0, 0), 
    trend=None, 
    enforce_stationarity=True, 
    enforce_invertibility=True, 
    concentrate_scale=False, 
    trend_offset=1, 
    dates=None, 
    freq=None, 
    missing='none', validate_specification=True)

Parameters

endog : array_like, optional

• 관측된 시계열 프로세스 y

exog : array_like, optional

• 외부 회귀 배열

order : tuple, optional

• autoregressive, differences, moving average 구성 요소에 대한 모델의 (p, d, q) order.
  d는 항상 정수이며 p와 q는 정수 또는 정수의 list일 수 있음

seasonal_order : tuple, optional

• AR parameters, differences, MA parameters, 주기성에대한 모델의 seasonal components의 (P, D, Q, s) 순서이다. 기본값은 (0, 0, 0, 0)이다. D와 s는 항상 정수인 반면 P와 Q는 정수이거나 양의 정수 list일 수 있음

trend : str{'n', 'c', 't', 'ct'} or iterable, optional

• Determinisitic trend를 제어하는 parameter. 문자열로 지정할 수 있으며 'c'는 상수 항을 나타내고 't'는 시간의 linear trend를 나타내며 'ct'는 두 가지 모두를 포함한다. 다항식을 정의하는 iterable로 지정할 수 있다.
  또한 [1,1,0,1]은 a+bt+ct^3을 나타내는numpy.poly1d와 같이 다항식을 정의하는 iterable로 지정할 수도 있다.
  기본값은 integration이 없는 모델의 경우 'c'이며 있는 모델의 경우 trend가 없다.
  모든 trend terms는 모델에 exogenous regressor 변수로 포함되며, 이는 SARIMAX 모델에 추세가 포함되는 방식과는 다르다.

enforce_stationarity : bool, optional

• autoregressive paramter가 stationarity process와 일치하도록 요구할지에 대한 여부 (T/F)

enforce_invertibility : bool, optional

• moving average parameter가 반전 가능한 프로세스에 대응할지에 대한 여부

concentrate_scale : bool, optional

• 가능성 중 scale(오차 항의 분산)을 집중시킬지 여부. 이렇게 하면 매개변수 수가 하나 줄어듦
  이는 수치적 최대 확률에 의한 추정을 고려할 때만 적용

trend_offset : int, optional

• 시간 trend 값을 시작할 오프셋. 기본값은 1이므로 trend='t'인 경우 trend는 1, 2, ..., nobs와 같음
  일반적으로 이전 데이터 집합을 확장하여 모델을 만들 때만 설정

dates : array_like of datetime, optional

• endog or exog로 인덱스가 제공되지 않으면 날짜/시간 객체의 배열과 같은 객체를 제공

freq : str, optional

• endog or exog로 인덱스가 지정되지 않은 경우, 시계열의 빈도는 여기에 Pandas 오프셋 또는 오프셋 문자열로 지정할 수 있음

missing : str

• 사용 가능한 옵션은 none, drop, raise.
  none일 경우 결측값 검사 수행 X
  drop일 경우 결측값이 있는 모든 관측값 삭제
  raise일 경우 에러가 발생
  기본값은 none

이 외에도

statsmodel 라이브러리에는 시계열을 다루기 위한 유용한 메쏘드들이 정말 많으므로 알아보며 공부하는 것이 좋을 것 같다.
참고하면 좋을 ARIMA 자료