Apply ML to forecasting task with these four strategies.
Introduction
1강과 2강에서는 시간 인덱스라는 단일 입력에서 모든 feature를 도출하는 간단한 regression 문제로 예측을 다루었다. 원하는 Trend와 Seasonal feature를 생성하기만 하면 미래의 모든 시간에 대한 예측을 쉽게 만들 수 있다.
하지만 3강에서 Lag feature를 추가하면서 문제의 성격이 달라졌다.
Lag feature를 사용하려면 예측 시점에서 지연된 목표 값을 알고 있어야 한다. Lag 1 feature는 시계열을 1단계 앞으로 이동시키므로 미래 1단계는 예측할 수 있지만 2단계는 예측할 수 없음
3강에서는 예측하려는 기간까지 항상 Lag을 생성할 수 있다고 가정했다. (즉, 모든 예측은 한 단계 앞으로만 예측). 실제 예측에서는 일반적으로 이보다 더 많은 것이 필요하므로 이번 단원에서는 다양한 상황에 대한 예측을 수행하는 방법을 알아보자.
Defining the Forecast Task
예측 모델을 설계하기 전에 설정해야 할 두 가지 사항이 있다.
- 예측이 이루어지는 시점에 어떤 정보를 사용할 수 있는지(feature), 그리고
- 예측 값이 필요한 기간(target)
예측 시작 시점(forecast origin)은 예측을 수행하는 시간이다. 실제로 예측 원점은 예측되는 시간에 대한 학습 데이터가 있는 마지막 시간이라고 생각할 수 있다. 원점까지의 모든 데이터를 사용하여 feature를 만들 수 있다.
예측 기간(forecast horizon)은 예측을 하는 시간이다. 예를 들어 '1단계' 예측 또는 '5단계' 예측과 같이 예측 기간에 포함된 time step의 수로 예측을 설명하는 경우가 많다. 예측 기간은 target을 설명한다.
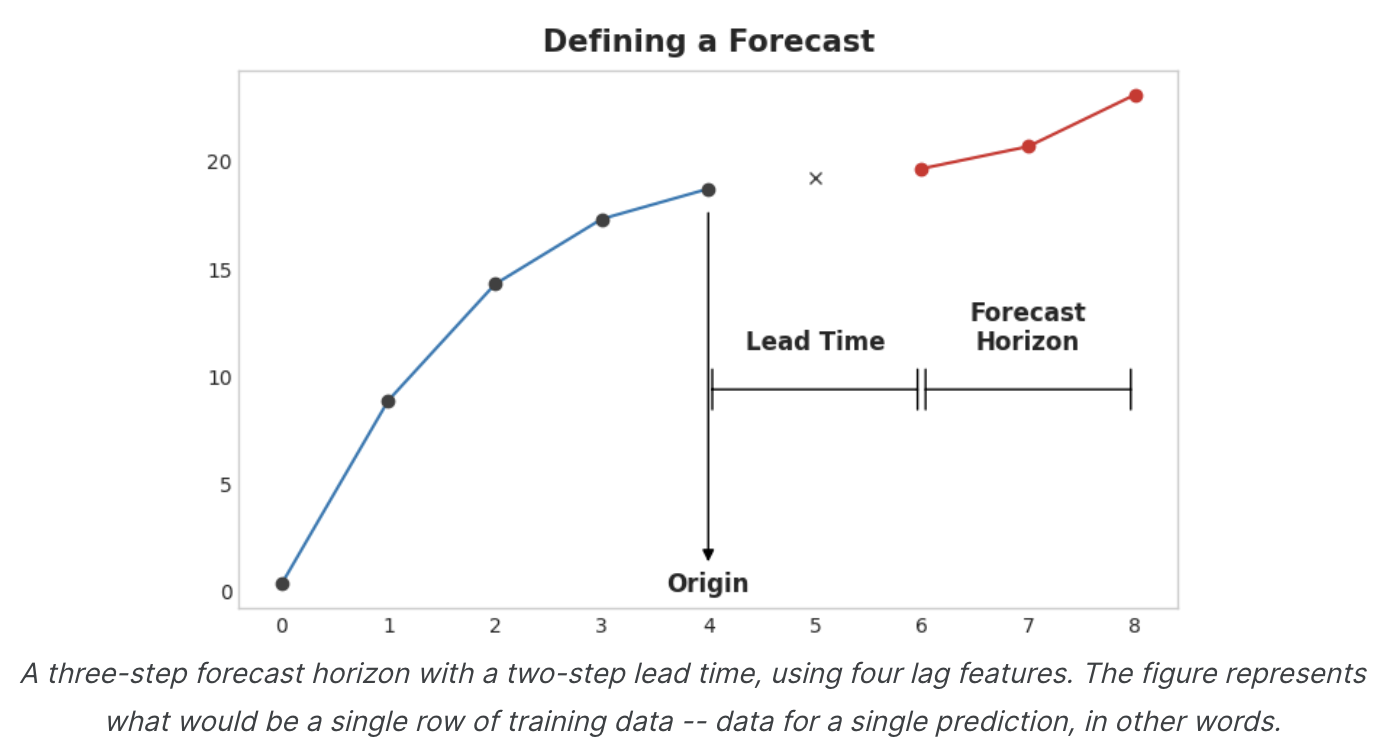
origin 과 horizon 사이의 시간을 lead time(sometimes latency) of the forecast, 예측의 리드타임(또는 대기 시간)이라고 한다.
예측의 리드 타임은 origin부터 horizon까지의 단계 수로 설명된다(예: "1단계 앞선" 또는 "2단계 앞선"). 실제로는 데이터 수집 또는 처리 지연으로 인해 예측이 origin보다 여러 단계 앞서 시작해야 할 수도 있다.
Preparing Data for Forecasting
ML 알고리즘으로 시계열을 예측하려면 해당 알고리즘에 사용할 수 있는 데이터 프레임으로 시계열을 반환해야 한다. (물론 Trend 및 Seasonality와 같은 deterministic feature만 사용하는 경우는 예외)
이 과정의 전반부는 3강에서 lag으로 feature set을 만들 때 살펴보았따. 후반부는 목표를 준비하는 단계이다. 이 작업을 수행하는 방법은 예측 작업에 따라 다르다.
데이터 프레임의 각 행은 하나의 예측을 나타낸다. 행의 시간 인덱스는 예측 기간의 첫 번째 시간이지만 전체 기간에 대한 값을 같은 행에 정렬한다. 다단계 예측(multistep forecasts)의 경우, 이는 각 단계마다 하나씩 여러 개의 출력을 생성하는 모델이 필요하다는 것을 의미한다.
import numpy as np
import pandas as pd
N = 20
ts = pd.Series(
np.arange(N),
index=pd.period_range(start='2010', freq='A', periods=N, name='Year'),
dtype=pd.Int8Dtype,
)
# Lag features
X = pd.DataFrame({
'y_lag_2': ts.shift(2),
'y_lag_3': ts.shift(3),
'y_lag_4': ts.shift(4),
'y_lag_5': ts.shift(5),
'y_lag_6': ts.shift(6),
})
# Multistep targets
y = pd.DataFrame({
'y_step_3': ts.shift(-2),
'y_step_2': ts.shift(-1),
'y_step_1': ts,
})
data = pd.concat({'Targets': y, 'Features': X}, axis=1)
data.head(10).style.set_properties(['Targets'], **{'background-color': 'LavenderBlush'}) \
.set_properties(['Features'], **{'background-color': 'Lavender'})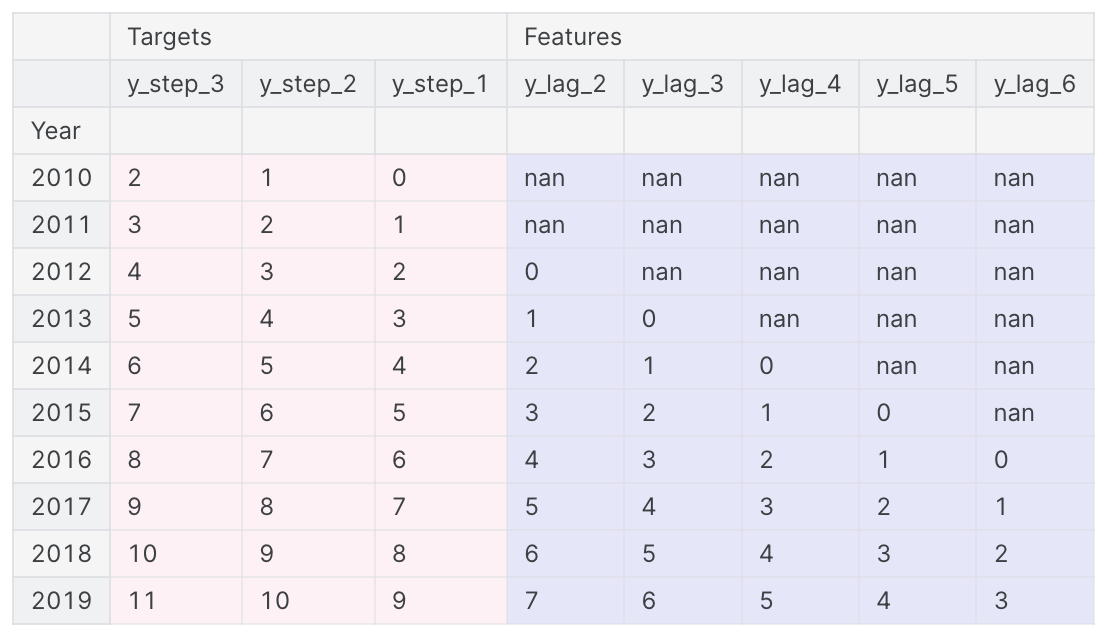
위는 예측 정의하기 그림과 유사한 데이터 집합을 준비하는 방법, 즉 5개의 Lag plot을 사용하는 2단계 lead time의 3단계 예측 작업을 보여준다. 원래 시계열은 y_step_1이다.
Multistep Forecasting Strategies
예측에 필요한 여러 목표 단계를 생성하는 데는 여러가지 전략이 있다. 각각의 장단점이 있는 네 가지 일반적 전략에 대해 알아보자.
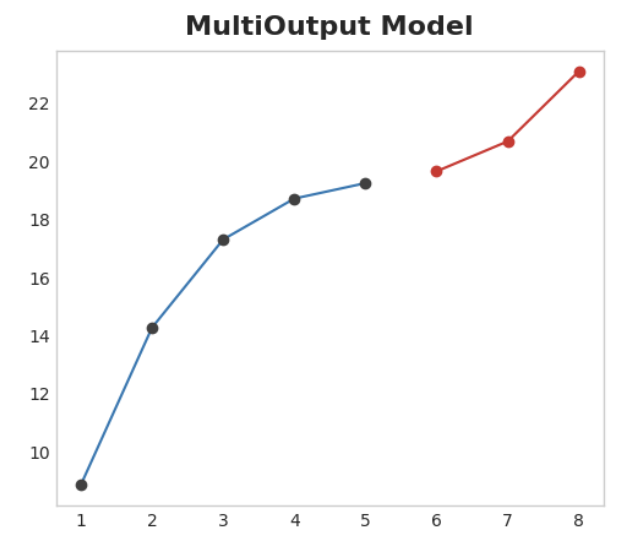
Multioutput model
여러 개의 출력을 자연스럽게 생성하는 모델을 사용하자. 선형 회귀와 신경망은 모두 여러 개의 출력을 생성할 수 있다. 이 전략은 간단하고 효율적이지만 사용하려는 모든 알고리즘에 적용할 수 있는 것은 아니다. XGBoost는 이 작업을 수행할 수 없다.
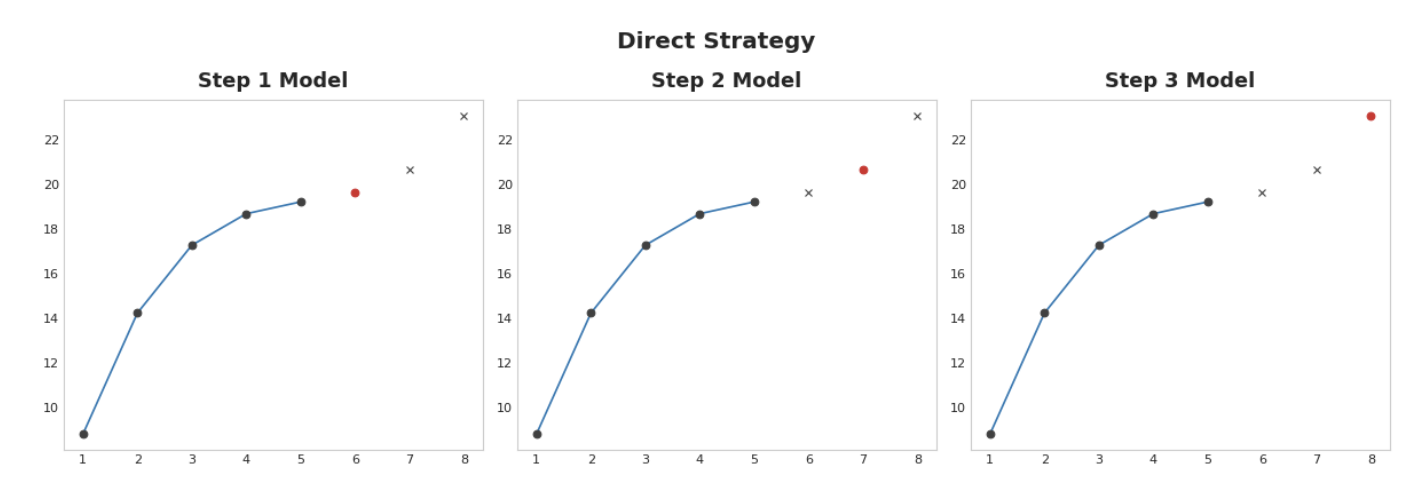
Direct strategy
한 모델은 1단계 앞을, 다른 모델은 2단계 앞을 예측하는 방식으로 각 단계마다 별도의 모델을 학습시킨다. 1단계 앞을 예측하는 것은 2단계 앞을 예측하는 것과는 다른 문제이므로 각 단계마다 다른 모델이 예측을 수행하도록 하는 것이 도움이 될 수 있다.
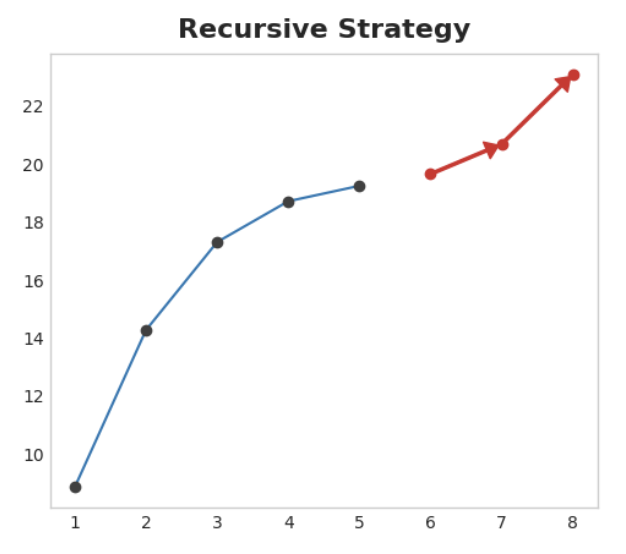
Recursive strategy
단일 1단계 모델을 학습시키고 그 예측을 사용하여 다음 단계의 lag feature를 업데이트한다. 재귀적 방법에서는 모델의 1단계 예측을 다음 예측 단계의 lag feature로 사용하기 위해 동일한 모델에 다시 입력한다. 하나의 모델만 학습시키면 되지만 단계마다 오류가 전파되기 때문에 긴 기간의 예측이 부정확할 수 있다.
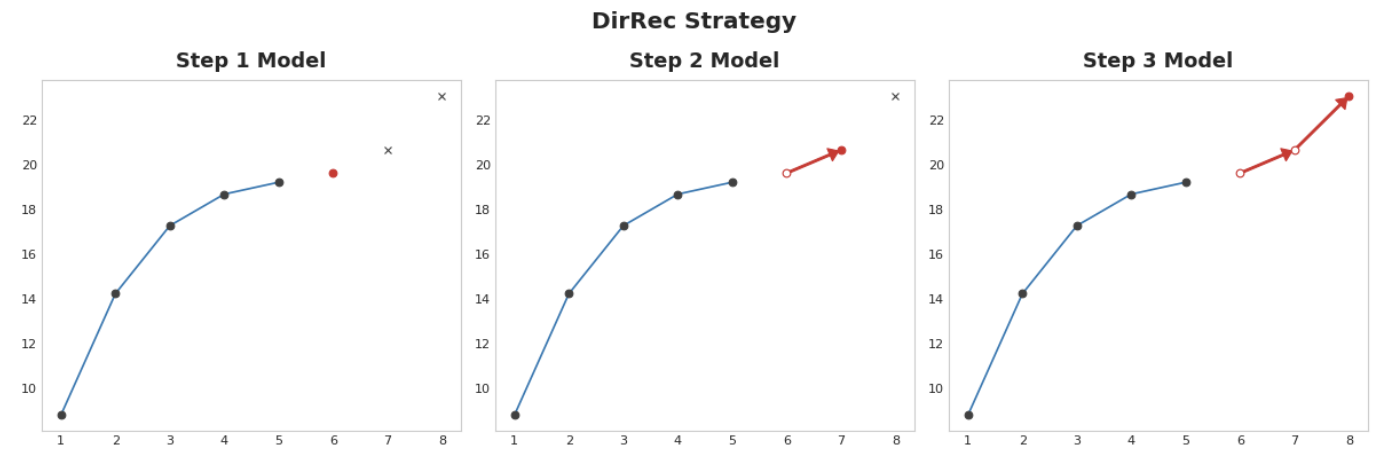
DirRec strategy
직접 및 재귀는 각 단계별로 모델을 학습시키고 이전 단계의 예측을 새로운 lag feature로 사용한다. 단계별로 각 모델은 추가 lag input을 받는다. 각 모델에는 항상 최신 lag feature set이 있기 때문에 DirRec은 직접보다 직렬 의존성을 더 잘 포착할 수 있지만 재귀처럼 오류 전파가 발생할 수도 있다.
Example - Flu Trends
3강의 독감 동향 데이터에 multistep output 및 Direct strategy를 적용하여 여러 주에 대한 실제 예측을 해보자.
예측 작업의 기간을 8주, lead time은 1주라고 정의하자.
다음 주부터 8주 동안의 예측을 하는 것이다.
다음은 plot_multistep의 정의
from pathlib import Path
from warnings import simplefilter
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from xgboost import XGBRegressor
simplefilter("ignore")
# Set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(11, 4))
plt.rc(
"axes",
labelweight="bold",
labelsize="large",
titleweight="bold",
titlesize=16,
titlepad=10,
)
plot_params = dict(
color="0.75",
style=".-",
markeredgecolor="0.25",
markerfacecolor="0.25",
)
%config InlineBackend.figure_format = 'retina'
def plot_multistep(y, every=1, ax=None, palette_kwargs=None):
palette_kwargs_ = dict(palette='husl', n_colors=16, desat=None)
if palette_kwargs is not None:
palette_kwargs_.update(palette_kwargs)
palette = sns.color_palette(**palette_kwargs_)
if ax is None:
fig, ax = plt.subplots()
ax.set_prop_cycle(plt.cycler('color', palette))
for date, preds in y[::every].iterrows():
preds.index = pd.period_range(start=date, periods=len(preds))
preds.plot(ax=ax)
return ax
data_dir = Path("../input/ts-course-data")
flu_trends = pd.read_csv(data_dir / "flu-trends.csv")
flu_trends.set_index(
pd.PeriodIndex(flu_trends.Week, freq="W"),
inplace=True,
)
flu_trends.drop("Week", axis=1, inplace=True)먼저 multistep forecasting을 위해 target series(독감으로 인한 office 방문)를 준비한다. 이 작업이 완료되면 훈련과 예측이 간단해진다.
def make_lags(ts, lags, lead_time=1):
return pd.concat(
{
f'y_lag_{i}': ts.shift(i)
for i in range(lead_time, lags + lead_time)
},
axis=1)
# Four weeks of lag features
y = flu_trends.FluVisits.copy()
X = make_lags(y, lags=4).fillna(0.0)
def make_multistep_target(ts, steps):
return pd.concat(
{f'y_step_{i + 1}': ts.shift(-i)
for i in range(steps)},
axis=1)
# Eight-week forecast
y = make_multistep_target(y, steps=8).dropna()
# Shifting has created indexes that don't match. Only keep times for
# which we have both targets and features.
y, X = y.align(X, join='inner', axis=0)Multioutput model
multioutput strategy로 선형 회귀를 사용한다.
# Create splits
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, shuffle=False)
model = LinearRegression()
model.fit(X_train, y_train)
y_fit = pd.DataFrame(model.predict(X_train), index=X_train.index, columns=y.columns)
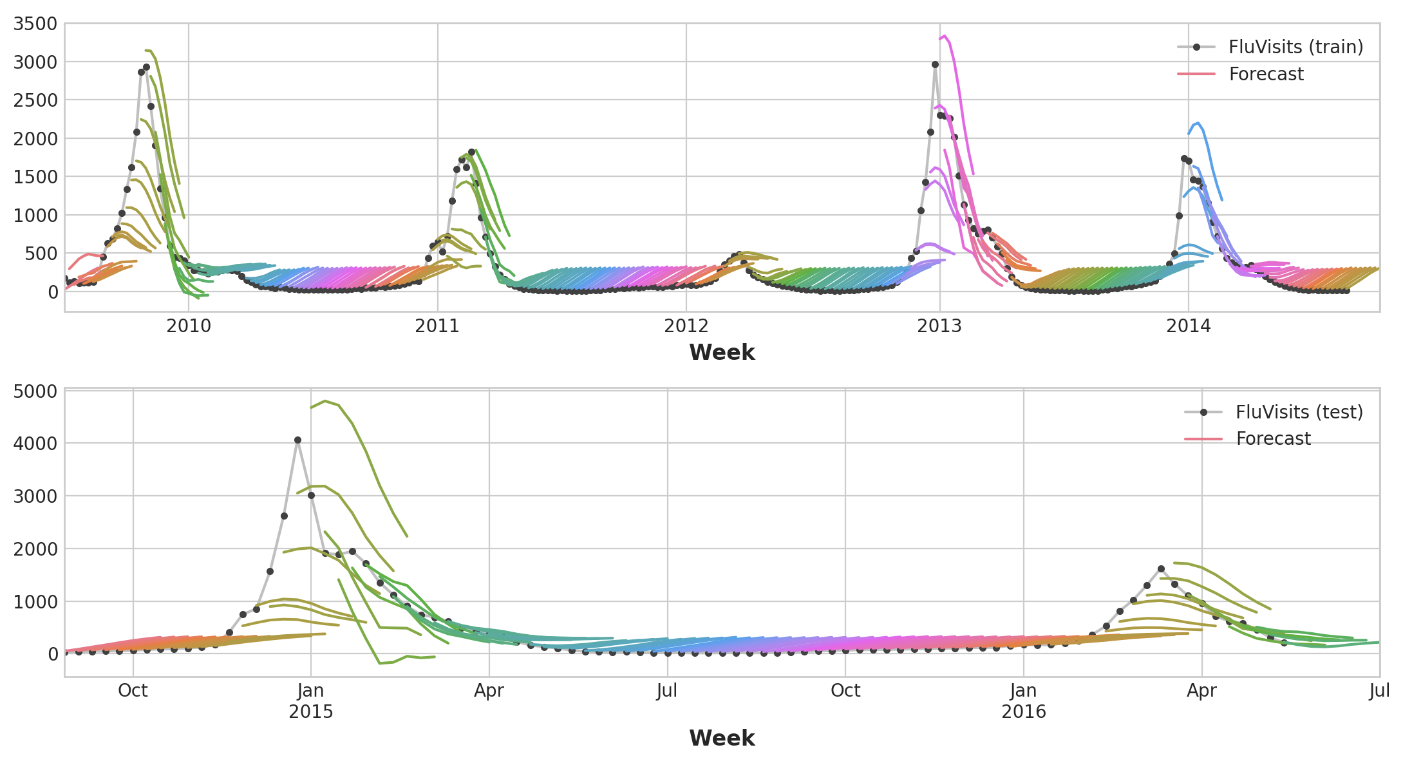
y_pred = pd.DataFrame(model.predict(X_test), index=X_test.index, columns=y.columns)multistep model은 입력으로 사용된 각 instance에 대해 완전한 예측을 생성한다.
train set에는 269주, test set에는 90주가 있으며
이제 각 주에 대한 8단계 예측이 있다.
train_rmse = mean_squared_error(y_train, y_fit, squared=False)
test_rmse = mean_squared_error(y_test, y_pred, squared=False)
print((f"Train RMSE: {train_rmse:.2f}\n" f"Test RMSE: {test_rmse:.2f}"))
palette = dict(palette='husl', n_colors=64)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(11, 6))
ax1 = flu_trends.FluVisits[y_fit.index].plot(**plot_params, ax=ax1)
ax1 = plot_multistep(y_fit, ax=ax1, palette_kwargs=palette)
_ = ax1.legend(['FluVisits (train)', 'Forecast'])
ax2 = flu_trends.FluVisits[y_pred.index].plot(**plot_params, ax=ax2)
ax2 = plot_multistep(y_pred, ax=ax2, palette_kwargs=palette)
_ = ax2.legend(['FluVisits (test)', 'Forecast'])
Direct strategy
XGBoost는 회귀 작업에 대해 여러 개의 출력을 생성할 수 없다.
하지만 Direct reduction strategy를 사용하면 multistep forecasting을 생성하는 데 여전히 사용할 수 있다.
이는 scikit-learn의 MultiOutputRegressor로 간단하게 사용할 수 있다.
from sklearn.multioutput import MultiOutputRegressor
model = MultiOutputRegressor(XGBRegressor())
model.fit(X_train, y_train)
y_fit = pd.DataFrame(model.predict(X_train), index=X_train.index, columns=y.columns)
y_pred = pd.DataFrame(model.predict(X_test), index=X_test.index, columns=y.columns)XGBoost는 train set에서 분명히 과적합하나, test set에서는 선형회귀 모델보다 독감 시즌의 역학 관계를 더 잘 포착할 수 있었던 것을 보인다. hyper parameter tuning으로 더 나은 결과를 얻을 수 있을 것이다.
train_rmse = mean_squared_error(y_train, y_fit, squared=False)
test_rmse = mean_squared_error(y_test, y_pred, squared=False)
print((f"Train RMSE: {train_rmse:.2f}\n" f"Test RMSE: {test_rmse:.2f}"))
palette = dict(palette='husl', n_colors=64)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(11, 6))
ax1 = flu_trends.FluVisits[y_fit.index].plot(**plot_params, ax=ax1)
ax1 = plot_multistep(y_fit, ax=ax1, palette_kwargs=palette)
_ = ax1.legend(['FluVisits (train)', 'Forecast'])
ax2 = flu_trends.FluVisits[y_pred.index].plot(**plot_params, ax=ax2)
ax2 = plot_multistep(y_pred, ax=ax2, palette_kwargs=palette)
_ = ax2.legend(['FluVisits (test)', 'Forecast'])

DirRec strategy를 사용하려면 MultiOutputRegressor만 다른 scikit-learn wrapper인 RegressorChain으로 대체하면 된다.
Recursion strategy는 따로 직접 코딩해야 한다.
