[백준 1932번 : 정수 삼각형] java 풀이

백준 1932번 : 정수 삼각형

이 문제는 비교적 쉽게 풀어냈다. 그림으로 설명하자면,

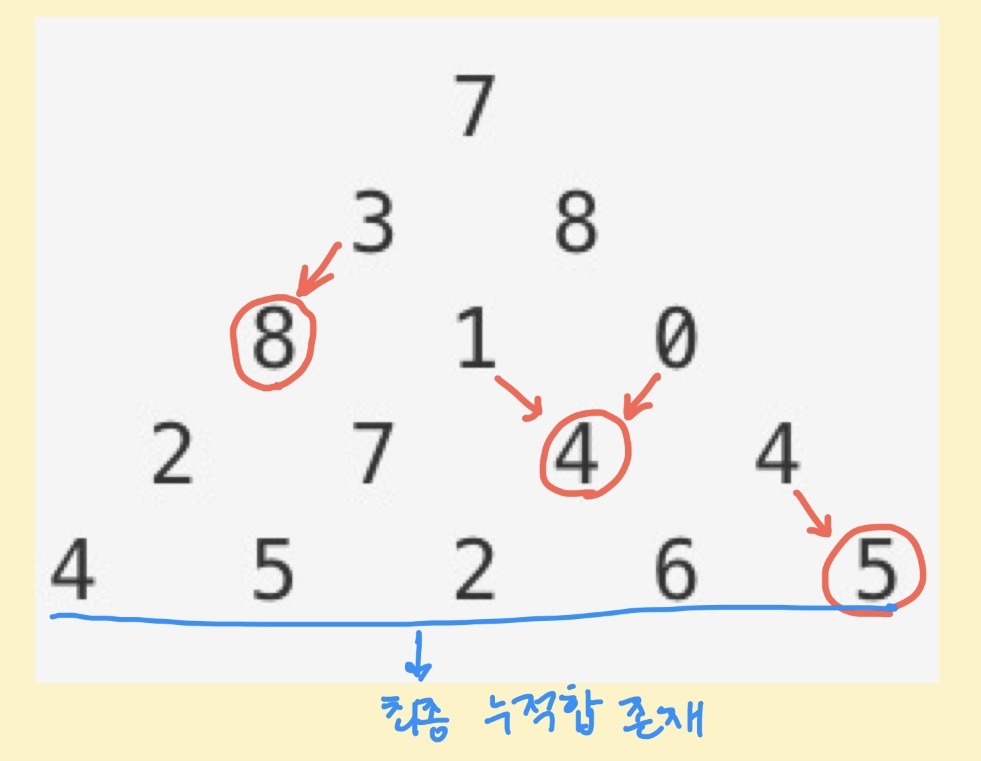
처음에는 4가 선택할 수 있는 숫자는 2와 6이므로 2와 6 중 큰 숫자를 선택하는 방향으로 생각했다.

하지만 동적계획법으로 풀 때 반대로 4가 선택받을 수 있는 숫자 1과 0 중 큰 숫자를 누적하는 방향으로 dp 점화식을 세웠다.

맨 왼쪽 또는 오른쪽에 존재하는 숫자들은 각자 대각선에 있는 숫자 하나한테만 선택받을 수 있다. 위 그림을 보면 8은 3한테만 선택받을 수 있다. 또한 5는 4한테만 선택받을 수 있다.

이외의 숫자들은 자신을 선택할 수 있는 숫자가 각자 2개씩 존재하므로 그 중 큰 값을 누적한다.

• 위와 같이 각 숫자들을 arr 배열에 담는다
• dp 배열을 생성하고 arr 배열의 첫번째 값으로 초기화한다.
• 인덱스 (j==0) 은 맨 왼쪽 숫자, 인덱스 (j==j+1)은 맨 오른쪽 숫자이다.
• 이외는 가운데 숫자들이다

따라서 점화식을 세우면

if(j==0) {
dp[i][j]=dp[i-1][j]+arr[i][j];
}
else if(j==j+i) {
dp[i][j]=dp[i-1][j-1]+arr[i][j];
}
else {
dp[i][j]=Math.max(dp[i-1][j-1], dp[i-1][j])+arr[i][j];
}

🔑java 풀이

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Scanner;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
         Scanner sc = new Scanner(System.in);
         int n = sc.nextInt();
         int arr[][] = new int[n][n];
         int dp[][]=new int[n][n];
         
         for(int i=0; i<n; i++) {
        	 for(int j=0; j<=i; j++) {
        		 arr[i][j]=sc.nextInt();
        	 }
         }
         dp[0][0]=arr[0][0];
         for(int i=1; i<n; i++) {
        	 for(int j=0; j<=i; j++) {
        		 if(j==0) {
        			 dp[i][j]=dp[i-1][j]+arr[i][j];
        		 }
        		 else if(j==j+i) {
        			 dp[i][j]=dp[i-1][j-1]+arr[i][j];
        		 }
        		 else {
        			 dp[i][j]=Math.max(dp[i-1][j-1], dp[i-1][j])+arr[i][j];
        		 } 
        	 }
         }
         int max=0;
         for(int i=0; i<n; i++) {
        	 if(max<dp[n-1][i])
        		 max=dp[n-1][i];
         }
         System.out.println(max);
    }
}