[백준 2579번 : 계단 오르기] java 풀이

백준 2579번 : 계단 오르기 바로가기

이 문제는 또 굉장히 헷갈렸다..(나 진짜 바보인가😭)

단계별 알고리즘 문제는 각 문제마다 백준에서 작은 힌트를 코멘트로 달아놓는다. 이를 확인해보면,

"i번째일 경우, 몇 개의 연속한 계단을 올랐는지 고려하라"

즉 점화식을 세울 때 규칙 중 하나였던 "세 개의 계단을 연속해서 오를 수 없다"를 고려하라는 것이다.

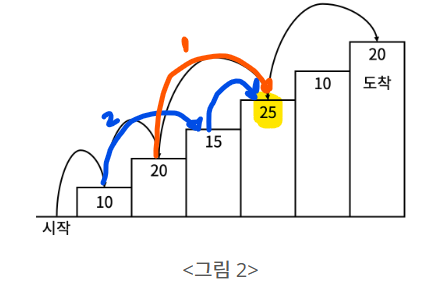
예를 들어, 점수가 25인 4번째 계단일 경우, 두 가지의 경우가 존재할 수 있다.

• 1번 화살표처럼 두 칸 뒤에서 오른 경우
• 2번 화살표처럼 연속해서 한 칸만에 오른 경우

2번 화살표의 경우는 단순히 세 번째 계단에서 한 번만 오른 경우만 고려하면 안된다. 두 번째, 세 번째, 네 번째 계단을 오르는 경우까지 포함되기 때문이다. 따라서 세 칸 뒤에서부터 두 칸을 오르고, 그 다음 한 칸을 오르는 경우로 포함시켜야 세 칸 연속 오르는 경우를 방지할 수 있다.

따라서 점화식은,
dp[n]=Math.max(sum(n-2),sum(n-3)+stair[n-1])+stair[n];

• dp 배열의 0번째 인덱스는 시작으로써 0이 들어간다.
• dp 배열의 1번째 인덱스는 첫번째 계단의 점수가 들어간다.
• 따라서 dp 배열과 stair 배열 모두 n+1 크기로 선언한다.
• dp 배열의 2번째 인덱스는 첫번째 계단의 점수와 두번 째 계단의 점수를 합한 값이 들어간다. 계단이 두 개밖에 없는 경우 두 계단의 점수를 합한 값이 최대값이기 때문이다.
• 주의사항은 n 값이 1일 경우를 고려해서 작성해야한다.

참고 블로그 : https://st-lab.tistory.com/132

🔑java 풀이

import java.io.IOException;
import java.util.Scanner;

public class Main {

    static int dp[];
    static int stair[];
    static int sum(int n){
        if(dp[n]==-1){
            dp[n]=Math.max(sum(n-2),sum(n-3)+stair[n-1])+stair[n];
        }
        return dp[n];
    }
    public static void main(String[] args) throws IOException {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        stair=new int[n+1];
        for(int i=1; i<n+1; i++){
            stair[i]=sc.nextInt();
        }

        dp=new int[n+1];
        for(int i=0; i<n+1; i++)
            dp[i]=-1;

        dp[0]=0;
        dp[1]=stair[1];
        if(n==1){
            System.out.println(dp[n]);
            return;
        }
        dp[2]=stair[1]+stair[2];

        System.out.println(sum(n));
    }
}