1. 다이나믹 프로그래밍이란?
다이나믹 프로그래밍은 큰 문제를 작은 문제로 나눠서 푸는 알고리즘을 의미한다.
Dynamic은 아무 의미가 없는 용어이고 이 용어를 1940년에 처음 사용한 Richard Bellman은 그냥 Dynamic이란 용어가 멋있어서 사용했다고 한다.
2. 언제 사용하는가?
문제가 두 가지 속성을 만족해야 다이나믹 프로그래밍으로 문제를 풀 수 있다.
(1) Overlapping Subproblem (중복된 하위 문제)
(2) Optimal Substructure (최적 부분 구조)
• Overlapping Subproblem
Overlapping Subproblem의 좋은 예시로 피보나치 수열이 있다.
F[0] = 0
F[1] = 1
F[N] = F[N-1] + F[N-2]
F[N]을 구하기 위해서는 F[N-1]과 F[N-2]를 구해야 한다.
이때 F[N]을 큰 문제, F[N-1]과 F[N-2]를 작은 문제라고 해보자.
큰 문제와 작은 문제는 상대적이다.
문제 : N번째 피보나치 구하는 문제
작은 문제 : N-1번째 피보나치 구하는 문제, N-2번째 피보나치 구하는 문제
문제 : N-1번째 피보나치 구하는 문제
작은 문제 : N-2번째 피보나치 구하는 문제, N-3번째 피보나치 구하는 문제
문제 : N-2번째 피보나치 구하는 문제
작은 문제 : N-3번째 피보나치 구하는 문제, N-4번째 피보나치 구하는 문제
큰 문제와 작은 문제를 같은 방법으로 풀 수 있어야 하고, 문제를 작은 문제로 쪼갤 수 있어야 한다.
• Optimal Substructure
Optimal Substructure의 핵심은 문제의 정답을 작은 문제의 정답에서 구할 수 있다는 것이다.
문제 : N번째 피보나치 구하는 문제
작은 문제 : N-1번째 피보나치 구하는 문제, N-2번째 피보나치 구하는 문제
문제의 정답을 작은 문제의 정답을 합한 것으로 구할 수 있다.
문제 : N-1번째 피보나치 구하는 문제
작은 문제 : N-2번째 피보나치 구하는 문제, N-3번째 피보나치 구하는 문제
문제의 정답을 작은 문제의 정답을 합한 것으로 구할 수 있다.
문제 : N-2번째 피보나치 구하는 문제
작은 문제 : N-3번째 피보나치 구하는 문제, N-4번째 피보나치 구하는 문제
문제의 정답을 작은 문제의 정답을 합한 것으로 구할 수 있다.
Optimal Substructure을 만족한다면 문제의 크기에 상관없이 어떤 한 문제의 정답은 일정하다.
10번째 피보나치 수를 구하면서 구한 4번째 피보나치 수
9번째 피보나치 수를 구하면서 구한 4번째 피보나치 수
~~
5번째 피보나치 수를 구하면서 구한 4번째 피보나치 수
4번째 피보나치 수를 구하면서 구한 4번째 피보나치 수
★ 4번째 피보나치 수는 항상 같다.
Optimal Substructure의 또 다른 예시로 서울에서 부산까지 가는 최단 경로를 생각해보자.
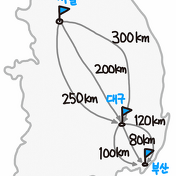
그림에서 보듯이, 서울에서 대구까지 가는 경로는 3가지, 대구에서 부산까지 가는 경우는 3가지다.
그러면 서울에서 부산까지 가는 최단 경로는 280km이다.
서울에서 대구까지의 최단 경로인 200km와 대구에서 부산까지의 최단 경로인 80km가 합쳐져 나온 값이다.
따라서 서울에서 부산까지의 최단 경로는 각각의 부분 문제인 1) 서울에서 대구까지의 최단 경로 문제 + 2) 대구에서 부산까지의 최단 경로 문제의 합으로 구할 수 있다.
이러한 구조를 최적 부분 구조라 하며, 이런 유형의 문제는 분할 정복으로 풀 수 있다. 그러나 만약 서울에서 부산까지 바로 연결되는 고속도로가 생겨 더 이상 대구를 거칠 필요가 없다면, 이 문제는 더 이상 최적 부분 구조가 아니다. 그렇다면 DP로 풀 수 없다.
3. 방법론
메모제이션(Memoization)
• 다이나믹 프로그래밍에서 각 문제는 한 번만 풀어야 한다.
• Optimal Substructure를 만족하기 때문에, 같은 문제는 구할 때마다 정답이 같다.
• 따라서, 정답을 한번 구했으면 정답을 어딘가에 메모해놓는다.
• 이런 메모하는 것을 코드의 구현에서는 배열에 저장하는 것으로 할 수 있다.
• 메모를 한다고 해서 Memoization이라고 한다.
def fibo(n):
if n<=1:
return n
else:
return fibo(n-1)+fibo(n-2)일반적인 피보나치 수열 함수
memo=[0]*100
def fibo(n):
if n<=1:
return n
else:
if memo[n]>0:
return memo[n]
memo[n] = fibo(n-1) + fibo(n-2)
return memo[n]메모제이션을 활용한 피보나치 수열 함수
4. 구현방식
다이나믹 프로그래밍의 구현방식에는 Top Down, Bottom up 두 가지 방법이 있다.
이때, Top Down방식은 메모제이션과 함께 쓰이고 Bottom Up방식은 타뷸레이션과 함께 쓰인다.
1. Top Down
(1) 큰 문제를 작은 문제로 나눈다.
(2) 작은 문제를 푼다.
(3) 작은 문제를 이용해 큰 문제를 푼다.
(1) 큰 문제를 작은 문제로 나눈다.
fibo[n] = fibo[n-1] + fibo[n-2]
(2) 작은 문제를 푼다.
fibo[n-1]과 fibo[n-2]를 구한다.
(3) 작은 문제를 이용해 큰 문제를 푼다.
fibo[n-1]과 fibo[n-2]를 더해 fibo[n]을 구한다.
Top Down은 재귀호출을 이용해 문제를 풀 수 있다.
호출 전에 메모제이션으로 이미 존재하는 값인지 확인하자.
2. Bottom Up
(1) 문제를 크기가 작은 문제부터 차례로 푼다.
(2) 문제의 크기를 조금씩 크게 만들면서 문제를 점점 푼다.
(3) 작은 문제를 풀면서 왔기 때문에, 큰 문제는 항상 풀 수 있다.
(4) 반복하다 보면 가장 큰 문제를 풀 수 있다.
memo=[0]*100
def fibo(n):
memo[0]=0
memo[1]=1
for i in range(2,n+1):
memo[i]=memo[i-1]+memo[i-2]
return memo[i]
(1) 문제를 크기가 작은 문제부터 차례로 푼다.
for i in range(2,n+1)(2) 문제의 크기를 조금씩 크게 만들면서 문제를 점점 푼다.
for i in range(2,n+1) # i가 증가함(3) 작은 문제를 풀면서 왔기 때문에, 큰 문제는 항상 풀 수 있다.
memo[i]=memo[i-1]+memo[i-2](4) 반복하다 보면 가장 큰 문제를 풀 수 있다.
return memo[i]
Bottom Up은 단순 반복문을 이용해 문제를 풀 수 있다.
5. 문제풀이 전략
• 문제에서 구하려고 하는 답을 문장으로 나타낸다.
• 예 : 피보나치 수를 구하는 문제
• N번째 피보나치 수를 구하는 문제
• 이제 그 문장에 나와있는 변수의 개수만큼 메모하는 배열을 만든다.
• Top Down인 경우에는 재귀호출의 인자의 개수
• 문제를 작은 문제로 나누고, 수식을 이용해서 풀어야 한다.
