큐(Queue)
• 한쪽 끝에서만 자료를 넣고 다른 한쪽 끝에서만 뺄 수 있는 자료구조


• 먼저 넣은 것이 가장 먼저 나오기 때문에 First In Frist Out (FIFO) 라고도 한다.
• python의 경우 queue 구현시 collections.deque를 사용하는 것이 좋다.
• push : 큐에 자료를 넣는 연산
• pop : 큐에서 자료를 빼는 연산
• front : 큐의 가장 앞에 있는 자료를 보는 연산
• back : 큐의 가장 뒤에 있는 자료를 보는 연산
• empty : 큐가 비어있는지 아닌지를 알아보는 연산
• size : 큐에 저장되어있는 자료의 개수를 알아보는 연산
덱(Deque)
• 양 끝에서만 자료를 넣고 양 끝에서 뺄 수 있는 자료구조
• Double-ended queue의 약자이다.
• push_front : 덱의 앞에 자료를 넣는 연산
• push_back : 덱의 뒤에 자료를 넣는 연산
• pop_front : 덱의 앞에서 자료를 빼는 연산
• pop_back : 덱의 두에서 자료를 빼는 연산
• front : 덱의 가장 앞에 있는 자료를 보는 연산
• back : 덱의 가장 뒤에 있는 자료를 보는 연산
그래프(Graph)
• 자료구조의 일종
• 정점 (Node, Vertex) • 간선 (Edge): 정점간의 관계를 나타낸다.
• G = (V, E)로 나타낸다.
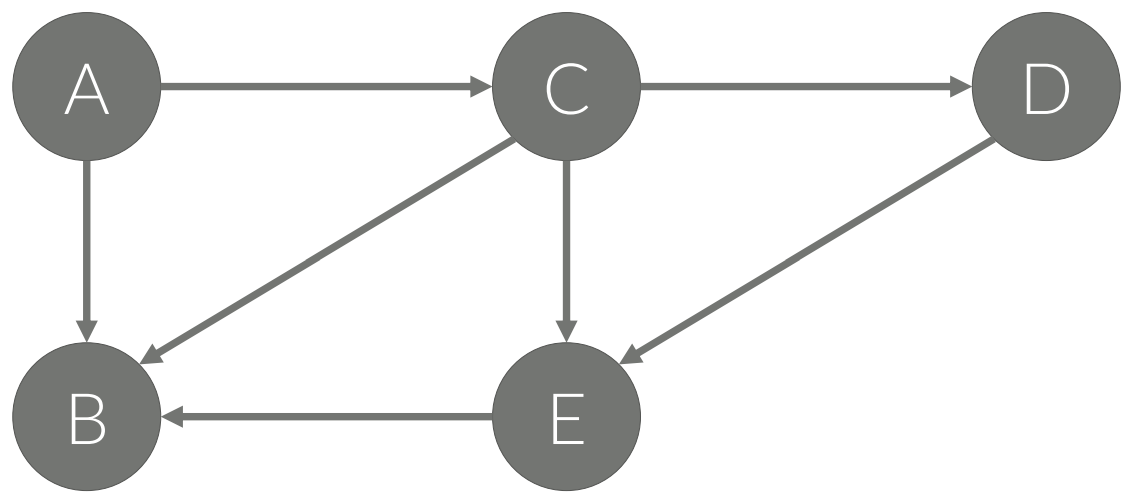
경로(Path)
• 정점 A에서 B로 가는 경로
• A → C → D → E → B
• A → B
• A → C → B
• A → C → E → B
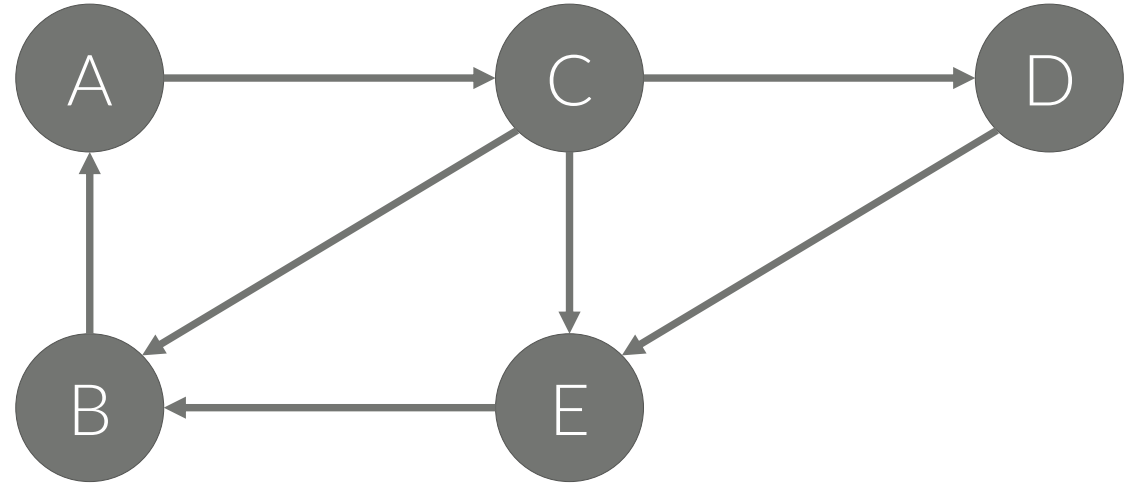
사이클(Cycle)
• 정점 A에서 다시 A로 돌아오는 경로
• A → C → B → A
• A → C → E → B → A
• A → C → D → E → B → A
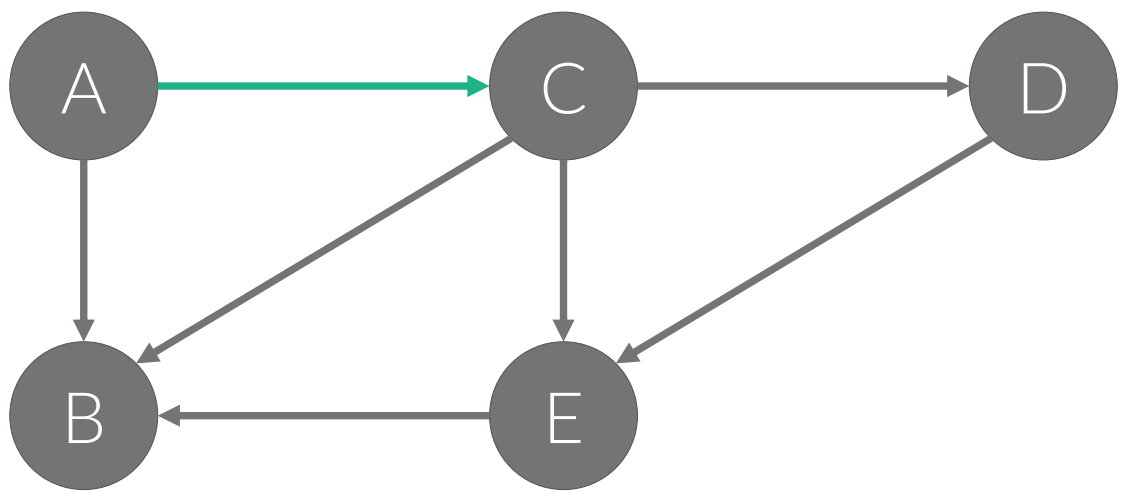
단순 경로와 단순 사이클(SimplePathandSimpleCycle)
• 경로/사이클에서 같은 정점을 두 번 이상 방문하지 않는 경로/사이클
• 특별한 말이 없으면, 일반적으로 사용하는 경로와 사이클은
단순 경로/사이클을 말한다.
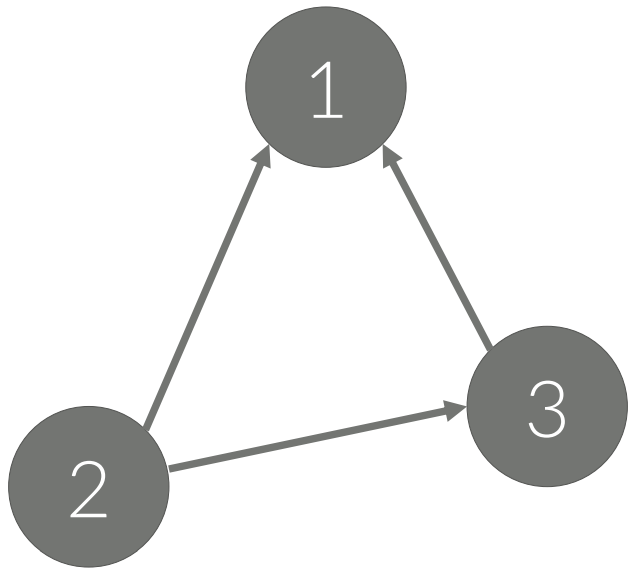
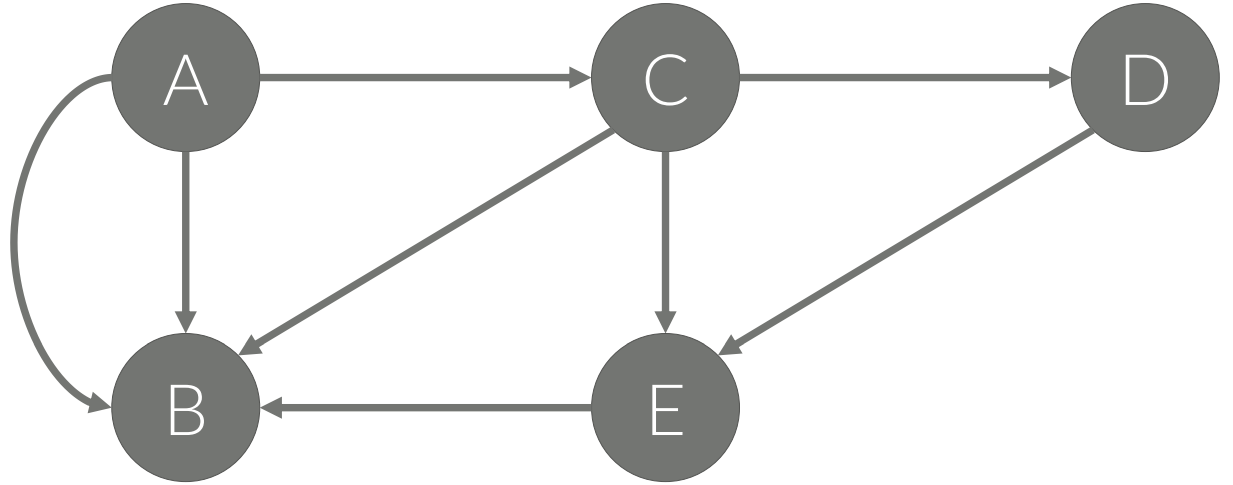
방향 있는 그래프(Directed Graph)
• A → C 와 같이 간선에 방향이 있다.
• A → C는 있지만, C → A는 없다.
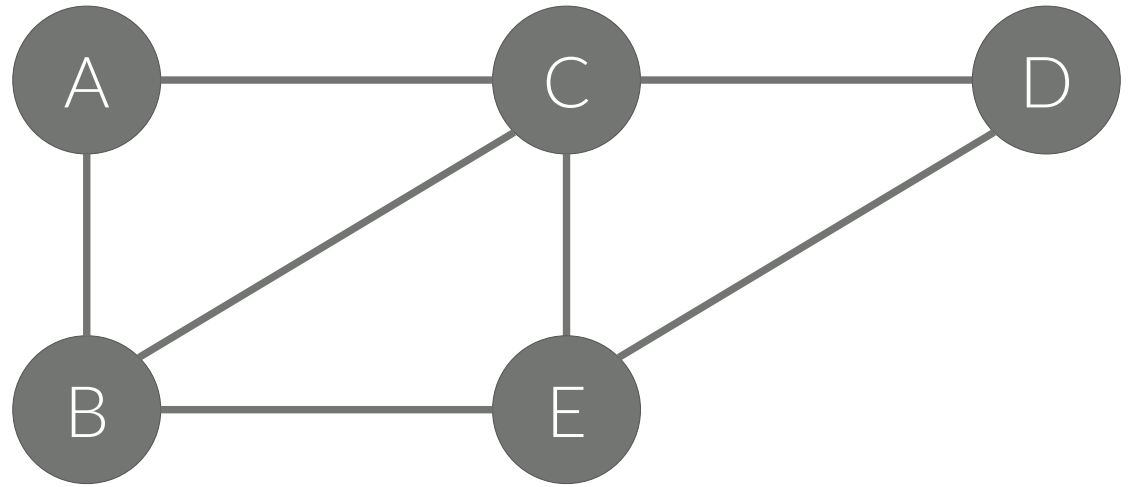
방향 없는 그래프(Undirected Graph)
• A ‒ C 와 같이 간선에 방향이 없다.
• A ‒ C는 A → C와 C → A를 나타낸다.
• 양방향 그래프 (Bidirection Graph) 라고도 한다.
간선 여러개(Multiple Edge)
• 두 정점 사이에 간선이 여러 개일 수도 있다.
• 아래 그림의 A-B는 연결하는 간선이 2개이다.
• 두 간선은 서로 다른 간선이다.
루프(Loop)
• 간선의 양 끝 점이 같은 경우가 있다.
• A → A

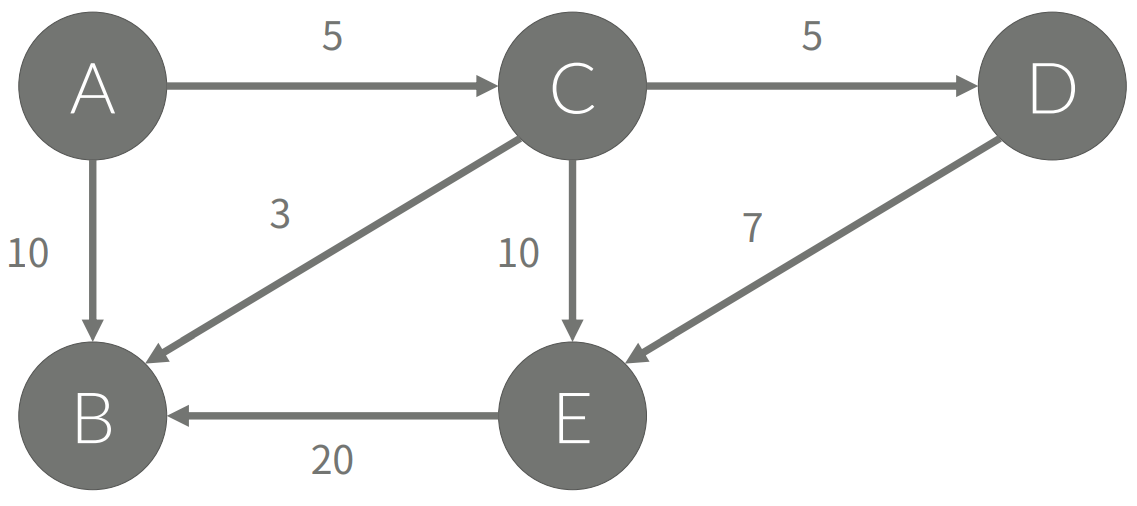
가중치(Weight)
• 간선에 가중치가 있는 경우
• A에서 B로 이동하는 거리, 이동하는데 필요한 시간, 이동하는데 필요한 비용 등등등…
• 가중치가 없는 경우에는 가중치가 1이라고 생각하면 된다.
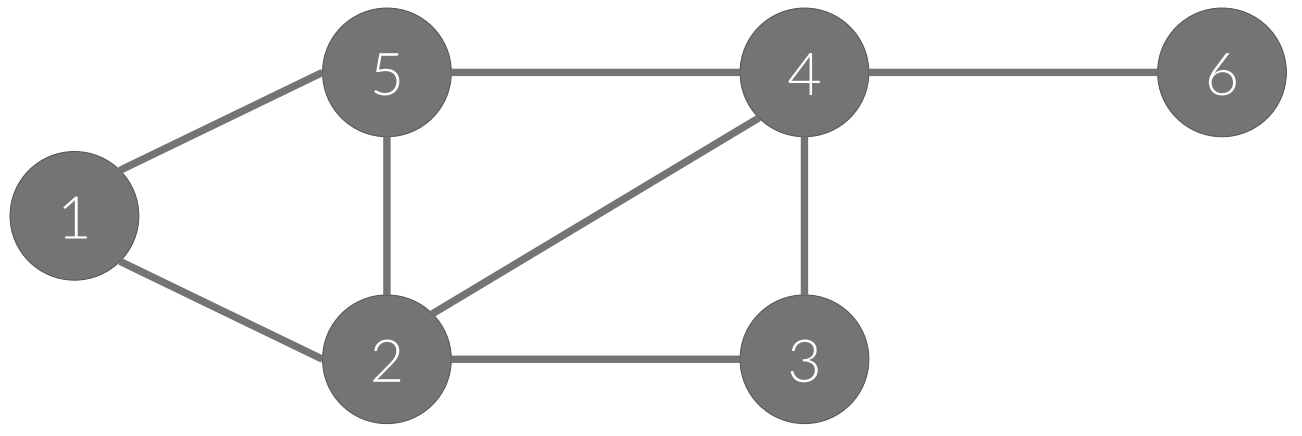
차수(Degree)
• 정점과 연결되어 있는 간선의 개수
• 5의 차수: 3
• 4의 차수: 4
• 방향 그래프의 경우에는 In-degree, Out-degree로 나누어서 차수를 계산한다.
• 4의 In-degree: 3
• 4의 Out-degree: 1

그래프의 표현(Representation of Graph)
• 아래와 같은 그래프는 정점이 6개, 간선이 8개 있다.
• 간선에 방향이 없기 때문에, 방향이 없는 그래프이다.
• 정점: {1, 2, 3, 4, 5, 6}
• 간선: {(1, 2), (1, 5), (2, 5), (2, 3), (3, 4), (2, 4), (4, 5), (4, 6)}

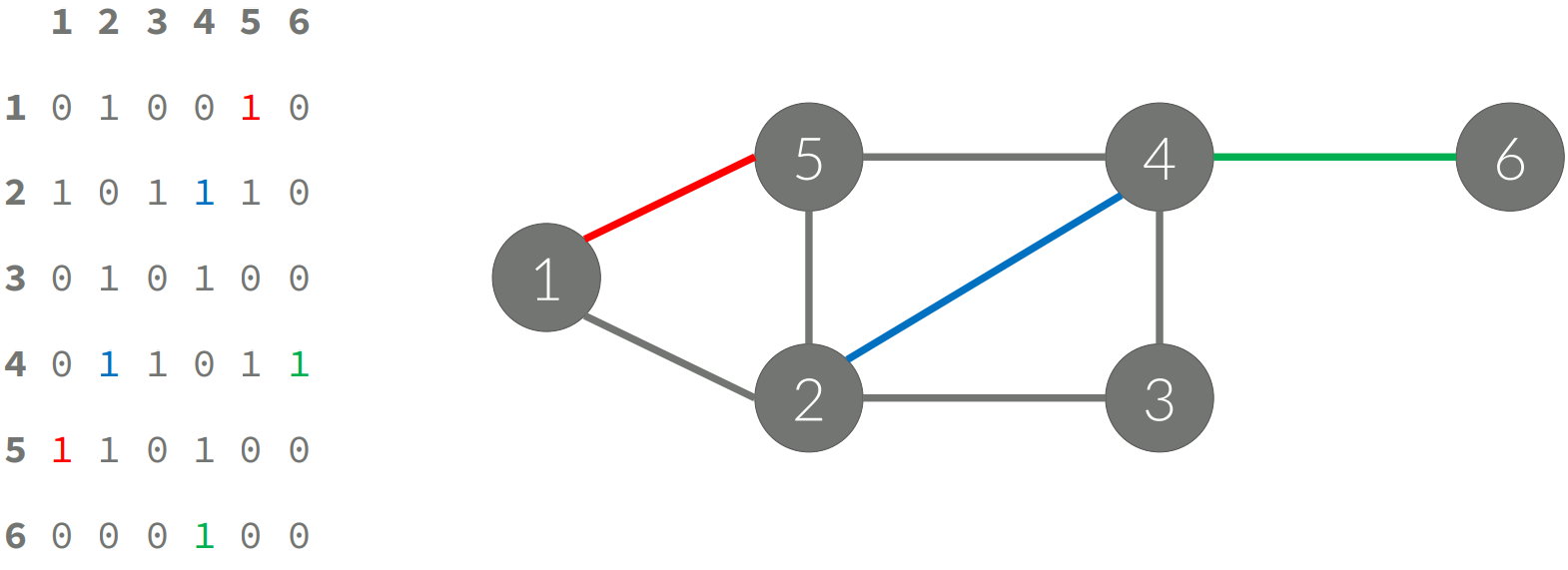
인접 행렬(Adjacency-matrix)
• 가중치가 없는 경우
• 정점의 개수를 V라고 했을 때, V×V 크기의 이차원 배열을 이용한다
• A[i][j] = 1 (i -> j 간선이 있을 때)
• A[i][j] = 0 (i -> j 간선이 없을 때)
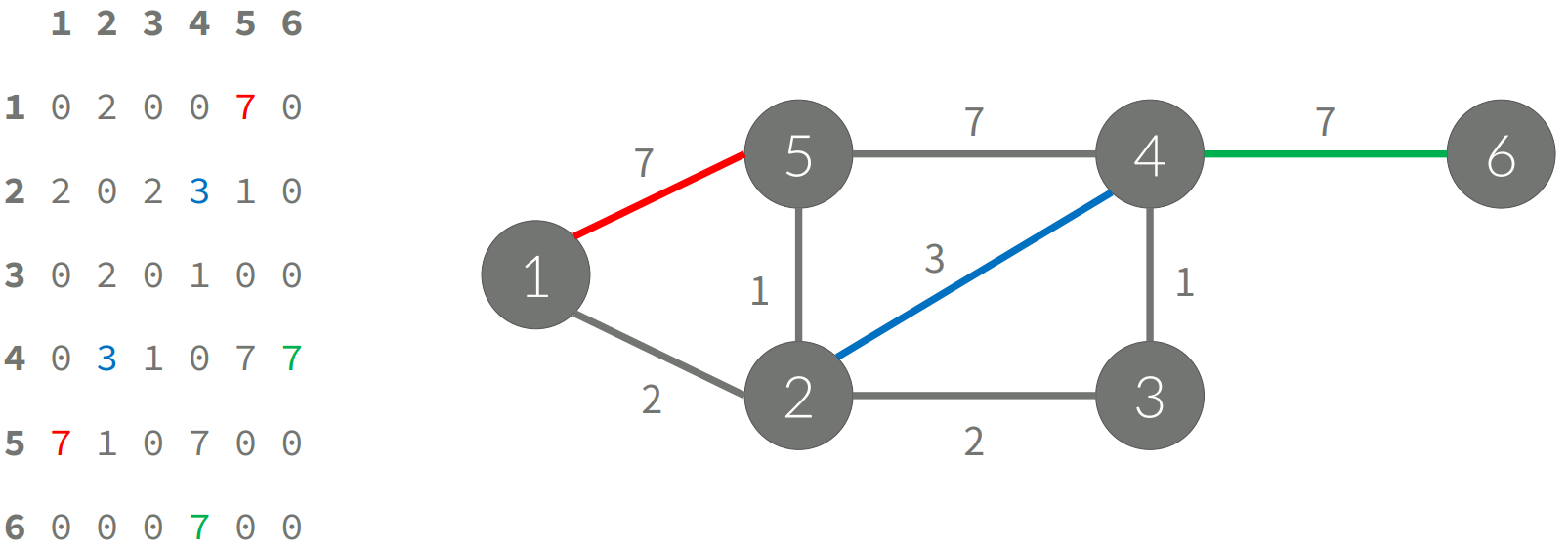
• 가중치가 있는 경우
• A[i][j] = w (i -> j 간선이 있을 때, 그 가중치)
• A[i][j] = 0 (i -> j 간선이 없을 때)
인접 리스트(Adjacency-list)
• 리스트를 이용해서 구현한다.
• A[i] = i와 연결된 정점을 리스트로 포함하고 있음
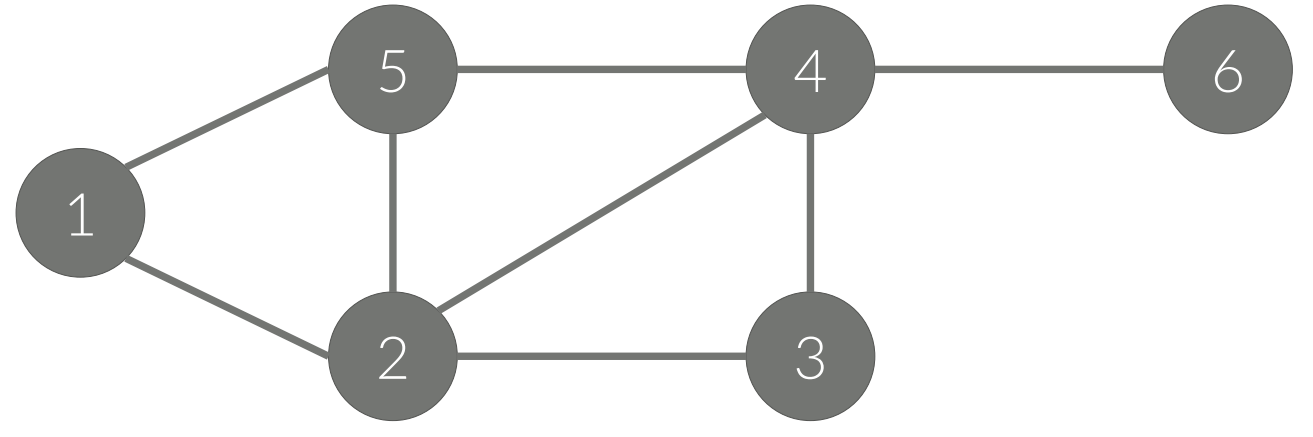
A[1] = 2, 5
A[2] = 1, 3, 4, 5
A[3] = 2, 4
A[4] = 2, 3, 5, 6
A[5] = 1, 2, 4
A[6] = 4
• 리스트는 크기를 동적으로 변경할 수 있어야 한다.
• 링크드 리스트나 길이를 동적으로 변경할 수 있는 배열을 사용한다.
• 가중치가 있는 인접 리스트의 경우
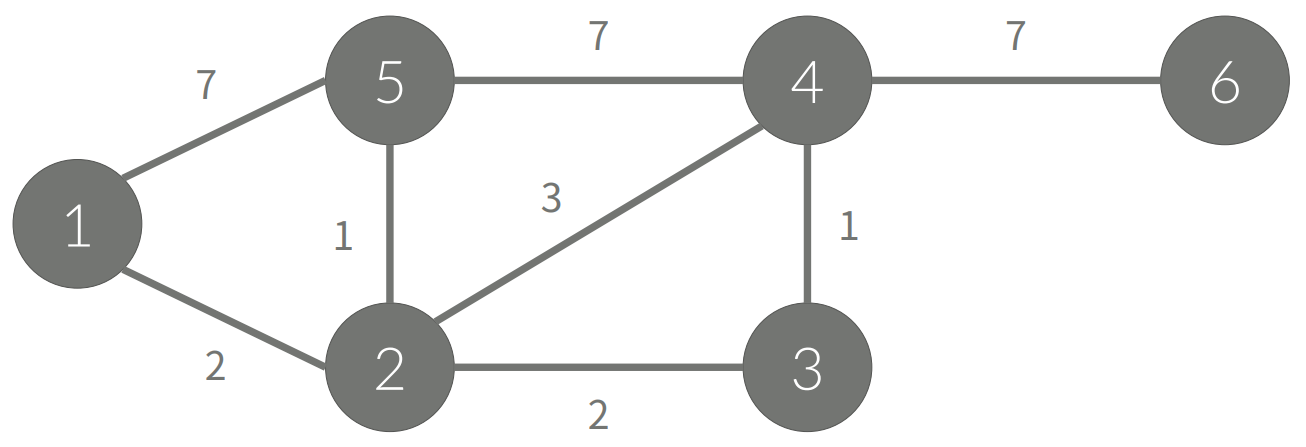
A[1] = (2,2), (5,7)
A[2] = (1,2), (3,2), (4,3), (5,1)
A[3] = (2,2), (4,1)
A[4] = (2,3), (3,1), (5,7), (6,7)
A[5] = (1,7), (2,1), (4,7)
A[6] = (4,7)
간선 리스트(Edge-List)
• 배열을 이용해서 구현한다.
• 간선을 모두 저장하고 있다.
• E라는 배열에 간선을 모두 저장한다.

E[0] = 1 2 E[8] = 4 2
E[1] = 1 5 E[9] = 4 3
E[2] = 2 1 E[10] = 4 5
E[3] = 2 3 E[11] = 4 6
E[4] = 2 4 E[12] = 5 1
E[5] = 2 5 E[13] = 5 2
E[6] = 3 2 E[14] = 5 4
E[7] = 3 4 E[15] = 6 4
• 각 각선의 앞 정점을 기준으로 개수를 센다.

• 누적으로 합하여 개수를 다시 센다.

• i번 정점과 연결된 간선은 E배열에서 cnt[i-1]부터 cnt[i]-1 까지이다
• 1번 정점과 연결된 간선은 0부터 1까지다. E[0]~E[1]
• 4번 정점과 연결된 간선은 8부터 11까지다. E[8]~E[11]
연결 요쇼(Connected Component)
• 그래프가 아래 그림과 같이 나누어져 있지 않은 경우가 있을 수도 있다.
• 이렇게 나누어진 각각의 그래프를 연결 요소라고 한다.
• 연결 요소에 속한 모든 정점을 연결하는 경로가 있어야 한다
• 다른 연결 요소에 속한 정점과 연결하는 경로가 있으면 안된다
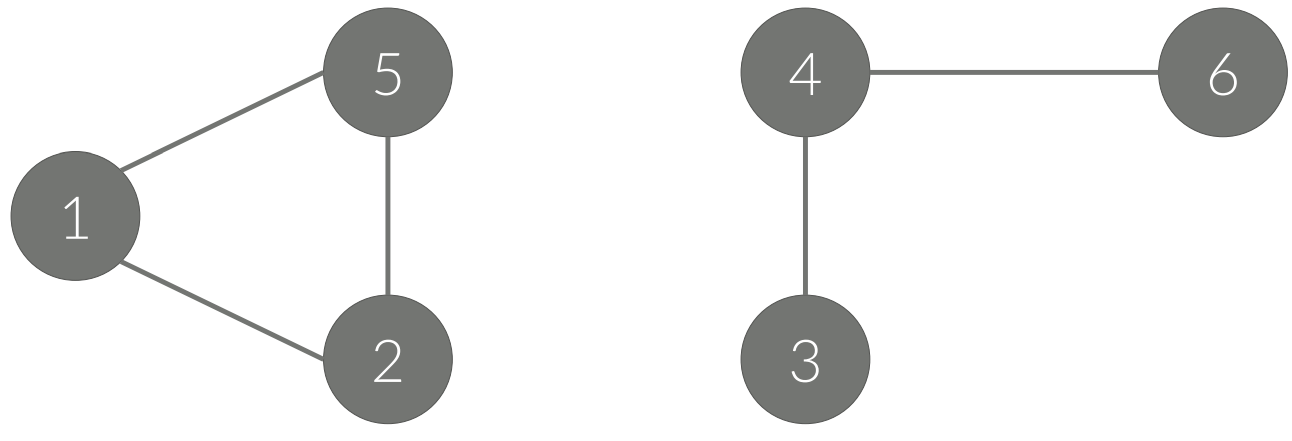
• 아래 그래프는 총 2개의 연결 요소로 이루어져 있다.
• 연결 요소를 구하는 것은 DFS나 BFS 탐색을 이용해서 구할 수 있다.
이분 그래프(Bipartite Graph)
• 그래프를 다음과 같이 A와 B로 나눌 수 있으면 이분 그래프라고 한다.
• A에 포함되어 있는 정점끼리 연결된 간선이 없음
• B에 포함되어 있는 정점끼리 연결된 간선이 없음
• 모든 간선의 한 끝 점은 A, 다른 끝 점은 B로 향함
• 그래프를 DFS또는 BFS 탐색으로 이분 그래프인지 아닌지 알아낼 수 있다.

