이 게시물은 장형기 님의 SLAM 기술 면접 질문 100선에 대한 제 나름대로의 답을 정리한 것입니다.
기본 개념: Epipolar Geometry
Epipolar Geometry란?
서로 다른 시점(View)에서 동일한 3D 점을 관찰할 때,
이 점들이 각 이미지에 투영된 좌표들 사이의 기하학적 제약 조건을 설명하는 이론입니다.
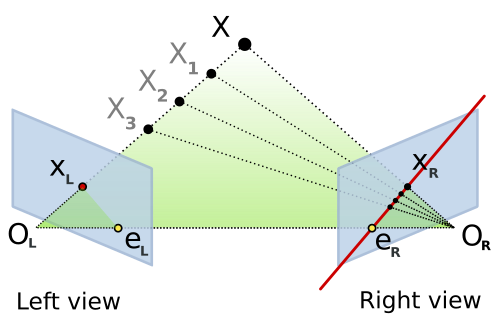
구성요소 요약
- Epipole: 한 카메라의 중심이 다른 카메라 이미지 평면 위에 투영된 점
- Epipolar Line: 한 이미지의 점이, 다른 이미지 상에서 가질 수 있는 가능한 위치가 제한된 직선
- Epipolar Plane: 두 카메라 중심과 하나의 3D 점이 이루는 평면
- Epipolar Constraint: 두 점의 대응 관계는 아래 수식과 같은 기하학적 조건을 만족해야 함
이 식은 다음을 의미합니다:
x'은 x로부터 계산된 epipolar line 위에 있어야 한다.
epipolar line은 ( Fx )로 계산되며, 이때 사용되는 F matrix를
Fundamental matrix 또는 Essential matrix라고 합니다.
Fundamental Matrix와 Essential Matrix
Fundamental Matrix
Fundamental matrix는 두 카메라의 내부 파라미터 없이
두 영상에서의 대응점 간 기하학적 제약(F Epipolar Constraint)을 표현하는 3X3 행렬입니다.
❓ 3×3 행렬이면 회전 행렬인가요?
저도 처음엔 그렇게 생각했지만, Fundamental matrix는 회전과는 무관하며
epipolar line을 정의하는 제약 조건을 만족시키기 위한 행렬입니다.
8-point 알고리즘
우리는 8개의 대응점만으로 Fundamental matrix를 계산할 수 있습니다.
이때는 내부 파라미터 없이 계산됩니다.
❓ 왜 3×3 행렬(총 9개 원소)을 8개 점으로 계산할 수 있나요?
Fundamental matrix는 scale에 대해 동차적(homogeneous)이기 때문에
다음과 같은 관계가 성립합니다:
즉, 임의의 상수배를 곱해도 의미는 동일하므로,
실제로는 자유도가 8개뿐이고, 8개의 점만으로도 계산할 수 있는 것입니다.
7-point 알고리즘
Fundamental matrix는 기하학적 특성상 항상 rank 2여야 합니다.
이는 epipolar line이 반드시 존재해야 한다는 의미이고,
다음과 같은 수학적 제약식으로 표현됩니다:
이 비선형 제약 조건을 추가하면, 필요한 대응점 수가 7개로 줄어듭니다.
즉, 7개의 점만으로도 ( F )를 구할 수 있는 방법이 바로 7-point 알고리즘입니다.
📌 단, 이 방법은 비선형 방정식을 풀어야 하므로,
경우에 따라 1개 또는 최대 3개의 해(F)가 나올 수 있습니다.
요약표
| 알고리즘 | 제약 조건 | 필요 대응점 수 | 계산 방식 |
|---|---|---|---|
| 8-point | 없음 (선형식) | 8쌍 | 선형 해법 (Ax = 0) |
| 7-point | (\det(F)=0) (비선형) | 7쌍 | 비선형 방정식 풀기 |
Essential Matrix
Essential Matrix E는 두 대의 내부 파라미터(K)로 보정된
카메라 간의 기하학적 관계를 나타내는 3X3 행렬입니다.
여기서 x,x'는 정규화된 카메라 좌표계에서의 점입니다.
5-point 알고리즘
보정된 좌표계에서 5개 이상의 대응점 쌍이 주어지면
5-point 알고리즘을 사용하여 Essential Matrix를 계산할 수 있습니다.
계산 순서
- 내부 파라미터 행렬 K로 점을 정규화
-
Epipolar constraint 을 만족하는 E 계산
-
E -> 자세(R,t) 추정
2번 과정에서 우리는 5개의 점을 쓰는데
7-point 알고리즘까지 자유도를 낮추는 방식은 같지만
5-point에서는 특수한 Singular value 구조를 갖는 것을 활용합니다.
constraint: Essential Matrix의 singular value는
이것까지 활용하면 자유도 2가 더 줄어들어 5쌍의 대응점만 가지고도 Matrix를 계산할 수 있습니다.
❓ 그럼 Fundamental Matrix도 5-point 알고리즘으로 구할 수 있나요?
5-point 알고리즘은 Essential Matrix에만 사용가능합니다.
Fundamental matrix에는 내부 파라미터 정보가 없기 때문에 5개의 대응점으로 불충분합니다.
내부 파라미터가 있을 경우
-
픽셀 좌표를 정규화된 좌표로 변환
-
렌즈 왜곡, 초점 거리, 주점 정보 등으로 인해 생기는 비선형성을 제거
-
좌표계를 내부 좌표계로 통일
이러한 점을 이용하여 Essential Matrix에서는 더 적은 대응점으로 계산을 할 수 있는 것입니다.
3줄 요약
-
두 시점으로 본 3d point를 epipolar geometry로 표현
-
카메라 내부 파라미터 안쓰면 Fundamental Matrix
-
카메라 내부 파라미터 쓰면 Essential Matrix
