Homography matrix가 무엇인가요?

이 게시글은 장형기님의 SLAM 기술면접 질문 100선에 대한 제 나름의 답을 정리한 것입니다.

---

정의

Homography는 두 평면 사이의 Projection 변환 관계를 나타내는 용어입니다.
다시 말해, 한 평면을 다른 평면에 projection했을 때, 두 평면 상의 대응점들 사이에 성립하는 변환 관계를 의미합니다.

이렇게 두 사진 Projection 된 좌표 값 사이의 변환관계를 나타낼 수 있는 matrix H를 homography matrix라고 합니다.

---

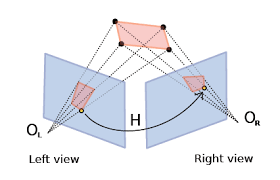
❓ 그럼 어디에 쓰나요?

Homography matrix의 장점은 특정 조건에서 변환 관계를 3D에서 찾을 필요가 없다는 점입니다.

일반적으로 두 이미지의 대응 관계를 구하려면 Epipolar geometry를 사용합니다.
Epipolar geometry는 3D를 활용하는 것이기 때문에 계산 과정이 길고 복잡합니다.

하지만, 장면이 하나의 평면이거나 순수 회전이라면 이 3D 복원 과정을 거칠 필요 없이 바로 2D $\rightarrow$ 2D 매핑이 가능합니다.
즉, 대응점 몇 개만으로 두 이미지의 변환 행렬 $H$를 추정하고, 이를 사용해 전체 점 변환이 가능합니다.

---

❓ 왜 가능한가요?

Homography matrix는 강력한 Constraint를 통해서 계산하게 됩니다.

1. 하나의 3D 평면을 보는경우

   • 물체가 하나의 평면 위에 있다고 가정하면, 각 점의 깊이 정보를 몰라도 평면 방정식으로 대체할 수 있습니다.

2. translation없이 순수 회전을 한다

   • translation이 없으면 Projection 식에서 깊이 Z가 사라져, 장면 전체의 모든 점이 깊이에 관계없이 동일한 2D 변환을 갖게 됩니다.

둘 중의 한 constraint는 만족해야 사용할 수 있습니다.

한 벽면을 보고 있으면 우리가 보는 물체가 하나의 평면 위에 붙어 있다는 것을 알기 때문에 우리가 움직이더라도 저 물체 point 사이의 관계를 알고 있어서 계산하기가 편해집니다.

같은 이유로 내가 순수하게 회전만 한다면 모든 점들이 동일한 projection 변환을 가지기 때문에 우리는 이 constraint를 활용하여 homography matrix를 만들 수 있습니다.

---

❓ 어떻게 하나요?

1. 일반적인 카메라 투영식

   카메라는 3D점 (X,Y,Z)를 내부 파라미터 K와 외부 파라미터 $[R|T]$를 이용해 2D 이미지 좌표 $(u,v)$로 변환합니다.
   (s는 스케일 인자입니다.)

2. 두 시점의 카메라 포즈

   같은 3D 점을 두 카메라가 본다면 이렇게 나타낼 수 있습니다.

   첫 번째 카메라:

   $s_1 \mathbf{x}_1 = K_1 [I \;|\; 0] \mathbf{X}_\text{world}$

   두 번째 카메라:

   $s_2 \mathbf{x}_2 = K_2 [R \;|\; T] \mathbf{X}_\text{world}$

3. 첫번째 카메라에서의 3D 점 표현

   첫번째 카메라의 이미지 좌표 $x_1$을 reprojection하여 3D 점을 만들면 이렇게 됩니다.

4. 두번째 카메라 투영식에 대입

   이렇게 구한 3D 점을 두번째 카메라에 투영하면 아래 식처럼 나옵니다.

   $s_2 \mathbf{x}_2 = K_2 \left( R \cdot (Z \cdot K_1^{-1} \mathbf{x}_1) + T \right)$

   이렇게 구한 식에는 Z값이 들어있기 때문에 각기 다른 Z값을 가지고 있다면 다른 변환 관계를 갖게 됩니다.

5. 평면 제약 적용
   만약 모든 점이 하나의 평면 위에 있다면, 깊이 $Z$를 평면 방정식으로 표현할 수 있습니다.

   평면 방정식:

   $n^\top X_c = d$

   대입 후:

   $Z = \frac{d}{n^\top K_1^{-1} \mathbf{x}_1}$

6. Homgraphy 유도
   Z를 두번째 카메라 좌표 투영식에 대입을 한 후 분자만 정리하게 되면 (어차피 분모는 scale factor로 처리)
   이런 식이 나오게 됩니다. 그러면 $x_1$에 어떤 행렬을 곱하여 $x_2$를 구하게 되고 이것을 Homography matrix라고 합니다.

   $\mathbf{x}_2 \sim K_2 \left( R - \frac{T n^\top}{d} \right) K_1^{-1} \mathbf{x}_1$

7. 최종 형태

❓ 순수 회전은요??

순수 회전은 이제 4번 식의 T가 사라집니다.
그렇다면 Z는 그냥 scale factor처럼 사용되게 되어 무시하고 계산하면 됩니다!

이러한 형태로 나오게 됩니다.