이 논문은 2022년에 CVPR에 나온 논문입니다.
UC 버클리에서 썼네요.
Introduction
이 연구의 시작은 NeRF가 너무 느리다는 것에 있습니다.
너무 느리기 때문에 사용할 수가 없어 이것을 빠르게 하기 위해 Plenoxel을 제안합니다.
이 논문은 학습을 할 때 신경망 없이 시점에 따라 달라지는 sparse voxel grid를 기반으로 하여 explicit한 표현을 합니다. 이를 통해 3D 볼륨 재구성의 최적화 시간은 크게 단축하면서 사실적인 랜더링 품질을 유지하는 효율적인 방법을 제시합니다. 결국 빠르게 하려고 제안한 것입니다. 이 논문은 제가 이전에 review했던 MERF의 전 논문으로 MERF가 이 논문과 비슷한 점이 많아 읽게 되었습니다. SNeRG도 읽어야하는데 읽을게 많네요.
Method
이 model은 sparse voxel grid에 scalar opicity와 spherical harmonic coefficients의 vector를 저장합니다.
이 저장된 값들을 이용하여 임의의 position을 interpolation을 통해 표현하게 됩니다.
rendering loss를 통해 voxel 안의 값들을 학습하게 됩니다.
-
Vloume Rendering
Plenoxel에서도 NeRF와 같은 미분가능한 volume rendering model을 사용합니다.
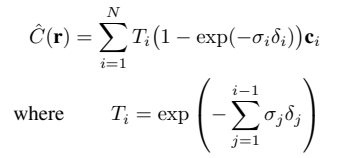
이 식은 완벽하진 않지만 미분이 가능하고 3D model을 업데이트 할 수 있기 때문에 사용한다고 합니다. -
Voxel Grid with Spherical Harmonics
PlenOctree와 비슷하게 sparse voxel grid를 사용합니다. 그러나 trilinear interpolation을 잘 활용하기 위해서 data structure를 octree로 사용하지 않습니다.
대신 3D index array를 pointer와 분리된 data어레이에 저장합니다.
PlenOctree와 마찬가지로 각각의 얻어진 복셀은 opacity와 spherical harmonic coefficient를 저장합니다.
SH는 구 위에서 정의된 함수들의 직교 기저를 만들고 색상의 방향성 변화를 효율적으로 모델링하기 위해 사용됩니다.
2차원의 SH를 사용하고 각 생상 채널에 대해 9개의 계수를 최적화합니다. Voxel에는 27개의 SH 계수가 할당됩니다. 이것을 통해 시점에 따라 색상이 어떻게 변하는지를 표현할 수 있습니다.
PlenOctree는 하나의 Voxel 안에서는 SH와 opacity가 일정하다고 가정하지만
Plenoxel의 경우 voxel안에서도 모서리에 저장된 값을 interpolation하기 때문에 연속적인 색 표현을 합니다. -
Interpolation
가장 가까운 8 voxel에 저장된 harmonic coefficients와 opacity의 interpolation을 통해 sample point의 opacity와 color를 계산합니다. trilinear interpolation이 nearest neighbor interpolation보다 훨씬 더 좋은 성능을 내기 때문에 이 논문에서는 trilinear interpolation을 사용합니다.
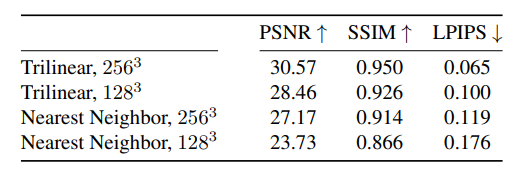
두 interpolation을 비교한 표이고 trilinear interpolation이 더 좋은 성능을 내는 것을 볼 수 있습니다. -
Coarse to Fine
High resolution의 reconstruction을 하기 위해 coarse-to-fine 전략을 사용합니다.
이 전략은 dense grid를 low resolution에서 시작하여 최적화하고 필요없는 voxel을 제거한 후 남은 voxel을 refine하고 계속 최적화하는 것입니다. -
Optimization
이 model은 voxel opacity와 spherical harmonic coefficients를 최적화 합니다.
최적화 할 때 rendering 된 pixel color에 대해 MSE를 사용하고 total variation regularization을 사용합니다. TV regularization은 gradient가 커지는 것도 loss term으로 넣어 gradient를 최소화하는 방향으로 최적화를 하게 하여 noise를 제거해주고 edge를 보존해줍니다.
Voxel coefficient들을 바로 최적화 하는 것은 너무 큰 계산량이 들기 때문에 쉽지 않습니다.
그렇기 때문에 보통은 second order optimization을 사용하지만 고차원 optimization에서는 계산량이 많아 이것도 쉽지 않습니다. 그래서 plenoxel은 RMSProp을 사용하여 이 문제를 해결합니다. 이전 optimization 기울기를 활용하는 딥러닝 기반 최적화 알고리즘인데 진동을 억제하고 안정적인 수렴을 제공하는 것으로 알려져 있습니다.
-
Unbounded Scenes
보통 NeRF는 범위가 고정되어 있는 Scene에서 사용됩니다.
더 넓은 범위에서 사용하기 위해선 unbounded scenes에 대한 Representation도 가능해야합니다.
이를 위해 사용한 model은 Multi sphere image background model입니다.
이 model에서 voxel들이 구형으로 변형되어 인덱싱을 하게 됩니다.
총 64개의 구체를 배치하는데, 이 구체들은 반경의 역수로 선형적으로 배치됩니다.
메모리를 절약하기 위해, 색상에 대해서는 RGB 채널만 저장하고 불투명도 threshold를 사용하여 sparse하게 저장합니다. -
Regularization
TV regularization에 대한 중요성에 대한 그림은 다음과 같습니다.

TV 정규화는 앞에 설명했던 것과 마찬가지로 장면에서 부드러움을 유도하는 역할을 하며, 모든 장면에서 사용됩니다. 이는 모델이 과도하게 변동하지 않도록 하고, 노이즈를 줄이는데 기여합니다.
Cauchy손실 함수는 SNeRG model에서 사용된 sparse constraint를 기반으로 합니다.
이 정규화는 모델의 sparsity를 유지하도록 도와주며, 특히 실제 장면이나 360도 장면에서 사용됩니다. 이는 PlenOctree에서도 사용되었고 메모리 절약 및 업샘플링 시 품질 저하를 줄이는데 도움을 줍니다. 식은 다음과 같습니다.
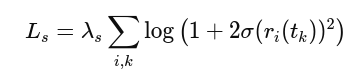
베타 분포 정규화
360도 장면에서는 베타 분포를 기반으로 한 정규화가 추가적으로 사용됩니다.
이 정규화는 전경과 배경을 명확하게 구분하는데 도움을 주며, Neural Volumes에서 사용된 방식과 유사합니다. 이를 통해 전경은 완전히 불투명하거나 완전히 비어 있도록 유도됩니다.
식은 다음과 같습니다.

- Implementation
sparse voxel volume rendering이 autodiff 라이브러리에서 잘 지원되지 않기 때문에 이를 해결하기 위해 PyTorch CUDA 확장 라이브러리를 개발했습니다.
Plenoxel 모델의 기울기가 매우 빨리 희소해지기 떄문에 1~2분 내에 최적화가 진행되면, 10% 미만의 Voxel만이 nonzero기울기를 갖게 됩니다. 즉, 초기 최적화 단계에서만 대부분의 Voxel이 영향을 받고 이후에는 매우 적은 수의 Voxel만이 학습에 영향을 끼칩니다.
