MERF: Memory-Efficient Radiance Fields for Real-time View Synthesis in Unbounded Scenes
Paper
Introduction
Implicit Neural representation인 NeRF의 단점을 고친 논문입니다.
NeRF의 경우 시간이 너무 오래 걸리고 large Scene을 나타낼 수 없다는 단점이 있습니다.
이것을 해결하기 위해 MERF 논문은 baking 방법과 이 과정에서 생기는 메모리 문제를 해결하는 방식을 제안하여
효율적이고 빠른 representation을 해냈습니다.
Preliminaries
NeRF 식을 간단히 살펴보자면
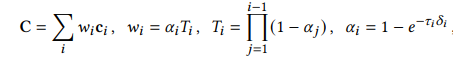
ray위의 color와 투명도 T를 통해 자세한 표면 표현이 가능해지는 representation임을 알 수 있습니다.
하지만 이것은 모든 ray에 대해 일일이 계산을 해줘야 하기 때문에 오래 걸린다는 단점이 있습니다.
이것을 해결하기 위해 나온 것이 SNeRG라는 논문인데 이것은 3d field의 density와 color, feature를 학습합니다. 이것을 그냥 학습만 하는 것이 아니라 학습한 결과물들을 grid의 저장을 하고 그 저장된 값을 불러와 rendering을 합니다. rendering을 할 때마다 계산을 하는 것이 아니라 저장된 값을 불러오기 때문에 훨씬 시간이 빨라지지만 메모리를 많이 잡아먹는다는 단점이 있습니다. SNeRG는 unbounded된 공간을 표현하기 위해 contraction function을 사용하는데 그것은 다음과 같은 식입니다.
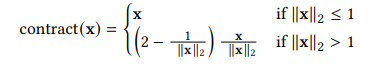
이를 통해 무한대의 공간을 수렴할 수 있도록 하는 것입니다.
Scene Representation
MERF는 unbounded scene에 대한 실시간 rendering을 가능하게 한 논문입니다.
- Volume Parameterization
MERF는 장면을 volume density로 표현하게 됩니다. 이렇게 되면 자세한 표현이 가능하겠지만 계산량이 많아진다는 단점이 있습니다. 이를 해결하기 위해 MERF는 volume은 parameterization을 하게 됩니다.
이것은 3d 공간은 저해상도의 3d voxel grid와 3개의 고해상도 2d grid로 구성하는 것을 말합니다.
각 그리드의 component는 c개의 채널을 저장하는 벡터로 이루어져 있습니다.
3d 공간 각 지점에서 c-vector는 3d voxel grid와 고해상도 2d grid의 합으로 표현됩니다.
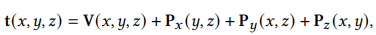
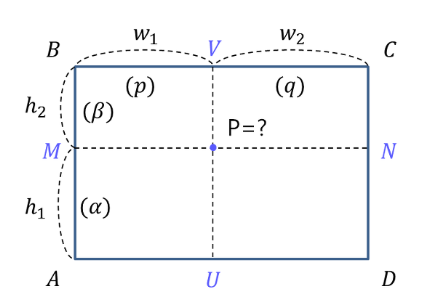
3d grid는 trilinear interpolation을 통해 값을 얻고
2d grid는 bilinear interpolation을 통해 값을 계산합니다.
이렇게 계산된 값들이 grid에 들어가고 그것을 통해 3차원 공간을 표현을 하게 됩니다.
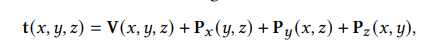
interpolation을 통해 grid에 저장된 값들을 모두 더해 그 좌표에 해당되는 정보를 만들게 됩니다.
얘를 들어 (1,1,1)의 정보를 담고 싶으면 low resolution V(1,1,1)의 정보와 xPlane(1,1), yPlane(1,1),zPlane(1,1)의 정보를 합쳐서 고해상도의 정보를 효율적으로 계산할 수 있다는 것입니다.
- Piecewise-projective Contraction
Mip-NeRF도 unbounded Scene을 표현하려고 했는데 contraction function을 활용하였습니다.
하지만 여기서 사용한 contraction function은 공간을 radius-2 ball에 정의합니다.
이렇기 때문에 공간이 discrete한 voxel로 정의가 되지 않습니다.
이렇게 되면 공간에 빈공간이 생길 경우 volume rendering에 문제가 생긴다고 합니다.
그리고 intersection을 효율적으로 계산하기 위한 다른 기법을 사용하게 됩니다.
이를 방지하기 위해 이 논문에서는 공간을 새롭게 정의합니다.
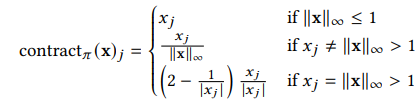
이렇게 정의하면 수축된 공간에서도 광선이 직선처럼 움직여서 ray-AABB 교차 테스트를 그대로 사용할 수 있다고 합니다.
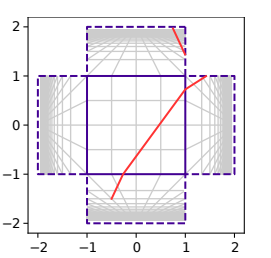
보시듯이 구가 아니라 상자 모양으로 정의 되기 때문에 직선성이 보존 되는 것을 볼 수 있습니다.
이렇기 때문에 직선성을 유지한 상태로 unbounded scene을 표현할 수 있습니다.
Training and Baking
- Efficient Training
high resolution의 large-scale scene을 rendering하려면 memory가 굉장히 많이 쓰일 것입니다.
학습동안에는 backpropagation 값 저장하고 한다고 훨씬 더 많은 memory를 사용합니다.
이를 위해 효율적인 training 방법이 꼭 필요합니다.
계층적 샘플링 방식을 사용하여 ray sampling을 효율적으로 진행하였고
랜더링 시 빈공간이 있는 경우 그 부분을 skip하여 학습의 효율을 높였습니다.
hash encoding을 통해 input값을 처리하면서 더 효율적인 학습을 진행하였습니다.
- Quantization
grid의 값들을 그냥 저장하게 되면 memory를 되게 많이 차지하게 됩니다.
양자화를 통해 값들을 변환 시켜 저장하면 memory 효율성을 높일 수 있습니다.
각 grid에 저장된 값들을 sigmoid에 통과 시켜 [0,1] 범위로 변환하고 양자화를 적용시켜
1바이트 값으로 변환합니다. 양자화된 값을 다시 원하는 범위로 맵핑하기 위해 Affine 변환을 적용하여 최종적으로 원하는 범위에 맞춥니다.
그냥 값을 양자화하여 저장한다고 생각하시면 됩니다. 뭐 양자화 식에 대해선 잘 몰라도 될 것 같습니다.
memory효율은 높였지만 미세한 값을 표현하지 못한다는 점은 단점입니다.(실시간성을 위해 이 정도는 포기해도 될 것 같다고 생각하였습니다.)
- Baking
저장을 미리 하는데 이렇게 되면 rendering 속도는 빨라지지만 memory를 많이 쓰게 됩니다.
이 단점을 없애기 위해 여러 방법을 사용합니다.
occluded voxel이나 훈련 중에 샘플링되지 않은 영역은 저장하지 않도록 하여 memory 효율을 높입니다.
점을 기준으로 볼륨 랜더링을 할때 weight와 불투명도를 가지게 되는데 이 값들을 보고 너무 투명하거나 밀도가 적은 포인트는 날리면서 빈공간을 계산하지 않게 해줍니다. 이렇게 되면 memory의 효율성을 크게 높일 수 있습니다.
Realtime Rendering
실시간 rendering을 위한 ray marching 기법을 설명하고 있습니다.
여기서는 다중 해상도 점유 그리드를 사용하여 효과적인 공간 skip을 한다고 합니다.
그 과정을 살펴보겠습니다.
먼저 baking 과정에서 우리는 기본 해상도에 미리 계산된 값들을 저장해놨습니다.
그 grid에 max pooling을 사용하여 다양한 크기의 점유 그리드를 생성합니다.
이렇게 다양한 크기의 grid를 통해 효율적으로 공간을 나타낼 수 있다고 합니다.
먼저, 낮은 해상도의 grid를 살펴보며 빈공간을 살펴봅니다. 그렇게 되면 큰 빈공간들을 금방금방 날리게 되고 이제 차지된 공간이라고 확정이 되면 그 부분에 대한 고해상도를 차근차근 살피면서 연산량을 줄이면서도 정확한 결과를 얻을 수 있습니다.
사실 이 논문은 계속 빈공간만 날리는데 집중을 하는 것 같습니다.
추가적으로 사용하는 기법에 loop unrolling, memory layout최적화, 빠른 행렬 곱셈 등이 있는데 그냥 알아만 두면 될 것 같습니다.
