[코테]22-그래프의 표현

Hyewon·2021년 4월 5일

codingtest

목록 보기

23/25

그래프의 표현

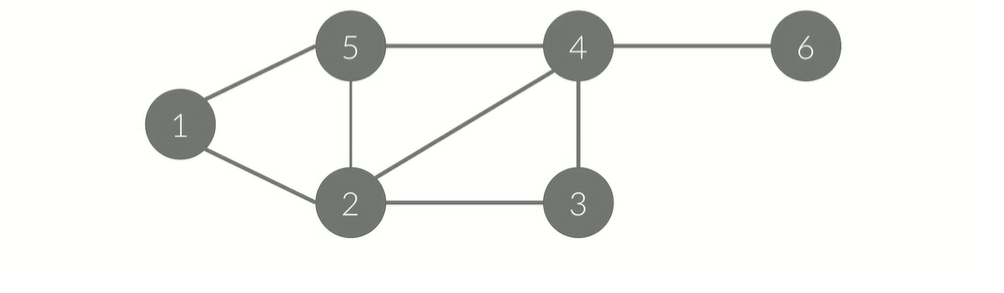
그래프 : 정점 / 간선을 저장.

정점이 6개, 간선이 8개 있다.

간선에 방향이 없기 때문에, 방향이 없는 그래프.

정점의 저장 : 개수 V ( 1-V or 0-(V-1) )

간선의 저장 : 개수 E

간선의 저장 -> 효율 : 한 정점 V와 연결된 모든 정점을 구하는 시간

간선의 방향 -> 방향 그래프 / 양방향 그래프.
-> 방향이 없는 그래프여도 전부 방향 그래프로 표현함.

* 그래프 효율적으로 저장

1) 인접 행렬

2차원 행렬을 이용해서 구현.
A[i][j]=1 : 연결되어 있으면 1 , 아니면 0
가중치가 없으니까 1 or 0으로 넣으면 됨.
가중치가 있는 경우에는 A[i][j] > 0 이라면 연결됨. 그리고 그 값은 가중치.
방향이 없는 그래프는 A[i][j] == A[j][i] 해주어야 함! (왜냐면 양방향이기 때문)

장점 : 임의의 두 정점 사이에 간선이 있는지 없는지 쉽게 판단 가능.
=> 시간복잡도 O(1)

2) 인접 리스트

리스트를 이용해서 구현.
A[i] = i와 연결된 정점을 리스트로 포함하고 있음.
공간 : E
효율성 : O(V의 차수)

시간복잡도 : O(차수)
=> 인접리스트로 구현하는 것이 훨씬 더 빠름.

각각 연결된 간선이 다르기 때문에 크기가 다름 즉, 동적으로 변경가능해야함.
배열 크기가 다르기 때문에 ArrayList 사용.

간선리스트
ArrayList를 사용할 수 없어서 Linked List 구현해야하는데 자신이 없을 때 사용함.
배열을 이용해서 구현.
간선을 모두 저장하고 있음.
E라는 배열에 간선을 모두 저장.
각 간선의 앞 정점을 기준으로 개수를 센다.
한 정점과 연결된 모든 정점을 효율적으로 찾는 것.

ABCDE (13023)

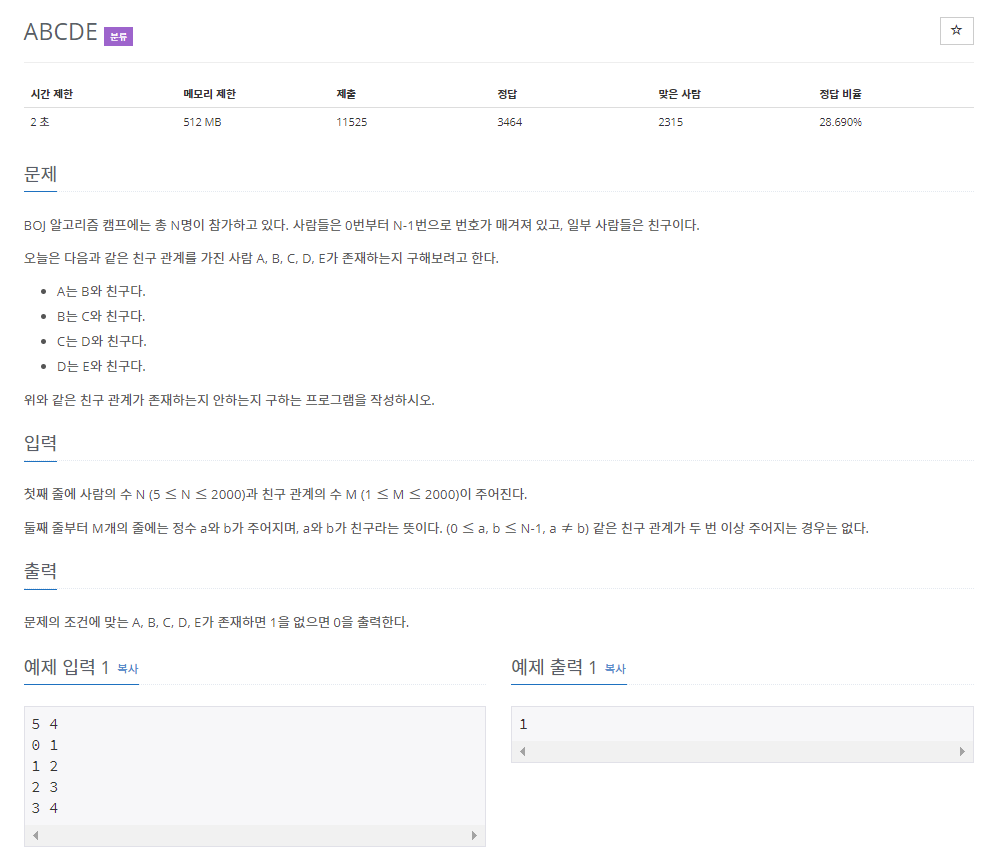
총 N명의 친구 관계가 주어졌을 때 다음과 같은 친구 관계가 존재하는지 구하는 문제.
A는 B와 친구다.
B는 C와 친구다.
C는 D와 친구다.
D는 E와 친구다.

인접 행렬 : 임의의 두 정점 사이의 간선이 있는지 확인 O(1)
인접 리스트 : 한 정점과 연결된 모든 간선 O(차수)
간선 리스트
A->B->C->D->E
A->B (간선리스트)
C->D (간선리스트)
D->E를 찾는다. (인접리스트)

왜 이렇게 푸는지 이해가 안가서 좀 찾아봤더니 DFS를 이용해서 주로 풀더라.. 근데 다음 강의에서 DFS를 사용하니까 여기서는 간선리스트 + 인접리스트를 이용해서 푸는 방법을 알려준 것 같았다...

import java.util.*;

class Edge{
	int from, to;
	Edge(int from, int to){
		this.from = from;
		this.to=to;
	}
}
public class Main {
	public static void main(String[] args) {
		Scanner sc= new Scanner(System.in);
		int n= sc.nextInt();
		int m= sc.nextInt();
		boolean a[][]=new boolean[n][n]; //인접행렬
		ArrayList<Integer> g[] = new ArrayList[n];
		ArrayList<Edge> edges = new ArrayList<Edge>();
		for(int i=0;i<n;i++) {
			g[i] = new ArrayList<Integer>();
		}
		for(int i=0;i<m;i++) {
			int from =sc.nextInt();
			int to = sc.nextInt();
			edges.add(new Edge(from, to));
			edges.add(new Edge(to, from));
			a[from][to] = a[to][from] = true;
			g[from].add(to);
			g[to].add(from);
		}
		m *=2;
		
		for(int i=0;i<m;i++) {
			for(int j=0; j<m; j++) {
				int A= edges.get(i).from;
				int B= edges.get(i).to;
				int C= edges.get(j).from;
				int D= edges.get(j).to;
				if(A==B || A==C || A==D || B==C || B==D || C==D) {
					continue;
				}
				if(!a[B][C])	continue;
				for(int E : g[D]) {
					if(A == E || B == E || C == E || D == E) {
						continue;
					}
					System.out.println(1);
					System.exit(0);
				}
			}
		}
		System.out.println(0);
	}
}