
작성자 : 연세대학교 기계공학과 김태한
Prior Knowledge
1. What is MAP, MLE?
1) Bayes' rule
두 확률 변수의 사전 확류로가 사후 확률 사이의 관계를 나타내는 정리입니다.
- posterior
- evidence
- prior
- likelihood
A는 관심있는 변수에 해당하며 B는 그러한 A를 추측하기 위한 수단입니다.
2) MAP, MLE
MAP - Maximum A Posterior
MLE - Maximum Likelihood Estimation
여기서 일반적인 모델링이란 확률분포 P의 형태를 정하고(ex. gaussian distribution), 해당 확률분포의 모수를 추정하는 w의 형태(ex. linear regression)를 정하는 것을 말합니다.
여기서 일반적인 linear regression을 기준으로 MAP와 MLE의 차이점에 대해 알아보겠습니다.
Linear regression에서는 P의 분포를 gaussian distribution, 그리고 해당 P의 모수 를 독립변수의 선형결합 즉, 의 형태로 나타내는 모델링을 의미합니다. 이때 w는 를 말합니다.
-
MLE
Likelihood 즉 우도를 최대화 하는 방식으로 변수 X와 y의 관계를 찾아가는 방법입니다.
Convex function을 만들기 위하여 negative log likelihood의 최솟값을 찾아가는 형태로 학습이 이루어지게 됩니다.
이때 negative log likelihood는 에 해당이 되고, 확률분포 는 로 표현됩니다.
Target variable인 y가 일반적으로 연속적인 하나의 값이므로 는 상수값이 되고 는 MSE(mean square error)와 동일한 값이 됩니다.
따라서 negative log likelihood를 하게되면 지수항에 해당하는 MSE부분이 유도되어 linear regression의 objective function은 MSE가 됩니다. -
MAP
Posterior 즉 사후확률분포를 최대로 하는 방식으로 변수 X와 y의 관계를 찾아가는 방법입니다.
여기서 말하는 사후분포에 해당하는 변수는 y가 아닌 y와 X의 관계를 나타내어주는 w를 말하며 따라서 식의 형태는 bayes' rule에 의하여 다음과 같습니다.
여기서 evidence에 해당하는 분모부분은 w가 없으므로 w에 영향을 받지 않는 값으로 상수 취급을 할 수 있으며 해당 값은 전체확률의 법칙을 이용하면 구할 수 있습니다.
이제 분자부분만 계산하면 되는데 위의 MLE에서와 마찮가지로 는 gaussian distribution으로 형태를 정하므로 우리에게 필요한 것은 의 형태만이 남게 됩니다. 따라서 이를 한번 standard normal distribution으로 가정해 보겠습니다.
MLE와 마찮가지로 convex function을 만들어준 후 이를 optimization하기 위하여 negative log posterior를 구하여 보면 가 됩니다. 이때 로그의 성질에 의하여 해당 식은 으로 나뉘어 질 수 있으며 앞의 부분은 MLE와 마찮가지로 MSE값이 됩니다. 이때 뒷부분의 의 경우 standard normal distribution으로 가정하였으므로 이를 풀어주면 의 형태가 됩니다.
이를 다시 보게되면 MSE+의 형태로 우리가 일반적으로 알고있는 ridge regularization인 것을 알 수 있습니다.
즉 MLE는 MAP의 를 uniform distribution이라는 조건의 특수한 케이스 임을 알 수 있습니다. 따라서 모델링을 하여 y를 추정하는 것은 결국 내가 가지고 있는 train set을 얼마나 잘 맞추는 것이 아니라 trains set을 근거로 y와 X의 올바른 관계를 도출하는 것이므로 를 안다면 이를 이용한 MAP로 접근하는 것이 올바른 방법입니다. 하지만 대부분의 경우 를 알지 못하는 경우이므로 어쩔 수 없이 uniform distribution으로 가정한 후 MLE로 학습을 진행하게 됩니다.
2. Kullback Leibler Divergence
1) Information Theory
정보의 가치의 정도를 측정하기 위한 응용수학의 한 갈래
정보의 성질 3가지
1) 자주 발생하는 사건은 낮은 정보량을 가진다.
2) 독립사건은 추가적인 정보량을 가진다 - 정보량이 더해진다.
ex) 투빅이는 사실 여우입니다....!?!?!?
 이건 뻥이지만 만약 투빅이가 진짜 여우였다면 이건 되게 놀라운 사실이겠죠?
따라서 높은 정보량을 가진 정보가 됩니다.
이건 뻥이지만 만약 투빅이가 진짜 여우였다면 이건 되게 놀라운 사실이겠죠?
따라서 높은 정보량을 가진 정보가 됩니다.
이를 수학적인 값으로 표현을 하게 되면 특정 사건이 일어날 확률을 라고 하면 해당 사건의 정보량은 이 됩니다.
2) Kullback Leibler Divergence
이러한 정보량 를 토대로 기댓값을 구하게 되면 그것이 바로 엔트로피(entropy) 값이 됩니다.
이를 토대로 P(X)의 정보량을 다른 확률분포 Q(X)에 대해 기댓값을 구하면 cross entropy를 구할 수 있습니다.
그리고 마지막으로 이러한 cross entropy와 entropy간의 차이가 바로 kullback leibler divergence값이 됩니다.
이러한 kullback leibler divergence값은 P와Q라는 분포의 차이를 나타내주는 지표로 다음의 두 가지 특징이 있습니다.
- 이므로 거리 값이 아니다.
- 항상 0보다 크거나 같다. by jensen's inequality
VAE
1. VAE와 AE?
AE(Auto Encoder): 단순히 차원을 축소하는 것이 목적입니다.
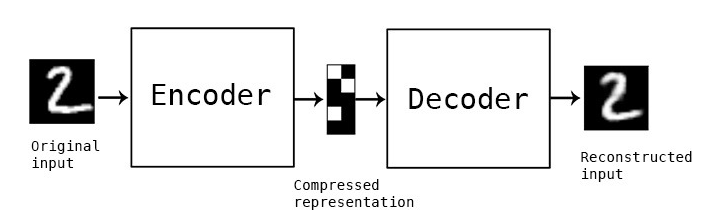
input 변수 X에 대하여 label 값인 y를 예측하는 모델에서 label 값인 y와 X가 같은 값을 가지게 되었을 때 neural network 도중의 hidden variable값이 label인 y(즉 X)에 대한 정보를 담고있다는 점을 토대로 차원을 축소하는 방법입니다. MLE와 유사합니다.
VAE(Variational Auto Encoder): AE와 마찮가지로 label 값과 input 값이 같은 것과 더불어 축소된 차원 값인 latent vector의 분포를 가정하고 해당 가정된 분포의 형태내에서 해당 모델이 label을 잘 맞추도록 학습하는 방법입니다. MAP와 유사합니다.
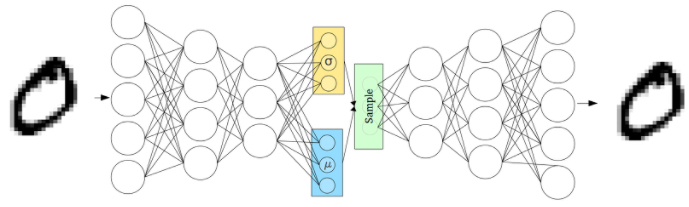
이러한 VAE가 AE와 다르게 가질 수 있는 장점은 아래의 그림으로 알 수 있습니다.

위의 그림에서 (b)그림은 (a)의 일부분 값이 손실된 그림이고 (c)그림은 (a)그림을 한 픽셀시 오른쪽으로 이동한 그림입니다. 이때 MSE값을 (a)를 기준으로 (b)와 (c)에 대해 구하여 보면 숫자 2의 모습은 (c)가 더 유사함에도 불구하고 (b)의 MSE값이 더 작게 나옵니다. 이러한 문제로 인하여 AE는 latent vector의 값이 변화하였을 때 (b)그림이 나올 확률이 높지만 VAE의 경우 latent vector의 분포안에서 특징을 추출하게되는 성질이 있어 (c)가 나올 확률이 상대적으로 AE보다 높아집니다.
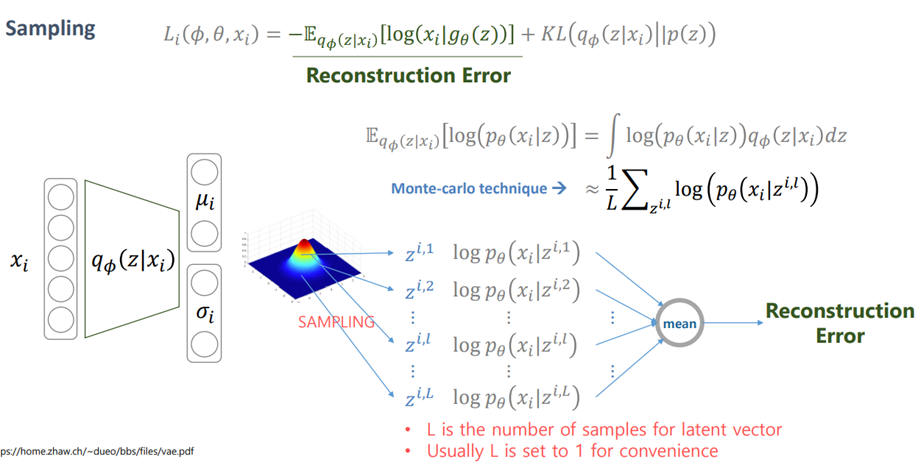
2. ELBO Loss
ELBO Loss 즉 evidence lower bound loss는 VAE의 loss function입니다.
이는 다음의 유도과정을 통해 유도가 됩니다.

여기서 의 ELBO부분(빨간색)과 KL(파란색) 부분으로 나뉘어 지게 되는데 이때 파란색 부분은 실제로는 구하려면 한번 gradient를 update하는데 많은 계산을 하게되어 실질적으로 구하기 어려우므로 ELBO부분의 loss function을 이용하여 학습이 이루어집니다. 이때 실제값을 구할 수는 없지만 최저 한도는 계산이 가능하므로 이를 높여 optimization에 근사하게 됩니다.

그리고 그러한 ELBO Loss function은 위의 식으로 최종 계산됩니다.
여기서 regularization부분의 경우 gaussian distribution간의 KL값은 풀어보면 어느정도 간단하게 정리가 되는 것을 볼 수 있습니다.

또한 reconstruction부분의 경우 continuous variable이면 gaussian, discrete variable이면 cross entropy가 되는 것을 볼 수 있습니다.
3. Mnist training result review
Tensorflow 2.0 공식 홈페이지에서 제공하고있는 VAE 샘플 코드를 통해 학습을 한 결과입니다.

이때 VAE는 사전에 정해둔 분포에 복원시키는 데이터의 특징이 투영되므로 가장 평균적으로 잘 복원시키는 이미지가 gaussian distribution의 평균에 위치하도록 학습이 진행되게 됩니다.
아래의 그림은 mnist training dataset 6000장의 이미지들을 모두 더한후 평균을 취한 이미지로써 학습하여 나타낸 위의 그림의 한 가운데 그림과 유사해 보이는 것을 알 수 있습니다.
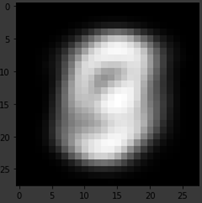
이를 좀더 수치화 하여 각 이미지들과의 차이의 평균을 나타내면 아래의 값처럼 나오게 되고 가운데 즉 평균에 가까울 수록 그 값이 작아짐을 볼 수 있습니다.

따라서 결국 VAE도 학습시 네트워크보다는 train dataset이 얼마나 내가 내포시키고 싶은 특징을 가지느냐에 따라 성능이 굉장히 차이가 나게 됩니다.
AAE & CVAE
1. AAE
기존 VAE의 구할 수 없던 KL divergence값을 GAN의 discriminator를 이용하여 찾아가도록 하는 방법입니다. 기본적인 네트워크의 구성은 아래의 그림과 같습니다.
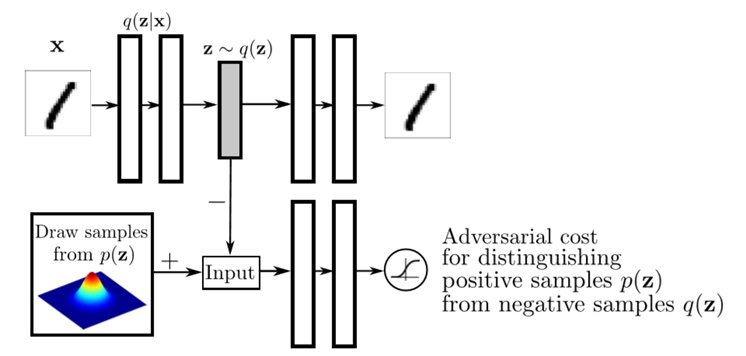
2. CVAE
함축시키고 싶은 정보가 discrete한 class로 label되어 질 수 있다면 이를 이용하여 해당 특징을 학습시키는 방법으로 네트워크의 구조는 다음과 같습니다.
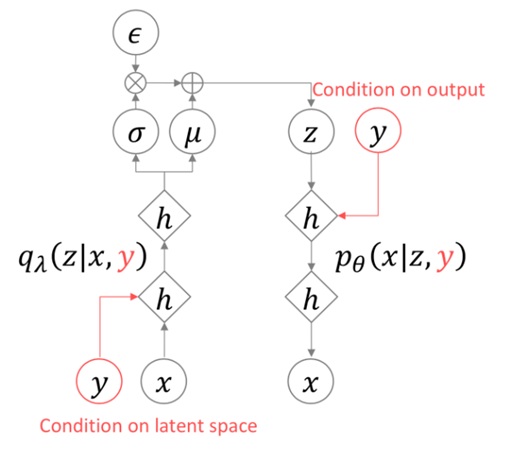
Reference
13개의 댓글
투빅스 14기 박준영:
이번 강의는 VAE에 관한 것으로, 투빅스 12기 김태한님이 진행해주셨습니다.
사전지식으로 MLE, MAP를 짚어 주시고 VAE와 AE의 차이점, VAE의 loss인 ElBO loss 유도과정을 설명해주셔서 VAE를 하나하나 다 해부해 볼 수 있었습니다.
세미나에서 인상 깊었던 파트는
-
AE(오토인코더)는 차원을 줄이는 것이 목적이라 데이터가 생성된 확률분포에는 관심이 없다. 하지만 VAE의 목적은 축소된 latent vector의 분포를 가정하여 latent vector에서 sample을 뽑아 새로운 x를 만들어 내는 것이 목적이다. 그리고 형태가 AE와 비슷해서 VAE라고 이름이 붙여졌다. AE, VAE의 차이점을 통해 VAE가 왜 generation model인지와 VAE의 사용이유를 알게 되었습니다.
-
VAE loss function은 KL, ElBo부분으로 나누어지는데 KL부분은 연산량이 많아 구하기 어려우므로 가우시안 분포를 조건으로 하여 계산하기 쉽게 만들었다는 점. 그리고 negative loglikelihood인 Elbo부분의 값을 최대화하여 Loss를 최소화 시키는 최적화과정을 진행한다는 점, ELBO부분은 연속적이면 가우시안 분포, 이산적이면 cross entropy가 된다는 점이 인상 깊었습니다.
-
VAE는 사전에 정의한 분포를 따라 데이터를 생성하기 때문에 가장 특징을 잘 잡아 복원시키는 이미지가 가우시안 분포의 평균에 위치하도록 학습이 진행되어 학습 시 네트워크보다 train dataset의 특징에 따라 성능이 차이가 난다는 점도 인상깊은 부분이었습니다.
김태한님이 VAE를 원리부터 차근차근 설명을 잘해주어서 generation model의 기반을 잘 닦을 수 있었던 강의였던 것 같습니다.
투빅스 14기 한유진 :
- MAP(Maximum A Posteriori)와 MLE(Maximum Likelihood Estimation)의 차이를 확실하게 알 수 있어서 좋았습니다. MAP는 P(w)의 분포를 가정하고 가는 것이라면, MLE는 그 분포를 uniform distribution으로 주는 MAP의 특수한 케이스입니다. y를 추정하는 것은 x,y의 올바른 관계식을 찾아내는 것이므로 P(w)를 안다면 MAP로, 모른다면 uniform distribution으로 가정한 후 MLE로 학습을 진행하는 것이라고 합니다. 익히 알고있는 MSE가 MLE에서 유도되어서 나왔다는 점, Ridge, Lasso는 MAP에서 나왔다는 점들이 흥미로웠습니다.
- AE와 VAE는 비슷한 구조이지만, 그 구조가 된 이유가 다르고 목적 또한 다릅니다. AE는 manifold learning이 목적이기에 앞단을 위해 뒷단이 붙은것이라면, VAE는 새로운 데이터생성이 목적이기에 뒷단을 위해 앞단이 붙은 것 입니다. VAE는 loss function으로 ELBO Loss를 사용합니다. log(P(X))는 ELBO와 KL로 이루어져있는데 KL을 최소화하는 파이값을 찾으면 되지만 P(z|x)를 모르기 때문에 ELBO를 최대화하는 파이값을 찾는쪽으로 학습이 진행됩니다.
- VAE의 latent vector가 가우시안이 아니라면 loss function의 계산이 어려워지는 단점을 보완하기 위해서 AAE를 사용할 수 있습니다. 이에 대한 활용으로 이미지에 대한 label을 준다던지, y의 class정보에 글씨 두께, 기울어짐과 같은 style정보를 주면 결과가 더 잘나온다고 합니다. 다만, dataset이 좋다는 가정하입니다.
- 축소시키고 싶은 data가 label된다는 것을 이용한 CVAE 구조도 있습니다. 이는 기존의 VAE의 loss function에서 y만 추가하여 조건부 확률로 바꾸기만 하면 된다고 합니다.
VAE를 이해하기위한 사전지식들과 VAE, AAE,CVAE 까지 배워볼수 있었던 유익한 강의였습니다! 감사합니다!
투빅스 14기 김상현:
이번 강의는 VAE에 대한 것으로, 김태한님께서 진행해주셨습니다.
사전 지식인 MAP, MLE 및 KL Divergence을 통해 VAE의 원리를 알 수 있었습니다. 추가로 AAE와 CVAE에 대해 알 수 있었습니다.
-AE는 MLE와 유사하다는 점과 VAE는 MAP와 유사하다는 점을 통해 둘의 차이와 VAE에 대한 전반적인 이해를 하는데 도움이 됐습니다.
-VAE의 목적은 p(x)를 최대화입니다. 여기서 log(p(x))를 ELBO와 KL 부분으로 나눌 수 있는데 KL부분을 계산하기 어렵습니다. 따라서 ELBO를 최대화하는 방향으로 학습을 진행합니다. ELBO 부분은 reconstruction error와 regularization을 나눌 수 있고, 이를 이용해서 손실함수를 정의해 최적화를 진행합니다.
-Regularization은 KL divergence의 계산 방법에 따라 쉽게 계산할 수 있습니다. 또한 Reconstruction error은 MLE와 같이 가정한 분포에 따라 cross entropy 또는 MSE로 계산할 수 있습니다.
-Gan의 discriminator를 이용해서 latent vector의 분포를 결정할 수 있는 AAE를 알 수 있었고, CVAE를 이용한 conditional한 생성모델을 알 수 있었습니다
사전지식부터 VAE의 advanced 버전까지 차근차근 설명해주어서 VAE를 이해하는데 큰 도움이 되었습니다.
유익한 강의 감사합니다!
투빅스 13기 신민정:
이번 VAE강의는 12기 김태한님께서 진행해주셨습니다.
-
MLE는 Likelihood를 최대화하는 방식으로 x와 y의 관계(w)를 찾아가는 것이고, MAP는 Posterior을 최대화하는 방식으로 x와 y의 관계를 찾아갑니다. MLE는 MAP의 P(w)를 uniform distribution이라는 조건의 특수한 케이스이고, P(w)를 안다면 MAP를 이용하고 그렇지 않다면 MLE를 이용합니다. (MLE는 MAP의 특수한 케이스) (대부분의 경우 P(w)를 알지 못하므로 MLE이용) MAP는 MLE보다 train dataset에 덜 의존합니다. Linear regression을 예로들어 설명해주셨습니다. 특정 독립변수의 설명력을 제한하는 Ridge regression이 MAP에서 나온것임을 알 수 있었습니다.
-
KL Divergence는 두 확률분포 간의 차이를 나타냅니다. KL=0 이면 분포가 같은것입니다.
-
VAE의 loss인 ELBO loss에 대해 알아보았습니다. 우리가 최대화하고 싶은 log(P(x))는 ELOB항과 KL항으로 이루어져 있는데, KL항을 실제로 구하기 위해서는 gradient를 update하는데 많은 계산량이 요구되기 때문에, ELBO를 최대화합니다. log(P(x))의 ELBO항은 Reconstruction error항과 Regularization(KL)으로 나뉘게됩니다. Reconstruction error는 연속형 변수일 때는 Gaussian(identity covariance일 때 squared error), 이산형 변수일 때는 Cross entropy으로 계산되고, Regularization항은 수식으로 계산가능합니다.
-
VAE을 사용하기 위해서는 나타내고 싶은 data를 잘 담고있는 data set이 필요합니다.
MAP와 MLE의 차이와 VAE Loss, AAE,CVAE까지 배울 수 있는 유익한 강의였습니다. 알찬강의 정말 감사드립니다. [국대태한의 VAE 띵강의를 들을 수 있어서 영광이었습니다.@v<]
질문] 이활석님의 '오토인코더의 모든것'강의에서 log(p(x)) = ELBO term + KL term이고, KL의 p(z|x)를 모르기 때문에 ELBO를 최대화한다고 하셨는데, 강의자님께서 말씀해주신 "KL항을 실제로 구하기 위해서는 gradient를 update하는데 많은 계산량이 요구되기 때문에, ELBO를 최대화"한다는 내용과 같은 맥락인지 궁금합니다.
투빅스 11기 이도연:
VAE를 이해하기 위해 필요한 사전지식부터 오늘의 주제였던 VAE, 그리고 AAE, CVAE까지 전반적인 흐름을 따라가며 이해하는 매우 유익한 강의였습니다! 감사합니다.
- MAP(Maximum A Posteriori), MLE(Maximum Likelihood Estimation)
베이즈 이론 Posterior ∝ Prior * Likelihood 에서 MAP를 구하는 것이 가장 이상적이지만, Prior를 알기란 거의 불가능하기 때문에 MAP의 일부분인 MLE를 사용해 근사한다. 참고로 우리가 Regularization의 방법으로 알고있던 Ridge도 MAP로부터 유도할 수 있다. MLE는 MAP에서 Prior를 Uniform Distribution으로 가정한 특수한 경우라고 생각할 수 있다. - VAE(Variational AutoEncoder) vs AE(AutoEncoder)
AE는 차원을 축소(manifold learning)하는게 목적이고, VAE는 새로운 데이터를 생성하는게 목적이다. AE는 Encoder에 VAE는 Decoder에 집중한다. - VAE의 Decoder에서는 latent vector z로부터 새로운 데이터(x)를 생성하는데 이 z를 고르는 이상적인 sampling 함수 p(z|x)가 있다고 했을 때, 이 p(z|x)를 구하기 어렵다. 그래서 우리가 알고있는 분포(q(z))의 파라미터 값을 조정해 p(z|x)와 유사하게 근사시킨다.(변분추론, Variational Inference) 이 때, p(z|x)와 q(z) 사이의 KL Divergence(두 확률 분포 사이의 거리)를 계산해 줄어드는 방향으로 학습하고자 한다.
- 우리의 목적은 log(p(x))를 최대화 하는 것, 즉 ELBO를 최대화 하는 것, KL을 최소화 하는 것 L=−Ez∼q(z|x)[logp(x|z)]+DKL(q(z|x)||p(z)) 이 함수를 최소화하는게 학습의 목표. 첫번째 항은 reconstruction loss로 현재 샘플링 된 z에 대한 negative log likelihood, 두번째 항은 KL Divergence Regularization으로 샘플링 된 z에 대한 추가 조건을 의미한다.
앞으로 배우게 될 Generative Model들이 기대된다!!
투빅스 14기 정재윤:
생성모델 세미나의 첫 번째 강의는 투빅스 12기 김태한님께서 진행해주셨습니다.
-
처음으로 인상깊었던 부분은 MLE와 MAP를 설명해주시는 부분이었습니다. MLE와 MAP는 딥러닝에서 자주 등장하는 용어 중 하나입니다. MLE는 주어진 파라미터를 기반으로 데이터의 likelihood를 최대화 시킬 때 사용합니다. 그리고 이런 MLE보다 더 이상적인 척도 값이 MAP이지만 일반적으로 이 MLE로 모델을 학습시키는데 사용합니다. 이는 저희가 정확히 사전분포를 모르기 때문입니다.
-
MAP를 사용하여 linear regression에서 ridge regression을 유도하는 것이 굉장히 인상 깊었습니다.
-
정보이론을 바탕으로 Kullback Leibler Divergence를 설명해주셨습니다. 정보이론부터 출발하여 정보의 값을 구합니다. 정보량의 평균인 entropy와 q분포를 통해 구한 정보량을 p분포의 분류 전략에 사용하는 척도인 cross entropy를 구하여 Kullback Leibler Divergence를 p분포와 q분포의 차이를 나타내는 지표로 나타냈습니다. (즉, 거리 값이 아니라는 것이 중요합니다.)
-
AE와 VAE의 구조는 굉장히 유사해보이지만 그 근간은 다릅니다. 특히 VAE의 경우, 베이지안 통계를 바탕으로 학습을 진행합니다. x라는 target data가 주어지면 이를 바탕으로 우리는 z의 분포를 찾아야 합니다. 그러나 대부분 이 분포는 찾을 수 가 없으므로 우리가 익숙한 확률분포를 설정하여 파라미터를 찾아가며 이를 찾아가는 것입니다.
-
실제 코드를 통해 VAE의 결과값을 확인해봤으며, 특히 유사도를 나타내는 결과를 구한 것이 굉장히 인상깊었습니다.
-
마지막으로 AAE와 CVAE의 구조를 가볍게 훑어보고, 이를 코드를 돌려 결과로 보여줌으로써 좀 더 쉽게 구조와 그 장단점을 이해할 수 있었습니다.
생성모델을 공부함에 있어 꼭 필요한 기본이 되는 용어와 개념을 확립하고 이를 심도있게 생각할 수 있게 만들어주신 굉장한 강의였습니다. 감사합니다!
투빅스 14기 박지은:
- VAE를 이해하는 데 필요한 사전지식을 잘 알려주셔서 더 도움이 되었습니다. 먼저 liner regression을 기준으로 MLE는 likelihood를 최대화 하는 방식으로 negative log likelihood를 하면 목적함수는 MSE가 됩니다. 반면 MAP는 posterior를 최대화하는 방식으로 목적함수는 MSE에 standard normal distribution을 더한 ridge 정규화가 됩니다. 실제로는 P(w)를 알 수 없기 때문에 uniform distribution을 전제하고 MLE를 통해 학습하게 됩니다. Kullback Leibler Divergence는 정보량을 토대로 계산한 cross entropy와 entropy 간의 차이로 P와 Q의 분포의 차이를 알려줍니다.
- VAE는 AE와 비슷한 학습 방법을 가지고 있지만, latent vector의 분포 안에서 특징을 추출하게 되어 AE보다 더 현실적인 손실을 계산할 수 있다고 합니다. 이는 정보를 유지하며 단순히 차원을 축소하는 AE와 달리 VAE는 새 데이터를 생성하기 때문입니다.
- ELBO loss는 VAE의 loss function으로 log(P(X))는 ELBO 부분과 KL 부분으로 나뉘는데, KL은 계산량이 많아 실제로 구하기 어려워 ELBO loss를 이용하여 학습합니다. AAE는 이렇게 구할 수 없던 KL divergence를 GAN을 활용하여 찾아가는 방법입니다. 이 밖에도 latent vector가 가우시안 분포가 아닐 때도 사용할 수 있습니다.
VAE를 이해하기 위해 필요한 사전지식부터 다양한 활용까지 친절하게 설명해주셔서 정말 유익한 강의였습니다. 또한 시각 자료와 수식에 대한 설명이 풍부하여 이해에 더 도움이 되었습니다. 정말 감사합니다!
투빅스 14기 김민경
- MLE는 Likelihood(우도)를 maximize하는 방식으로 변수 X와 y의 관계를 찾아가는 방법이고, MAP은 Posterior(사후확률분포)를 maximize하는 방식으로 변수 X와 y의 관계를 찾아가는 방법이다. 만약 우리가 prior를 알고 있다면 MAP는 이상적인 척도 값이 되지만 현실적으로는 거의 불가능하므로 trainset에 의존적인 MLE를 사용하게 된다. 이때, prior를 uniform distribution으로 가정하면 MLE는 MAP와 같은 문제가 되므로 이 가정 하에 MLE로 학습을 진행한다.
- 정보이론이란 정보의 가치 정도를 측정하는 분야이다. 이 정보의 양을 표현하는 개념이 엔트로피이다. KL-Divergence는 p와 q의 cross entropy에서 p의 entropy를 뺀 값이다. 즉, 확률분포 p와 확률분포 q의 차이를 나타내는 지표로써 두 확률 분포의 다름을 설명할 수 있다. 주의할 점은 KL-Divergence가 항상 0 이상이기 때문에 거리 값이 아니라는 것이다.
Auto Encoder는 단순히 차원을 축소하는 것이 목적인 신경망이고, VAE는 어떤 input을 넣었을 때 그 input의 차원을 축소하면서 가장 잘 표현하는 latent vector의 분포를 가정하고 이 가정된 분포에서 label을 잘 맞추도록 학습하는 방법이다. 강의에서 MAP와 유사하다고 하셔서 처음엔 이해가 안 됐는데 좀 더 찾아보니, training data 각 z에 대해서 p(X)를 최대화 시키는 것이 목표이므로 특징들 z가 주어졌을 때 그때의 data X의 확률을 학습하여 아예 p(X|z) 자체를 학습한다고 생각하면 되니까 MAP와 유사하다고 한 것이다. - p(X)의 최댓값을 구하기 위해 log를 씌우면 ELBO부분과 KL부분으로 나뉘어지게 된다. 계산의 복잡성으로 ELBO부분을 VAE의 loss function으로 이용하여 학습을 하는 것이다. 계산의 복잡성으로 구할 수 없었던 KL부분을 GAN의 discriminator으로 찾을 수 있게 하는 방법이 AAE이다. MAE와 비교하여 AAE는 좀 더 prior에 가깝게 학습이 된다는 장점이 있다. CVAE는 VAE의 encoder와 decoder에 함축시키고 싶은 정보의 label 정보를 알고 있으면 제공해서 학습하는 방법이다.
- VAE를 이해하기 위한 기본 용어들과 자세한 개념들까지 차근차근 설명해주셔서 정말 도움이 되었던 강의였습니다. 감사합니다:)







투빅스 13기 이예지:
이번 강의는 VAE에 대한 것으로, 김태한님께서 진행해주셨습니다.
VAE 이해에 필요한 분포가정 후 목적함수를 유도하는데 필요한 개념과 정보이론에 사용되는 정보량의 개념과 KL divergence 다뤘고, AE와 VAE의 등장배경과 차이점, 목적함수 유도에 대해 알 수 있었습니다.
VAE의 전반적인 설명과 설명에 필요한 여러 개념들을 정리해줘서 매우 유익했습니다.
감사합니다 :)