
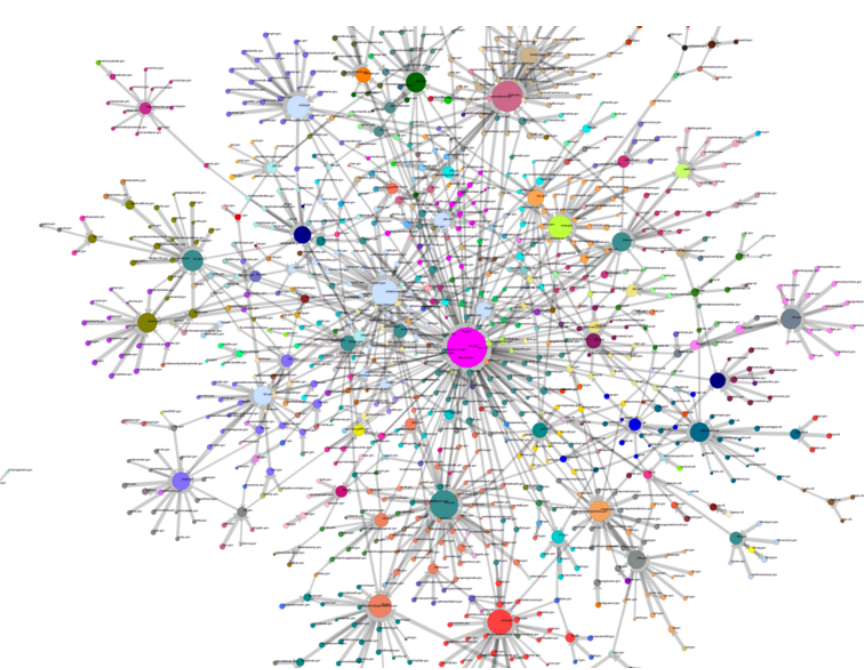
Web as as Graph
Structure of the web
- 인터넷 웹을 그래프로 생각해보자
- nodes = web pages
- edges = hyperlinks
- 웹 페이지 내부에서 외부 웹 페이지로 링크를 달면 edge가 생긴다고 볼 수 있다
- Web is a Directed Graph
- web grpah를 보면 directed graph인 것을 알 수 있다
- 이렇게 연결된 링크를 BFS로 크롤링을 하면 Google의 웹페이지를 몽땅 훑어볼 수 있다
What does the web look like?
- 인터넷 웹을 그래프로 만들었으면 어떻게 생겼을까?
- Web as a directed graph [Broder et al, 2000]
- In(v): node v가 directed edge를 따라서 도달할 수 있는 다른 node의 set
- Out(v): directed edge를 따라서 node v에 도달할 수 있는 다른 node의 set
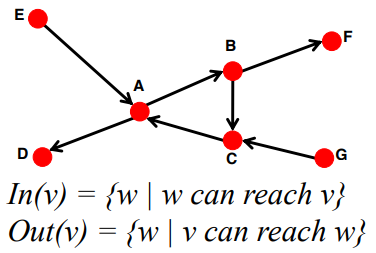
-
Two types of directed graphs
-
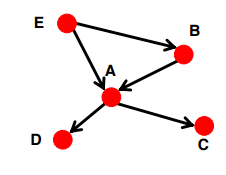
Strongly connected: 어느 node에서든 다른 node에 도달할 수 있음
In(A) = Out(A) = {A, B, C, D, E}
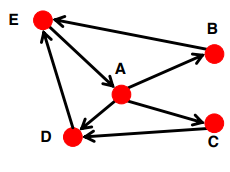
-
Directed Acyclic Graph(DAG): cycle이 없음. 노드 v에서 u에 도달할 수 있다고해도 u에서 v로 갈 수 없을 수도 있음
-
모든 directeed graph(e.g. web)은 이 2가지 타입에 속한다!
-
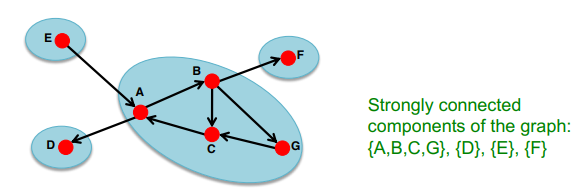
Strongly Connected Component(SCC)
-
SCC 내에서 어느 noed에서 출발하든 다른 node에 도달할 수 있음(strongly connected)
-
현재 SCC를 포함한 또 다른 SCC는 존재할 수 없음 → 모든 node는 한 SCC에만 속한다
-
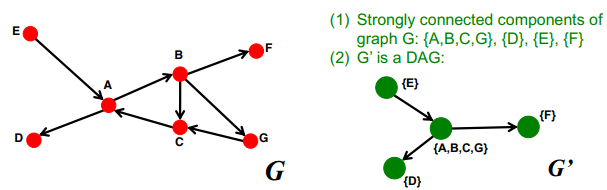
FACT: 모든 directed graph는 SCC의 DAG으로 표현할 수 있다
- SCC는 전체 그래프의 partition이다. partition이라 함은 중복이 없다는 뜻
- 전체 그래프 G를 참고하여 G의 SCC를 G'로 만들 수 있다. 이 때 edge는 G와 G' 모두 동일하게 매핑할 수 있고 G'는 DAG라고 볼 수 있다.
Graph structure of the web
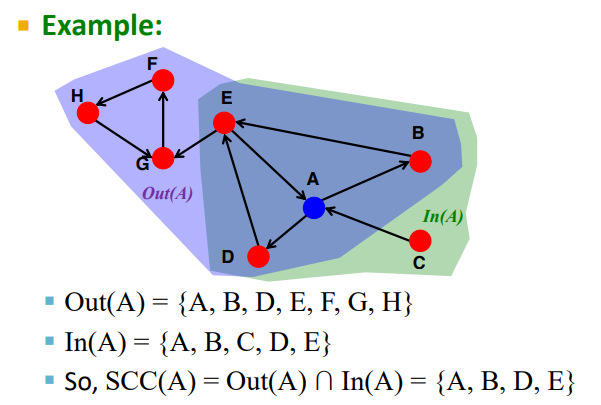
- Computational issue: 현재 node가 어느 SCC에 포함되어있는지 어떻게 알 수 있을까?
- Observation: node v를 포함하는 SCC = Out(v)∩In(v) = Out(v, G)∩Out(v, G')
- Directed version of the web graph
- 웹을 graph로 정의하고 일부 노드에서 시작해서 BFS어디까지 탐색할 수 있을까?
- 결과를 살펴보면 출발 node 노드 비중이 어느 시점을 기준으로 대부분 탐색할 수 있거나 조금 밖에 탐색할 수 없는 경우로 나타났다
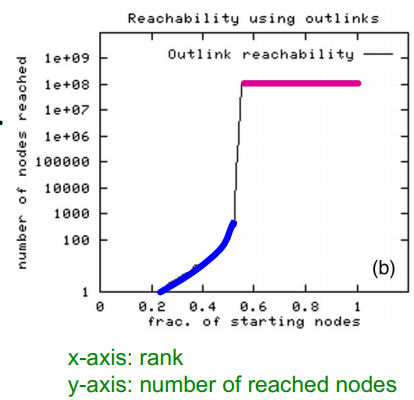
- random node v에 대하여
- Out(v): 1억(전체 node의 50%)
- In(v): 1억(전체 node의 50%)
- 가장 큰 SCC: 5천 6백만(전체 node의 28%)
- 이러한 인사이트를 바탕으로 Bowtie structure를 그릴 수 있다
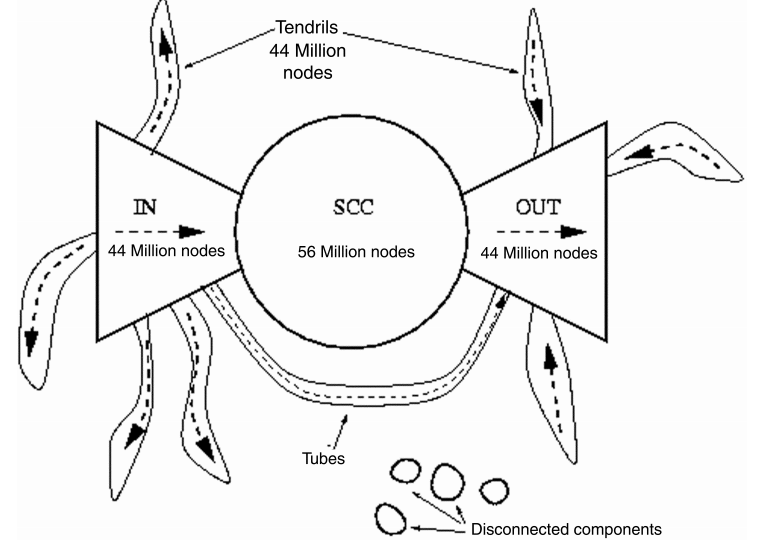
PageRank
- How to organize the web
- made by Google research
Ranking nodes on the graph
- 모든 웹 페이지 각각의 중요성은 저마다 다를 것이다
- 신윤종의 깃헙 vs HuggingFace 깃헙
- 그래서, web graph를 활용하여 rank를 매겨보자
- Link analysis approaches
* PageRank- Personalized PageRank
- Random Walk with Restarts
Link as Votes
- IDEA: link(edge)는 민주주의적으로 투표로 따집시다
- link가 많은 page는 중요도가 높을 것이다!
- In-link를 중요도의 지표로 따져보자
- 신윤종의 깃헙(팔로워 11명) vs HuggingFace 깃헙(Transformers만 해도 star 42만개)
- 모든 in-link가 중요할까?
- 중요한 페이지에서 보낸 link가 다른 link보다 더 중요할 것이다
- Recursive question!
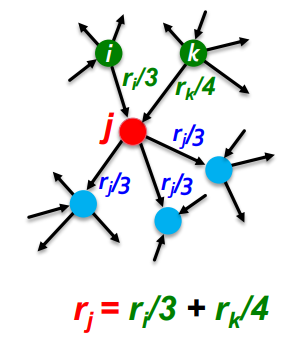
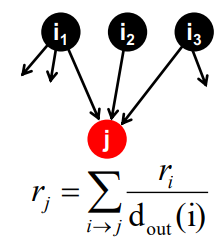
PageRank: The "Flow" Model
- 중요한 페이지에서 보낸 "투표"가 더 가치 있을 것이다
- 각 link는 source page의 중요성 비율이다
- 만약 page i의 중요도 가 out link를 가지고 있을 때, 각 link는 만큼의 vote 가중치를 가진다
- page j의 중요도 는 j의 in-link vote의 합이다
Matrix Formulation
- Stochastic adjacency matrix M
- page j는 out link {d_j}를 가진다고 하자
- 만약 j에서 i로 링크가 연결된다면
- 의 column 하나의 sum은 1이다
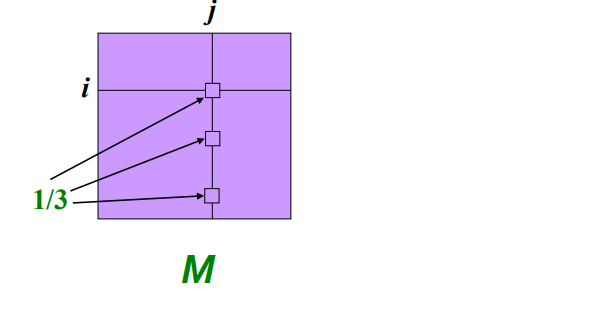
- 의 column 하나의 sum은 1이다
- Rank vector r
- 는 page i의 중요도를 의미한다
- flow equation

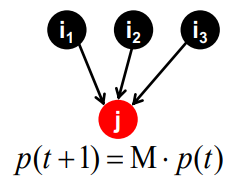
Random walk interpretation
- random web surfer
- 특정 time t에 page i를 서핑하고 있다고 해보자
- 다음 t+1에 uniformly random하게 결정된 out-link를 따라 page j로 이동한다
- 이 과정을 무한히 반복한다
- : 전체 페이지 개수만큼의 벡터로, i째 원소는 time t에서 i에 도달할 확률을 의미한다
- time t+1에 어디에 있을까?
- 균등확률로 랜덤하게 움직여보자
p(t)는 aP = a를 만족하는 stationary distribution 상태이다
- 균등확률로 랜덤하게 움직여보자
- 앞서 배운 rank vector는 인데?
- 따라서 r은 random walk에서 stationary distribution 상태이다
Eigenvector formulation
-
에 따라 rank vector r은 stochastic web matrix M의 eigenvector임을 확인하였다
-
임의의 node u에서 출발해서 random walk를 진행한다고 해보자 수식은
가 된다. -
좀더 풀어서 써보면
-
그럼 우리의 pagerank를 쉽게 뽑을 수 있을 거 같다
-
Power iteration
- Power iteration; simple iterative scheme
- 초기화: where N= # of nodes
- 반복:
- 기저: (L1 norm)
PageRank: how to solve?
- 모든 노드마다 page rank를 초기화한다
- power iteartion으로 수렴할 때까지 반복한다

3 Questions
- 그래서 실제 그래프에서는 수렴하긴 하나?
- 수렴하면 우리가 원하는 모양으로 수렴하나?
- 결과는 합리적인가?
→그러니까 일반적인 상황에서 써먹을 수 있냐구
Problems
- Problem 1) 어떤 페이지는 막다른길이다
- out-link가 없다
- importance의 leakage를 유발한다
- pagerank의 수렴에는 문제가 되지 않지만 pagerank score가 맘에 들지 않을 것이다

- Problem 2) Spider traps
- 모든 out-link가 group에 속해있을 때 모든 importance는 해당 group이 모두 흡수해버린다
- pagerank 수렴에 문제가 생긴다
Solutions
- Spider traps의 해결책: 각 time마다 random sufer는 2가지 선택지가 생긴다
- 확률 β는 link를 그대로 따라갈 확률이다
- 확률 1-β는 연결되어있지 않는 랜덤한 page로 점프할 확률이다
- 일반적으로 β는 0.8~0.9로 설정한다
- Dead ends 해결책:
- Teleports: 막다른 길에 다다른 node에게 다른 node로 연결될 확률은 배분한다
* dead ends node m이 다른 node로 갈 확률의 전체 합은 1이다
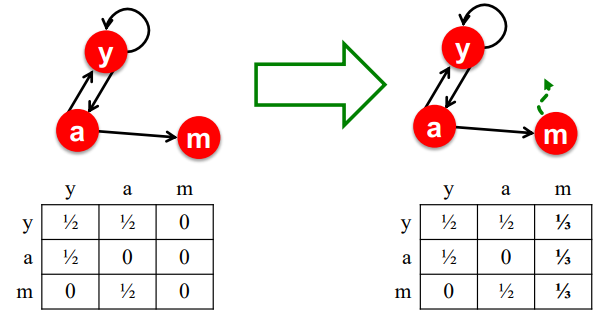
- Teleports: 막다른 길에 다다른 node에게 다른 node로 연결될 확률은 배분한다
Google matrix
- Spider traps를 고려한 Pagerak 수식
- 이 수식은 에 균등확률을 배정하는 전처리를 진행하여 dead ends 문제를 피할 수 있다.
- Google Matrix A
- 여전히 의 재귀적인 문제가 있지만 power iteration을 사용해준다
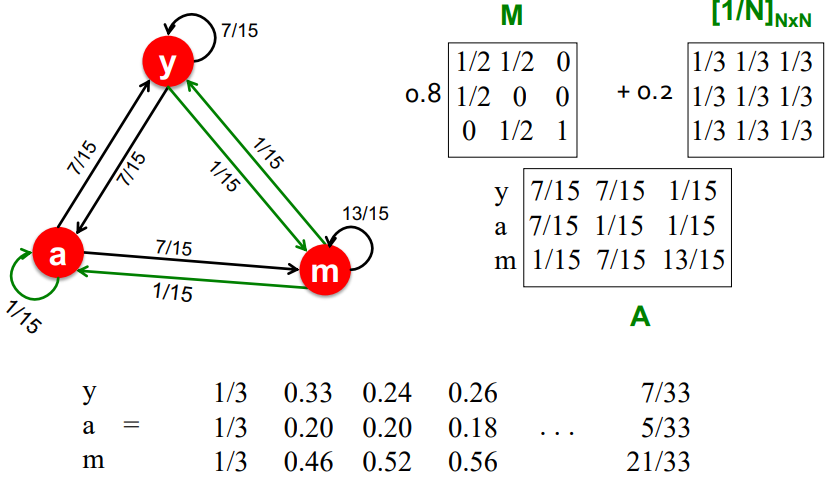
- 여전히 의 재귀적인 문제가 있지만 power iteration을 사용해준다
How do we actually compute PageRank?
Computing PageRank
- N = 10억 page
- 각 entry마다 4byte를 쓴다고하자
- pagerank r이 old, new 2종류가 합해서 8GB가 필요하다
- Google matrix A는 N*N크기이다
- 개수만 해도 ${10}^{18}이다
Sparse Matrix formulation
- 수식을 재정의해보면
- M은 sparse matrix로 dead ends가 없다는 가정하에 10개의 링크가 각 노드마다 달려있다고하면 10N entries가 있다고 볼 수 있다
- 매 반복마다 pagerank 공식에 (1-β)/N의 상수를 각 에 더하면 된다
- 다만 dead-ends가 우려되는 상황이라면 normalize해주자
Complete algorithm
- Input: Graph G and parameter β
- Output: Pagerank vector
- Set
- 수렴할 때까지 반복:
- in-link가 없는 경우에는 0
- leaked pagerank 정보를 더해준다
Node Proximity Measurement
- Bipartite graph에서의 pagerank는?
- 같은 종류끼리는 독립인데?
Proximity on graphs
- personalized pagerank: random walk로 계산해보자
- query nodes가 주어지면 random walk 수행
- restart proba가 주어지면 random walk를 처음부터 수행하게 됨
- 주어진 query nodes들이 가장 많이 방분한 node가 highest proximity를 보인다

1. Web as a Graph
PageRank는 web 환경을, graph 로 표현하여 page 의 중요도를 나타내는 알고리즘입니다.web page 가
node가 되며, hyperlink 는edge가 됩니다.Web as a Directed Graph
web 을 Directed Graph 로 표현할 때, 구성 요소는 다음과 같습니다.
In(v): directed edge를 따라서 node v에 올 수 있는 node setOut(v): node v가 directed edge를 따라서 갈 수 있는 node set모든 Directed Graph 는 아래의 2가지의 경우에 속합니다.
1.
Strongly Connected: 어느 node 에서 출발하든지 다른 node 에 도착할 수 있는 graph2.
Directed Acyclic Graph (DAG): node v에서 u에 도달할 수 있어도, node u에서 v로 갈 수 없을 수도 있는, cycle 이 없는 graphA Strongly Connected Component (SCC)
내부의 모든 node에서 내부의 다른 모든 node로 갈 수 있는 최대 그룹을 말합니다.
모든 directed graph는 SCC 의 DAG 로 표현할 수 있습니다.
SCC를 뭉쳐서 하나의 node 로 보는, G' graph를 만들면, G'는DAG가 됩니다.Graph Structure of the Web
따라서 이러한 directed graph 의 속성을 web 에 적용시키고자 합니다.
SCC 가 node v 를 포함하는지에 대해 계산하고자 할 때,
Out(v) ∩ In(v) 를 계산하면, node v 에 대한 SCC를 알 수 있다는 점에 착안하여
Out(v, G) ∩ Out(v, G') 이라는, graph G 의 방향을 뒤집은 G' 을 통해 SCC(v) 를 계산합니다.
2. PageRank
PageRank는 모든 webpage 가 equally important 할까? 라는 idea로 부터 출발한 알고리즘입니다.위와 같은 flow를 통해 아이디어를 적용한 것이 PageRank 입니다.
Model Flow
importance가 ri 이고, diout-link를 가지고 있을 때, 각link는 ri/di 만큼의 가중치를 가집니다.in-link vote의 합 으로 계산됩니다.Matrix Formulation
M: Stochastic Adjacency Matrixr: Rank VectorFlow Equation
r=M⋅r , 이는 recursive equation 입니다.
(PROCESS) Power Iteration
Initialize: r(0)=[1/N,...,1/N]T각 node 는 균등한 가중치로 시작됩니다.
Iterate: r(t+1)=M⋅r(t)연결된 node 로 부터 가중치를 넘겨받는 과정이 재귀적으로 반복됩니다.
Stop: when ∣r(t+1)−r(t)∣1<ε오차가 특정 값으로 수렴할 때 까지, multiply M 을 반복합니다.
Problems
Flow Equation을 그냥 적용할 시, PageRank 가 수렴하지 않거나, PageRank Score 에 문제가 생기는 경우가 발생합니다.1.
Dead-Ends: out-link 가 존재하지 않아서, importance leakage 를 유발하는 문제2.
Spider Trap: 모든 out-link 가 group 에 속해 있어서, 모든 importance 를 해당 group 이 다 흡수해 버리는 문제Solutions
따라서
Teleports를 통해 이를 해결합니다.1. for Dead Ends : 막다른 길에 다다른 node 에게, 균등한 확률을 배분합니다.
2. for Spider Traps : 각 time step 마다, random surfer 는 β (link 를 그대로 따라갈 확률) or 1−β (random page 로 jump 할 확률) 로 움직입니다.
Google Matrix
위의 두 가지 문제를 해결하기 위해,
Google Matrix: A=β⋅M+(1−β)[1/N]N×N라는, leaked PageRank 에 균등 확률을 배분하는 PageRank equation 을 세워 score 를 계산합니다.
Complete Algoritm
Google Matrix 를 통해 PageRank 를 계산하면, rnew=A⋅rold 을 계속 계산하게 됩니다. 즉, sparse matrix 가 아니라, 1/N 값을 더해서 만든 dense matrix 를 계속 곱해서 계산하기 때문에, N 이 커지면 computation problem 이 발생하게 됩니다.
따라서 Rearrange 한 식으로 PageRank 를 계산합니다.
M 은 sparse matrix 가 되며, 1 step 마다 Sparse matrix 를 곱하고, 그 때마다 1/N 을 따로 더하게 됩니다.
∴rnew=βM⋅rold+(1−β)[1/N]N×N
자세한 건 리뷰 에 적었슴니다 ㅎㅎ 띵강 감사합니다 ~!!