투빅스 NLP 컨퍼런스 때 추출요약 알고리즘으로 썼던 TextRank ..
텍랭의 근간이 되는 PageRank 에 대해 공부해 보기로 한다 ~
Contents
- Web as a Graph
- PageRank
1. Web as a Graph
우리가 열심히 살고 있는 web 환경은 graph 로 표현이 가능하다
nodes= web pagesedges= hyperlinks
42월드 파도타기 하듯이, webpage 에 걸려 있는 hyperlink 를 통해 넘어가고 넘어가며 이동할 수 있다
webpage 가 node 가 되며, webpage 와 webpage 를 이어 주는 hyperlink 가 edge 가 된다
특히 web 은 방향성이 있는 directed graph 로 표현 가능하다!
Web as a directed graph
web 을 directed graph 로 표현했을 때, 구성 요소는 다음과 같다
In(v): directed edge를 따라서 node v에 올 수 있는 node set
ex. In(A) = {A,B,C,E,G}Out(v): node v가 directed edge를 따라서 갈 수 있는 node set
ex. Out(A) = {A,B,C,D,F}
Two types of directed graphs
모든 directed graph 는 아래의 2가지 경우에 속한다
- Strongly Connected
Any node can reach any node via a directed path
어느 node 에서 출발하든지 다른 node 에 도착할 수 있는 graph
- Directed Acyclic Graph (DAG)
Has no cycles : if u can reach v, then v cannot reach u
node v에서 u에 도달할 수 있어도, node u에서 v로 갈 수 없을 수도 있는, cycle 이 없는 graph
A Strongly Connected Component (SCC)
- Every pair of nodes in S can reach each other
(= SCC내의 임의의 두 node u, v 사이의 u → v 경로와, v → u 경로가 항상 존재한다.) - There is no larger set containing S with this property
현재 SCC를 포함한 더 큰 집합의 또 다른 SCC는 존재할 수 없다.
(= SCC 내의 임의의 node u와, 외부의 임의의 node v 사이에, u → v 경로와, v → u 경로가 동시에 존재하는 경우는 없다.)
즉, SCC 는 내부의 모든 node에서 내부의 다른 모든 node로 갈 수 있는 최대 그룹을 말한다
FACT : Every directed graph is a DAG on its SCCs
모든 directed graph는 SCC 의 DAG 로 표현할 수 있다!
SCC (={A,B,C,G}) 를 뭉쳐서 하나의 node 로 보는, G' graph를 만들면, G'는 DAG 가 된다 ~
Graph Structure of the Web
그래서 이러한 directed graph 의 속성을 web에 적용하고자 하는데 ...
SCC 가 node v 를 포함하는지에 대해 계산하고자 하면.. computation problem 생겨서 머리가 아프다
따라서 Out(v) In(v) 를 계산하면, node v 에 대한 SCC를 알 수 있다는 점에 착안하여
Out(v, G) Out(v, G') 이라는, graph G 의 방향을 뒤집은 G' 을 통해 SCC(v) 를 계산한다 ~
- Out(A) = {A,B,D,E,F,G,H}
- In(A) = {A,B,C,D,E}
따라서, SCC(A) = Out(A) In(A) = {A,B,D,E}
Bowetie Structure of the Web
web 에서 BFS 를 통해 연결 되어 있는 web(node) 를 탐색하면,
아주 조금 탐색해 버리거나, 완전 다 탐색해 버리는 극단적인 경우로 나뉘어진다
따라서 random node v 에서 계산한 In(v), Out(v) 를 통해 SCC(v) 를 그려보면,
아래와 같은 Bowtie Structure 가 나타남을 알 수 있다
2. PageRank
PageRank 는 .. 모든 webpage 가 equally important 할까? 라는 idea로 부터 출발한 알고리즘이다 ~
윤종이가 얘기해 준 찰떡같은 예시를 보면,
1. 모든 웹 페이지의 중요도는 다르다 (ex. 나의 github vs HuggingFace github... ㅠㅠ)
2. Link Analysis : web graph 를 통해 ranking 을 매겨서, 중요도를 파악해 보자!
3. idea : link 가 많은 webpage 는 중요도가 높을 것이다
4. 특히, in-link 를 중요도의 지표로 따져 본다
5. 중요한 페이지에서 보낸 link가 다른 link보다 더 중요할 것이다
(ex. 친구들에게서 온 dm vs 인기 짱짱 연예인으로부터 온 dm)
위와 같은 flow를 통해 아이디어를 적용한 것이 PageRank ~
즉, 🧐 너의 중요도는 뭐야 ~? → 🙄 친구한테 물어봐!
PageRank : The "Flow" Model
중요한 페이지에서 보낸 투표가 더 가치 있을 것이다!
- page i 의
importance가 이고,out-link를 가지고 있을 때, 각link는 만큼의 가중치를 가진다 - page j 의 importance 는
in-link vote의 합!
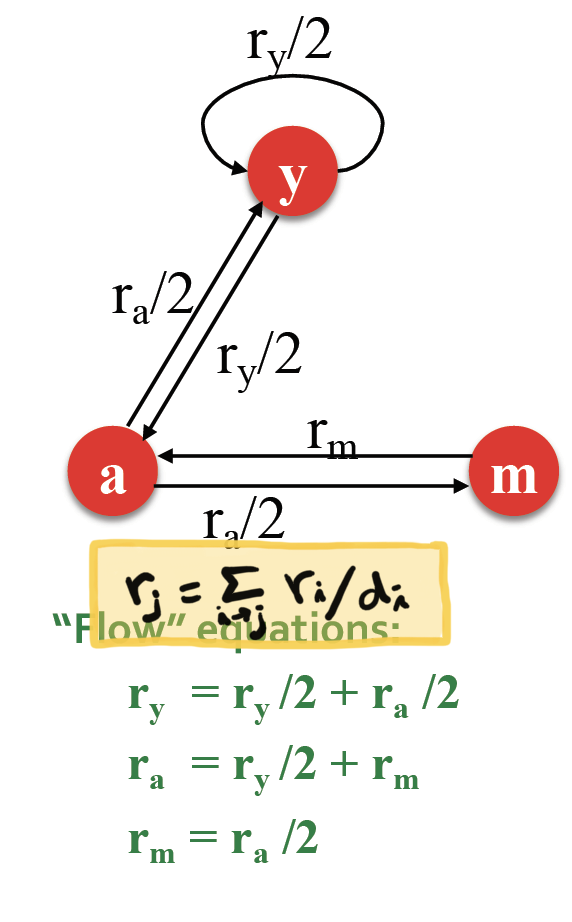
3 equations & 3 unknowns 이므로 방정식을 풀 수 있다 ~
Matrix Formulation
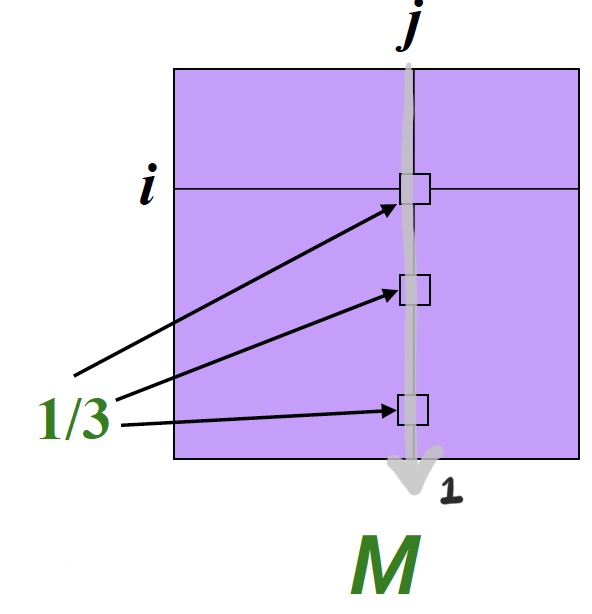
M : Stochastic Adjacency Matrix
- j → i 라는 link 가 존재한다면,
- 은 column stochastic matrix 로, 화살표 방향으로 값을 다 더하면 1이 된다
r : Rank Vector
- 는 page i 의 importance 를 나타낸다
이에 대한 Flow Equation 은 다음과 같고, 이는 recursive equation 이다!
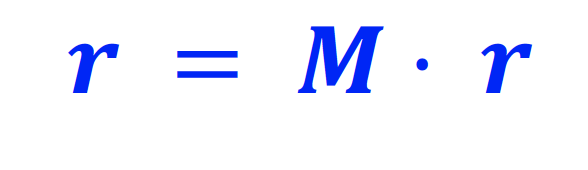
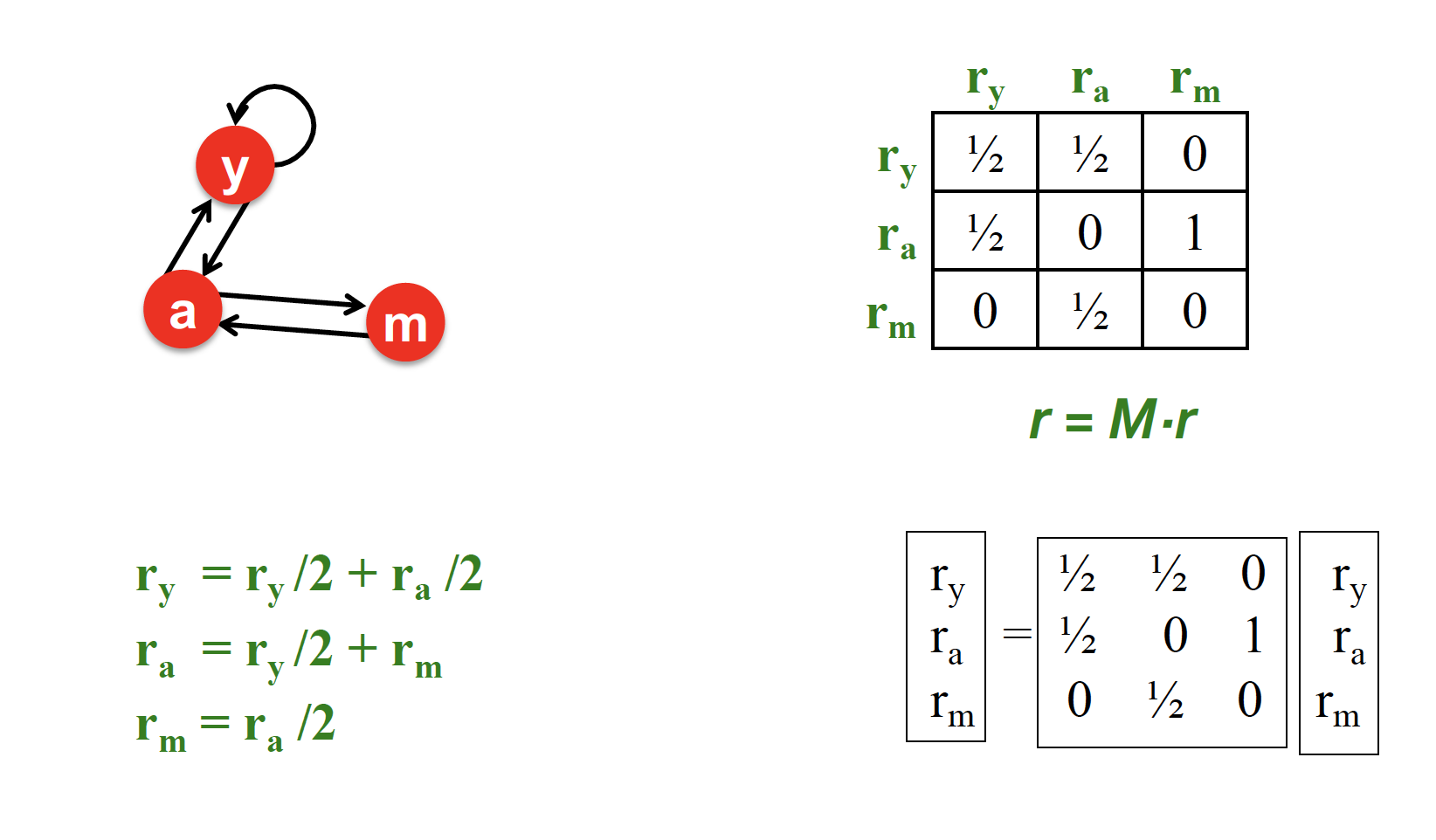
왼쪽의 3개의 방정식을 matrix formulation 으로 표현하면 오른쪽의 으로 표현되고, 계속적으로 rank vector 을 곱하면서 수렴할 때 까지 계산한다
Random Walk Interpretation
PageRank 는 stationary distribution 으로부터 착안된 idea 라고 한다
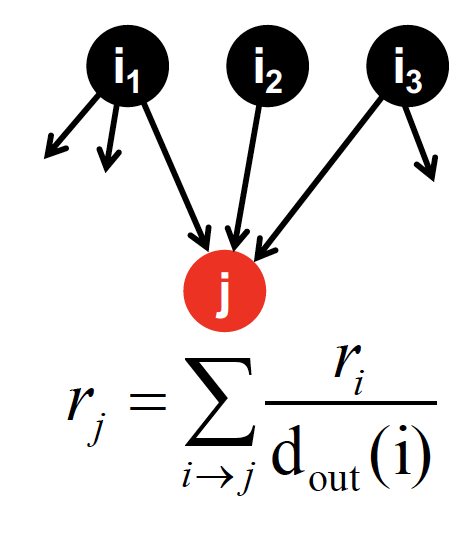
time t 에서, page i 를 탐색하고 있다고 할 때,
time t+1 에서는 uniformly random 하게 결정된 out-link 를 따라서 page j 로 이동하게 된다
page j 에서의 중요도 는 위의 값들 (in-link 로 부터 들어온 값들)을 다 더해서 계산된 것이고, 이 과정을 무한히 반복하게 된다
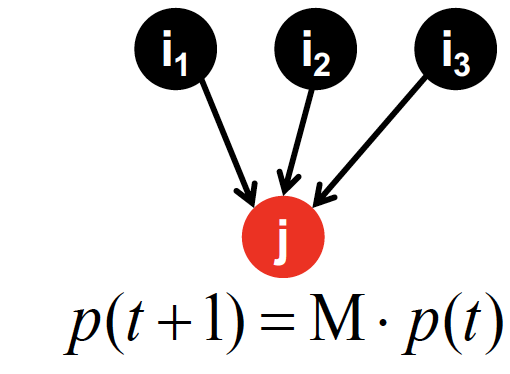
: probability distiribution over pages
time t+1 에 random surfer 가 어디에 있을까에 대한 확률 은,
로 계산이 된다
time t에 대한 확률에, stochastic matrix 를 곱해서, 다음 시점에 있을 확률을 계산한다
이 때, random walk 가 특정 state 로 수렴하게 된다 (Markov Chain) 고 가정하게 된다면,
라는 식을 만족하게 된다
따라서 이라는 flow equation 에서,
rank vector 은 random walk 에서의 Stationary Distribution 이다!
✔︎ Stationary Distribution
를 만족하는 를 stationary distribution 이라고 한다.
어떤 Transition 확률 () 이 존재할 때, Transition 발생 횟수에 상관 없이 vector 가 동일한 로 남는다는 의미이다.
즉, 특정 State 가 발생할 확률이 항상 같다!
Power Iteration
flow equation :
위의 식에서 rank vector 은, stochastic web matrix 의 eigenvector 임을 알 수 있다!
✔︎ eigenvalue decomposition : ,
flow equation 에서 eigenvalue 에 대응되는 eigenvector 는
임의의 node u 에서 출발해서 random walk 를 진행했을 때,
이 된다면, 이 됨을 알 수 있고,
이 의 principal eigenvector (가장 큰 고유값에 대응하는 고유벡터) 가 되는 것을 알 수 있다
따라서 을 통해 PageRank 를 계산한다 ~
PROCESS
Initialize:
각 node 는 균등한 가중치로 시작된다Iterate:
연결된 node 로 부터 가중치를 넘겨받는 과정이 재귀적으로 반복된다Stop: when
Repeat until convergence to the solution!
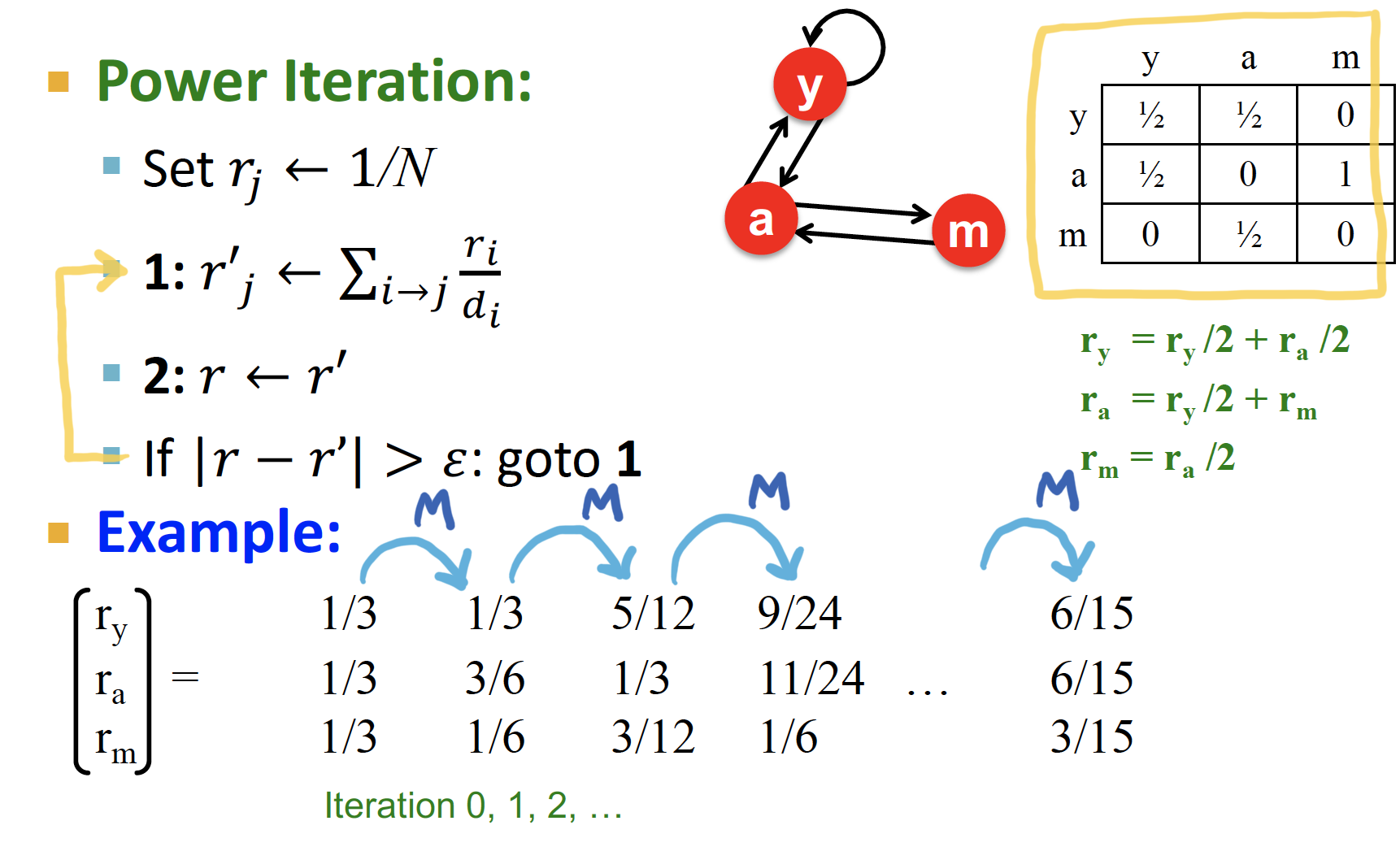
바로 위에 적었지만 다시 적어 보면.. ㅎㅎ
1. 각 node 는 균등한 가중치에서 시작된다
2. 연결된 node 로 부터 가중치를 넘겨받는 과정이 재귀적으로 반복된다
3. 오차가 특정 값으로 수렴할 때 까지, multiply 을 하면서 반복한다
Problems
그런데... PageRank 를 적용하면 다음과 같은 문제에 직면하게 된다
1. 실제 그래프에서 converge 하긴 하나 ~?
2. 수렴하면 우리가 원하는 대로 수렴 하려나 ~?
3. 결과가 reasonable 한가 ~?~?
1. Dead Ends : Does this Converge?
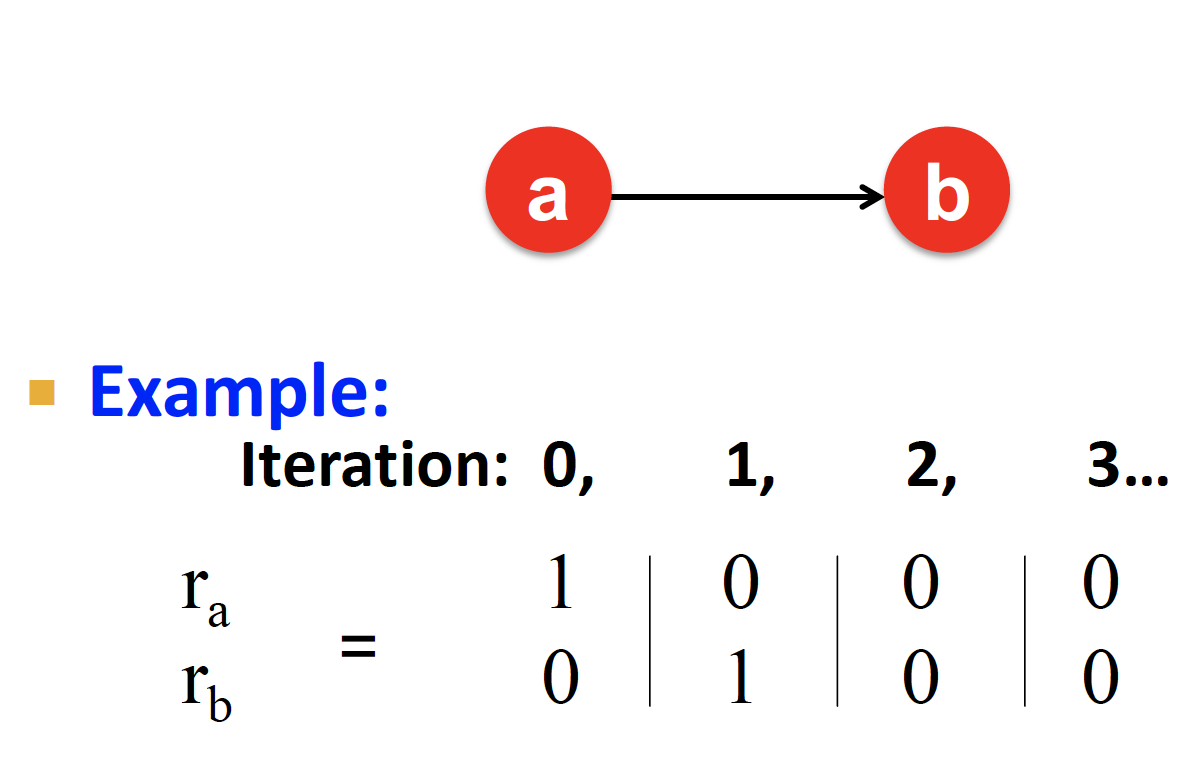
out-link 가 없어서, importance 의 leakage 를 유발하는 문제!
Adjacency Matrix () 가 더 이상 stochastic 하지 않을 수 있어서, 특정 칼럼의 합이 1이 아니라 0이 될 수도 있는 문제가 발생한다
이러한 행렬로 flow equation을 계산하면 의 일부 혹은 전체가 0이 되어 버릴 수 있게 된다...
따라서 PageRank 수렴에 문제가 생긴다
2. Spider Trap : Does it converge to what we want?
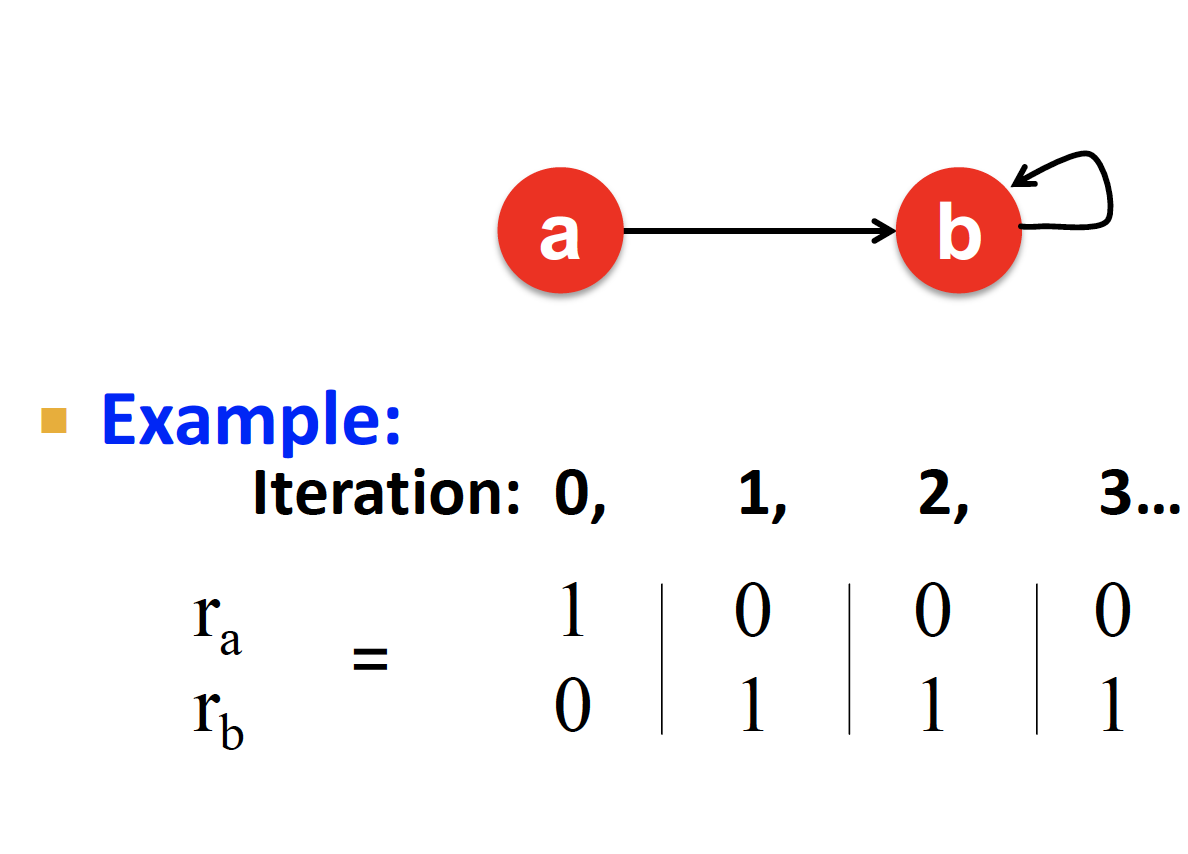
모든 out-link 가 group 에 속해 있을 때, 모든 importance 는 해당 group 이 다 흡수해 버리는 문제!
PageRank score 에 문제가 생긴다
(여기서 교수님이 1번이랑 2번 문제 바꿔서 말씀하신 것 같음...🤨)
Solutions : Teleports
1. Teleports for Dead Ends
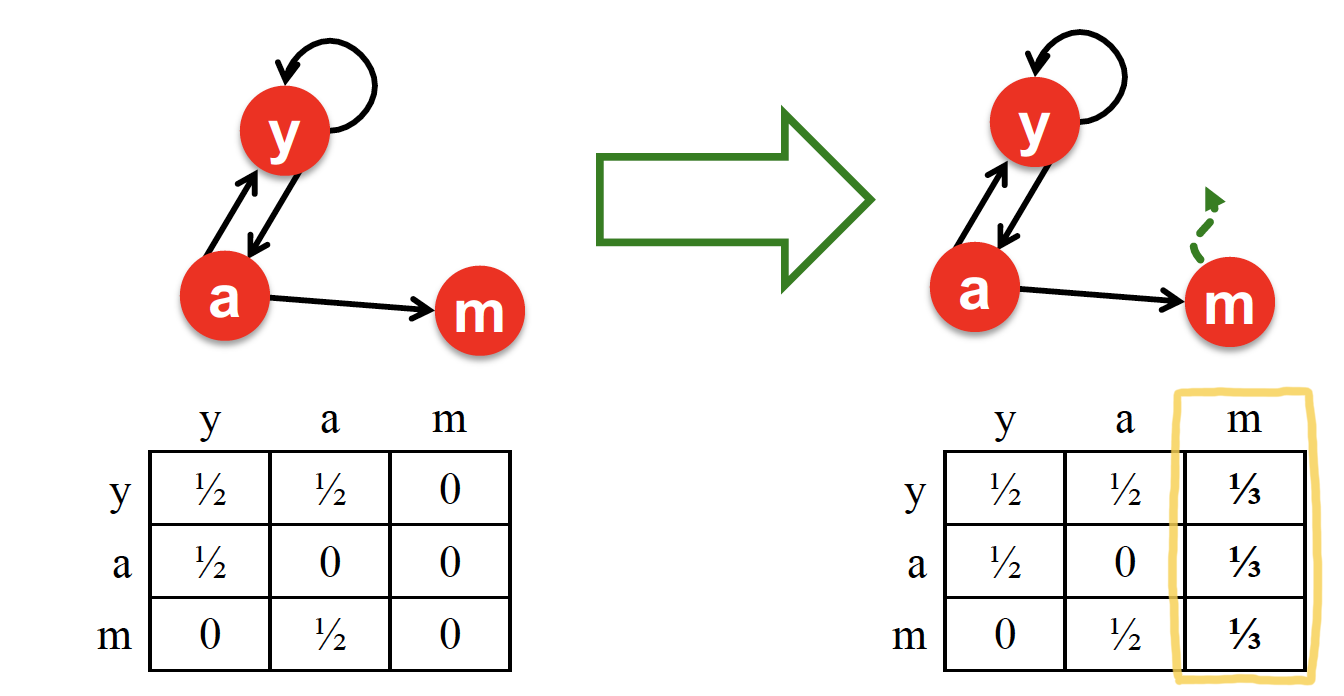
막다른 길에 다다른 node 에게, 균등한 확률을 배분한다
Dead end node m 이 다른 node 로 갈 확률의 전체 합은 1 이다
2. Google Solution for Spider Traps
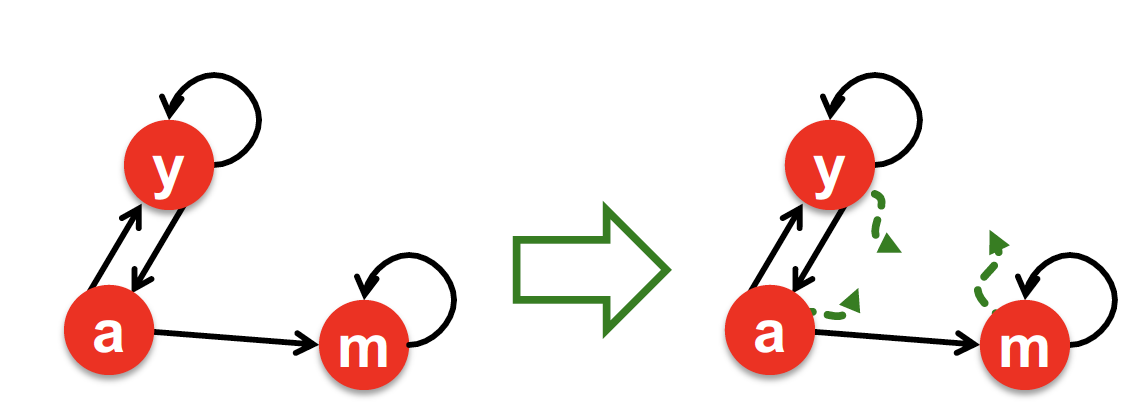
각 time step 마다, random surfer 는 2가지 option 이 생긴다
1. : link 를 그대로 따라갈 확률
2. : random page 로 jump 할 확률
일반적으로 는 0.8 ~ 0.9 사이의 값으로 설정한다
(-greedy 알고리즘 느낌 ...)
Google Matrix : Random Teleports
따라서 위의 두 가지 문제점인 Dead Ends 와 Spider Traps 를 해결하기 위해, 아래와 같은 식을 세워 PageRank equation 을 계산한다
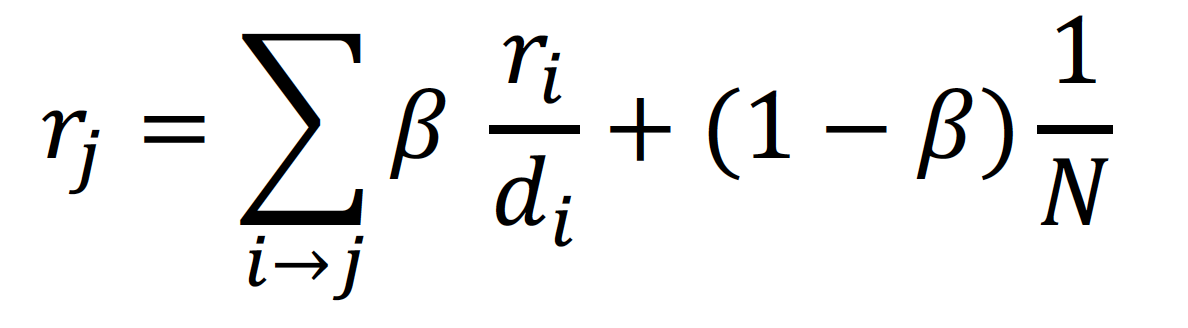
이를 Google Matrix 행렬식으로 표현하면 다음과 같다!
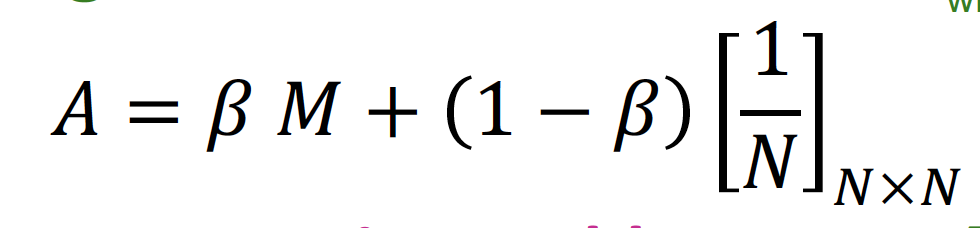
Example of Random Teleports
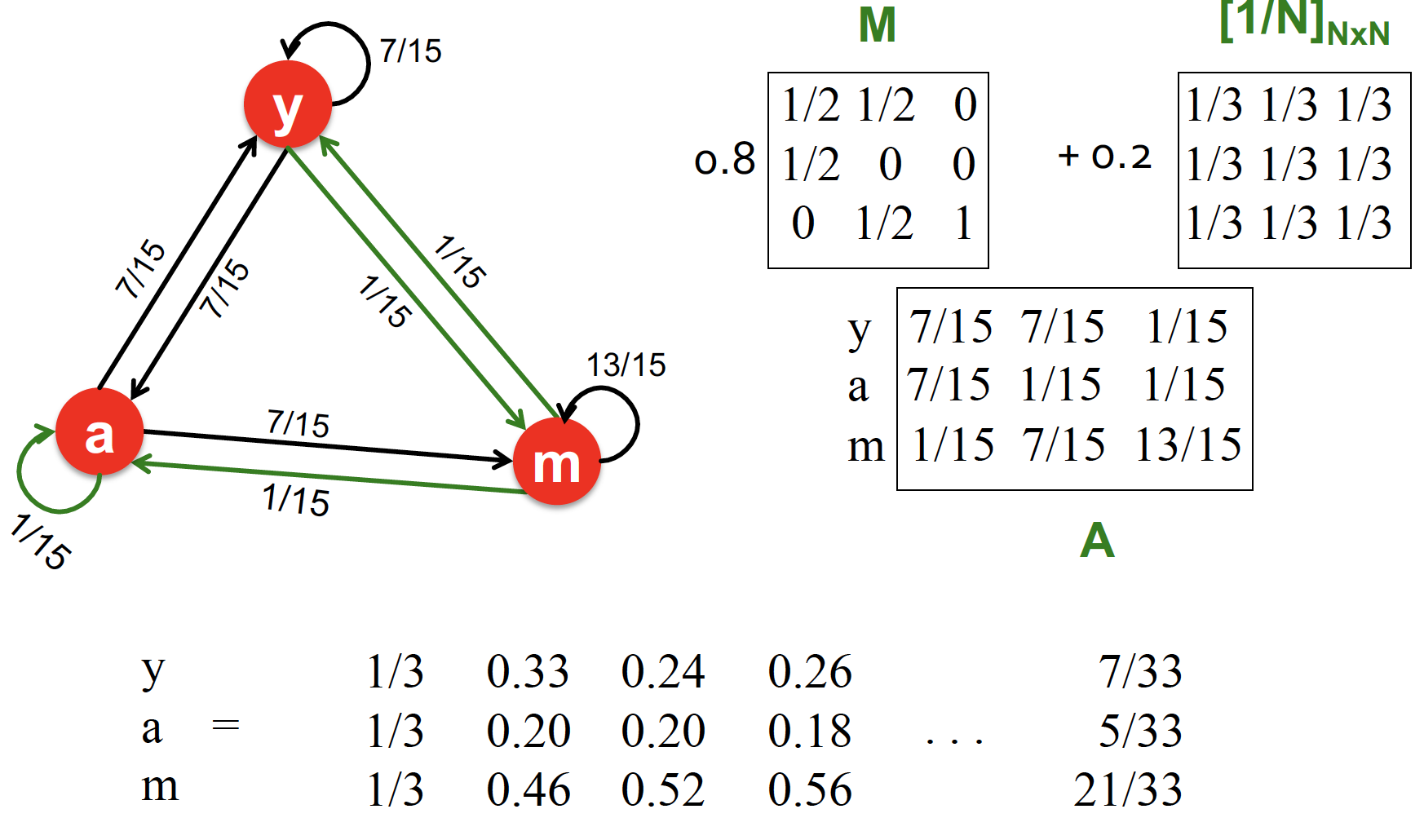
Computing PageRank
그런데.. 만약 N=10억 page 라고 ☀️ 보자..
Google Matrix :
는 개의 entry 를 갖고 있는 어마무시한 행렬이 될 것...
따라서, PageRank equation 을 Rearrange 한다 ~
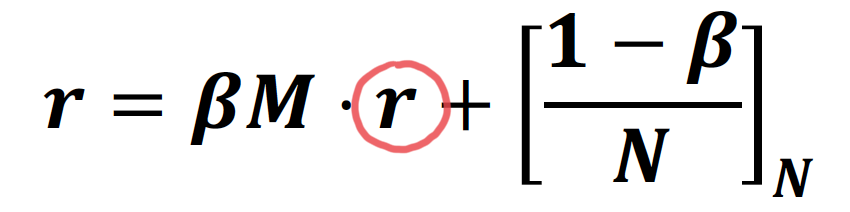
위의 식에서, 은 sparse matrix 이다!
Google Matrix 를 통해 PageRank 를 계산한다는 것은, 을 계속 계산한다는 의미이다! 즉, sparse matrix 가 아니라, 1/N 값을 더해서 만든 dense matrix 를 계속 곱하고 곱해서 계산한다는 것이다... 당연히 연산량이 넘쳐날 수 밖에 없음
따라서 Rearrange 한 식으로 PageRank 를 계산한다는 의미는,
1 step 마다 Sparse matrix 를 곱하고, 그 때마다 1/N 을 따로 더한다는 의미이다
sparse matrix 를 곱해 가는 것이기 때문에 연산량이 줄어든다는 의미 ~

알고리즘으로 적어 보면 위 처럼 표현된다 ~
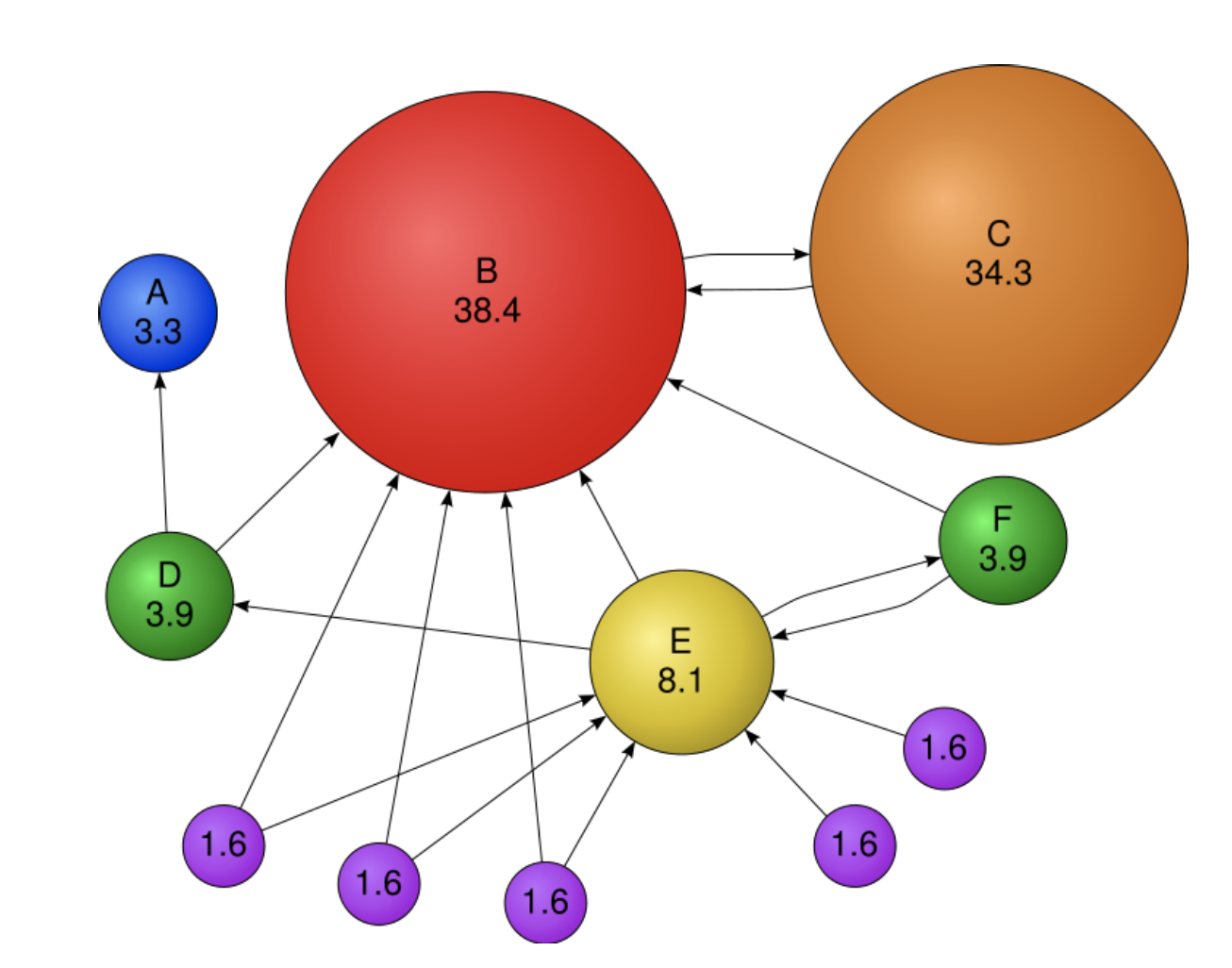
Example
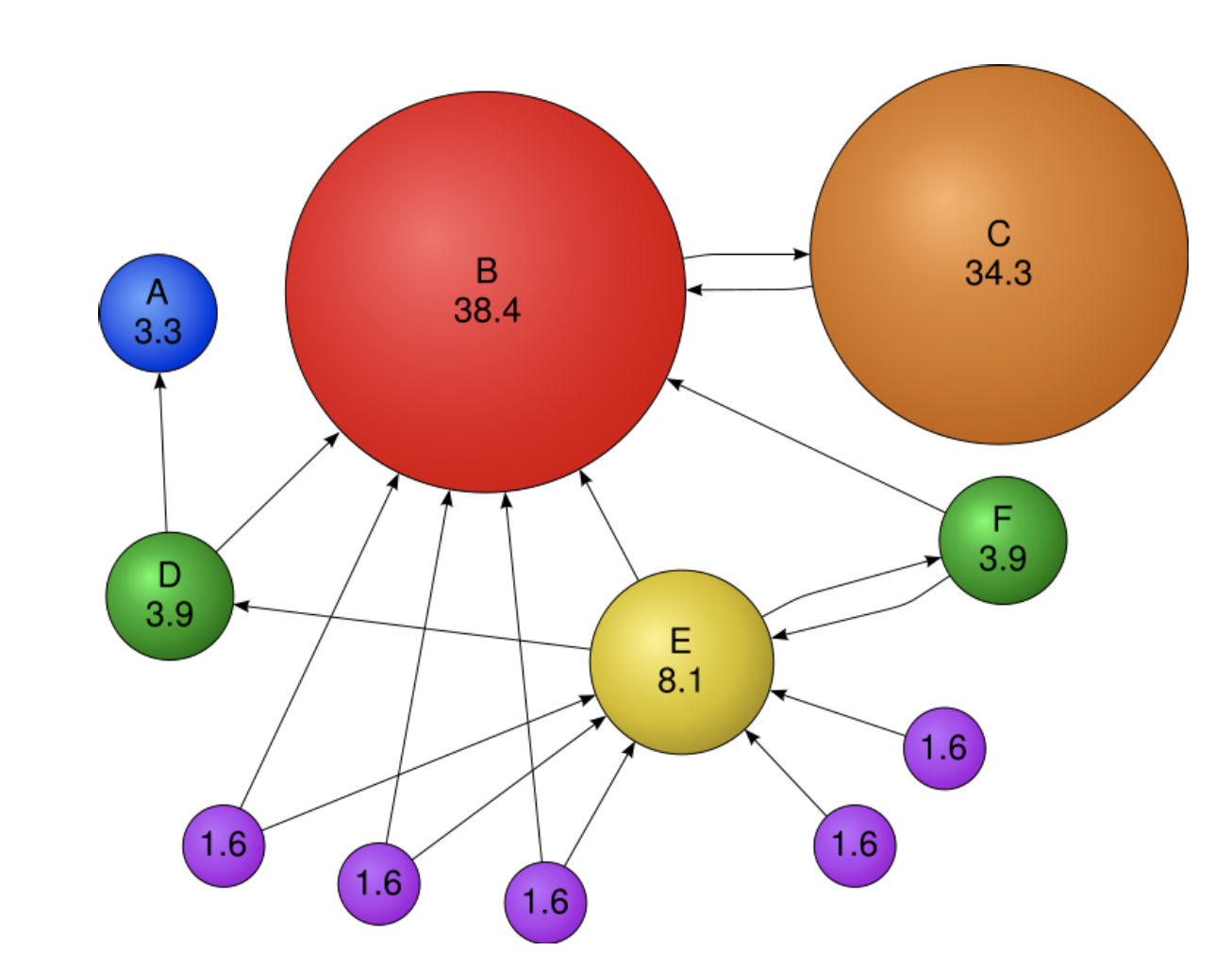
PageRank 를 통해 계산한 결과를 그림으로 표현하면 위와 같다
page C 의 경우, in-link 가 하나이지만, 중요한 page 인 B 로부터 out-link 를 받았기 때문에 굉장히 score 가 높은 것을 볼 수 있다!
Reference
- 그천 윤종이의 띵강 & velog 리뷰
- Tobigs Graph Study : Chapter11. Link Analysis: PageRank
- snap-stanford Review : PageRank
- Seungkwan's Lab. : 강결합 컴포넌트 (Strongly Connected Component)
- Kim Hyungjun님 medium : Markov Chain & Stationary Distribution
- TextRank 설명이 아주 잘 되어 있는 글 : TextRank 기법을 이용한 핵심 어구 추출 및 텍스트 요약
