15. Outbreak Detection in Networks

tobigsGNN·2021년 4월 5일

CS224W GNN Outbreak Detection

CS224W Review

목록 보기

15/18

작성자 : 정민준

이번 강의에서는 네트워크에서 특정 사건이 발생하고 이를 어떤방식으로 탐지하고 처리하는 방법에 대해서 소개합니다.

먼저 문제에 대해서 정의하고 이를 해결하는 알고리즘 중 그리디하게 접근하는 hill-climbing 알고리즘에 대해서 소개합니다.

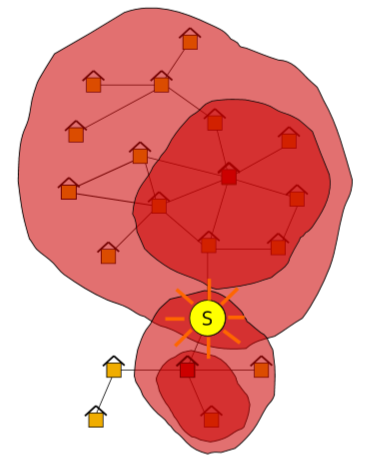
사진의 네트워크의 노드는 가정집이고 간선은 수도로 정의합니다.
여기서 수질오염이 발생하여 이를 센서를 통해 탐지하고자 합니다. 센서를 모든 노드마다 배치하여 수질오염을 탐지할 수 있으면 좋겠지만 아시다시피 정해진 cost내에서 센서를 효율적으로 배치하여 수질오염을 탐지하는게 목표입니다.

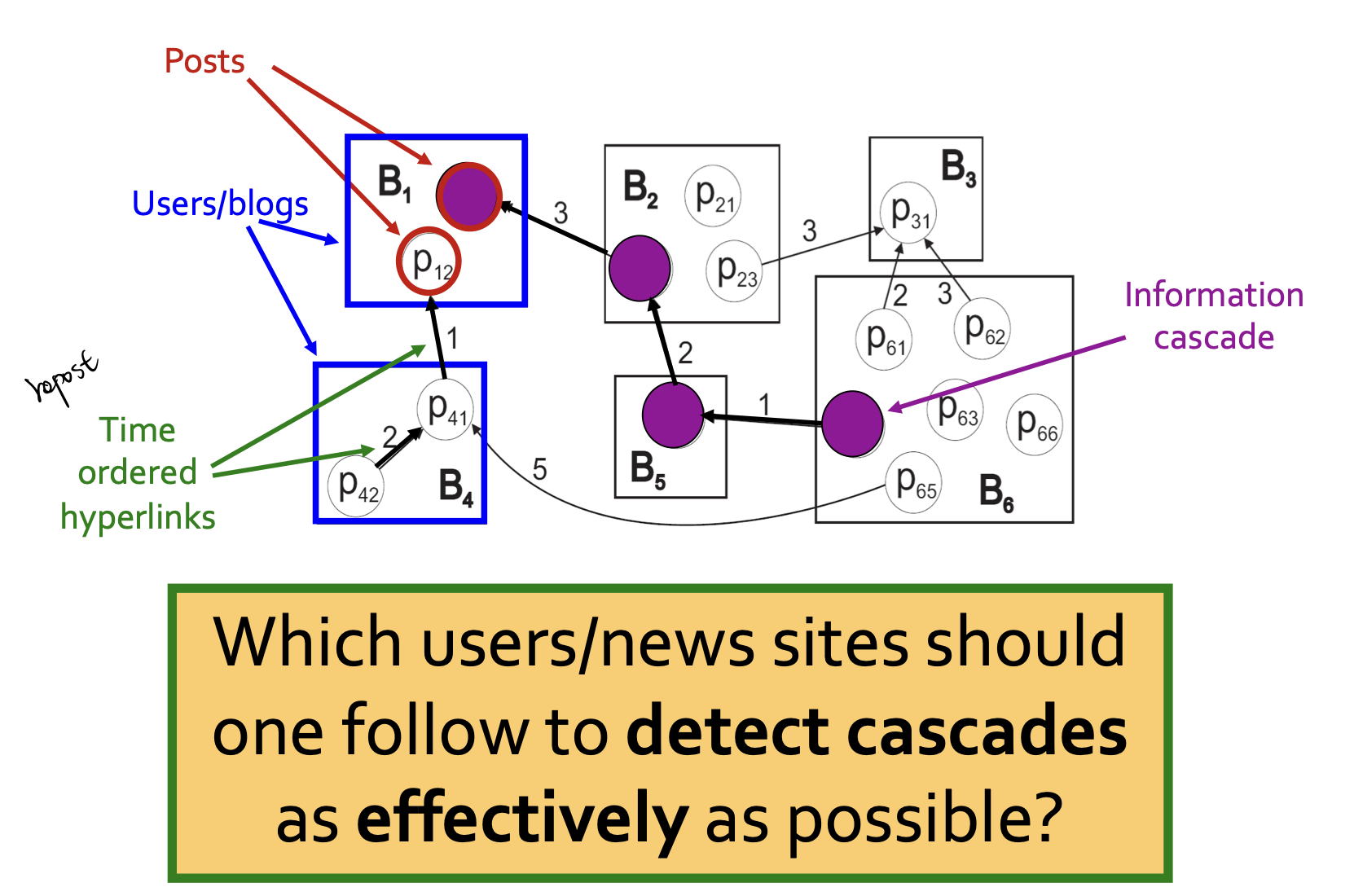
여기서 파란 박스를 유저로 두고 박스 내에 있는 p는 post, 글입니다. 어떤 포스트를 따라가야 repost된 관계 구조를 효율적으로 파악할 수 있을까가 문제입니다. 이는 위에서 소개했던 예시와 유사합니다.

주어진 네트워크 내 노드를 선택하여 문제를 효율적으로 탐지하고자 합니다. 이는 전염병, 네트워크 보안등에 적용될 수 있습니다.

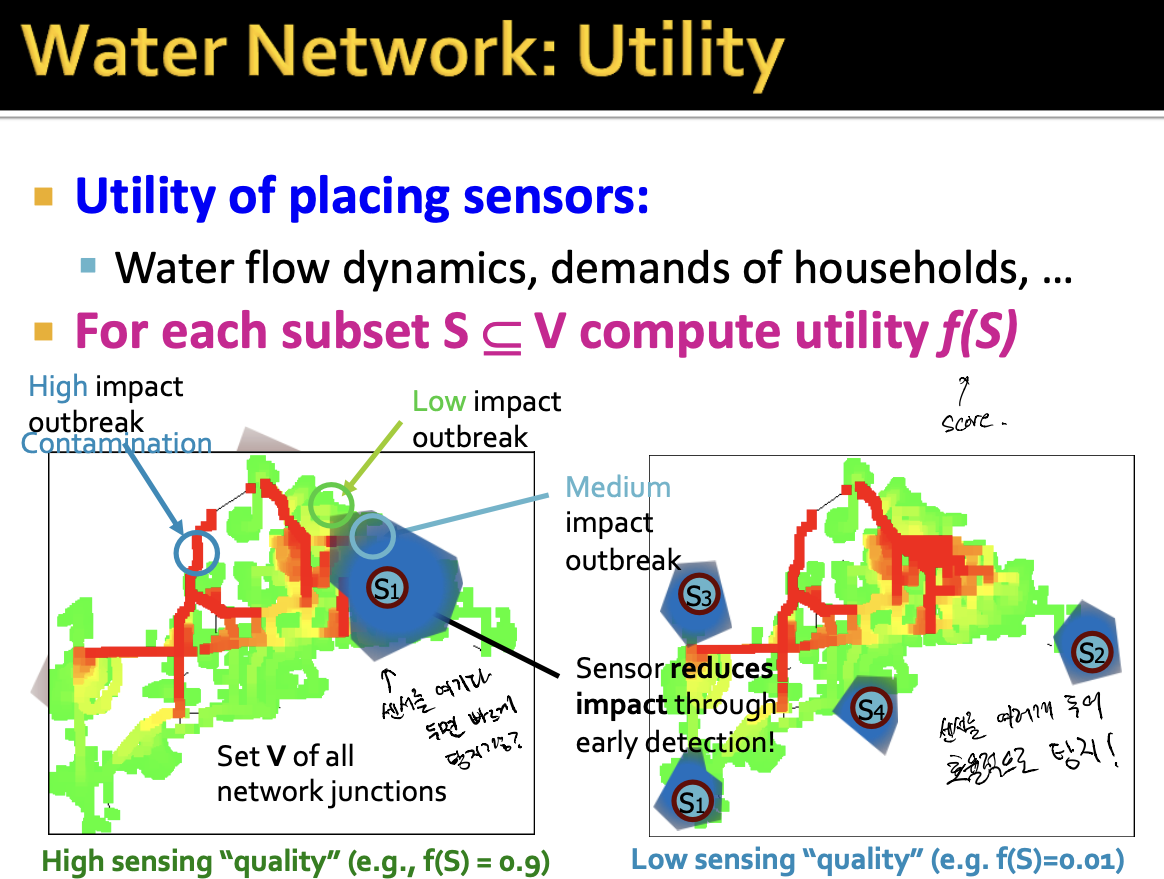
센서위치를 어디에 두는지에 따라 센서가 탐지하는 범위가 달라집니다. S1의 경우는 넓은 범위를 탐지하지만 오른쪽에 센서들은 작은 범위만을 탐지합니다.
여기서 trade off는 여러개 센서를 두어 효율적으로 일찍 탐지를 할것인지 아니면 늦게 탐지하더라도 넓은 범위를 탐지할 수 있도록 센서를 둘것인지를 결정해야합니다.

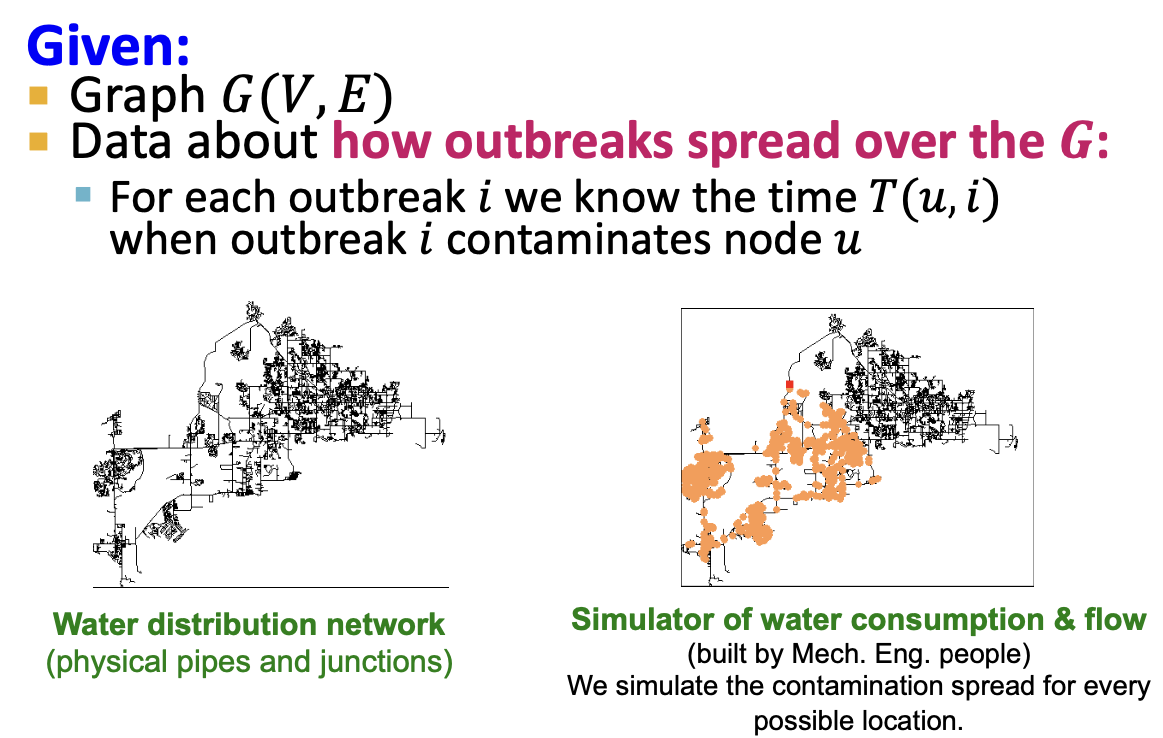
주어진 그래프에서 u 노드가 사건을 탐지하는데 걸리는 시간을 다음과 같이 정의합니다.

그래서 가장 큰 reward를 얻을 수 있는 노드 집합을 찾아 고르는 것이 우리의 목표입니다. 여기서 cost는 주어진 예산보다 작아야 합니다.

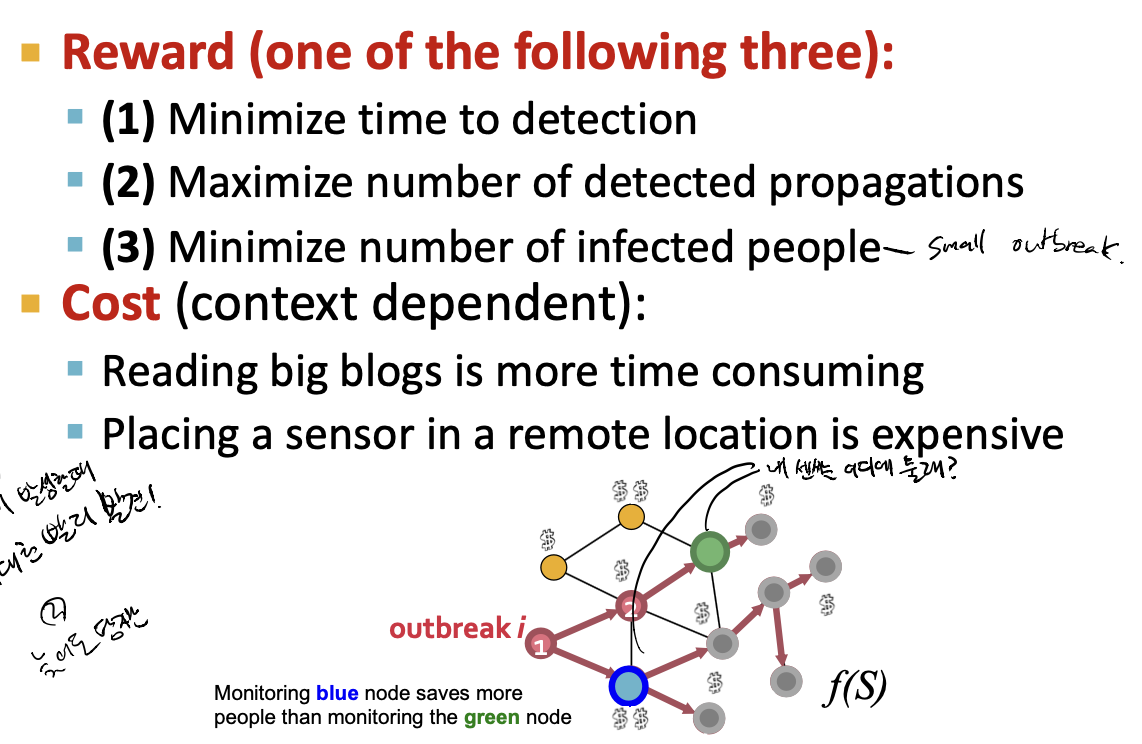
여기서 reward의 가치는 다음과 같이 둘 수 있습니다. 이전에 언급했듯이 사건 탐지를 가장 빠르게 할것인지, 느리게 탐지하더라도 넓은 범위를 커버하는지가 있습니다.
연결이 너무 많이된 노드에 센서를 두면 탐지하기 위해 많은 시간을 사용합니다.

Time to detection : 오염을 탐지하는데 걸린 시간.
Detection likelihood : 얼마나 오염을 탐지하였는지.
Population affected : 얼마나 많은 사람들이 오염된 물을 마셨는가.
여기서 중요한 점은 무조건 빨리 탐지하는게 좋다고 교수님께서 말씀 하셨습니다. 이 점을 이용하여 후에 그리디한 알고리즘으로 문제를 해결한다고 저는 이해했습니다.

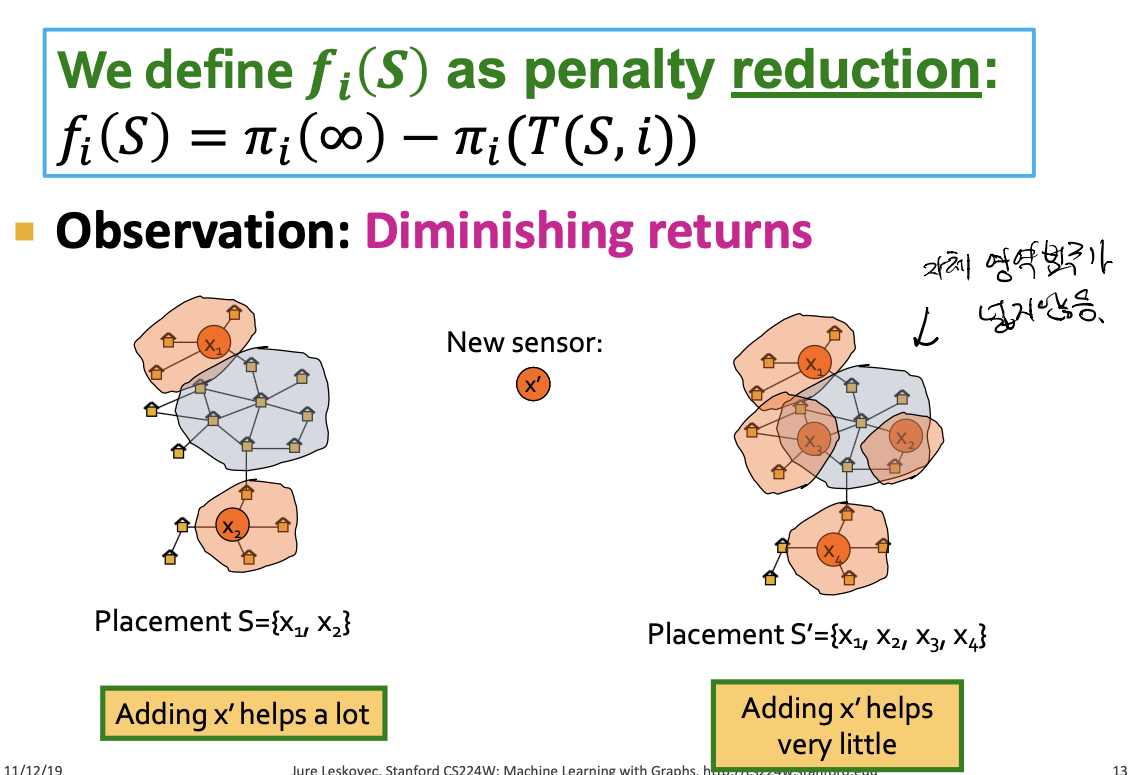
다음과 같이 목적함수를 정의합니다.
왼쪽에서 새로운 센서를 다음과 같이 두면 효율적으로 오염을 탐지할 수 있습니다. 하지만 오른쪽에 똑같이 적용하면 왼쪽에서만큼 효율을 발휘하지 못합니다.

A, B는 주어진 그래프의 노드 셋입니다. 서브 그래프 개념으로 본다면 B는 A를 포함하는 더 큰 서브그래프인 셈입니다.
위의 식이 성립하는 이유는 앞서 센서가 겹쳐서 탐지하는 부분이 많다면 효율이 떨어지는 경우를 보았습니다. 이처럼 A가 B의 부분집합일 때 A에 센서를 추가하는것이 B에 추가하는것 보다 더 효율적일 수 있습니다.
탐지하는 시간의 경우를 세 가지로 나누어 봅니다.
첫번째 경우는 x 센서를 두어도 탐지하는데 가장많은 시간이 걸리기 때문에 필요가 없습니다.
두번째 경우는 A에 대해선 더 좋지만 B에는 아니라는 점입니다.
세번째 경우는 x가 A,B보다 빨리 탐지합니다.
그래서 우리가 사용하는 목적함수는 Submodular라는 것입니다.

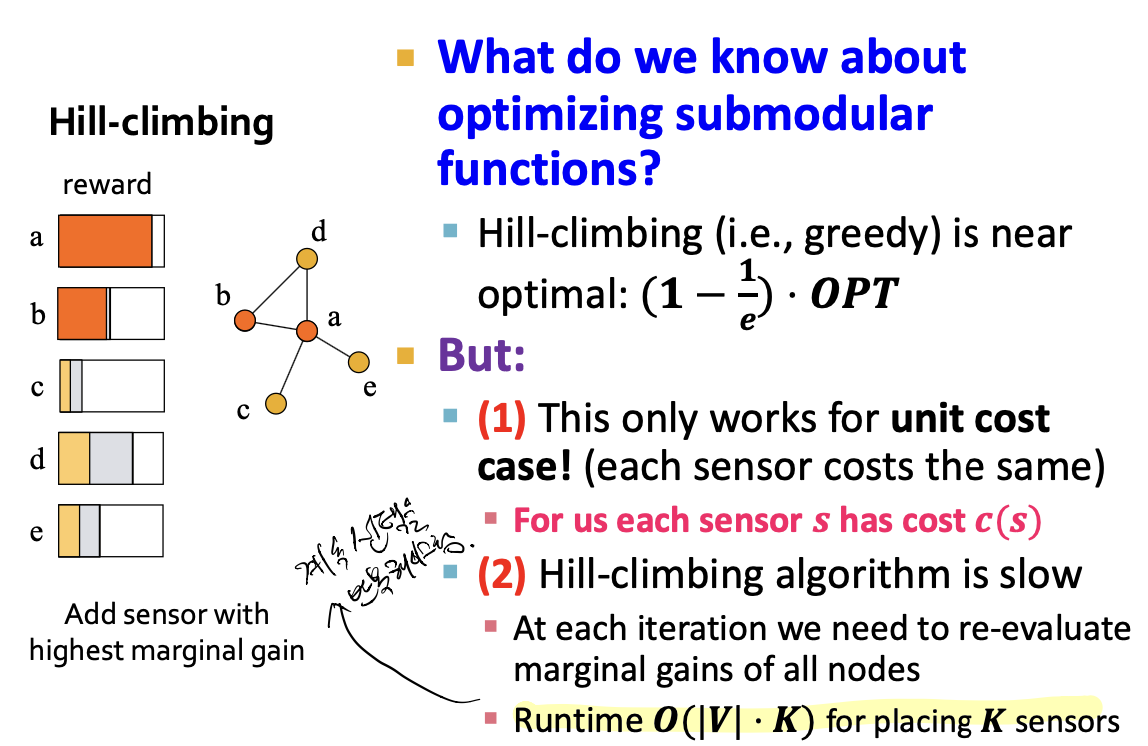
매번마다 노드의 reward를 갱신하고 이를 선택하는 알고리즘입니다. 하지만 특정 문제에서만 해결 가능하며 시간복잡도가 느린 알고리즘입니다.
Hill-climbing은 노드 자체의 cost를 무시합니다. 그리고 이 방법을 사용하면 가진 예산을 금방 낭비할 가능성이 큽니다. 고의적으로 최선을 선택하지 못하는 상황이 발생합니다.

여기서 n개 센서에 B 예산을 가지고 있습니다. s1은 r과 B를 가지는데 나머지 센서의 reward는 s1보다 작습니다. 따라서 Hill-climbing 알고리즘을 적용하면 s1을 선택하게 되고 주어진 예산을 전부 사용하게 됩니다. 하지만 나머지 센서들을 여러개 선택할 수 있고 더 좋은 reward를 얻을 수 있었지만 s1을 택하게 되는 현상이 발생합니다.
따라서 이를 조율할 수 있는(최적화 할 수 있는) benefit-cost ratio를 적용합니다. 하지만 이또한 위와 유사한 문제가 발생하게 됩니다.

CELF 알고리즘은 그리디 알고리즘을 적용하여 두 결과중 최적의 결과를 선택합니다. 앞서 발생한 문제가 있었지만 그래도 정답과 유사한 결과를 선택할 수 있다고 합니다.

여기서 각 노드들의 Marginal gain을 고려하여 탐색을 진행하는데 S1이 a인 상태에서 gain을 구했고 남은 노드들에 대해서도 구하고 정렬합니다.
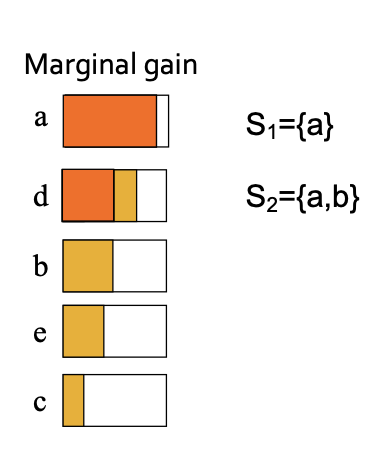
a를 서브셋에 넣고 다음 노드들을 집합에 넣어 marginal gain을 다시 계산합니다. 이를 반복적으로 적용하여 셋을 구합니다.
무조건 marginal gain이 높은걸 선택해야 최적화된 답입니다. 이유는 이를 택하지 않는 최적의 경우의수가 있다고 생각했을 때 다른 노드를 선택하면 당연히 gain이 낮은것들만 선택함으로 greedy하게 접근하는 것이 가능합니다.

여기서는 Solution quality에 대해서 얘기합니다. 알고리즘을 통해서 구한 답은 정답이 아니라 정답에 가까운 답을 구해줍니다. Submodular 함수는 1-1/e의 바운드가 존재합니다.

여기서 델타 u는 u를 선택하였을 때 얻는 margin. 그리고 OPT는 구한 최적의 노드 셋을 의미합니다.
다음 식을 따라서 최적의 셋의 스코어가 다음 보다 작다고 정의하고 있습니다.

tobigsGNN

2021 투빅스 GNN 스터디

이전 포스트

14. Influence Maximization in Networks

다음 포스트

16. Network Evolution

1개의 댓글

2021년 4월 10일

Network 내에서 사건이 발생했을 때, 이를 효과적으로 탐지하는 방법에 대해 공부합니다.

node 를 선택하여 Network 내에서 발생한 문제를 효율적으로 탐지하고자 합니다.
이 때, 좁은 범위를 탐지하는 여러 개의 node 를 선택할 것인지, 넓은 범위를 커버할 수 있는 한 개의 node 를 선택할 것인지 등의 trade-off 를 결정하는 문제에 직면하게 됩니다.

여러 가지 경우를 고려하여 가장 큰 Reward 를 얻을 수 있는 subset S 를 선택하는 것을 목표로 하며, 이 때 발생하는 cost(S) 는 주어진 budget 보다 작게 되도록 합니다.
Reward 는 1. detection 시간이 짧아질수록, 2. propagation node 수가 많아질수록, 3. small outbreak 일 수록 높게 설정되며, neighborhood 가 많은 node 일 수록 탐지 시간이 길어지므로 cost 가 커집니다.

Objectives for Outbreak Detection

Penalty $\pi_i(t)$ : detecting outbreak i at time t
시간이 흐를수록 Penalty 는 무조건 증가하므로, 빠르게 탐지하는 것을 목적으로 설정합니다. 따라서 Greedy Algorithm 을 사용을 고려합니다.

Penalty Reduction
$f_i(S) = \pi_i(\infty) - \pi_i(T(S,i))$ 로 목적함수를 설정합니다.

여기서 $f_i(S)$ 는 submodular 입니다.
subset $A \subseteq B$ 에서, 포함관계에 있는 집합이 커질수록 늘어나는 증분이 감소하는 것을 말합니다.
해당 강의 예시에서, sensor 가 겹쳐서 탐지하는 부분이 있을 때 ( $A$ ), 여집합 ( $A-B$ ) 에 추가하는 것 보다 교집합 ( $A$ ) 에 추가하는 것이 더 효율적인 것을 볼 수 있습니다.

CELF Algorithm

지난 시간에 공부했던 Hill-climbing Algorithm 은, 매번 node 의 reward 를 갱신하고 이 때마다 선택하는 알고리즘입니다. 선택을 반복해야 하기 때문에 시간복잡도가 느리며, cost 를 무시할 수 있다는 단점이 있습니다.

cost 를 무시하게 되면, reward 만 보고 선택하게 되므로 비효율적인 선택을 할 가능성이 높아집니다.
이와 같은 문제를 해결할 수 있는 benefit-cost ratio 로 최적화를 진행해 보는 것을 고려해 보게 되지만, 이 또한 cost 와 benefit 의 값에 따라 최적의 선택이 불가능하게 될 수도 있다는 단점이 있습니다.

따라서 CELF Algorithm 을 통해 최적 subset 을 찾습니다.

CELF = Cost-Effective Lazy Forward-selection 이며,
1. Solution $S'$ : benefit-cost greedy
2. Solution $S''$ : unit-cost greedy

위 두 가지 방법론을 모두 고려하여
Final Solution $S = argmax(f(S'), f(S''))$ 를 선택합니다.

Submodularity Property 에 의해, $j>i$ 라면 $\delta_j \leq \delta_i$ (늘어나는 증분이 점점 감소) 하게 됩니다.
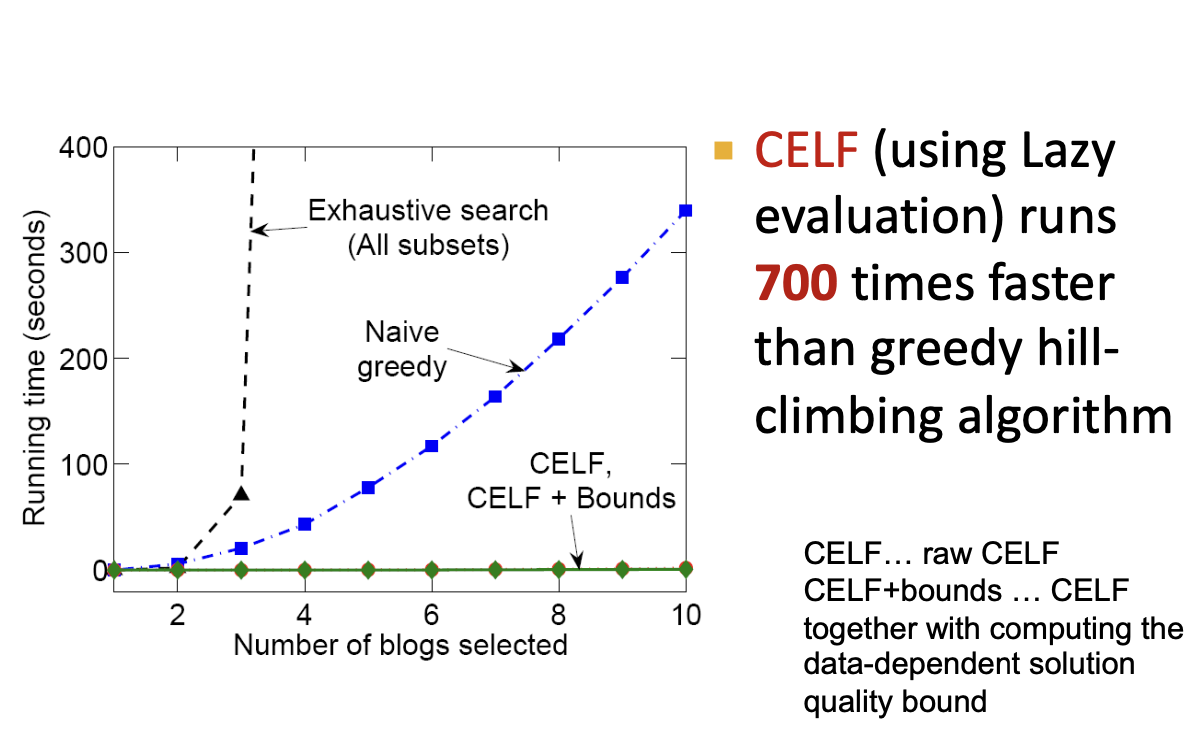
따라서 marginal gain 으로 재정렬 한 후, $\delta_i$ 의 top node 만 반복적으로 계산하는 Lazy hill-climbing 알고리즘을 통해 최적 해를 찾습니다.

띵강 감사감사 함니다 ~

답글 달기