16. Network Evolution

작성자 : 오진석

Contents

1. Introduction of Network Evolution
2. Macroscopic Evolution of Networks
3. Temporal Networks
4. Microscopic Evolution of Networks
5. Mesoscopic Evolution of Networks

---

1. Introduction of Network Evolution

Today, we'll be talking about evolution of networks and dynamic networks and how do we model that.

networks that change their structure over time.

이번 16번 강의에서는 시간의 흐름에 따라 구조가 바뀌는 network의 진화(변화), 동적 네트워크 그리고 그러한 네트워크를 모델링하는 방법에 대해서 다룹니다.

네트워크가 진화하는 과정을 네트워크의 규모적인 관점에서 다르게 바라보게 되며, 해당 관점에서 자세하게 다룰 수 있는 것들에 초점을 마추게 됩니다. 또한 진화 혹은 변화는 항상 시간적인 요소와 관련이 있기 때문에 이번 강의에서는 temporal한 특징을 자주 고려하여 네트워크를 다루게 됩니다.

사실 거의 모든 real world(복잡계)의 네트워크는 시간이 지남에따라 link와 edge를 추가하고 제거함으로써 evolve(진화)합니다. 아주 간단한 예시로, 우리는 새로운 친구를 사귈 수도 있고 친구를 잃을 수도 있기 때문에 친구 관계라는 네트워크에서 사람들(노드)이 추가되기도 제거되기도 합니다.

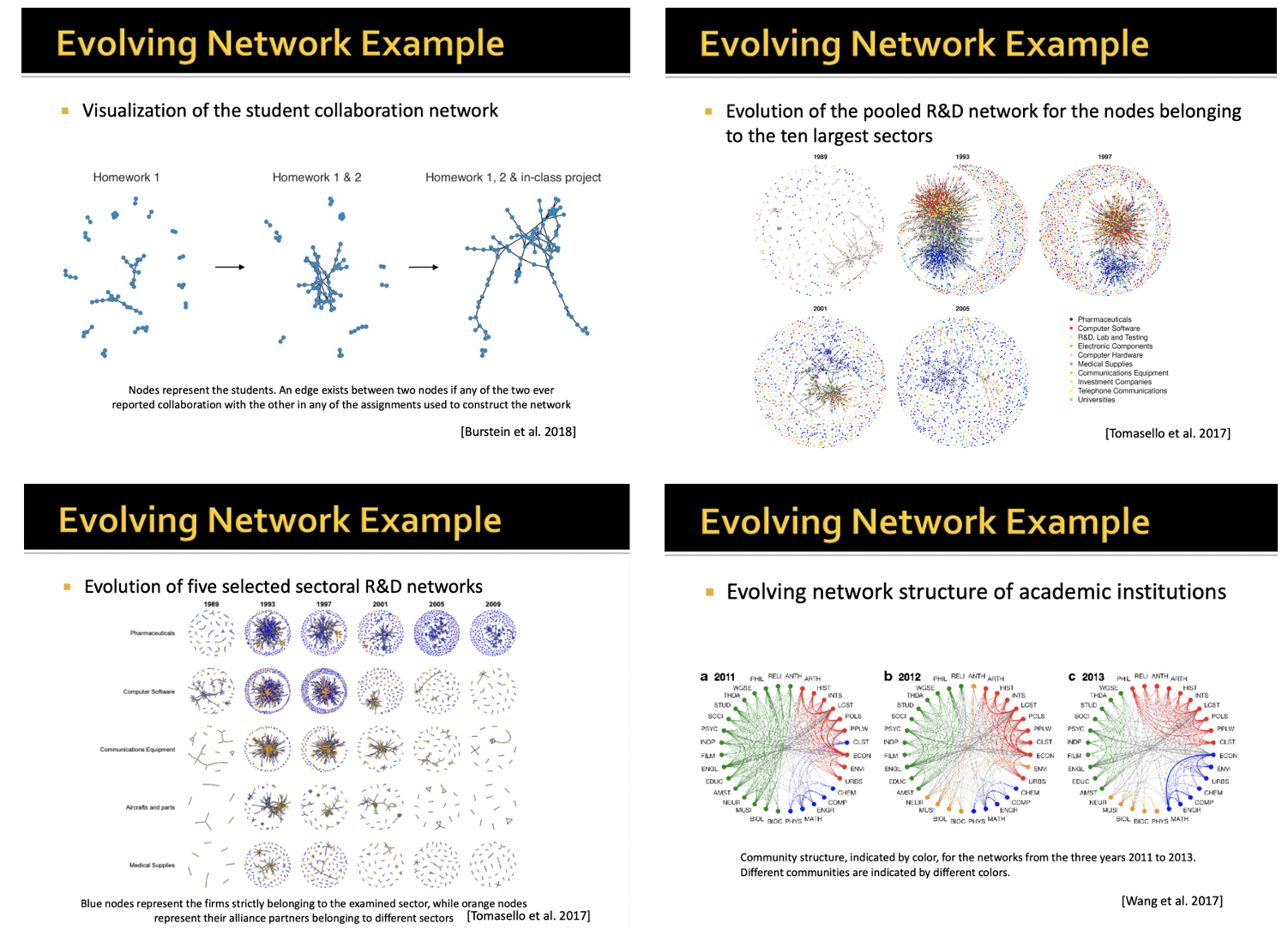
그 다음으로는 네트워크가 진화하는 예시를 보여주고 있습니다. 좌상단 첫번째 강의노트에서는 과제를 하면서 학우들과의 관계 네트워크가 진화하고 있음을 보여주고 우상단 두번째 강의노트에서는 10개의 큰 산업별 네트워크의 진화 과정이라고 할 수 있습니다. 하단의 예시들도 마찬가지로 시간의 지남에 따라 변화하는 네트워크를 보여주고 있습니다.

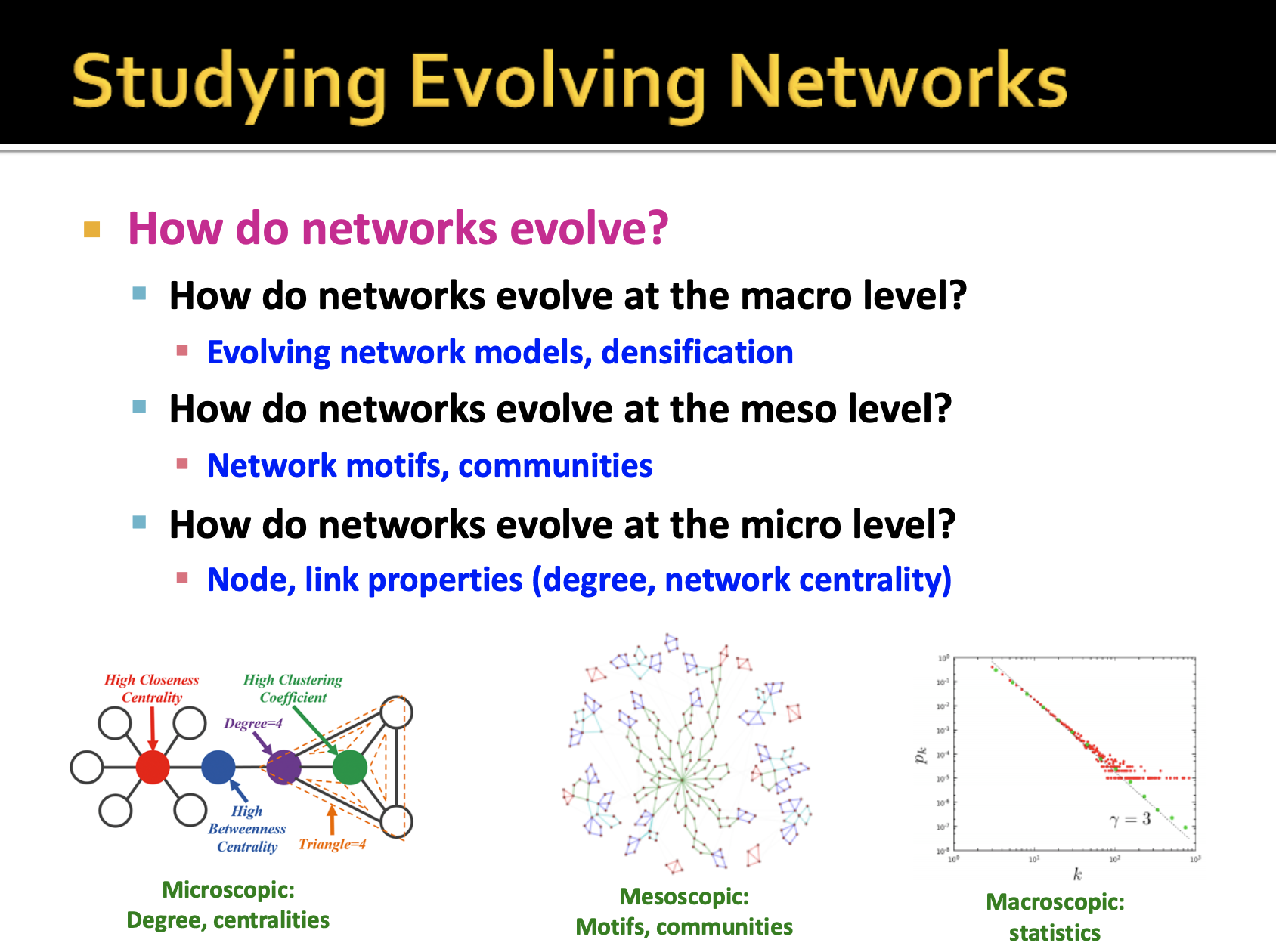
정리하자면, 오늘 강의에서 중점적으로 다룰 내용은 여러 다른 level에서 진화하는 네트워크를 연구하는 방법입니다. 여러 다른 level이란 네트워크의 규모적인 관점에서의 진화를 바라보는 것으로 이해했습니다.

• macroscopic level(거시적인 규모): 네트워크의 전체적인 구조의 특징이 시간에 따라 어떻게 변화하는지
• meso level(inntermediate scale): 네트워크 motif와 같은 보다 작은 substructures가 생겨나고 나타는지
• micro level: 네트워크가 변함에 따라 노드의 중요성 또한 어떻게 변화하는지

강의는 macroscopic level을 시작으로 micro level, 마지막으로 meso level 순서로 다룰 예정입니다.

2. Macroscopic Evolution of Networks

macro level에서 네트워크는 어떻게 진화할까요? 그리고 네트워크의 성장/확장의 전반적인 현상은 무엇일까요? 강의에서는 해당 질문의 포인트에 있어 3가지 question을 던집니다.

• 시간이 지남에 따라 노드의 수와 엣지의 수 간의 관계는 어떻게 정의할 수 있는가?
• 네트워크 성장에 따라 네트워크의 diameter(지름)은 어떻게 변화하는가?
• 또한 네트워크의 차수의 분포는 어떻게 변화하는가?

이 3가지 포인트 질문은 네트워크의 진화의 보편적인 원칙(universal law)을 통해 확인할 수 있습니다.

t 시점의 시간에서 N개의 노드와 E개의 엣지가 있습니다. 이 때, t+1 시점 혹은 미래의 시점에서 노드의 개수가 2N개가 되었다고 가정할 수 있습니다. 그렇다면 이 때, 엣지의 개수는 어떻게 될지 생각해볼 수 있습니다.

다양한 관점에서 생각해볼 수 있지만, 강의자는 다음과 같이 말합니다.

I actually argue that it's not clear why the number of connections should grow faster that the number of people(node).

이는 노드의 증가는 명백하게 몇 개가 증가했는지 알 수 있지만 노드와 노드와의 관계는 어떻게 설정되는지에 따라 증가할수도 감소할수도 있기 때문에, 노드의 증가에 따라 엣지가 증가한다는 사실을 명백하게 밝힐 수는 없다고 이해했습니다. 여기서 노드의 증가에 따라 엣지가 증가한다는 것은 어떻게 보면 보통은 당연할 수밖에 없는 상황으로 이해할 수 있습니다.

어쨋든 노드의 개수가 2개가 되는 시점에서의 엣지의 개수에 대한 답변은 2배 이상이라고 합니다. 이에 대한 답변?이유?는 Densification Power Law라는 것을 따른다고 합니다.

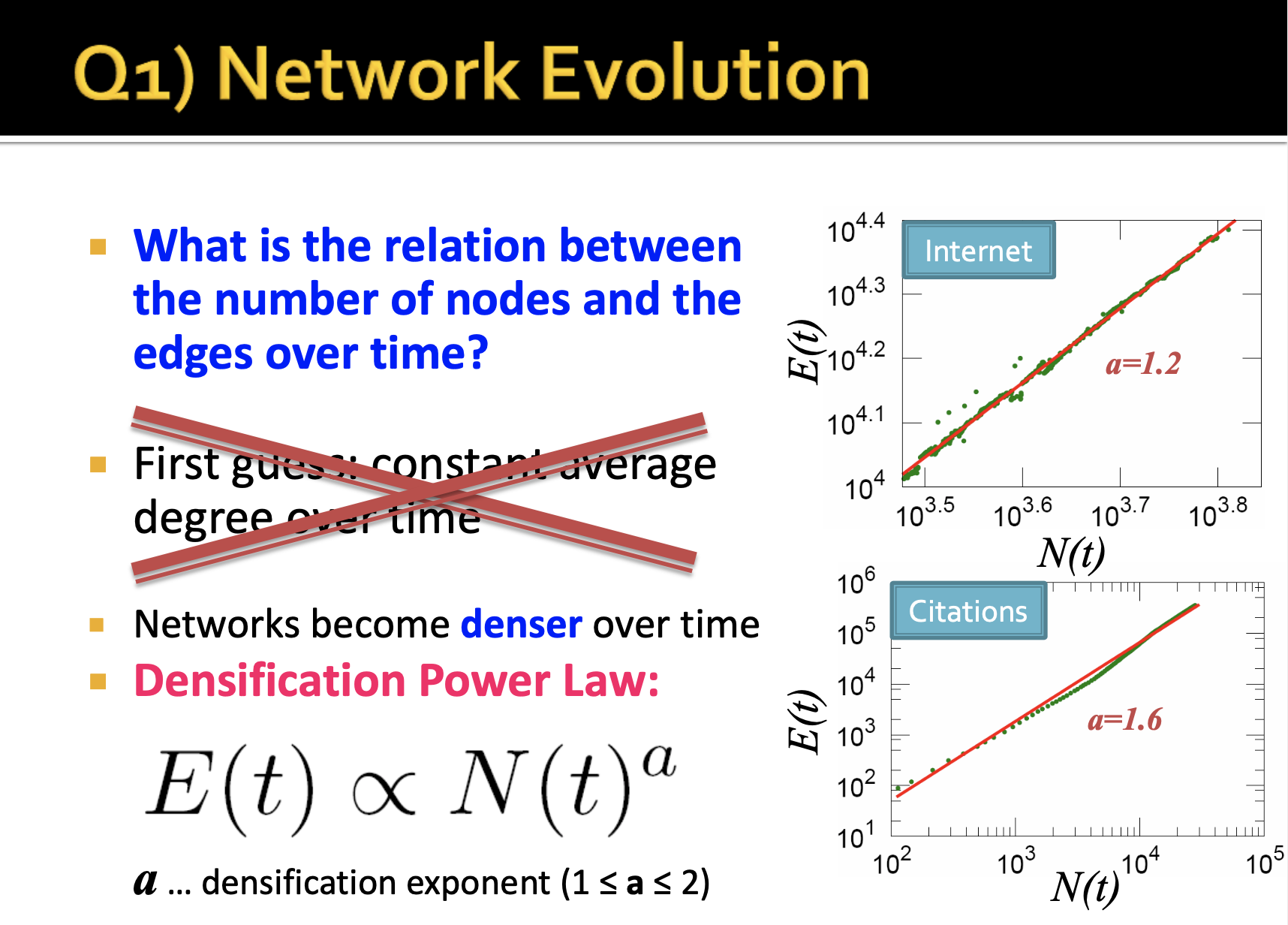
첫번째 포인트 질문입니다.

시간이 지남에 따라 노드의 수와 엣지의 수 간의 관계는 무엇인가?

우측의 Internet 네트워크와 Citations(참고문헌 관계) 네트워크의 로그 스케일상 노드와 엣지의 2차원 관계를 볼 수 있습니다. 각 포인트는 t시점마다의 노드의 개수와 엣지의 개수의 위치이며 결론적으로 노드와 엣지의 관계는 로그 스케일상 선형 관계를 가지고 있음을 알 수 있습니다.

이 때, 기울기는 0과 2사이의 값으로 표현될 수 있는데, 1.2와 1.6의 의미는 노드의 증가보다 엣지의 증가가 보다 빠르며 차수의 평균도 증가한다는 것으로 해석할 수 있습니다. 이러한 과정이 네트워크 진화에서 empirical observation이라고 할 수 있는 네트워크가 보다 빽빽(dense)해지는 Densification Power Law를 의미합니다.

정리하자면, Densification Power Law는 엣지의 수는 노드의 수보다 빠르게 증가하며 평균 차수 또한 증가함을 말합니다. 이 때 수식으로는 다음과 같이 표현할 수 있습니다. 이 때, 로그 엣지의 수를 로그 노드의 수로 나누게 되면 constant이다 라고 말하는데, 엣지의 수가 로그의 수보다 로그 스케일상 항상 일정 배수를 유지한다고 이해했습니다. (그런데 모든 시점에서 노드와 엣지가 going in/going out 하는 개수가 달라질텐데 로그 스케일상 constant한 배수를 가지는 것이 가능한지 잘은 모르겠습니다.)

앞서 언급했듯이, densification exponent는 엣지의 수가 노드의 수보다 빠르게 증가하기 때문에 1 이상의 값을 가지며 제곱의 형태도 증가하지 않기 때문에 2보다 작은 값을 가집니다. 값이 1이면 기울기값으로 증가하는 1차식 형태를 의미하게 되면 값이 2이면 2차식 형태로 증가하는 형태가 될 것 같습니다.

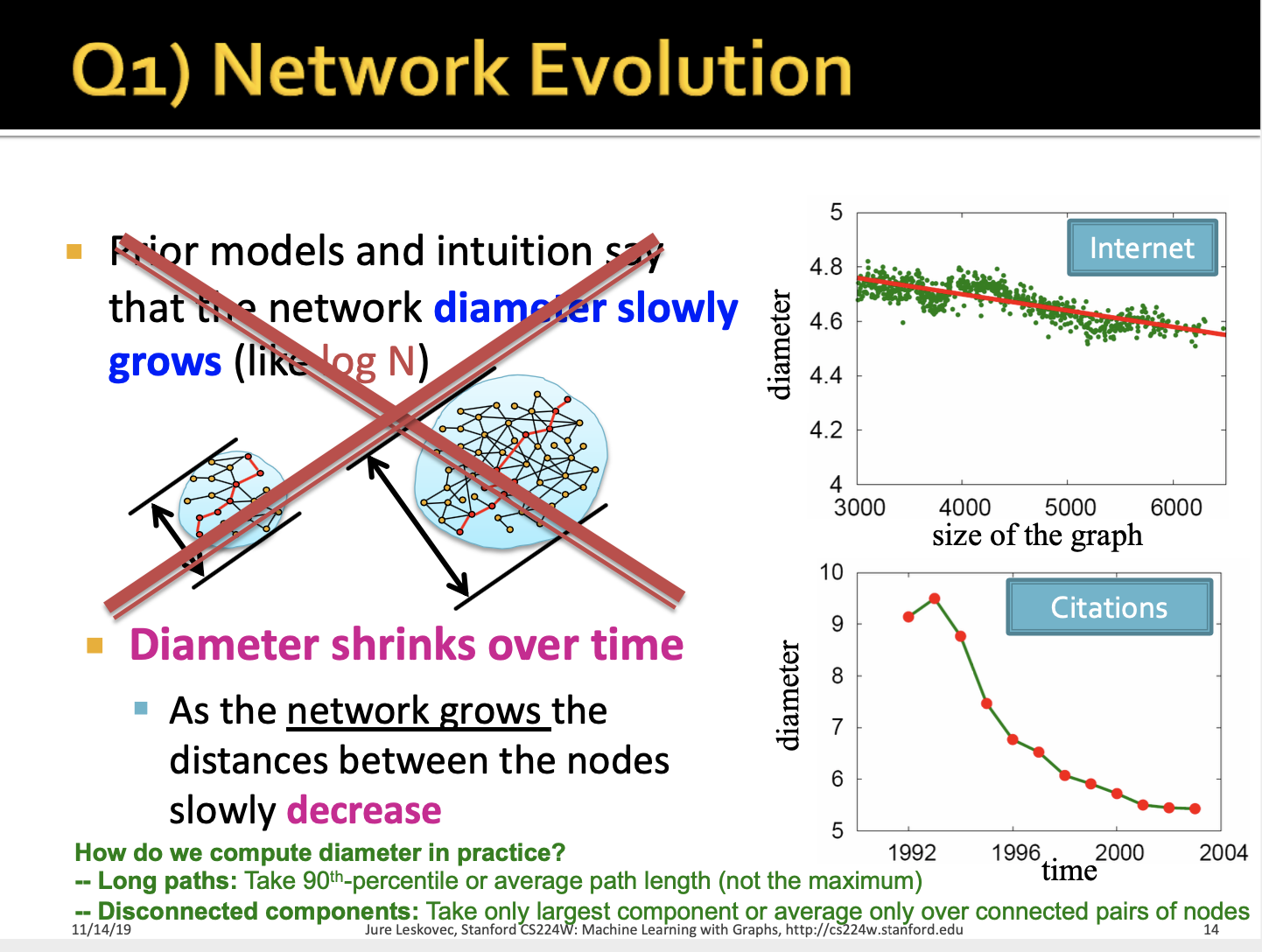
두번째 포인트 질문입니다.

네트워크 성장에 따라 네트워크의 diameter(지름)은 어떻게 변화하는가?

먼저 그래프 상에서 지름, Diameter는 정점 간 거리의 최댓값을 의미합니다.

강의 1과 2에서 다뤘던 랜덤 그래프의 직경은 노드의 수 N에 따라 logarithmically하게 증가한다고 했습니다. 예를 들어, 노드의 수가 적으면 logarithmically하게 직경은 보다 작을 것이고 노드의 수가 많으면 보다 큰 직경을 가지게 될 것입니다. 그러나 항상 옳은 사실은 아니라고 밝혀졌습니다. 이는 매우 반직관적인데(왜냐하면 시간이 지나면 노드가 증가할 것이고 그림처럼 직경 또한 증가할 것으로 예상하기 때문입니다.), 직접 직경을 측정해서 plot으로 그려보게 된다면 시간에 흐름에 따라 직경이 줄어듦을(shrinking) 알 수 있습니다. 우측 Internet 네트워크와 Citation 네트워크를 보게 되면 시간의 흐름에 따라 직경이 감소하고 있음을 확인할 수 있습니다.

네트워크의 크기가 증가함에도 불구하고 직경이 줄어든다는 의미는 노드 간의 거리가 천천히 감소가고 밀도가 증가했다고 해석할 수 있습니다.

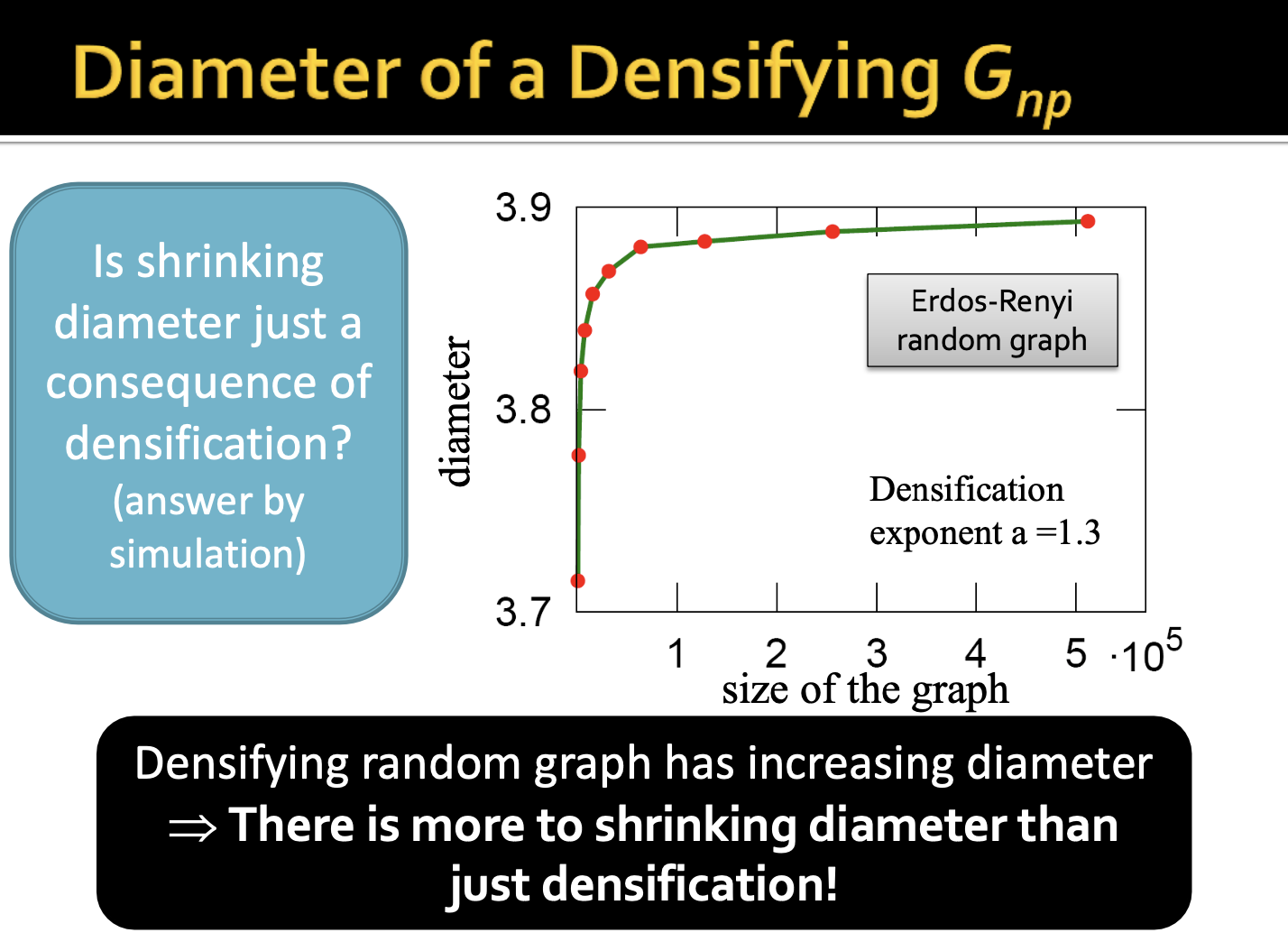
그렇다면 직경의 감소는 그저 밀도로 인한 결과라고 할 수 있을까요? 시뮬레이션을 통해 답을 얻을 수 있었다고 합니다. 서로 다른 크기의 랜덤 그래프를 생성한 뒤에 밀도를 측정합니다. 결과를 살펴보면 네트워크의 크기(여기서는 밀도를 의미한다고 이해했습니다, densify)에 따른 직경의 증가는, densification exponent가 1.3으로 증가한다고 이해할 수 있습니다.

if the densification would be the sole contributor to the shrinking diameter, I should see the thing going down, but don't

만약 직경의 감소에 대한 원인으로 densification이라고 한다면 오히려 densification exponent가 1보다 작고 그래프가 감소해야하지만 그렇지 않습니다. 즉, 정리하자면 밀도만이 직경의 감소의 원인이라고 할 수 없으며, 분명 다른 원인이 있을 것입니다.

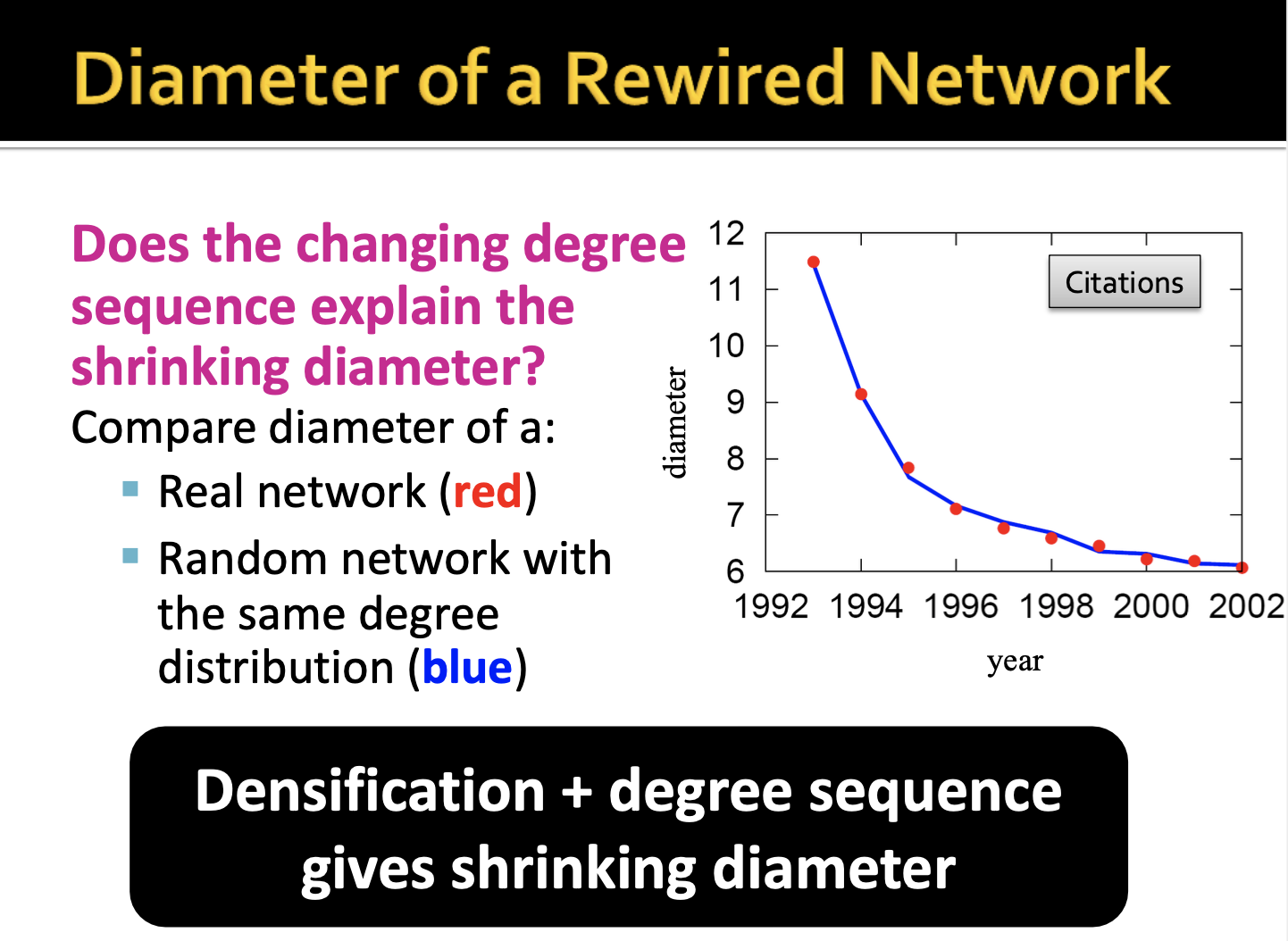
실제 네트워크와 같은 차수 분포를 가지는 랜덤 네트워크를 비교해봄으로써 직경의 감소에는 밀도와 degree sequence가 영향을 미쳤다는 것을 알 수 있었다고 합니다.

여기서 세번째 포인트 질문이 등장합니다.

네트워크의 차수의 분포(degree distribution)는 어떻게 변화하는가?

degree distribution은 어떻게 densification과 함께 진화할까요? 여기에는 degree sequence가 진화하는 2가지 방법이 있다고 합니다.

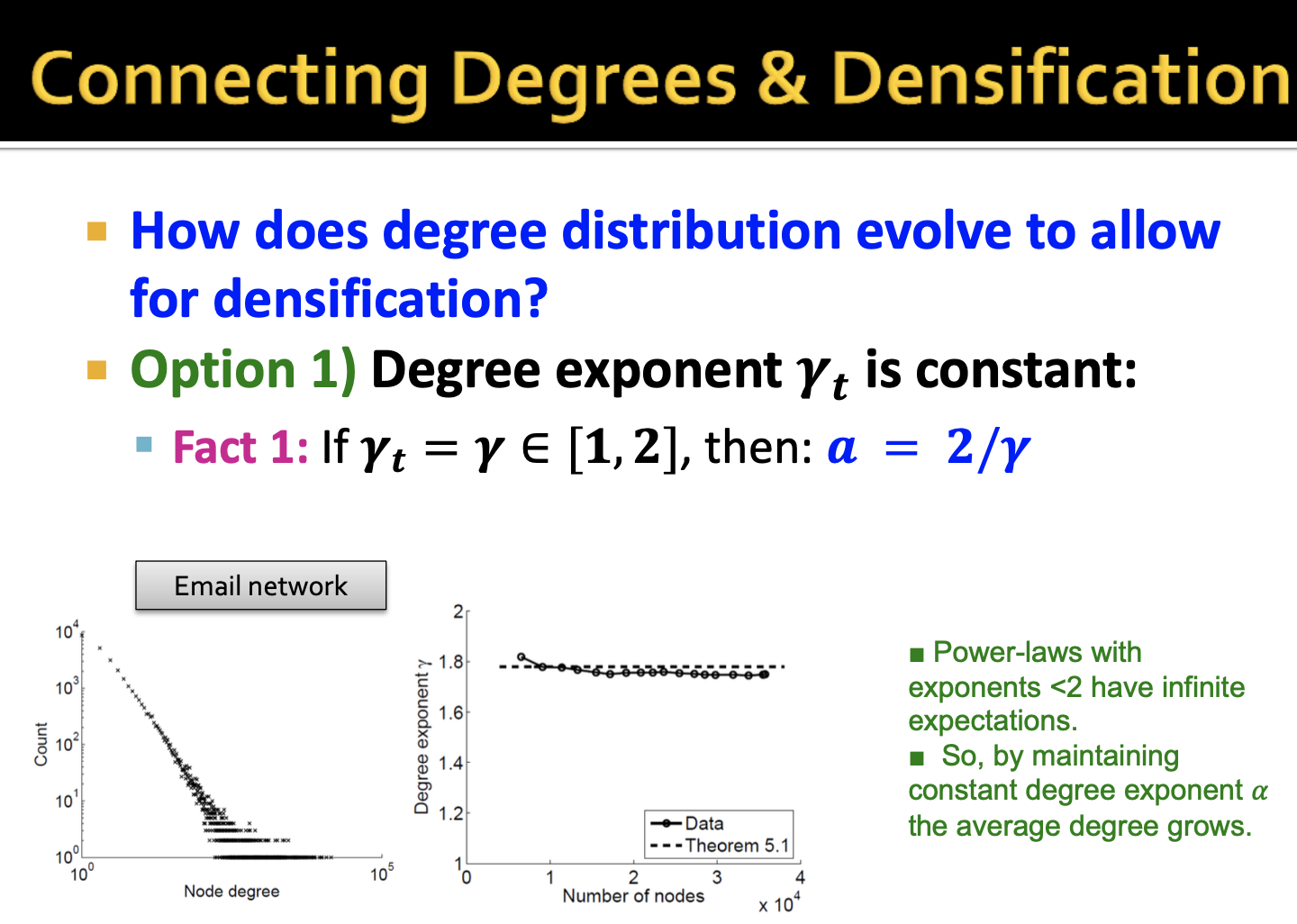
Option 1 where the degree exponent $\gamma_t$ is constant over time as network evolves. In this case if $\gamma_t = \gamma \in [1,2]$, then $\alpha = 2/\gamma$. Power laws with exponents less than 2 hav e infinite expectations, so by maintaining constant degree exponent $\gamma$ the average degree grows.

첫번째 방법은 네트워크 진화에 따른 degree exponent $\gamma_t$가 상수로 존재한다고 할 때, $\gamma_t$가 [1, 2] 사이의 값이라면 densification은 $2/\gamma$가 된다고 합니다. 솔직히 무슨 말인지 잘 모르겠습니다..

Email 네트워크 예시를 통해 알아보겠습니다. 해당 plot은 Email 네트워크의 degree distribution입니다. 노드의 차수와 그에 따른 노드 개수를 표현한 것이기에 분포도라고 할 수 있습니다. 정확하게 모든 것을 이해하지는 못했지만, 해당 plot에 대한 설명을 보자면, 먼저 차수가 낮은 노드의 개수 자체가 많은 것을 알 수 있는 반면 보통 차수가 많은 노드들의 분포가 많은 것을 알 수 있습니다. 이를 heavy-tailed라고 하는 것 같습니다. 또한 좌측 plot의 기울기(slope)에 대한 값을 $\gamma$라고 표현하는 것 같습니다.

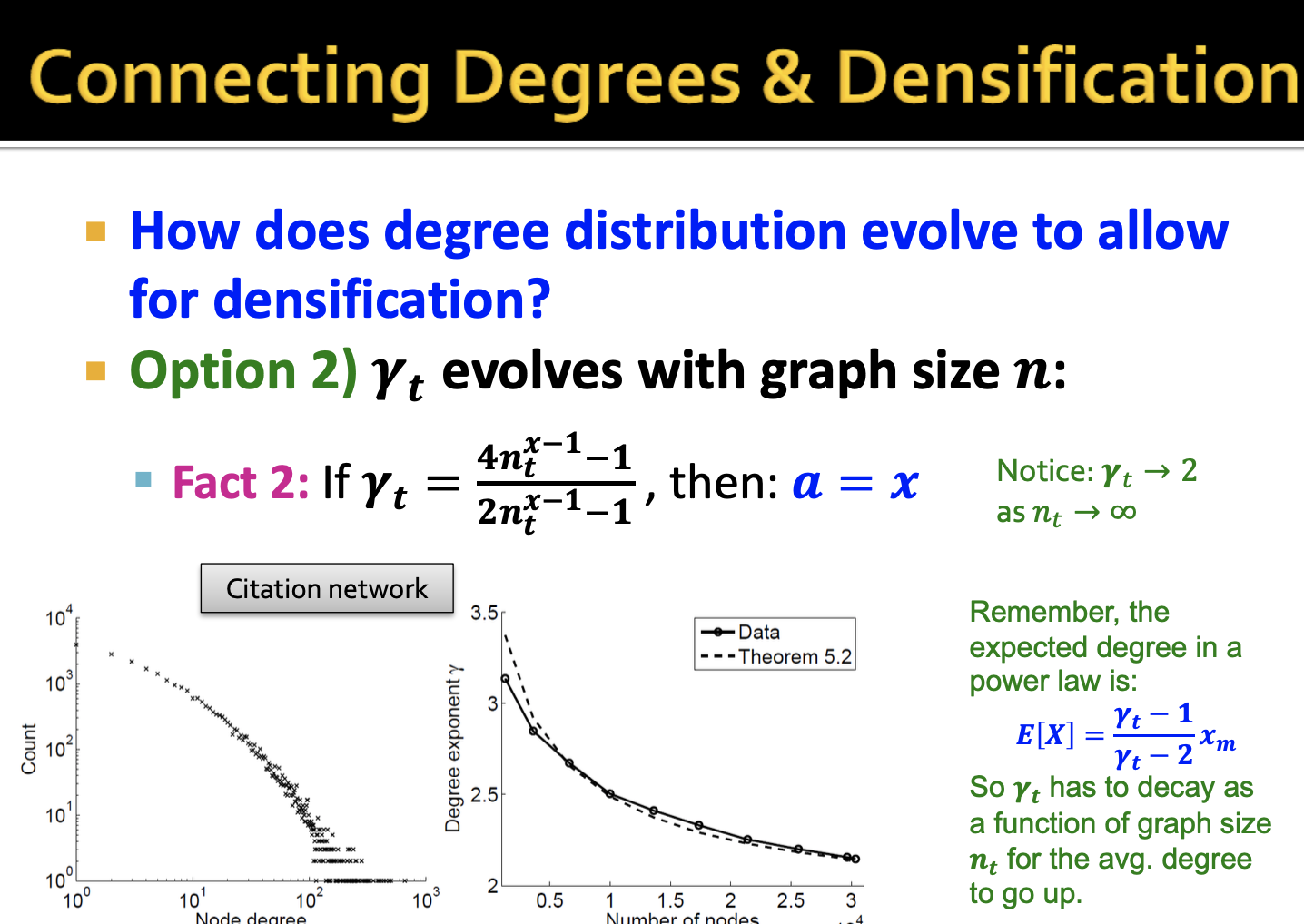
Option 2 where the degree exponent $\gamma_t$ evolves with graph size $n$, if $\gamma_t = \frac {4n^{x-1}_{t} - 1}{2n^{x-1}_{t} - 1}$ then $x = a$ the densifying constant. Here $\gamma_t -> \text {2 as }n_t -> \infty$. The expected degree in a power law is $E[X] = \frac {\gamma_t - 1}{\gamma_t - 2}x_m$, so $\gamma_t$ has to decay as a function of graph size $n_t$ for the average degree to go up.

결론적으로, 네트워크의 밀도가 높아지고 직경이 감소하는 현상에 대한 이유에는 degree distribution(차수의 분포도)가 시간에 따라 진화하고 either it's being basically having the distribution is constant and accoring to a given shape, that gives us densification.(뭔소리일까요..)

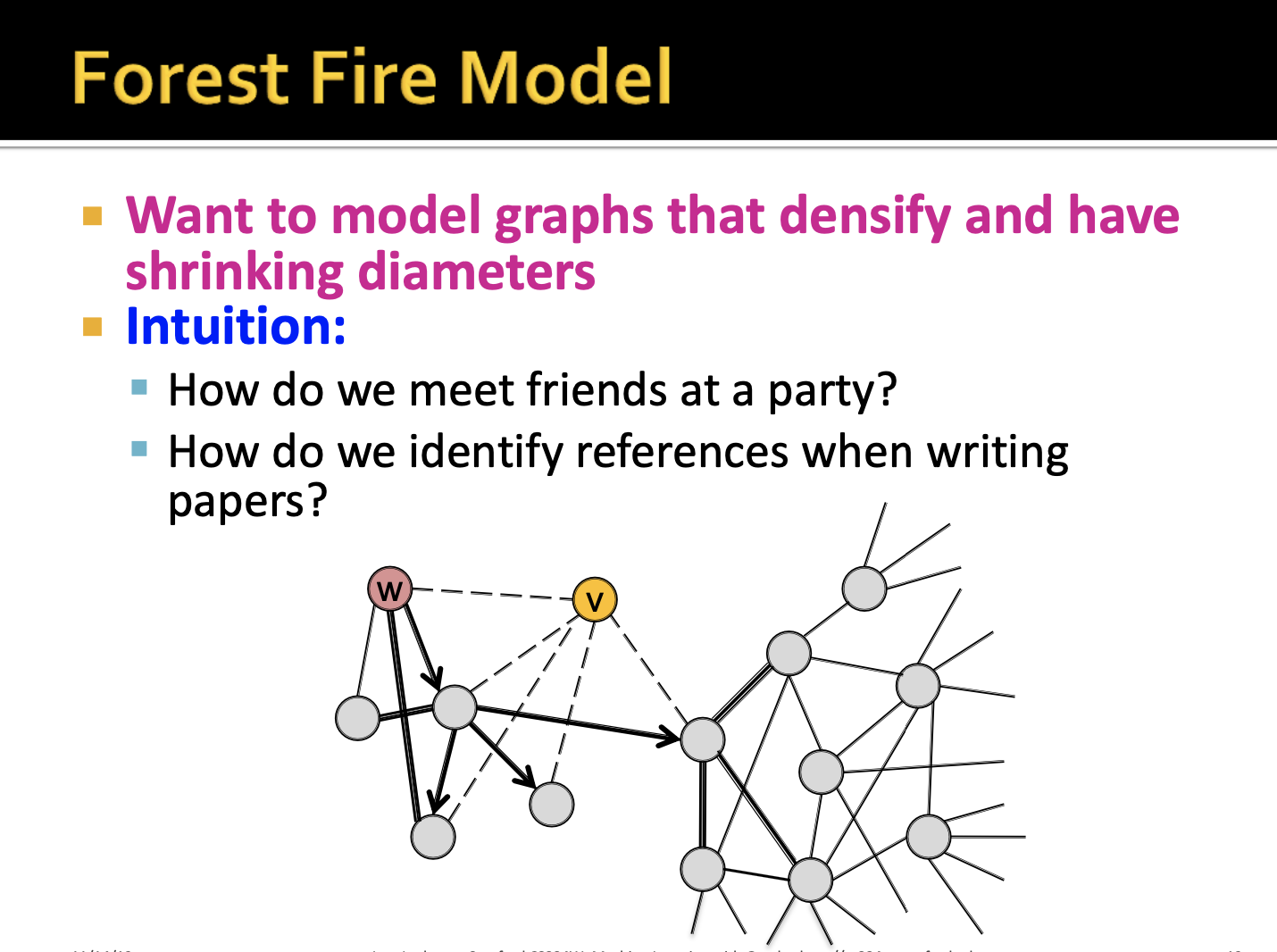
이러한 네트워크를 생성할 수 있는 Forest Fire Model에 대해서 소개합니다. 여기서 이러한 네트워크는 밀도가 높아지면서 직경이 감소하는 그래프를 말하는 것 같습니다.(graphs that densify and have shrinking diameters)

그래프가 진화하는 과정을 파티에서 친구를 만나 관계가 확장되는 것으로 예시를 들게 됩니다. 친구가 하나도 없던 v가 w라는 친구를 만남으로써 w의 친구들을 계속해서 소개받음으로써 친구 관계를 생성해나간다고 합니다. 여기서 w의 친구를 소개받고 w의 친구의 친구를 소개 받는 것을 fire spreads라고 표현합니다. 이 때, w의 친구를 모두 소개하는(spread) 과정을 가지는 것이 아니라 decide to spread it 과정을 가지는 것 같습니다.(어떤 기준인지에 대해서는 언급하지 않습니다.) 그리고 fire dies할 때까지 (소개할 친구가 없을 때까지) 이러한 과정이 반복됩니다.

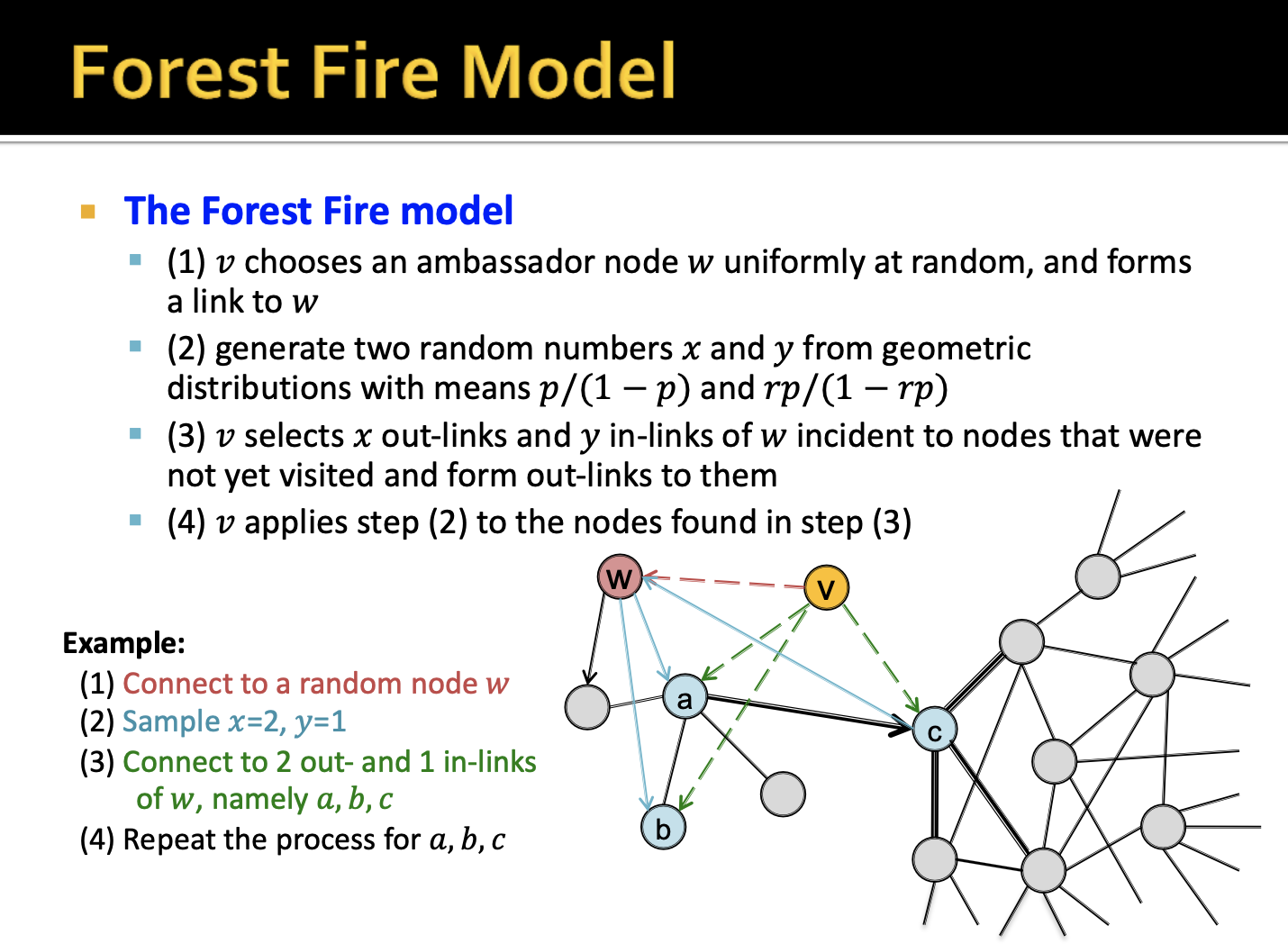
해당 과정에서는 forward burning probability, $p$ 와 backward burning probability, $r$ 이라는 2가지 파라미터가 필요합니다. 방향성이 존재하는 graph에서 새로운 v가 추가될 때마다 무작위로 'ambassador' 노드를 선택하게 됩니다.(ambassador 노드는 불을 번지게 하는 첫번째 노드 w를 의미하는 것 같습니다.)

다음으로 파라미터 $p, r$에 기반하여 spread할 노드의 in/out을 결정하는 binary 과정을 통해 최종적으로 몇 개의 노드에 fire spread할 지 결정하게 됩니다. 새롭게 spread한 노드에 대해서 다음 과정을 반복하면서 fire dies될 때까지 진행되며 새로운 노드 v는 fire spread된 모든 노드와 연결되게 됩니다.

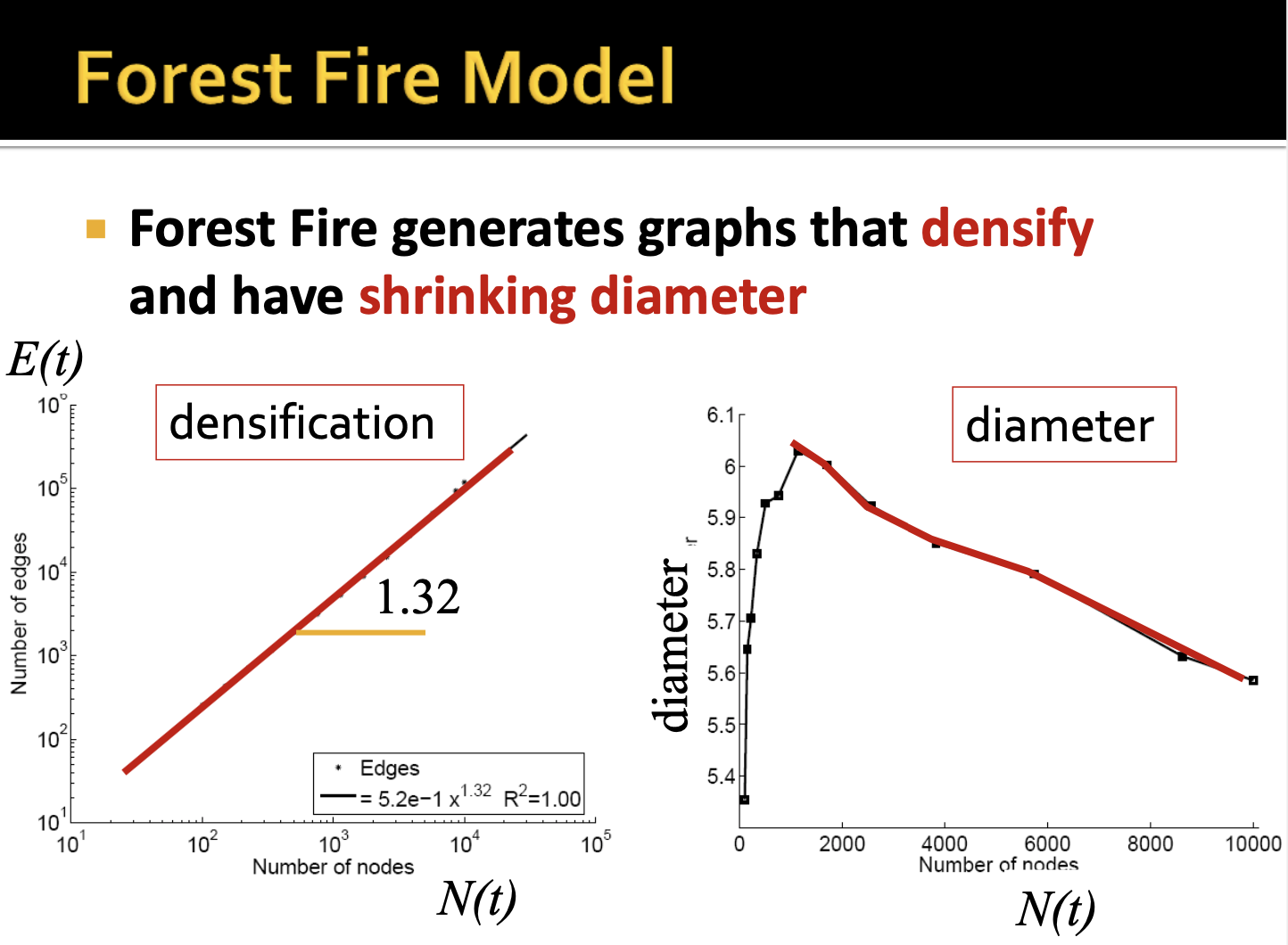
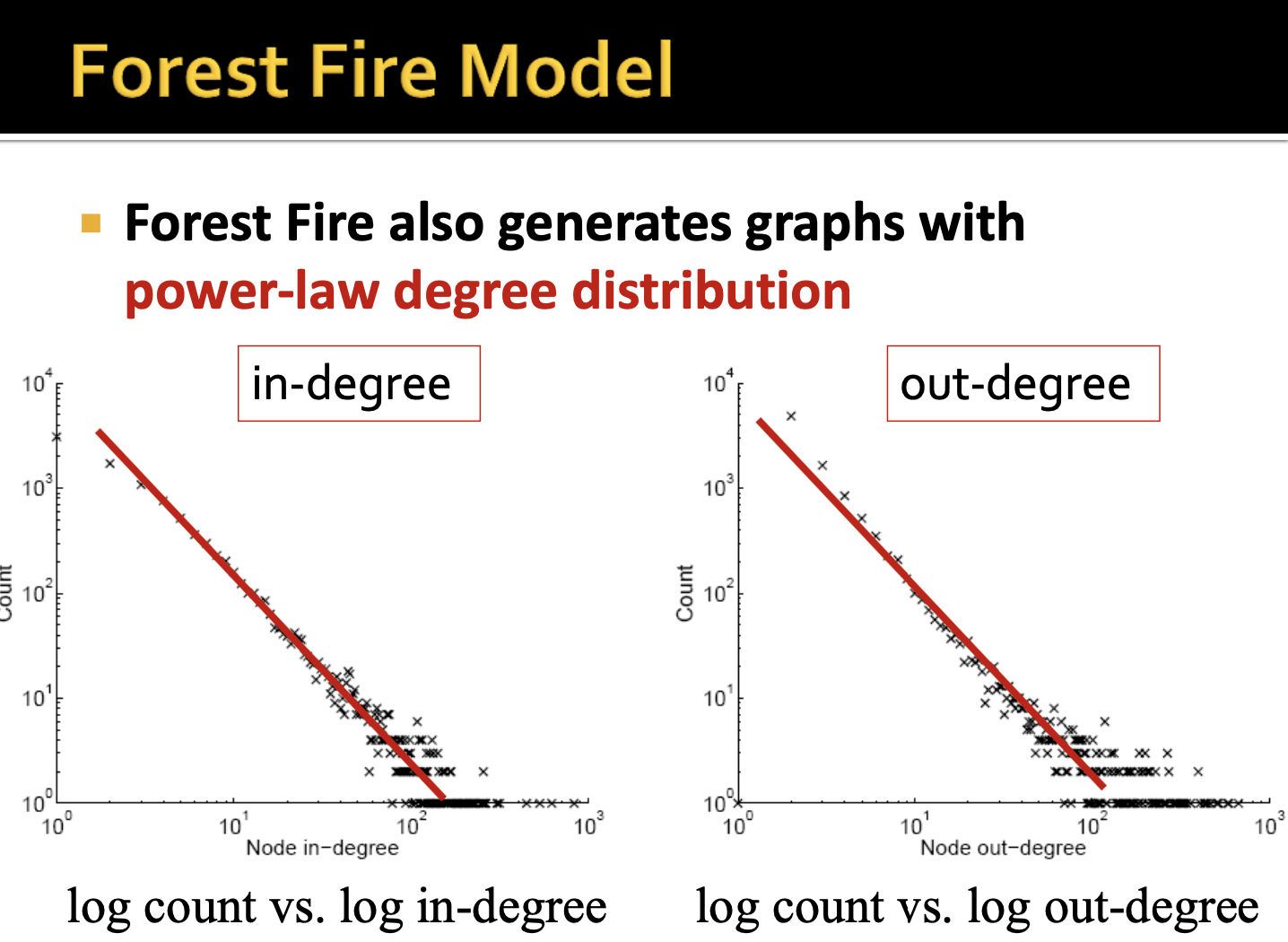
Forest Fire Model로 생성된 노드의 개수와 엣지의 개수를 로그 스케일상에서 살펴보면, densification exponent는 1.32가 나오게 되며 노드 개수가 증가함에 따라 직경이 감소하다는 것을 알 수 있게 됩니다.

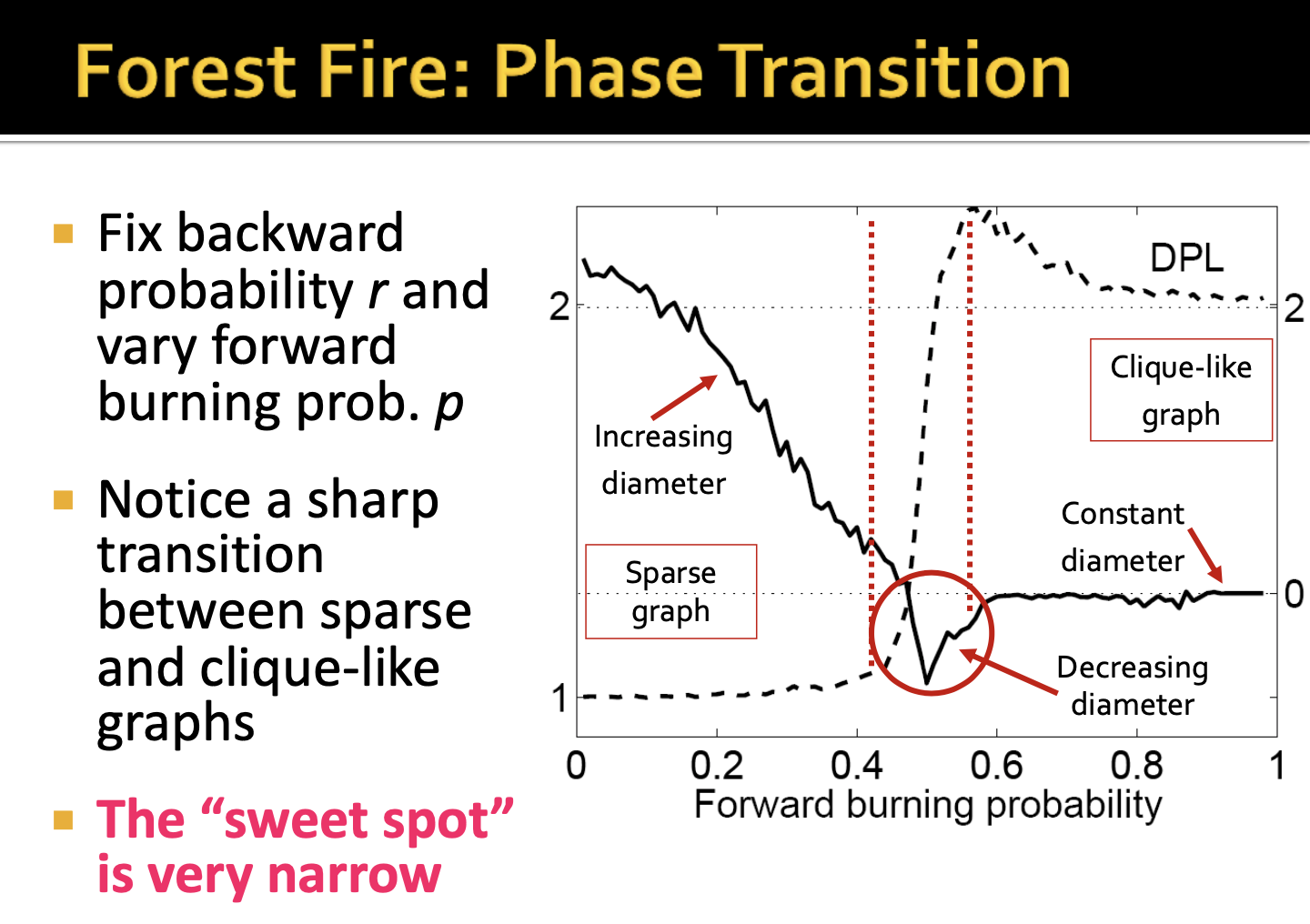
위 그림은 Forward burning probability, $p$에 대한 computational 과정에 대한 것입니다. $p$가 작게되면 fire spread를 위한 burning이 작으며, 크게 되면 많은 노드들을 burning하는 것으로 이해할 수 있습니다. 점선은 densification에 대한 변화를 의미하며 $p$가 작을 시에는 적은 관계가 형성되기 때문에 densification 또한 거의 없다고 볼 수 있습니다.

그래프의 지름의 경우에는 처음에는 증가하는 현상을 보입니다. 이렇게 되는 이유는 노드 간의 엣지(연결)이 dense하지 않고 sparse하기 때문에 한 노드에서 노드로 갈 수 있는 거리가 굉장히 멀기 때문입니다. 하지만 어느 시점에서는 diameter가 감소하게 되는데, 노드 간의 연결이 많아졌기 때문에 이제는 노드에서 노드로 갈 수 있는 거리가 가까워졌음을 의미합니다. 그리고 diameter가 일정하게 유지되는 이유를 complete graph라고 하는데 모든 노드간의 연결이 존재하기 때문으로 이해했습니다.

3. Temporal Networks

지금까지 살펴본 macroscopic level에서의 graph evolve는 어떠한 기준의 주기의 snapshot을 통해 변화를 살펴볼 수 있었습니다.

What we will do now is how nodes and edges are coming and leaving.

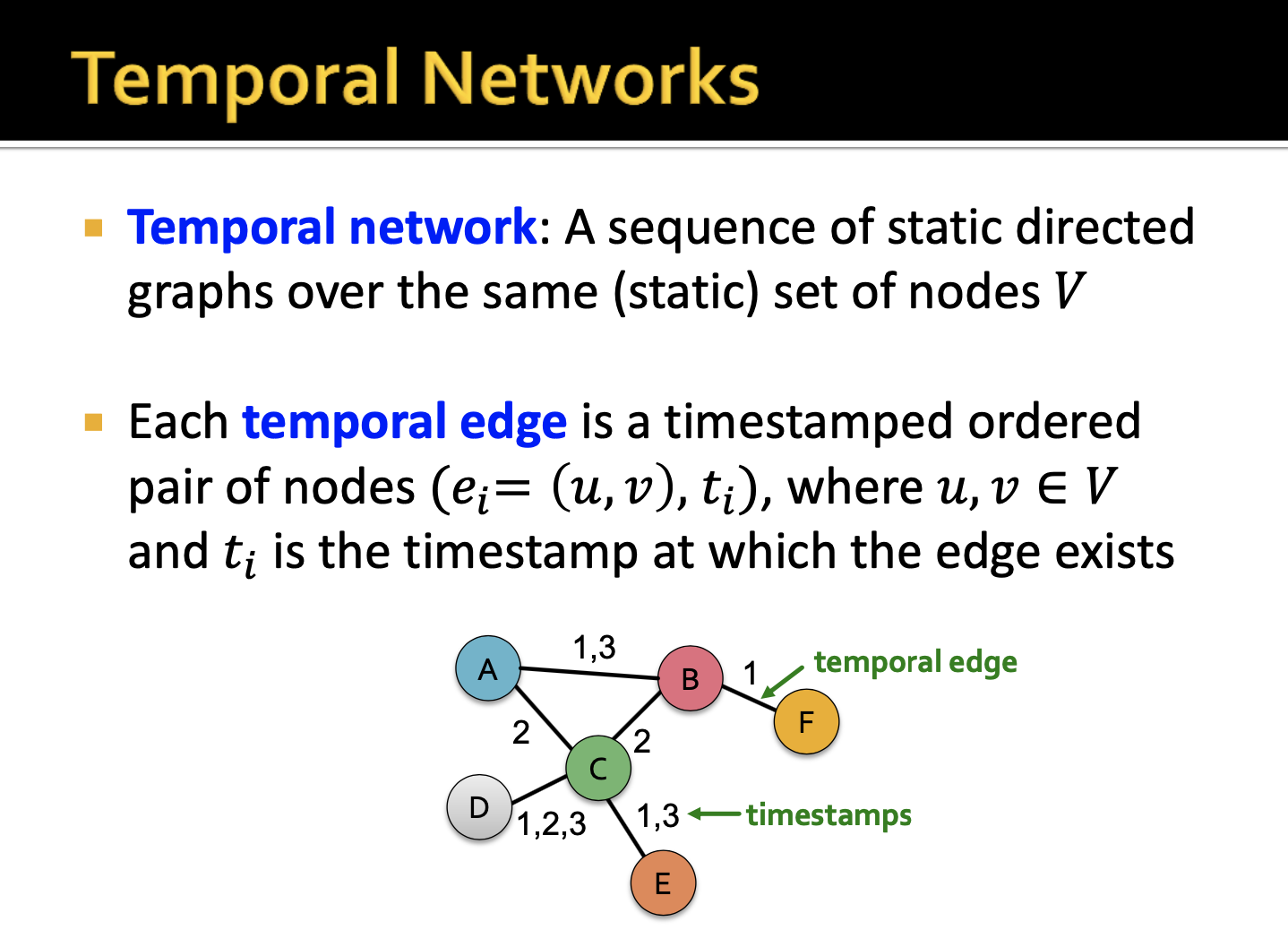
이번 목차에서는 어떻게 노드와 엣지가 추가되고 삭제되는지 알아보는 것 같습니다. 이 때 temporal networks를 정의하게 되는데, temporal networks란 동일한 집합의 정적 그래프의 연속?변화?입니다. 노드와 노드의 엣지에는 timestamp가 존재한다고 합니다. 이 timestamp가 연속에 대한 order를 의미하는 것 같습니다.

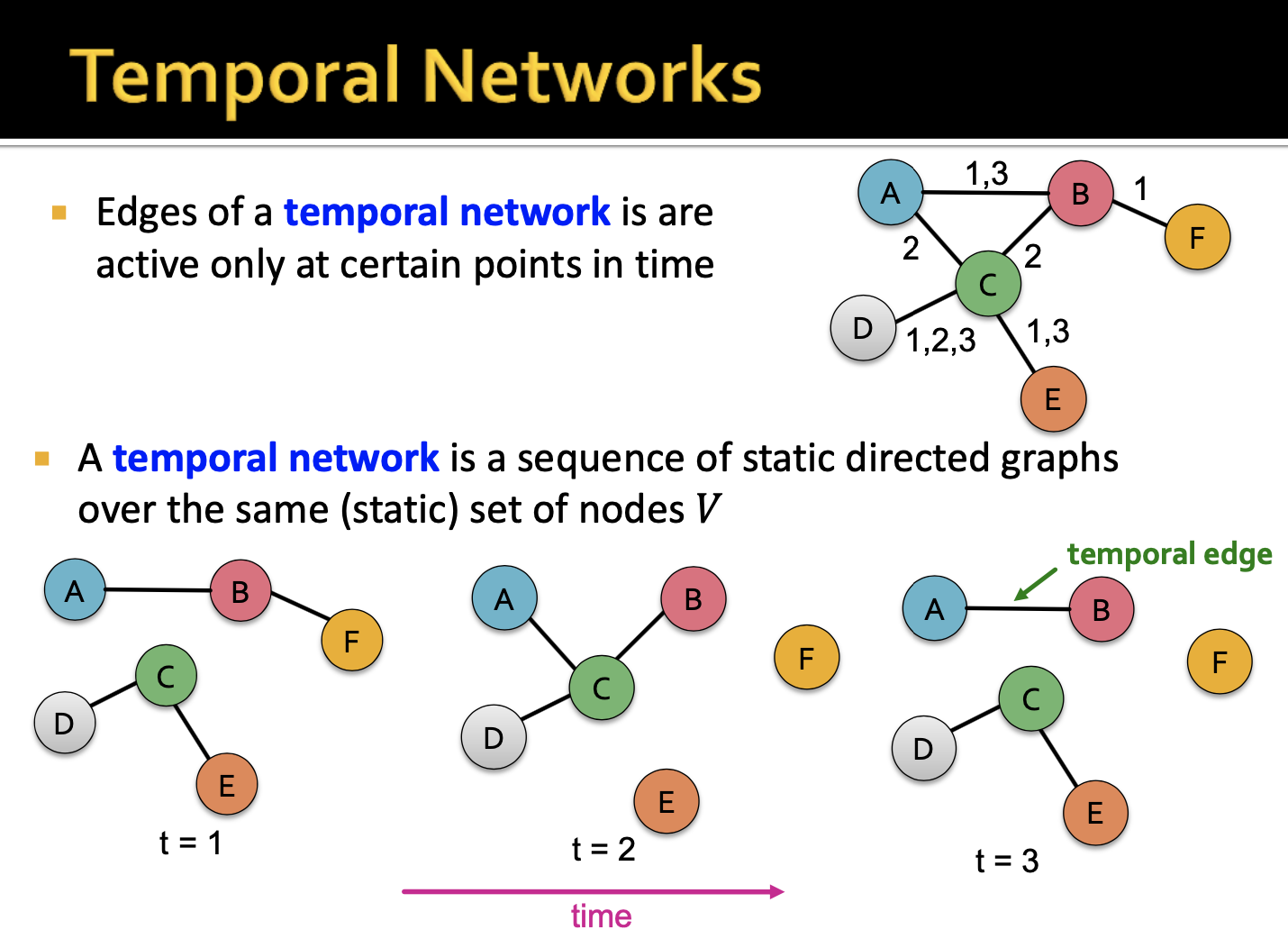
해당 네트워크를 보면 모두 같은 노드의 집합임을 알 수 있습니다. 그리고 time이 지날 수록 엣지가 변화하는 것 또한 볼 수 있습니다. 시점 1,2,3에 대한 snapshop을 통해 엣지가 변화하는 것을 볼 수 있는데, 엣지 (c,d)의 경우에는 시점 1,2,3에 모두 존재하기 때문에 최종 네트워크에서 엣지 (c,d)가 가지는 timestamp는 1,2,3이 됩니다.

temporal network의 예시로는 다음과 같습니다.

• communication networks like phone calls
• proximity networks like people in the same hospital room, meeting at a conference
• Transportation networks like trains or planes fly
• Cell biology networks like protein-protein interactions, gene regulation and etc

또한 하단의 그림은 일주일간 24시간 동안의 email communication에 대한 temporal network입니다. 그리고 하단 우측의 그림은 각 요일의 그래프를 집계한 것으로 이해했으며 이메일을 주고 받은 2명 간의 엣지가 표현되었습니다.

4. Microscopic Evolution of Networks

we can now start thinking about how do networks evolve at this microscopic level. how do the nodes change over time.

이번 목차에서는 microscopic level에서 네트워크가 진화하는 과정과 어떻게 노드들이 변화하는지에 대해 다뤄보고자 합니다. micro level에서 네트워크는 어떻게 진화할까요? macro level에서도 알아봤듯이, micro level에서도 질문의 포인트에 있어 2가지 question을 던집니다.

• How do we define paths and walks in temporal networks?, 어떻게 temporal networks에서 path(경로)와 walk(보행)을 정의할 것인가?
• How can we extend network centrality measures to temporal networks?, 어떻게 network centrality measures like PageRank or node importance를 temporal networks로 확장할 수 있는가?

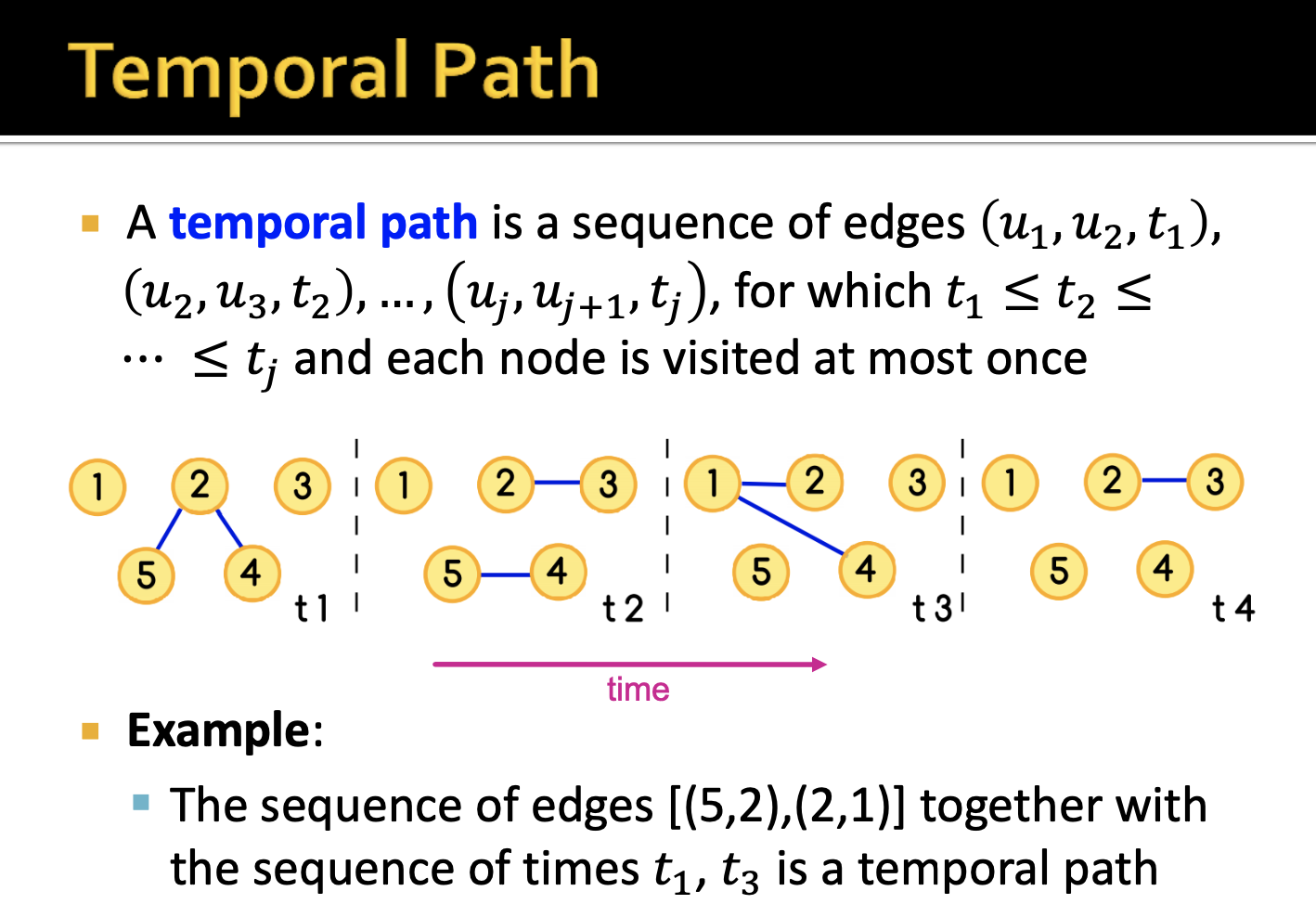
먼저 walk(보행), path(경로)에 대해 정의하고 그 개념들을 simple graph에서 temporal graph로 확장시킬 수 있습니다.

temporal path 또한 temporal network에서 이해했듯이, 시점마다 존재하는(sequential) 엣지들의 집합?이라고 할 수 있을 같습니다. 예시를 보자면, path (5, 1)이 만족하기 위해서는 시점 $t_1, t_3$의 temporal path이 필요하게 됩니다.

사실 이렇게 temporal path를 정의하는 이유를 정확히 이해하지는 못했지만 단순 그래프에서 경로를 계산할 때와, 시점이 존재할 때에 경로를 계산하는 것이 다른 결과를 초래하기 때문에 이처럼 시계열적인 특징을 고려하기 위해서 temporal path를 정의하는 것으로 이해했습니다.

그리고 TPSP-Djikstra algotirhm을 통해 가장 짧은 temporal path를 찾을 수 있다고 합니다.

해당 알고리즘의 예시를 한번 볼 수 있습니다. 총 5개의 시점으로 이루어진 해당 그래프는 시점 마다 엣지의 관계가 변하고 있음을 알 수 있습니다. 해당 그래프에서 각 시점마다 $path(a, f)$를 찾을 수 있습니다.

• $t_1: a-c-d-e-f$
• $t_2: a-c-d-f$
• $t_3: a-c-d-g-f$
• $t_4: a-b-g-f$
• $t_5: a-b-g-f$

이렇게 가장 짧은 경로를 구하는 알고리즘을 적용하는 이유는 closeness centrality 때문입니다. Temporal closeness는 시점마다 네트워크의 특정 노드와 모든 노드 간의 근접도 측정 방식입니다. 노드 간의 거리를 측정하게 되면 해당 노드가 네트워크의 중심부에 있는지 가장자리에 있는지 추측할 수 있습니다. 이 과정이 어떻게 보면 node importance, 노드의 중요성에 대해 판단할 수 있는 요소가 될 수 있습니다.

수식을 살펴보면, 주어진 시점에서 노트 x와 모든 노드 y들 간의 shortest path를 계산하여 합함으로써 closeness centrality를 구할 수 있습니다. 즉 closeness centrality가 1에 가까울수록 네트워크의 중심부라고 해석할 수 있을 것 같습니다.

example을 보게 되면 이해가 되지 않는 부분이 있었습니다. $c_clos(A, 2)$를 구하기 위해서 A와 C의 $t_2$의 distance가 1임을 알 수 있지만 A와 E의 $t_2$의 distnace가 왜 2가 나오는지 모르겠습니다. $t_2$에서는 path (A, E)가 성립되지 않는 것으로 이해했는데, 절대적인 path (A, E)라서 2가 더해지는 것인지 정확히 이해할 수 없었습니다. 아.. 혹시 path (A, B)와 path (A, E)가 $t_1$에 이미 만족하고 있기 때문에 성립되는 것인지 갑자기 생각이 들긴합니다. 확실하지는 않습니다.

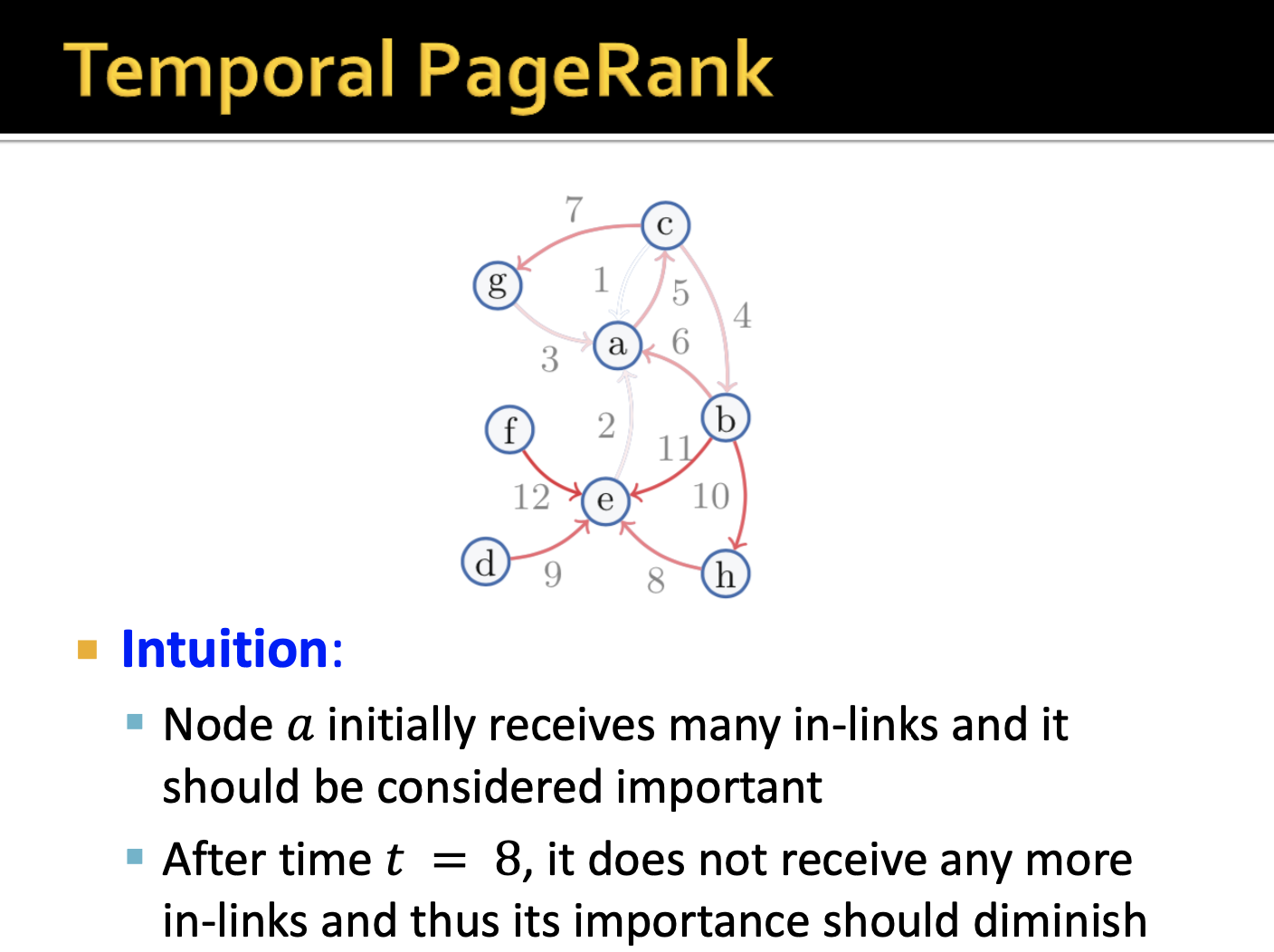
이 전 강의에서 페이지와 페이지가 연결되어 있는 인터넷 구조에서 페이지(노드)의 중요성을 판단하기 위해서 PageRank 알고리즘을 적용할 수 있었습니다. 사실 이 알고리즘에서도 temporal(시계열적)인 특징을 적용해볼 수 있습니다. 시간의 흐름에 따라 페이지와 페이지의 연결이 생기기도하고 사라지기도 하면서 해당 페이지의 중요도가 바뀔 수 있기 때문입니다.

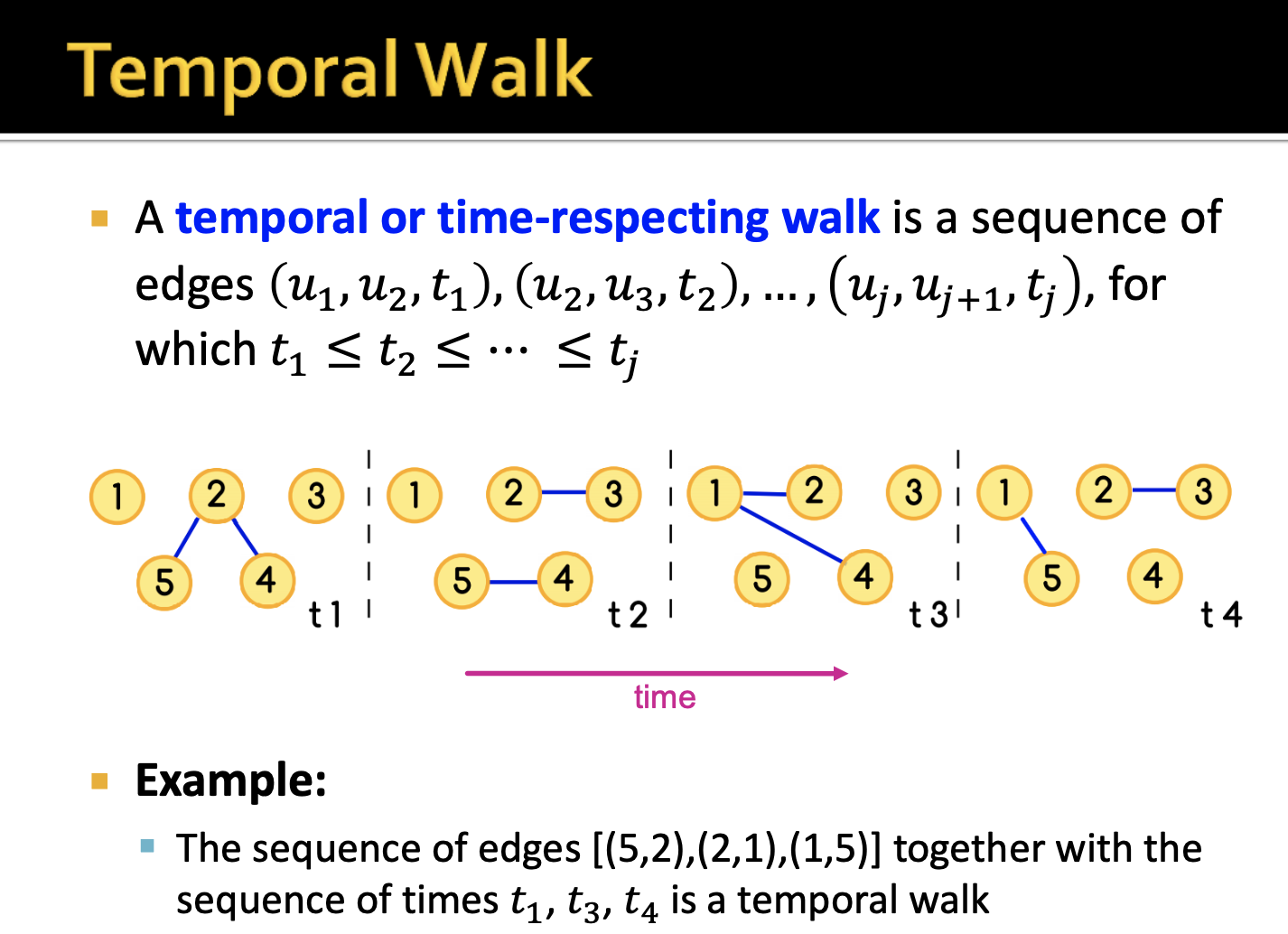
이번에는 temporal walk에 대한 개념을 정의해보도록 하겠습니다. 사실 해당 슬라이드의 설명으로는 temporal walk에 대한 개념을 이해하지 못했습니다.

해당 페이지랭크의 예시를 보면 time-respecting의 의미를 조금은 이해할 수 있었습니다. path (c -> b -> a -> c) 의 경우에는 엣지에 존재하는 timestamp가 시계열 특징을 만족하는 반면 path (a -> c -> b -> a)는 시점의 순서가 얽혀 time respecting 하지 못한다고 합니다.

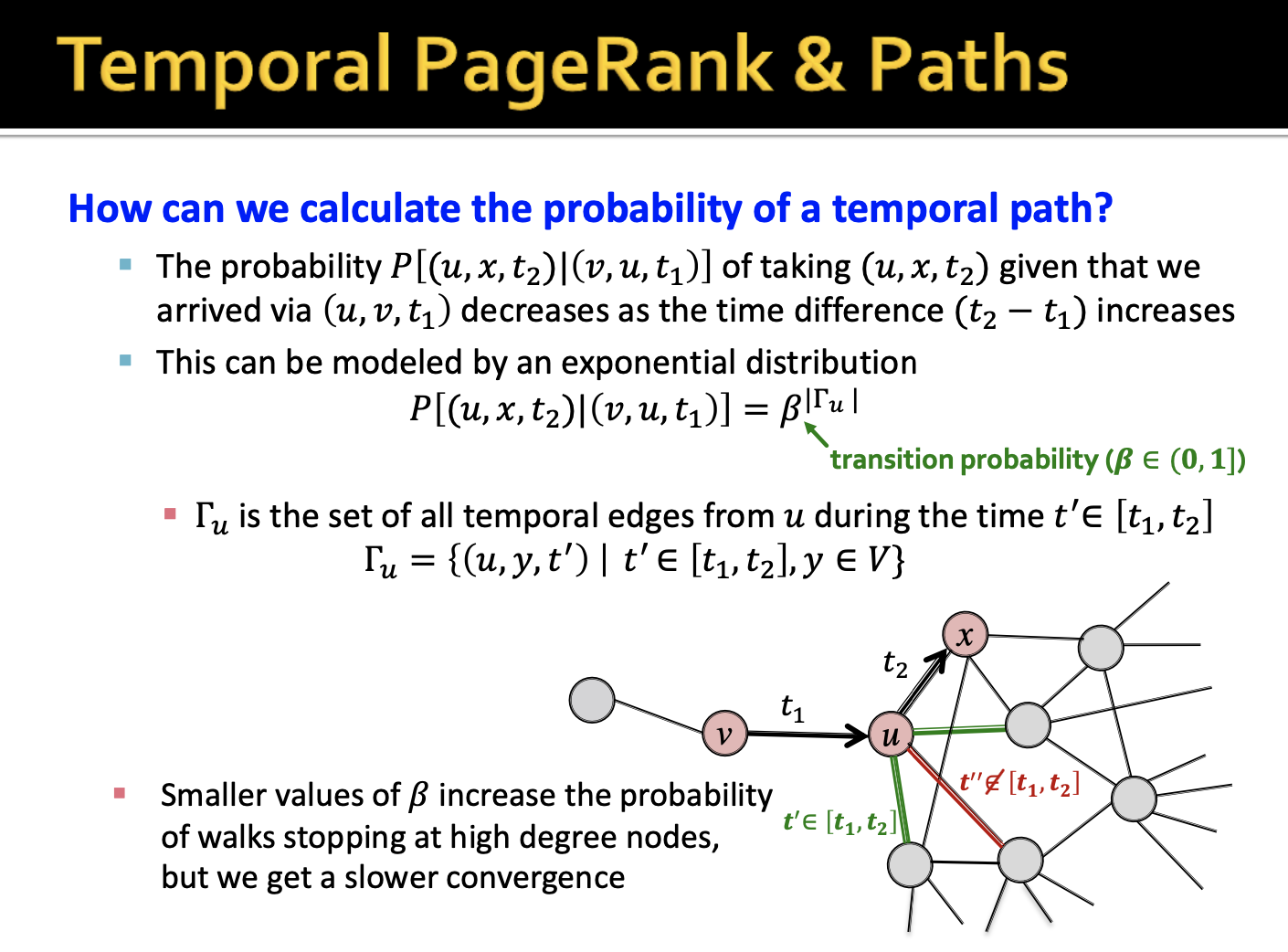
그렇다면 temporal path의 확률에 대해 생각해볼 수 있습니다.

$P[(u,x,t_2)|(v,u,t_1)]$

는 $t_1$시점에서 노드 v가 노드 u와 연결되어 있을 때, $t_2$시점에 노드 u가 노드 x와 연결될 확률을 의미합니다. 지수 분포 상에서 해당 확률을 정의하게 되면 다음과 같습니다.

$P[(u,x,t_2)|(v,u,t_1)] = \beta^{|Γ_u|}$

이 때, $\beta$는 transition probability로 0~1 의 값을 가지게 되며, $Γ_ u$는 해당 시점에서 노드 u가 가지는 엣지의 개수라고 할 수 있습니다. 그렇기 때문에 많은 노드와 연결되어 있는 엣지의 개수가 많아지게 되면 결국 특정 노드와의 연결 확률이 낮아지는 결과를 낳게 됩니다.

그런데 t 시점에 대한 제한이 없을 경우에는 temporal PageRank는 static PageRank에 수렴하게 됩니다. 이렇게 되는 이유는 결국 $t_1 - t_\infty$에서 발생하는 네트워크의 변화에 대한 축적이 static PageRank에서 다루는 완성된 네트워크와 동일하다고 볼 수 있기 때문으로 이해했습니다.

참고문헌

• Anil, 16.Network Evolution
• Tobigs graph study, Chapter16. network evolution graph