작성자 : 신민정

Contents

0. Intro
1. Embedding Nodes
2. Random Walk Approaches to Node Embeddings
3. Translating Embeddings for Modeling Multi-relation Data
4. Embedding Entire Graphs

0.Intro

이번 강의는 graph domain에서의 representation learning에 대해 알아보겠습니다.

representation learning이란, 어떤 task를 수행하기에 적절하게 데이터의 representation을 변형하는 방법을 학습하는 것입니다. 즉 어떤 task를 더 쉽게 수행할 수 있는 표현을 만드는 것입니다. Raw data에 많은 feature engineering과정을 거치지 않고 데이터의 구조를 학습하는 것으로, 딥러닝 아키텍처의 핵심요소라고 할 수 있습니다. 입력 데이터의 최적의 representation을 결정해주고 이 잠재된 representation을 찾는 것을 representation learning 또는 feature learning이라고 부릅니다.

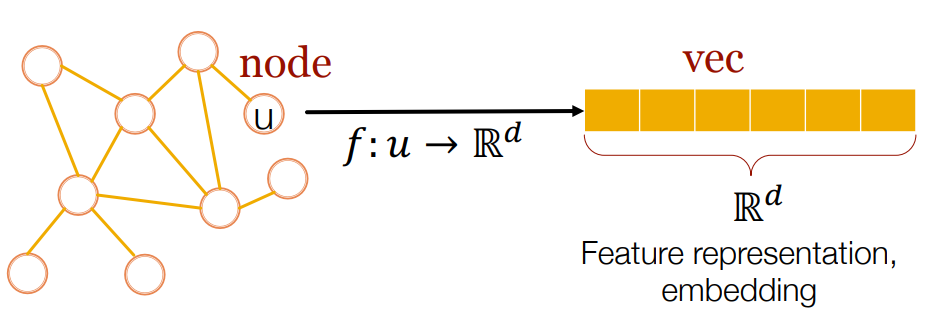
grpah에서의 representation learning 역시 같은 의미입니다.
graph의 node $u$를 mapping function $f$를 통해 Latent space(=embedding space)로 embedding할 수 있습니다. graph의 feature representation(=embedding)을 통해 다양한 task를 효과적으로 수행할 수 있습니다. 이때 효과적인 representation이란, task에 specific하지 않고 다양한 task에도 적용할 수 있는 representation을 의미합니다.




그렇다면 왜 graph를 Embedding해야 할까요??

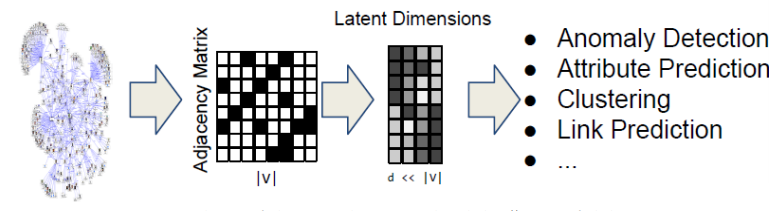
graph의 인접행렬(Adjacency Matrix)는 각 column이 node를 의미하기 때문에 sparse하고 크기 매우 큽니다. 인접행렬을 그대로 다루기에는 computation 측면에서 문제가 있습니다. 그렇기 때문에 grpah의 각 node를 low-dimension으로 mapping할 필요가 있습니다. Adjacency Matrix의 dimension보다 dimension이 낮은 Latent Dimension으로 embedding하여 computation의 효과를 얻을 수 있습니다. 각 node를 embedding하는 것이기 때문에 node별 representation이 가능합니다.
단, 각 column이 node를 나타내는 adjacency matirx와는 다르게, latent demension에서 나타낼 수 있는 embedding matrix의 column은 각 node를 나타내지는 않습니다. latent demension의 축들은 node가 아닌 node간의 상관관계와 같은 graph의 정보를 의미하는 feature가 됩니다. 즉, Adjacency matrix의 그래프 정보를 Latent Dimension으로 encoding하고, node representation을 만들어내는 것입니다.
graph의 정보를 담았기 때문에, latent space상에서 나타내지는 node간의 similarity은 실제 graph에서의 node간의 similarty라고 볼 수 있습니다.

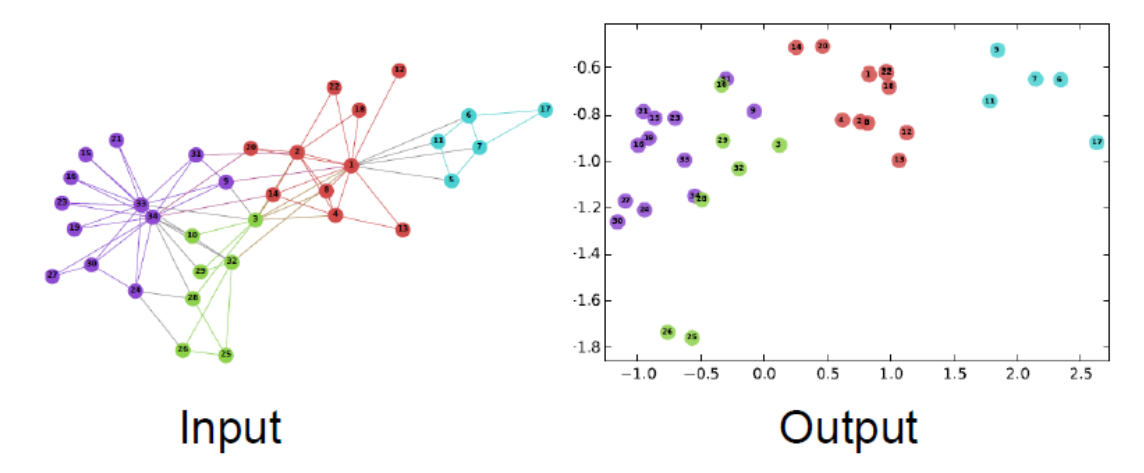
위 그림은 grpah를 2D latent space로 embedding한 예시입니다. 앞서 말씀드린것 처럼 각 node를 latent space에 mapping할 수 있고, latent space의 축은 node를 의미하는 것이 아닌 그래프의 정보를 담고있다고 이해할 수 있습니다.




그렇다면 기존 Deep Learning에서 사용하는 network들로 embedding을 할 수 있을까요??
결론부터 말씀드리자면 사용할 수 없습니다.
CNN은 고정된 크기의 이미지나 그리드에 적용할 수 있고, RNN이나 Word2Vec은 텍스트나 시퀀스 데이터에 적용됩니다.
하지만, graph는 이러한 데이터들보다 훨씬 복잡합니다. 이미지나 그리드처럼 특정 차원에 표현될 수 없고, 가끔 차원이 변동되고 multi-modal feature를 갖기도 합니다. 따라서 graph를 embedding하기 위해서는 graph만의 방식을 적용합니다.

2. Embedding Nodes

이제 graph의 node들을 embedding하는 방법에 대해 알아보겠습니다.

• graph $G$
• vertex set $V$
• adjacency matrix $A$ (assume binary)

node feature나 그 외 정보들은 사용되지 않습니다. (이하 Encoding은 Embedding과 같은 의미입니다.)

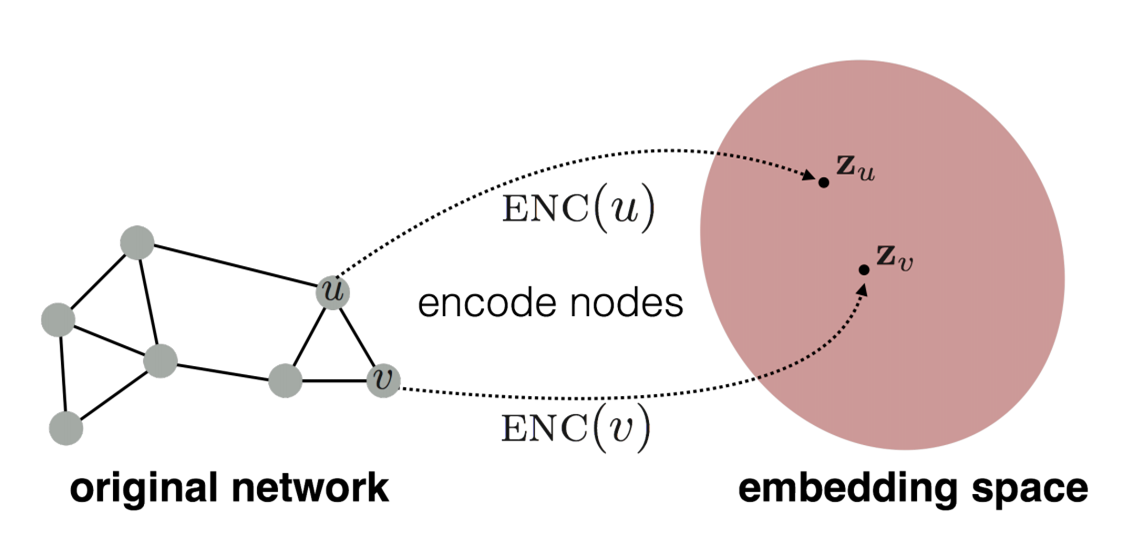
encoding의 목적은 embedding space상에서의 similarity와 원본 graph의 similarity최대한 동일하게 만드는 것입니다.
embedding space상의 두 vector의 similarity는 dot product $z_v^Tz_u$로 측정할 수 있습니다.

The dot product is proportional to both the cosine and the lengths of vectors.

과정은 다음과 같습니다.
1). Define encoder -> 각 node를 low-dimentional vecotr로 mapping(embedding)하는 방법 정의
$z_{node} = ENC(node)$
2). Define a node similarity function -> 원본 graph의 node간 유사도를 측정하는 함수를 정의
$similarity(u,v)$
3). Optimize the parameters of the encoder so that
$similarity(u,v) \approx z_v^Tz_u$

1) Encoder

Shallow Encoding

shallow encoder :encoding is just an embedding-lookup
$ENC(v)=Zv$

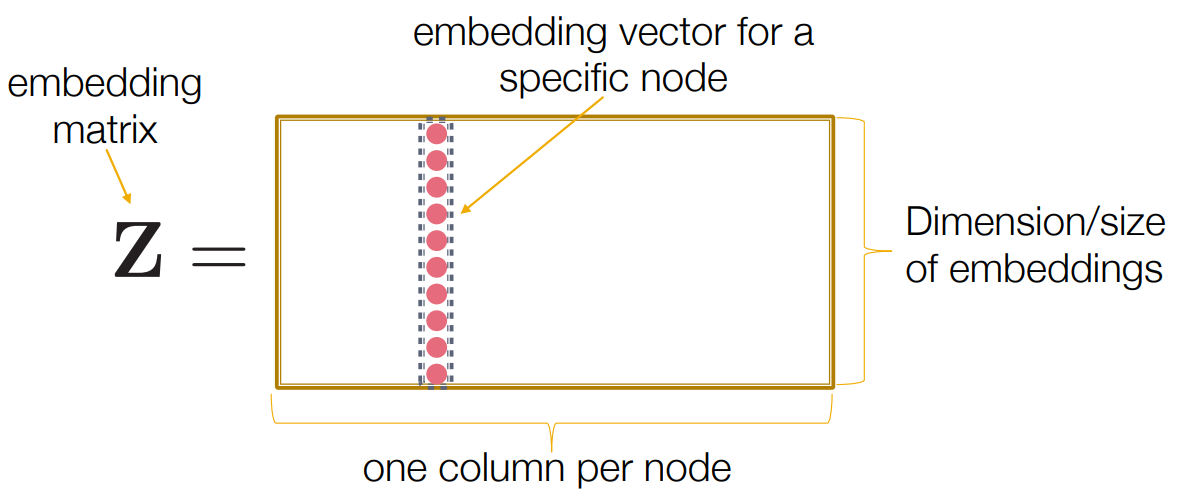
• $Z\in \mathbb{R}^{d\times|V|}$ : matrix. 각 column이 node embedding
• $v\in \mathbb{I}^{|V|}$ : indicator vector. node $v$를 지정하는 column과 만나는 element는 1, 그 외에는 0인 vector

$similarity(u,v) \approx z_v^Tz_u$을 optimize하며 $Z$를 학습시킵니다. shallow encoding으로 각 node를 개별적으로 representation할 수 있습니다.

shallow encoding 외에도 DeepWalk, node2vec,TransE등으로 Embedding할 수 있습니다.

다음 파트 2. Random Walk Approaches to Node Embeddings에서 상세히 다루겠습니다.

2) Similarity Function

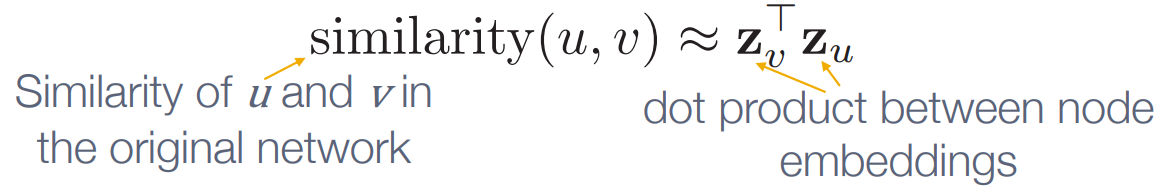
node similarity를 어떤기준으로 정의할지 결정해야 합니다. 예시는 다음과 같습니다.

• 두 노드의 연결관계
• 공유하는 node(neighbor)
• structural role의 유사성
• 등등

이 역시 encoding방법에 따른 similarity fucntion을 2. Random Walk Approaches to Node Embeddings에서 자세히 설명드리겠습니다.

3) Optimization도 2. Random Walk Approaches to Node Embeddings 에서 자세히 설명드리겠습니다. 강의 순서가 뒤죽박죽하군요

2. Random Walk Approaches to Node Embeddings

paper refenece :
Perozzi et al.2014 :DeepWalk: Online Learning of Social Representations
Grover et al.2016 : node2vec: Scalable Feature Learning for Networks

paper reference에서 알 수 있듯, DeepWalk, node2vec에 관련된 node embedding방법을 상세하게 다뤄보겠습니다.

Random Walk

Random Walk란, 말 그대로 node 위를 random하게 걸어다니는 것을 말합니다. 그래프의 특정한 시작점에서 random하게 neighbor들을 선택해서 나가는데, 그 point의 sequnce를 random walk라고 합니다. 걸어간 발자취를 나열한 것이라고 생각할 수 있습니다.

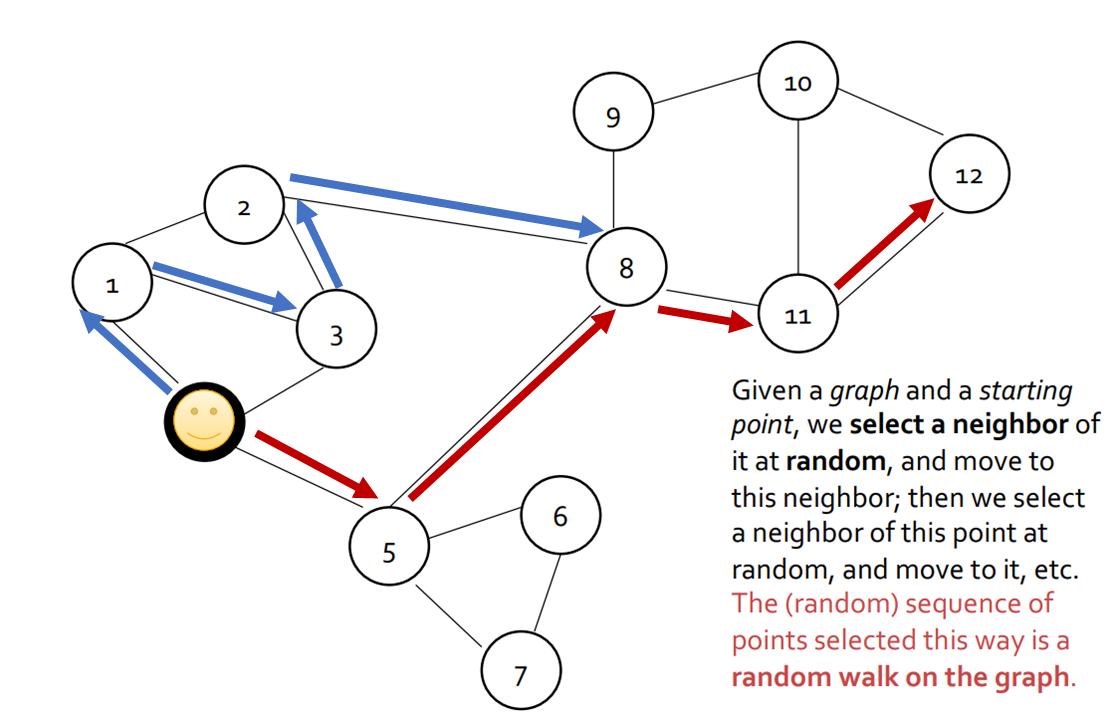
예를 들어, 위의 그림에서 노란색 point가 시작점으로 주어지고 4걸음을 간다는 parameter가 주어진다면 [1,3,2,8,11]이 random walk가 될 수 있습니다. 3걸음을 간다고하면 [5,8,11,12]가 될 수 있습니다.
이러한 random walk는 parameter를 주고 sampling한다고 표현합니다.

Random-walk Embedding (Deep Walk)

$z_u^Tz_v \approx$ probability that $u$ and $v$ co-occur on a random walk over the network

$z_u^Tz_v$를 "network 전체의 random walk에서 $u$와 $v$가 함께 발생할 확률"로 근사할 수 있습니다. 왜냐하면 $z_u$와 $z_v$의 similarity가 높다면 latent space상에 가깝게 위치할 것이고, 이는 node $u$와 $v$의 similarity가 높다는 의미이므로 random walk에서 동시에 발견될 확률이 높기 때문입니다.


Random-walk Embedding의 과정은 다음과 같습니다.

• 1.어떤 random walk strategy R을 사용하여 node u에서 출발하여 node v에 방문할 확률 $P_R(v|u)$ 을 추정합니다.
  
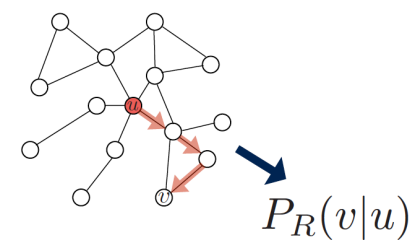
• 2. 이 $P_R(v|u)$를 encoding하기 위해 embedding을 최적화시킵니다.
     여기서 두 $z$의 similarity인 dot product는 $cos(\theta)$과 같고, 이는 random walk similarity로 볼 수 있습니다.
     
     
     
     
     
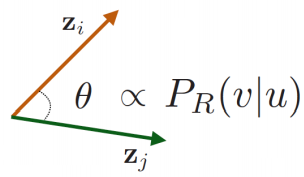
     그렇다면 왜 Random Walks를 사용할까요??
• Expressivity : Local과 Higher-order neighborhood 정보를 함께 고려하는 node similarity를 유동적으로 정의내릴 수 있습니다.
  한국어로 풀어쓰니까 의미전달이 직관적이지 않네요... 강의자료에는 "Flexible stochastic definition of node similarity that incorporates both local and higher-order neightborhood information"라고 명시되어있습니다.
• Efficiency : 학습할 때, 모든 node쌍을 고려할 필요 없이, 오직 random walk에 함께 발견될 쌍들만을 고려하면 됩니다.
  이는 그래프의 크기가 클수록 더 두드러지는 장점입니다. (ex. real social graph)
  
  
  
  

Random Walk Optimization

다시 graph domain에서의 Unsupervised Feature Learning의 의미를 생각해봅십다.
목표는 유사성을 보존하는 d-dimension의 latent space에서의 node embedding을 찾는 것이었습니다. 실제 graph에서 가깝다면 latent space상에서도 가깝도록 embedding해야 합니다.
그렇다면 node $u$가 주어질 때, node의 주변, neighbor를 어떻게 정의할 수 있을까요? 다음과 같이 정의됩니다.

$N_R(u)$ : random walk strategy $R$로부터 얻을 수 있는 $u$의 neighborhood

graph $G=(V,E)$가 있을 때, feature learning의 목표는 mapping function $z:u \rightarrow \mathbb{R}^d$를 학습하는 것입니다. 이때 Objective function은 다음과 같습니다.

Log-likelihood objective
$max_z \sum_{u \in V}^{}{logP(N_R(u)|z_u)}$
Given node $u$, we want to learn feature representations that are predictive of the
nodes in its neighborhood $N_R(u)$

node의 neighborhood를 예측하는 방향으로 feature representation을 학습합니다.

Random Walk의 Optimization 과정을 정리해보겠습니다.

Random Walk Optimization

• 1. graph의 각 node에서 정해진 짧은 길이만큼의 random walk를 수행합니다
     (using some strategy $R$)
• 2. 각 node의 neighborhood $N_R(u)$를 수집합니다.
     ($N_R(u)$ : the multiset of nodes visited on random walks starting from $u$)
• 3. node $u$가 주어질 때, 그 node의 neighborhood $N_R(u)$를 잘 예측하는 방향으로 node를 embedding합니다.
     $max_z \sum_{u \in V}^{}{logP(N_R(u)|z_u)}$

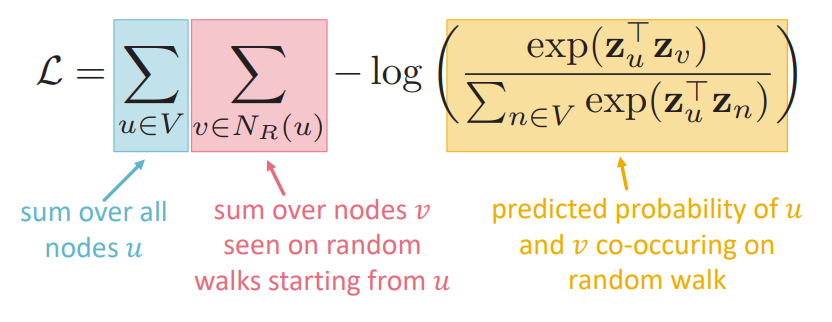
loss function
$L = \sum_{u \in V}\sum_{v \in N_R(u)}-log(P(v|z_u)$

intuition Random walk가 동시에 발생(co-occurrrence)할 likelihood를 maximize할 수 있도록 embedding을 최적화
이때 $p(v|z_u)$는 vector representation이 softmax를 거친 후의 값입니다.
$P(v|z_u) = {{exp(z_u^Tz_v)}\over{\sum_{u \in V}exp(z_u^Tz_v)}}$
softmax를 사용하는 이유는 node $u$와 가장 유사도가 높은 node $v$를 얻기 위함입니다.
$\sum_iexp(x_i) \approx max_iexp(x_i)$

Optimizing random walk embeddings =
Finding embeddings $z_u$ that minimize $L$
정리하면 위와 같습니다. grpah의 모든 node에 대해, 각 node의 neighborhood가 random walk시에 동시에 발견될 확률을 높도록 embedding을 학습합니다.

하지만, 이 naive한 과정은 compuation 측면에서 매우 expensive하다는 단점이 있습니다.

softmax의 normalization term $\sum_{u \in V}exp(z_u^Tz_v)$이 원인입니다. log안에 있는 ${exp(z_u^Tz_v)}\over{\sum_{u \in V}exp(z_u^Tz_v)}$부분을 근사하여 이 문제를 해결합니다. 이때 Negative Sampling이 사용됩니다.

Negative Sampling

위에서 설명한 loss fuction의 log안의 함수를 다음과 같이 근사합니다.

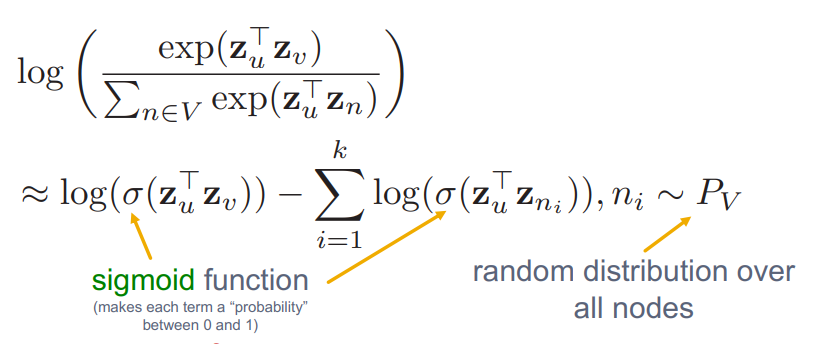
모든 node를 고려하여 normalize한 기존의 loss는 expensive했기 때문에, random으로 Negative sampling한 k개의 negative samples $n_i$에 대해서만 normalize합니다. w2v에서 전체 corpus에서 빈도가 높은 단어를 negative sample로 sampling하였듯이, node의 degree가 높은 node를 negative sample로 사용합니다.

negative sample의 개수 $k$가 갖는 의미는 다음과 같습니다.

• Higher $k$ gives more robust estimates
• Higher $k$ correspond to higher bias on negative events

실제로는 $k$는 5~20으로 설정합니다.



지금까지 randome walk로 node를 embedding하는 방법에 대해 알아보았습니다.
random walk는 지정한 시작점에서 고정된 길이 "fixed size"를 조건으로 시행됩니다. 하지만 이러한 조건때문에 한계가 있습니다.
만약, 두 노드의 structural role이 비슷하지만 멀리 떨어져있는 경우라면 어떨까요?? 실제로 두 node는 유사하지만, random walk는 고정된 사이즈로만 노드주변을 보기 때문에 random walk embdding방식으로는 이 유사성을 담지 못할것입니다. 이러한 경우 node의 similarity를 담도록 latent space에 embedding한다"라는 node embedding의 가장 큰 목적에 맞지 않습니다. 또한 random하게 보기 때문에, graph의 전체 structure를 고려하지 못한다는 단점도 있습니다.



이 단점을 보완한 node2vec에 대해 알아보겠습니다.

node2vec

Deep Walk의 단점을 보완한 node2vec에 대해 알아보겠습니다.
이 역시 graph의 node를 embedding하는 방식이기 때문에, node2vec의 목표는 다양한 task에 적용가능하도록 (downstream task에 상관없이) graph에서 node의 neighborhood간의 유사성을 latent space (feature space)상에서도 유지하는 것입니다. node2vec은 maximum likellihood optimization문제로 접근합니다.

Abstract
네트워크의 node와 edge에 대해서 prediction task를 수행하는 것은 feature engineering 측면에서 많은 노력이 소요된다. 최근의 연구들에서는 reprsentation learning 측면에서 feature 자체를 학습하여 이 측면에서 많은 혁신들이 있었으나, network에서 파악되는 connectivity pattern에 대해서는 제대로 학습하지 못한다는 한계를 가지고 있다. 따라서, 이를 해결하기 위해서 network의 이러한 feature를 학습할 수 있는 프레임워크인 node2vec을 제시하였다. node2vec에서는 network의 node들의 관계(neighborhood)를 우도(likelihood)를 최대화할 수 있는 low-dimensional(저차원) 피쳐 공간을 학습시켰다. 실제로 기존의 존재하는 데이터들을 대상으로 수행을 해봤는데 괜찮은 결과가 나왔다.

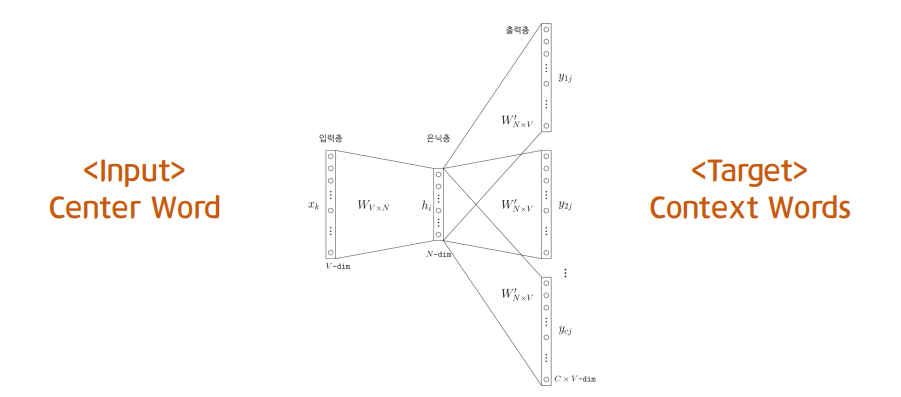
Recap : word2vec
여기에서 제가 제일 word2vec을 모르겠지만 감히 설명해볼게염...

• skipgram : 중심단어(center word)로 주변단어(context word)를 예측
  
  가정 : 실제 문장들에서 비슷한 위치에 있는 word들은 embedding space에서도 비슷한 위치에 있을것이다.
  따라서 중심단어(c)가 주어졌을 때 주변단어(o)가 나타날 확률(아래식)을 최대화 하면 됩니다.
  $P(o|c)= {{exp(u_o^Tv_c}\over{\sum_{w=1}{W}exp(u_w^Tv_c)}}$
  graph에서는 특정 node가 주어졌을 때 그 node의 neighborhood가 나타날 확률을 최대화 하면 되겠네요!

random하게 neighbor를 보아서 graph 전체 structure를 고려하지 못한 Deep Walk의 단점을 개선하기 위해, node2vec에서는 기존의 randomwalk를 사용하지 않습니다.

node2vec key idea
use flexible, biased random walk that can trade off between local and global views of the network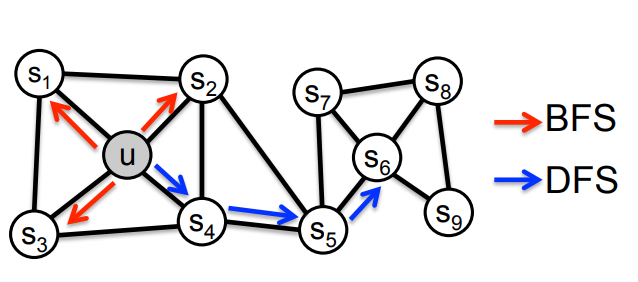

특정 node $u$의 neighborhood$N_R(u)$는 DFP와 BFS로 정의할 수 있습니다.

• $N_{BFS}(u)$ : local 영역으로 neighborhood 지정 (microscopic view)
  (위 그림 예시: if size of $N_{R}(u)$ = 3 $\rightarrow$ $N_{BFS}(u)={s_1,s_2,s_3}$)
• $N_{DFS}(u)$ : Global 영역으로 neighborhood 지정 (macroscopic view)
  (위 그림 예시: if size of $N_{R}(u)$ = 3 $\rightarrow$ $N_{DFS}(u)={s_4,s_5,s_6}$)

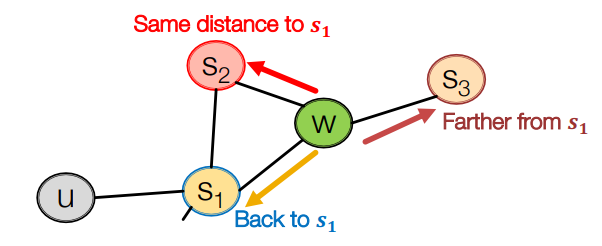
node2vec에서는 Biased 2nd-order random walk를 사용합니다.

• 1st-order random walk : node to node
• 2nd-order random walk : edge to edge

biased fixed-length random walk는 두가지 parameter를 정의해야 합니다.

• return parameter $p$ : 이전 node로 돌아갈 가능성을 계산하는 parameter. 주변을 잘 탐색하는지
  $p$가 낮을수록 BFS like walk (좁은 지역 고려)
• in-out parameter $q$ : DFS와 BFS의 비율. random walk가 얼마나 새로운 곳을 잘 탐색하는지
  $q$가 낮을수록 DFS like walk (넓은 지역 고려)

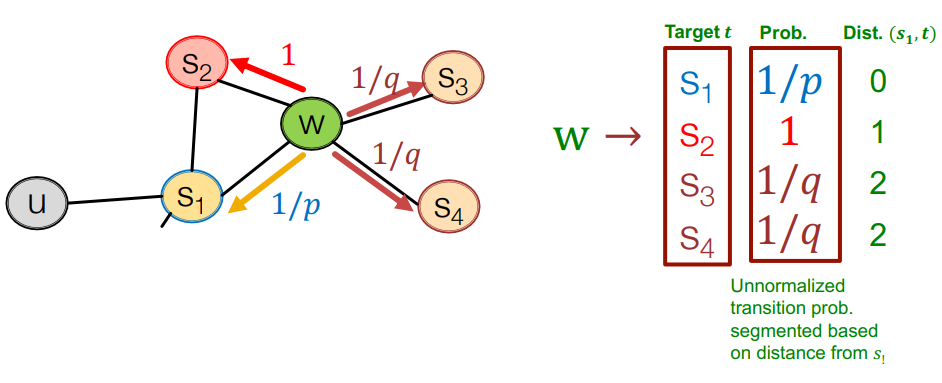
example
$(s_1,w)$의 경로로 이동하여 지금 $w$인 상태
node $w$의 neighborhood로 $s_1,s_2,s_3$만 가능합니다.
$s_2$는 $s_1$과 $w$의 공통 이웃,
$s_3,s_4$는 $s_1$으로부터 멀어지는 방향입니다.

$p$가 낮을 수록 좁은 지역을 보고 $q$가 낮을수록 넓은 지역을 봅니다.

node2vec algorithm

1. 예시와 같이 random walk probability를 계산합니다.
2. grpah의 각 node $u$에 대해 길이 $l$만큼의 random walk를 합니다.
3. node2vec을 SGD로 최적화합니다.

node embedding의 대표적인 두가지 방법 Deep Walk와 node2vec을 배워보았습니다. 이러한 embedding을 통해 graph의 정보를 최대한 보존하면서 computation 효과를 볼 수 있었습니다.
graph의 node $u_i$들을 latent space로 임베딩한 embedding vector $z_i$들은 어디에 사용될 수 있을까요??
기존 머신러닝에서 데이터를 임베딩(ex. 차원축소)하여 clustering, classification을 할 수 있듯 graph domain에서도 많은 task를 수행할 수 있습니다.

• Clustering / Community Detection
• Node classification
• Link prediction
• etc

3. Translating Embedding for Modeling Multi-relational Data

이제 Knowledge Graph(KG)의 node들을 embedding할 수 있는 TransE에 대해 배워보겠습니다.

Knowledge Graph

knowledge graph에서는 node를 entitie, link relation이라고 합니다. 한 KG의 relation에는 많은 종류가 있을 수 있습니다. KG에서의 link는 종류마다 갖는 의미가 다 다릅니다.

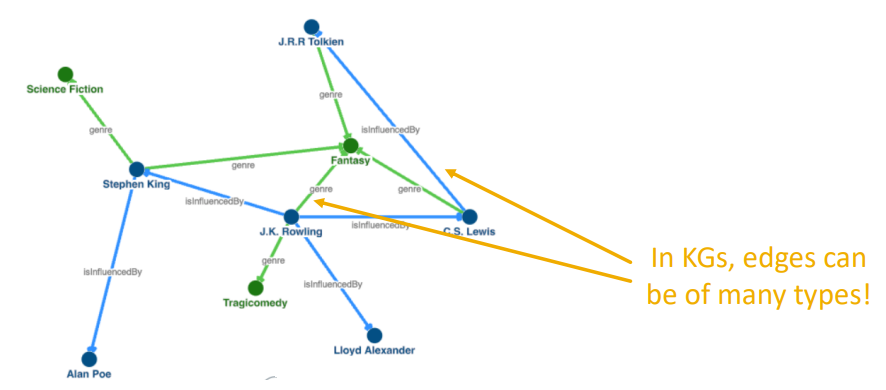
The knowledge graph represents a collection of interlinked descriptions of entities – objects, events or concepts. Knowledge graphs put data in context via linking and semantic metadata and this way provide a framework for data integration, unification, analytics and sharing.

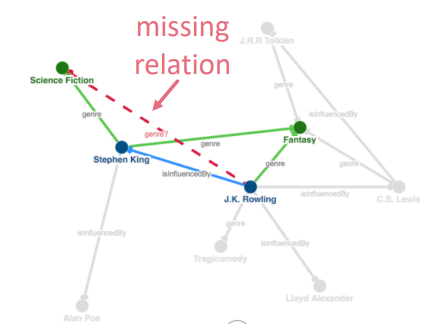
KG의 이어지지 않은 entitie(node)의 relation(link)를 예측하는 KG completion (=link prediction)에 대한 연구가 활발합니다.
intuition : KG의 local&global pattern을 잘 학습하는 link prediction model을 만들고자합니다.
downstream task : link prediction은 학습된 패턴을 사용하여 관심 node와 그 외 모든 node간의 relationship을 일반화함으로써 수행됩니다.

TransE

Abstract
지금 우리가 해결할 문제는 구성요소와 관계들을 저차원의 벡터 공간으로 임베딩 시키는 것이고, 무엇보다 지식 그래프의 기반이 되고 학습하기 쉬운 장점을 가지는 것을 목표로 한다. 이에 TransE 라는 모델을 제시하는데 이 모델은 relationship(관계)를 저차원의 임베딩된 구성요소간 translations(전환) 으로 해석한다는 것이 핵심이다.

knowledge graph를 embedding하는 TransE에서는 KG의 두 node(entity)의 관계를 triplet으로 표현합니다.
h (head entity), l (relation), t (tail entity) → (h,l,t)

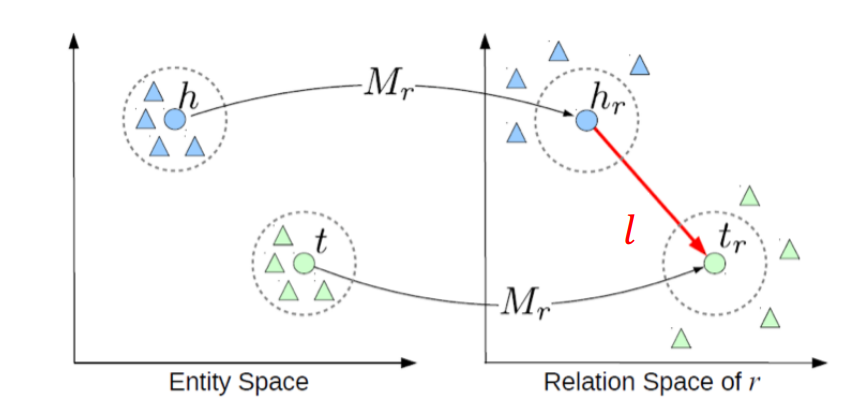
먼저 Entitie(node)들을 entitiy space $R^k$에 embedding하고, 각 Entitie $e$을 mapping function $M_r$을 통해 relation space로 mapping합니다.
TransE model을 통해 KG의 relation이 embedding space상에서 의미를 갖도록 합니다.
이때 핵심은 $(h,l,t)$가 성립한다면, $h + l\approx t$가 성립한다는 점입니다.
즉 embedding된 tail entity $t$는 임베딩 된 head entity $h$와 realtionship 과 관련된 벡터 $l$과의 합과 가까이 위치한다는 의미입니다.

• $h,t \in E$(set of entities), $l \in L$(set of relationships)
• 임베딩 벡터의 차원 : $\mathbb{R}^k$(k : hyperparameter)
• energy of triplet : $d(h+l,t)$ ($d$:dissimilarity measure,주로 $L_1,L_2-norm$
• marginary hyperparameter : $\gamma$
  $\mathcal{L}=\sum_{(h,l,t) \in S}\sum_{(h',l,t') \in S'_{(h,l,t)}} [\gamma _ d(h+l,t)-d(h'+l,t')]$
  $S'_{(h,l,t)}= \{ (h',l,t)|h'\in E \} \cup \{ (h,l,t')|t'\in E \}$

$S'_{(h,l,t)}$은 corrupted triplet입니다. 이때 corrupted는 노이즈가 추가된 상태라는 의미입니다. 위 수식에서 알 수 있듯이 head entity나 tail entity에 변화가 있는 상태입니다. $S'_{(h,l,t)}$는 실제 KG에는 없는 triplet입니다.
loss $\mathcal{L}$를 mimimize하므로, training triplet $(h,l,t)$의 energy(dissimilariy)는 작게하고 corrupted traiplet$(h',l,t')$의 energy(dissimilarity)는 크도록 학습한다는 의미입니다.
1. 먼저 Entitie(node)들을 entitiy space $R^k$에 embedding합니다.
2. 각 Entitie $e$을 mapping function $M_r$을 통해 relation space로 mapping합니다.
2. 각 Relation(link)들은

학습 과정은 다음과 같습니다.
1) relation set의 $l$에 대해 uniform distribution을 따르게 하고 정규화를 시킵니다.
2) entitiy set의 $e$에 대해 uniform distribution을 따르게 하고 정규화를 시킵니다.
3) triaining triplet set $S$에서 batch size만큼의 triplet을 뽑아 $S_{batch}$를 구성하고, $T_{batch}$를 공집합으로 초기화합니다.
4) $S_batch$에 대한 corrupted triplet을 만들어 $T_batch$에 원소로 넣어줍니다.
5) 구성된 $S_{batch}$와 $T_{batch}$로 loss를 mimize하는 방향으로 임베딩을 업데이트합니다.
6) 2)~5)를 반복합니다.

TransE는 KG에서 entities간의 관계를 잘 반영하고 기존 SE model보다 최적화가 간단합니다. 2-way interactions를 표현하는데 있어 강점이 있지만, 3-way dependencies를 표현하는데는 약점을 가집다. 또한 1-to-1 이상의 , 1-to-N, N-to-1 관계를 포함하는데 TransE는 부적합할 수 있습니다.

4. Embedding Entire Graphs

이전까지는 node를 embedding하는 방법을 배웠습니다.
이번 파트에서는 Graph $G$를 embedding하는 방법을 배워보겠습니다.
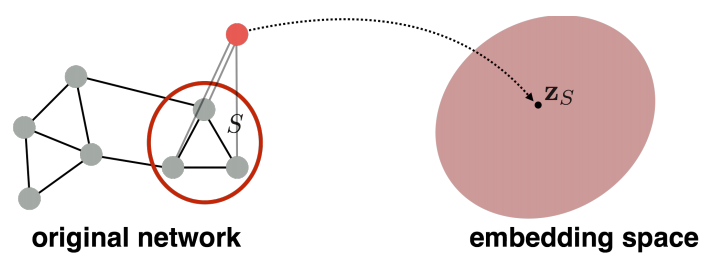
전체 graph 뿐만 아니라 전체 graph의 sub-graph를 한 point를 embedding할 수 있습니다.

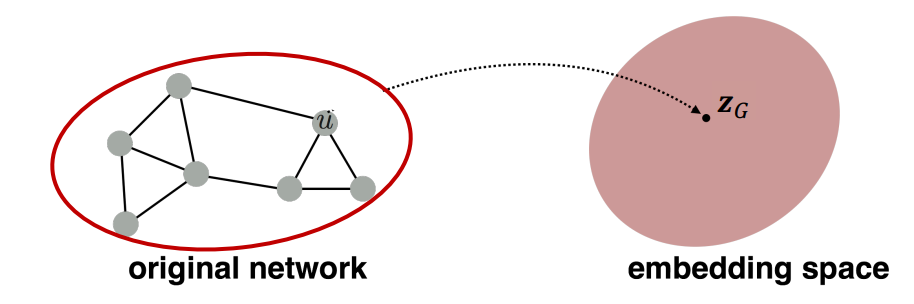
(sub)graph embedding을 통해 "Toxic molecules, non-toxic molecules 분류", "anomalous graph 분류"등을 할 수 있습니다.

다음으로 (sub)grpah를 embedding하는 몇가지 approach를 알아보겠습니다.

Approach 1
(sub)graph $G$의 각 node를 embedding하고(ex.Deep Walk, node2vec...) 그 embedding값을 모두 더하거나 평균을 내어 graph embedding을 할 수 있습니다.
sum : $z_g= \sum_{v \in G}z_v$
avg : $z_g= {{1}\over{\# \; of\; node}}\sum_{v \in G}z_v$

Approach 2
(sub)graph를 대표하는 virtual node (super-node)를 만들고, 그 node를 embedding값을 (sub)graph의 embedding으로 사용할 수 있습니다.

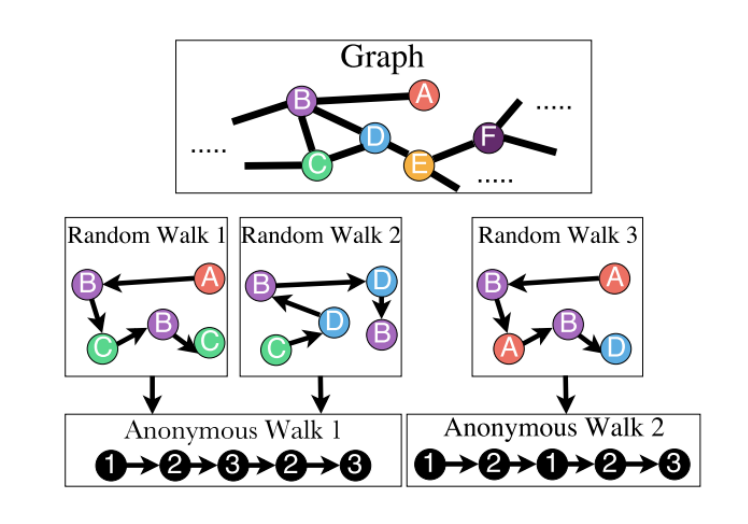
Approach 3 : Anonymous Walks Embeddings

Anonymous Walk는 random walk를 하는데 어느 node를 지나왔느냐가 아닌, 지나온 순서를 고려하는 random walk입니다. random walk를 진행하고 그 발자취의 순서(index)를 Anonymous Walk라고 합니다.
Anonymous Walk의 결과로 embedding하는 것을 Anonymous Walks Embeddings이라고 합니다.

Reference

• CS244W fall 2019 : Machine Learning with Graphs의 7강 "Graph Representation Learning"
• 데이터 괴짜님 CS224W - 07.Graph Representation Learning
• frhyme님 node2vec은 무엇인가?
• Sukwon Tun님 [지식그래프] (TransE) Translating Embeddings for Modeling Multi-relational Data