Contents

0. Intro : ML/DL on Graph
1. Node Embedding
2. Random Walk
3. node2vec
4. TransE
5. Graph Embedding

Keyword : Node Embedding , Random Walk , node2vec , TransE

0. Intro : ML/DL on Graph

Machine Learning on Graph

지난 6강에서는 graph 에 Machine Learning 을 적용하는 방법을 배웠다!
graph에 ML을 적용하면, (지난 시간에 배운) unknown label을 부여하는 node classification 이나 missing 된 edge를 예측하는 link prediction 등을 수행할 수 있다

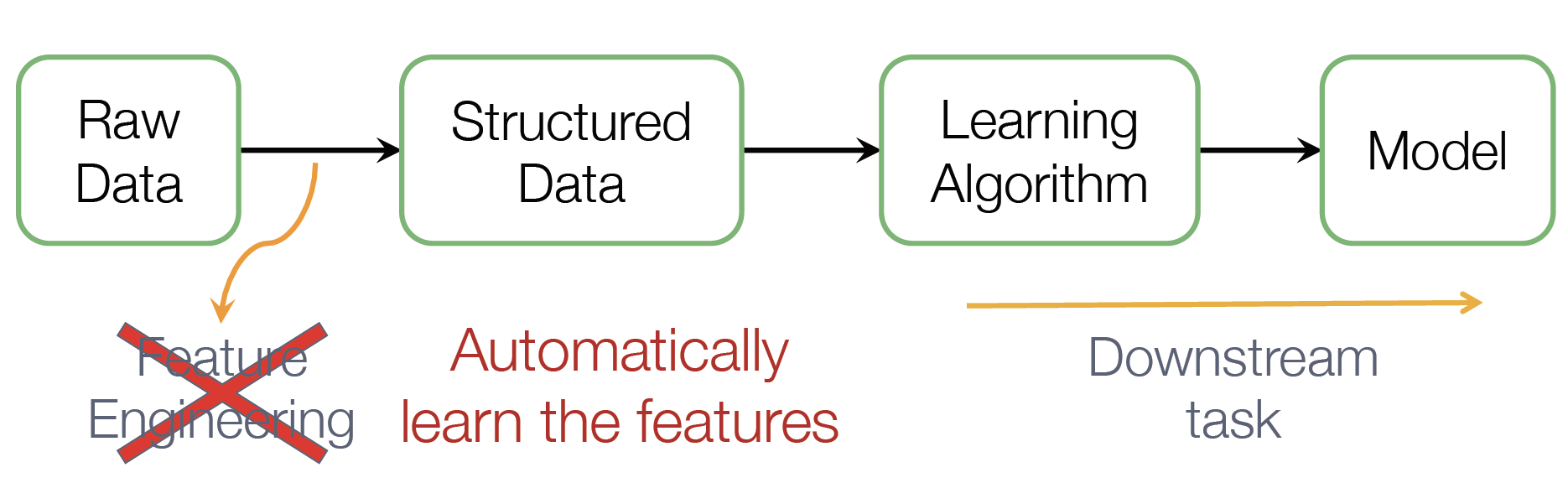
근데 머신러닝을 적용하려면 매 순간마다 Feature Engineering을 수행해야 하는데, 이게 쉽지 않다 ㅠㅠ
그래서 우리는 (힘든) FE 없이도 Automatically Learn Features 하고 싶고, 이를 통해 Downstream Task를 수행하고 싶다 ~

Feature Representation

goal : Efficient task-independent feature learning for machine learning with graphs!
= task마다 FE를 진행하기 보다는, task에 구애받지 않는 efficient 한 방법론을 찾고 싶다

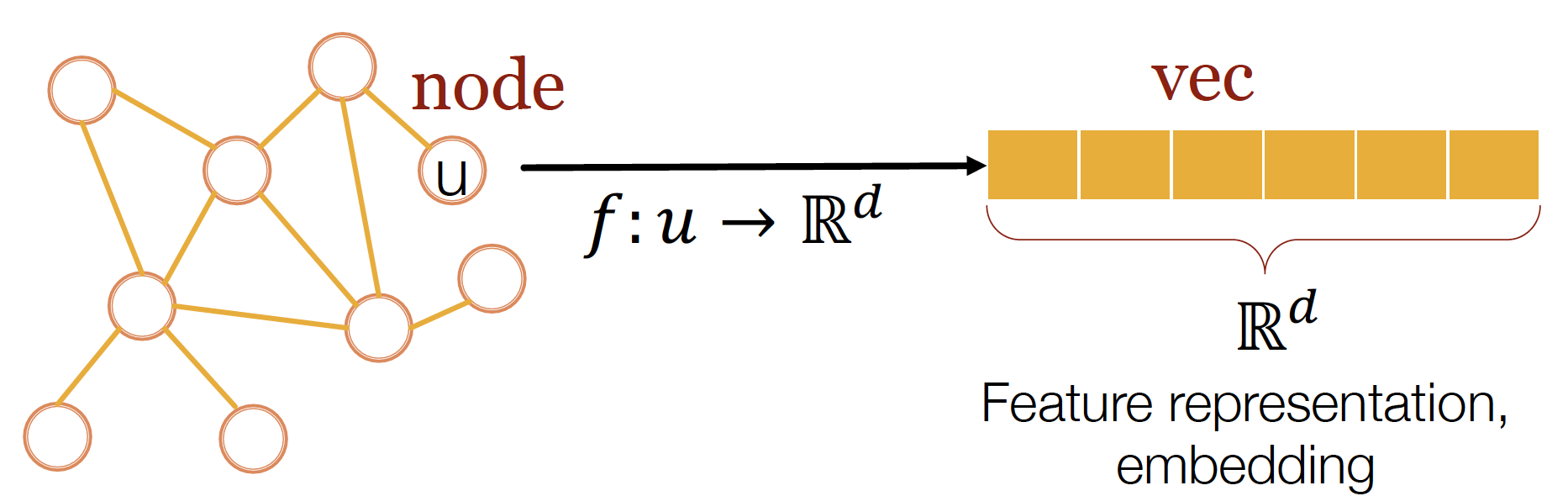
그래서 생각한 방법이 node embedding !!
node를 embedding function을 통해 latent dimension에 mapping 하여, Feature Representation 을 나타낸다 ~

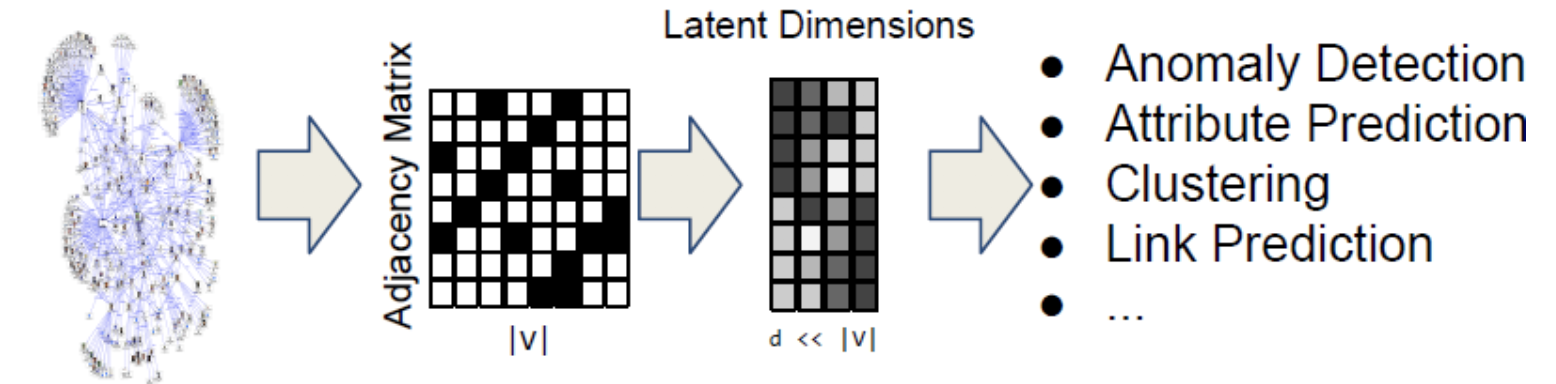
network의 각 node를 low-dimensional space에 mapping 한다
= Encode Network Information and Generate Node Representation

node의 embedding이 비슷하면, 해당 node는 network similarity 가 존재한다 ~
즉, latent space 에서의 node similarity = graph 에서의 node similarity

Deep Learning on Graph

graph domain을 deep learning 에 적용하는 것은 왜 힘든가 ...

CNN은 주변 정보를 반영해 계산하는 conv 연산을 수행하기 때문에 fixed-size image/grid에 적합하고, RNN은 이전 정보를 계속 넘겨주는 recurrent 연산을 수행하기 때문에 text/sequence에 적합하다

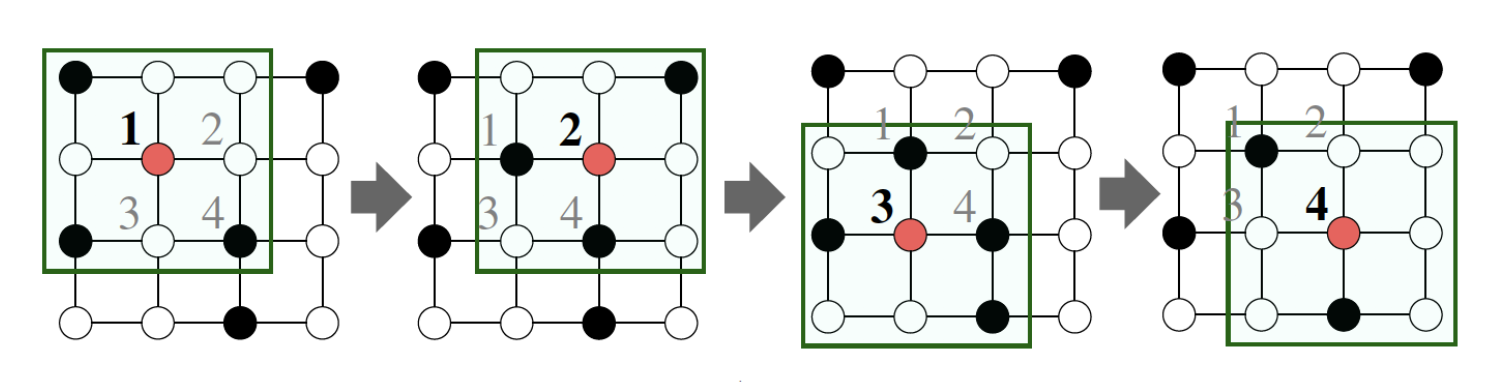
1. Network는 이보다 훨씬 topological 하게 복잡하고,
   (= 위의 그림 : missing node에 conv 연산 수행, 실제 네트워크에서는 이렇게 표현할 수 없어 cnn처럼 filter를 이동시키며 학습할 수 없다)
2. 고정된 순서나 기준점이 없으며,
3. dynamic 하며, Multimodal features (= 다양한 형태로 이루어진 데이터, ex. video QA = 이미지 & 텍스트) 를 갖는 경우도 있다

따라서 단순하게 딥러닝을 적용하기에는 무리가 있음 ~

1. Node Embedding

graph $G$ 에서,
1. $V$ : vertex set (node 집합)
2. $A$ : adjacency matrix (인접행렬)
3. node feature 및 extra informaion 이용하지 않는다!!

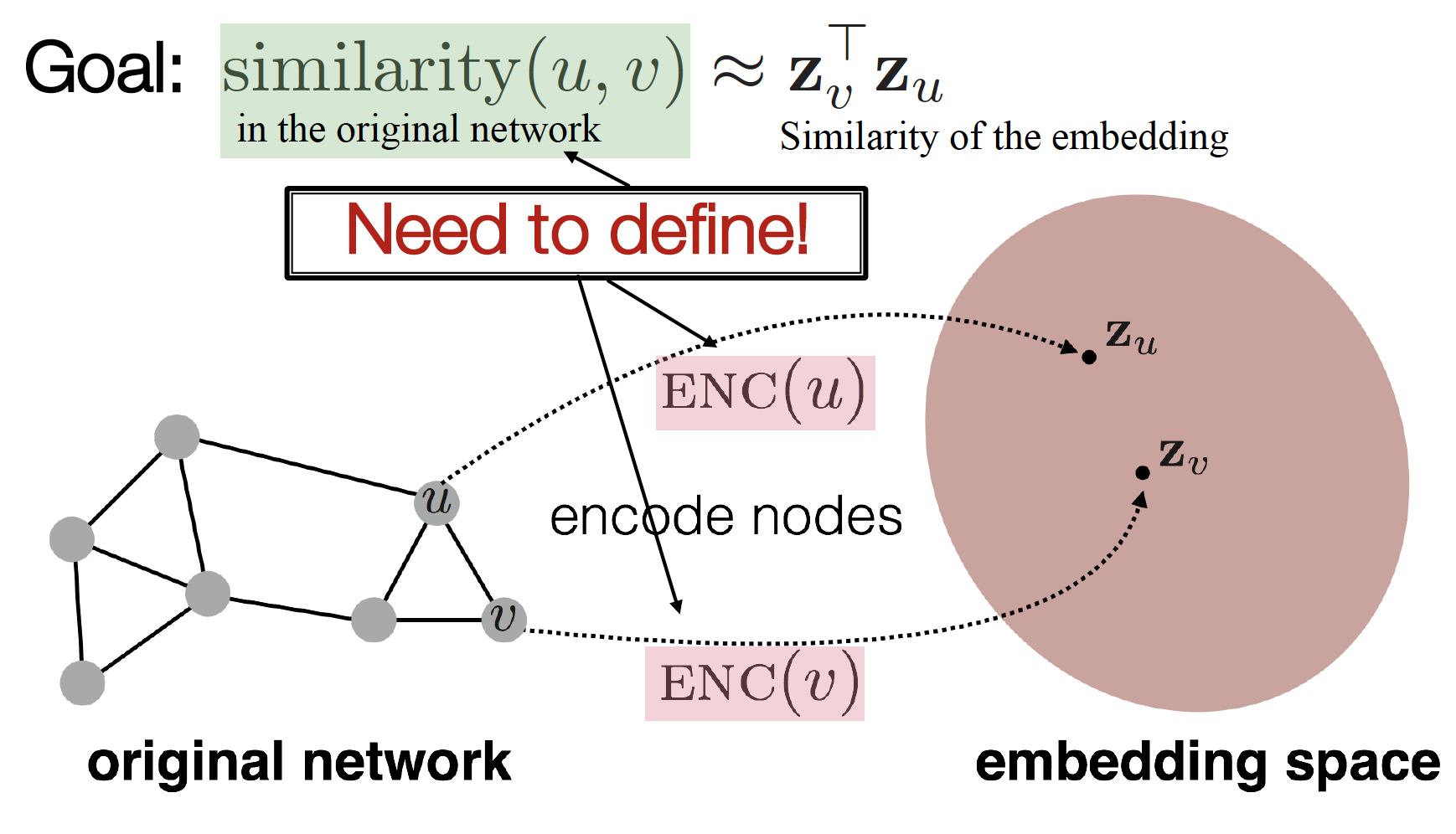
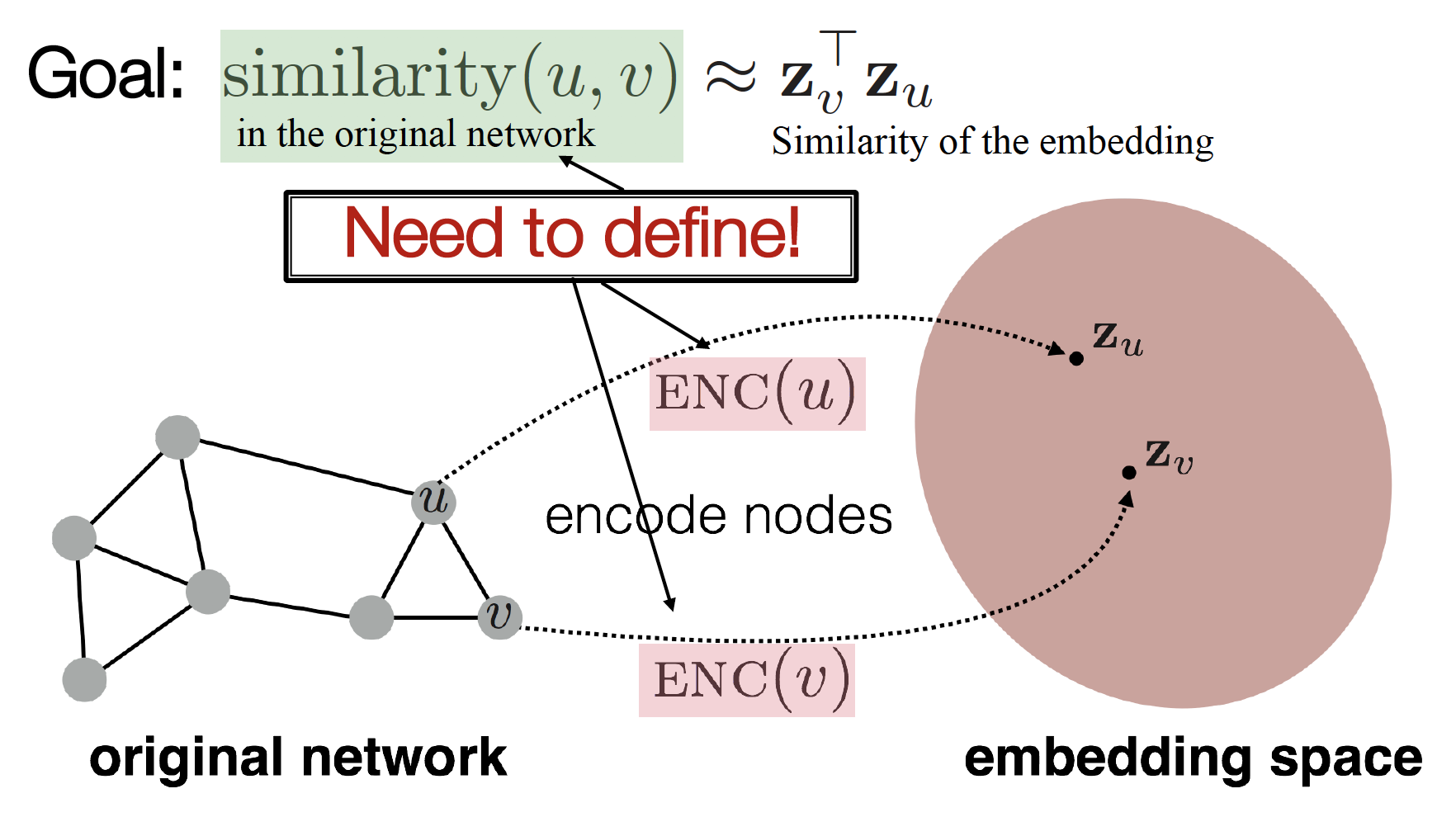
embedding node ($z_u$, $z_v$) 사이의 관계가 original network node ($u$, $v$) 사이의 관계를 가장 잘 표현해 주는 encoder ($ENC(\cdot)$) 찾기!

(= to encode nodes so that similarity in the embedding space approximates similarity in the original network)

Learning Node Embeddings

1. Define an encoder (i.e., a mapping from nodes to embeddings)
2. Define a node similarity function (i.e., a measure of similarity in the original network)
3. Optimize the parameters of the encoder so that:
   $similarity(u,v) \approx {z_v}^T z_u$

Shallow Encoding

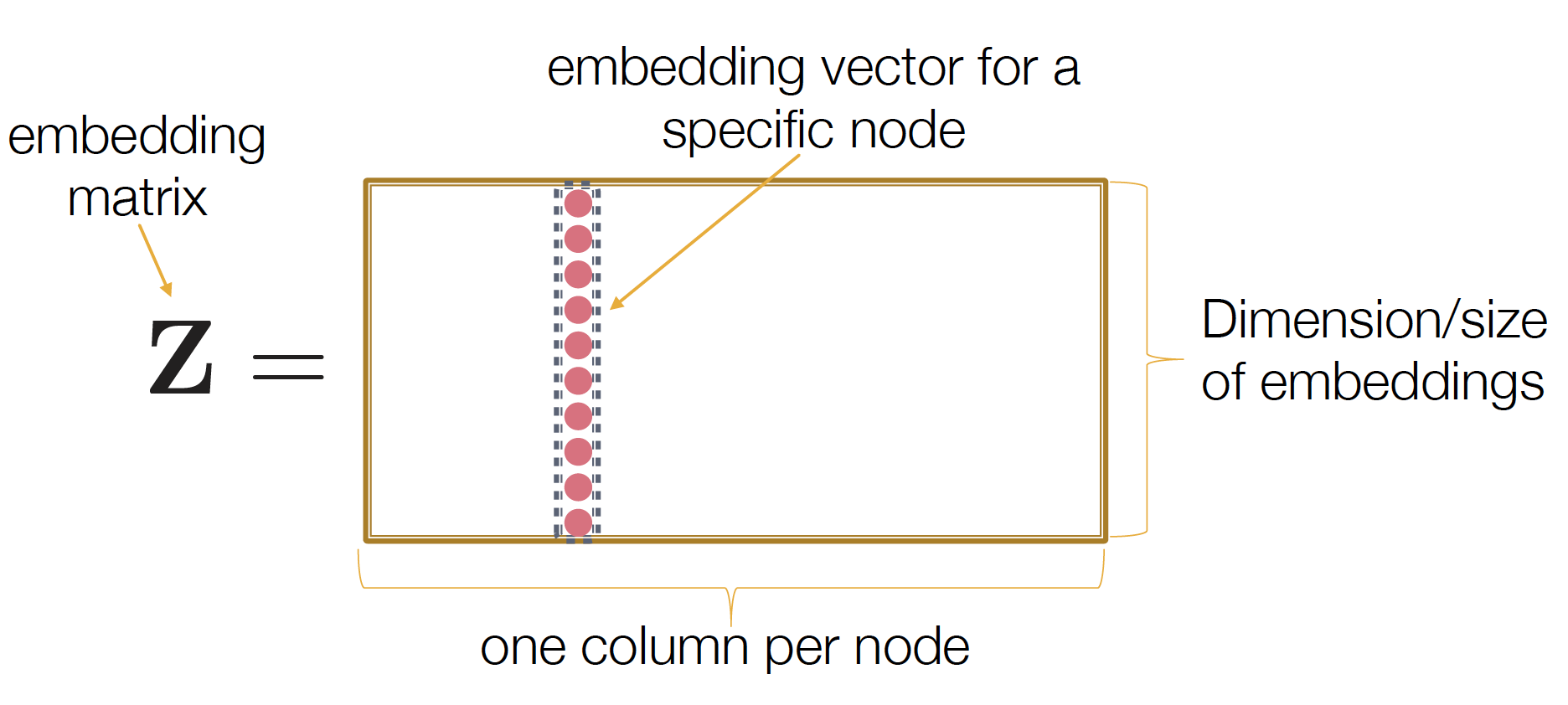
단순하게 lookup-table 을 통해 embedding matrix 만드는 방법!
lookup-table 은 여기에 잘 설명되어 있다 ~

랜덤 value로 구성된 node * dimension matrix 를 만들고, node i의 embedding 값이 i번째 column 값이 된다 ~
$similarity(u,v) \approx z_v^T z_u$ 를 optimize 하는 방향으로 $Z$ 를 학습시킨다!

lookup-table 의 경우 각 node는 unique embedding vector 를 가진다는 장점이 있지만, 랜덤하게 넣은 숫자이기 때문에 node들 사이의 관계는 전~혀 표현되지 않는다

따라서 우리는,
node들이 연결되어 있는지, neighbor를 공유하고 있는지, network에서 비슷한 structural role을 수행하고 있는지 등등 이런 정보를 embedding 할 때 더욱 정확하게 반영하고 싶고, 이런 걸 알 수 있는 node similarity 를 표현하는 encoder를 찾고 싶은 것!

그래서 다음에 나오는 방법론들이 소개 됨 ~

2. Random Walk

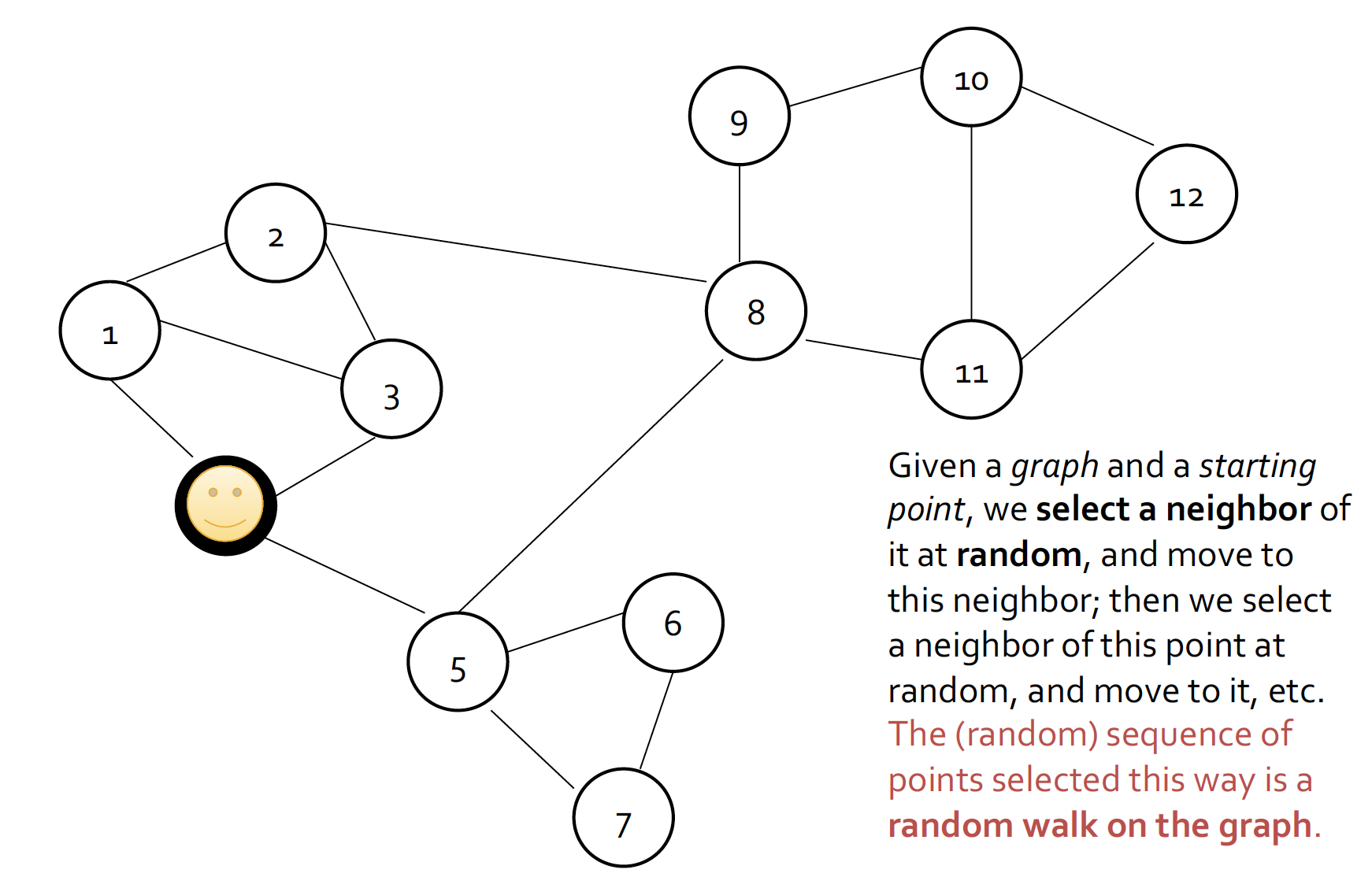
1. 랜덤으로 starting point를 잡아서 시작!
2. 해당 node의 neighbor 탐색, 랜덤으로 neighbor 설정하면서 이동

즉, random sequence 설정해서 이동한다 ~
ex. 4걸음 간다 = {[1,2,3,8], [5,8,11,12], ...}

(참고) 생각나서 적어 본 시계열에서의 Random Walk.. ($I(1)$)
$y_t = y_{t-1} + a_t$, $t=2,...,n$, $a_t \underset{i.i.d}{\sim} N(0,1)$
시간을 고려한 식을 세워서, graph의 random walk 처럼, 임의의 초기값에서 시작해서 이전값을 기반으로 계속 값을 update ~ 여러 구간에서 mean 이 일정하지 않기 때문에 비정상계열!

Random Walk Embeddings

${z_v}^T z_u \approx$ network에서 node u와 node v가 random walk에서 동시에 등장할 확률

1. starting node u에서, random walk strategy R로 이동할 때 node v 에 도착할 확률을 추정한다
   

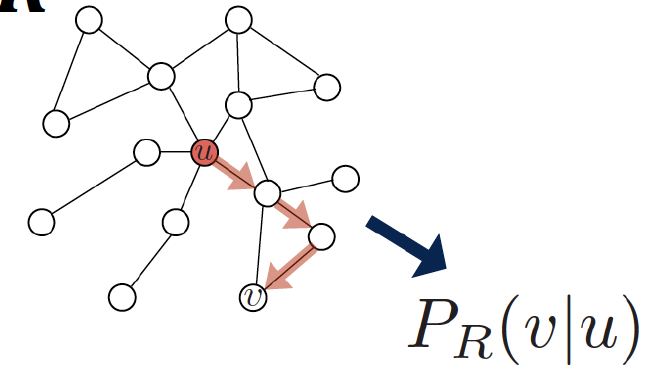
2. node u, node v 사이의 similarity 를 잘 나타낼 수 있는 embedding 방법론 (encode function)을 최적화한다
   

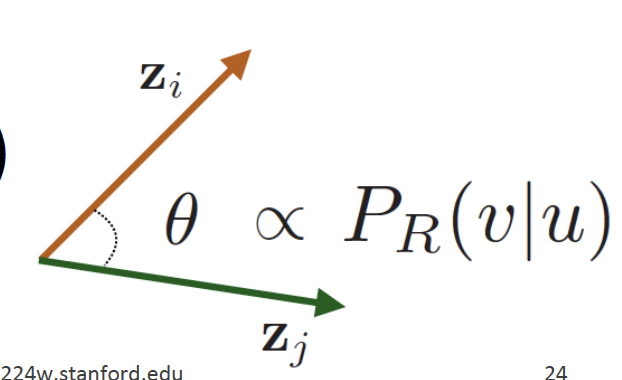
Why Random Walk?

1. Expressivity : local (본인 node 정보) & high-order neighborhood 정보 (멀리 떨어져 있는 neighborhood 정보) 모두 유연하게 고려할 수 있다
2. Efficiency : 모든 node pair를 고려할 필요 없고, random walk에서 동시 등장하는 node pair만 고려하기 때문에 효율적이다

Random Walk Optimization

graph가 주어졌을 때, 효과적으로 graph를 mapping 하는 함수 z를 찾고싶다!

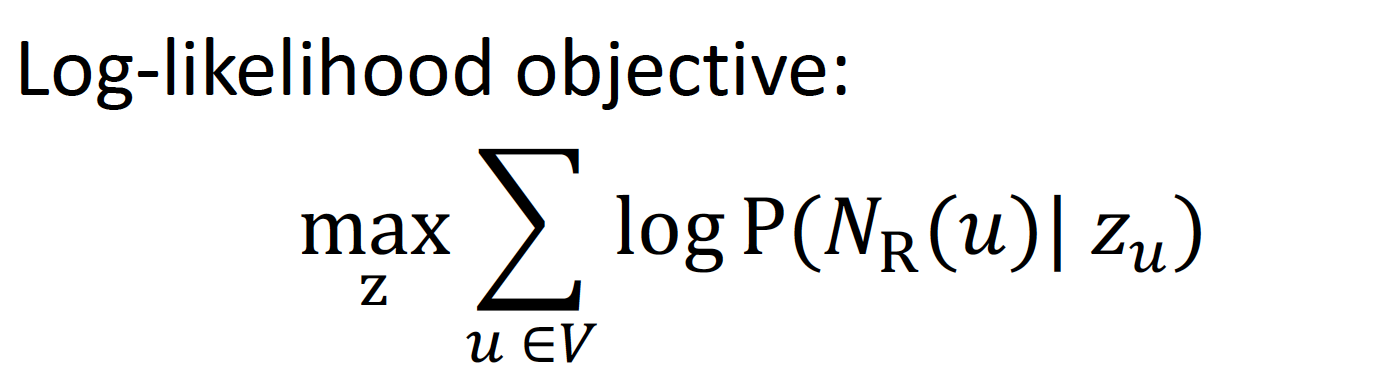
log-likelihood 목적함수를 통해 최적화한다 ~

• $N_R(u)$ : random walk strategy $R$ 로 부터 얻을 수 있는 node $u$ 의 neighborhood
• $z_u$ : vector representation

즉, node u가 주어졌을 때, $N_R(u)$을 가장 잘 예측할 수 있는 feature representation을 찾고 싶고, feature representation을 표현하는 함수(ENC)를 찾아가는 과정을 log-likelihood 값을 통해 찾아간다 ~

PROCESS

1. Graph 의 각 node 에서 정해진 짧은 길이 만큼의 random walk 수행한다 (using Strategy $R$)
2. 각 node 의 neighborhood $N_R(u)$를 수집한다
3. node $u$ 가 주어졌을 때, 해당 node 의 $N_R(u)$ 를 잘 예측하는 방향으로 node embedding 한다
   $max_z \sum_{u \in V} log P(N_R(u)|z_u)$

• loss function : node $u$ 를 embedding 한 것의 neighborhood 를 잘 예측하도록 학습!
• $P(N_R(u)|z_u)$ : (분모) 하나의 node 고정한 후, 이웃 전체 탐색 / (분자) node $u$ 와의 neighborhood

위의 식을 정리하면,

Graph 의 모든 node 에 대해, 각 node 의 neighborhood 가 random walk 시에 동시에 발견될 확률이 높아지도록 embedding 학습!
Loss 최소화 하는 방향으로 계속 업데이트 ~

Negative Sampling

근데 위의 식으로 Loss 계산하면 시간복잡도 $O({|V|}^2)$ ... 쏘머치
($\sum_{u \in V} exp(z_u^T z_v)$ 에서 하나하나 다 계산해야 하기 때문에 computation prob 발생)
그래서 Negative Sampling 이용한다 ~

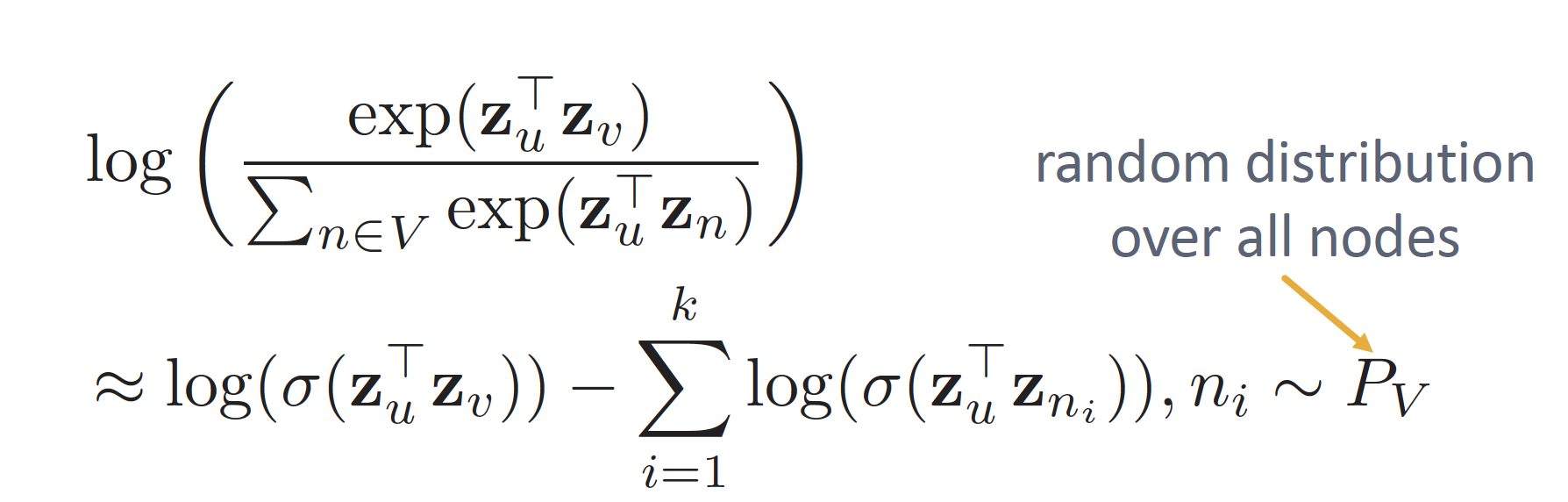
NLP에서의 negative sampling 은, ($\approx$ 오른쪽 식에서)
왼쪽 log 항에 해당되는 값이 맞는 pair, 오른쪽 sigma에 해당하는 값이 틀린 pair (이 안에 원래 - 값 들어감!)
즉, context window에서 맞는 값 끼리 계산하고, noise pairs에서 일부러 sampling 을 진행해서 word2vec의 효율성을 높이는 방법론 인디...

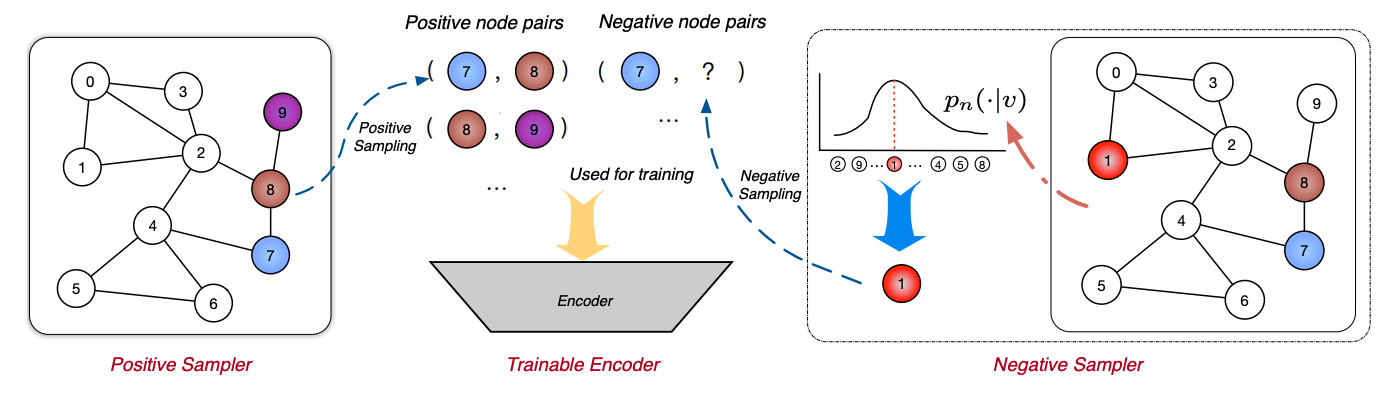
graph 에서는,
맞는 pair에서 probability 계산하고, k개의 negative node를 뽑을때는 network 전체에서 sampling 해서 뽑는다!
하나씩 다 따져가면서 (얘가 내 진짜 neighbor 인지 아닌지 따져서 아닌 애들만 뽑으면) 너무 비용 많아지기 때문에 random으로 하는게 good good 이라구 함..

negative sample 의 개수 $k$ 의 의미

• higher $k$ gives more robust estimates
• higher $k$ correspond to higher bias on negative events

실제 $k$ 는 5~20 으로 설정한다

Challenges

만약 두 node 의 structural role 이 비슷하지만 멀리 떨어져 있는 경우에, random walk 는 fixed size 조건으로 neighborhood node 를 탐색하기 때문에, 이와 같은 특성을 반영하지 못한다 ~
따라서 graph structure 정보를 활용하기 위해, node2vec 을 고려한다 ~

3. node2vec

abstract : we learn a mapping of a nodes to a low-dimensional space of features that maximizes the likelihood of preserving network neighborhoods of nodes

graph 에서 특정 node 에 대해, 그 node 의 neighborhood 가 나타날 확률을 최대화!

idea : use flexible, biased random walks that can trade off between local and global views of the network

위의 Random Walk 방법론 (=DeepWalk)은 현재 위치만 고려하므로 unbiased 하게 계산하는데, node2vec은 약간의 bias 허용! 2nd order 의 random walk 까지 고려한다 ~

node의 이웃까지 고려해서 random walk 진행한다는 의미인 듯..

1st-order vs 2nd-order random walk

• 1st-order random walk : node to node transition
• 2nd-order random walk : edge to edge transition

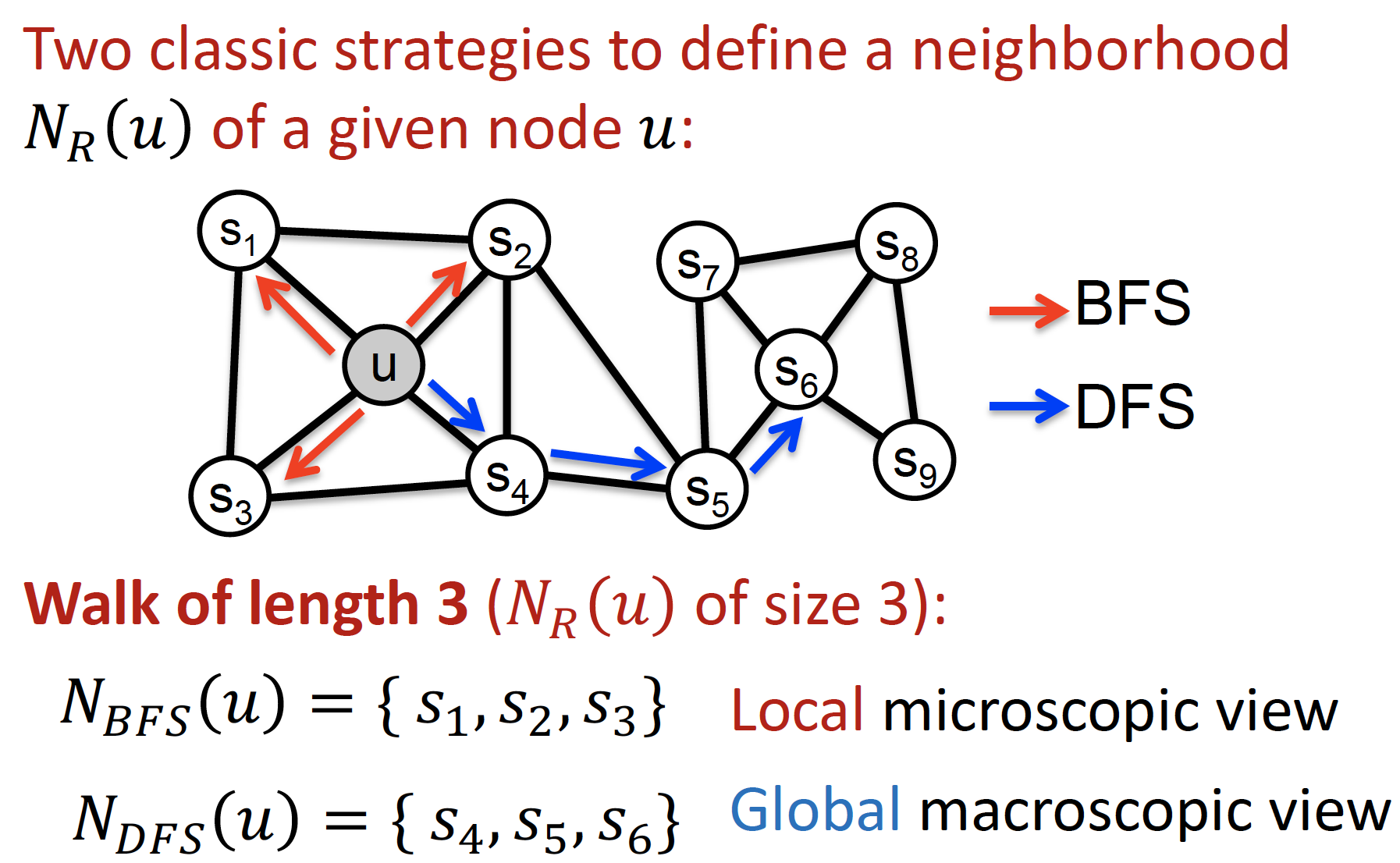
BFS, DFS 둘 다 고려해서 neighborhood 고려!

• BFS : 너비 우선 탐색, 바로 인접해 있는 노드들 넓게 탐색
• DFS : 깊이 우선 탐색, 인접 노드 중 하나 깊게 깊게 탐색

parameters

• p : Return parameter, previous node로 돌아갈 가능성을 계산
  주변을 잘 탐색하는지!
• q : In-out parameter, BFS vs DFS 비율 정의
  얼마나 새로운 곳을 탐색하는지!

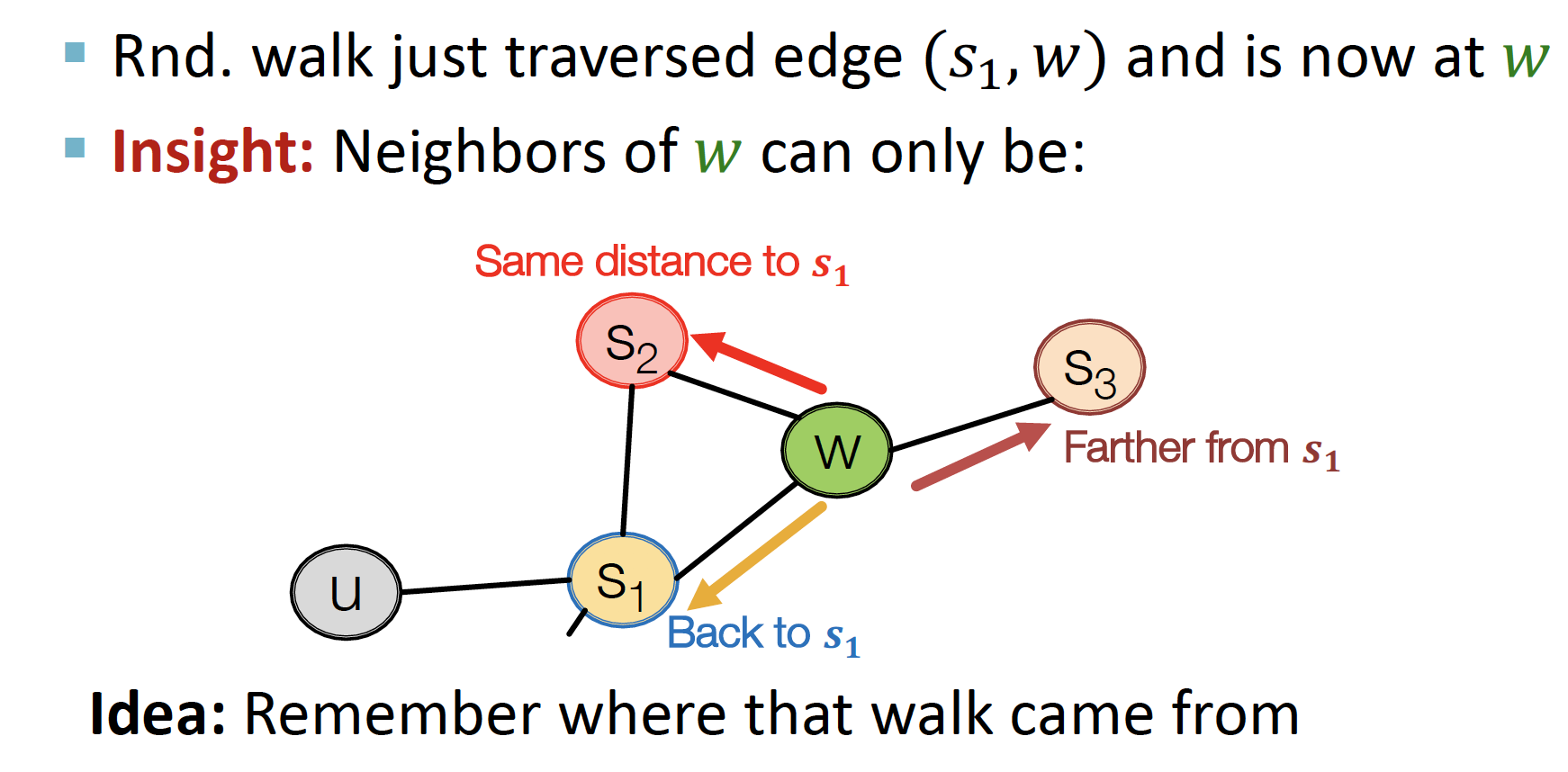
random walk는 s1 에서 w로 갔을 때, 내가 지금 w에 있다는 것만 고려하는데
biased 2nd-order random walk는 s1, s2, s3로 부터 왔다는 것을 모두 기억한다 ~

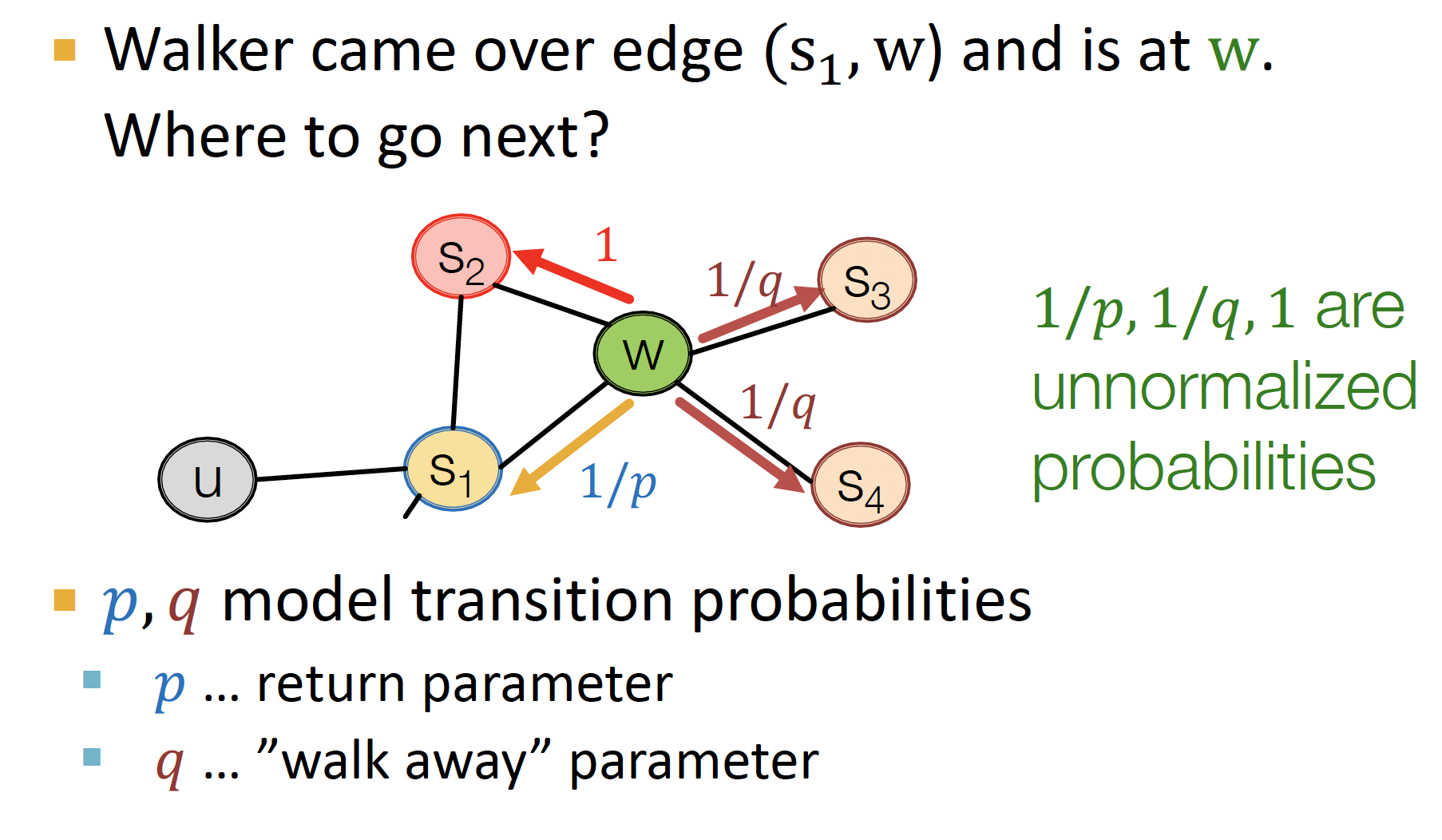
그럼 내가 현재 $s_1$ 으로부터 출발해서 w에 있을 때, 다음에 난 어디로 가야 할까 ~
p, q를 통해 결정한다!

• s1 : s1으로부터 왔으므로 1/p
• s2 : 공유하는 node 로 가는 확률, $(s_1, w)$ 에 모두 연결되어 있으므로 ~ 그래서 1
• s3, s4 : $(s_1, w)$ 중 w 하나에만 연결되어 있어서, parameter q로 결정됨

p가 작을수록 BFS-like walk (좁은 지역 고려), q가 작을수록 DFS-like walk (넓은 지역 고려)

node2vec algorithm

1. Random walk 확률 계산
2. 각 노드 u에서 출발하여 길이 l짜리 random walk를 r개 simulate
3. SGD를 이용하여 node2vec objective 최적화

4. TransE

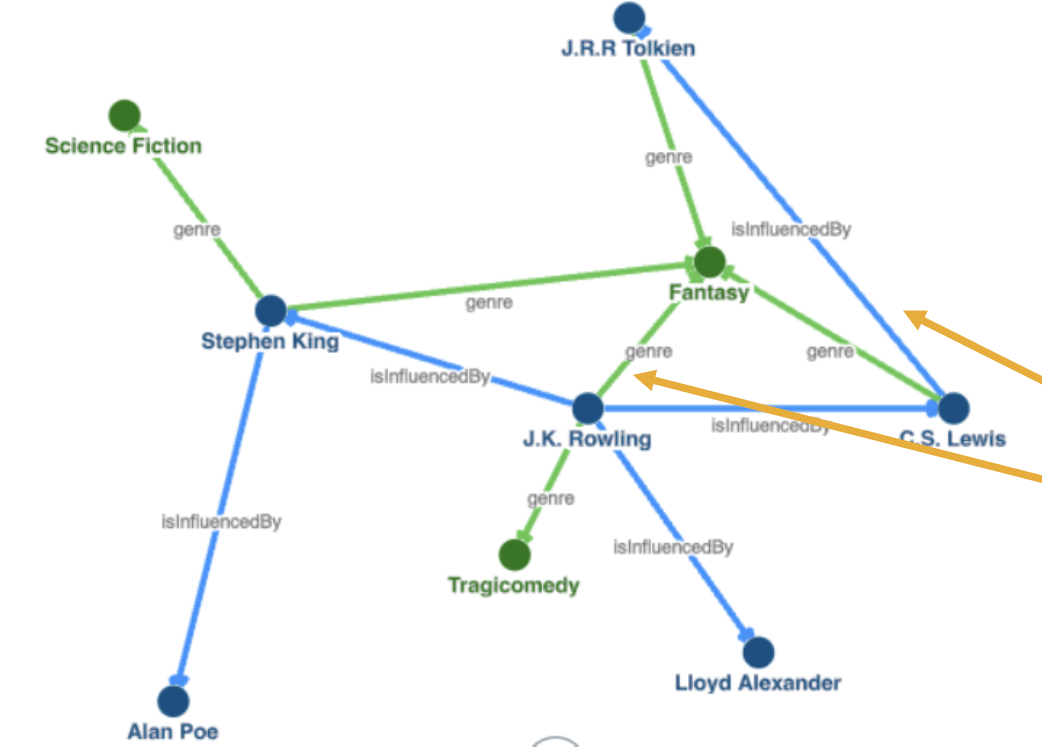
Knowledge Graph 는 위와 같이 표현된다 ~
node 는 entity 를 나타내며, edge 는 relation 을 나타낸다

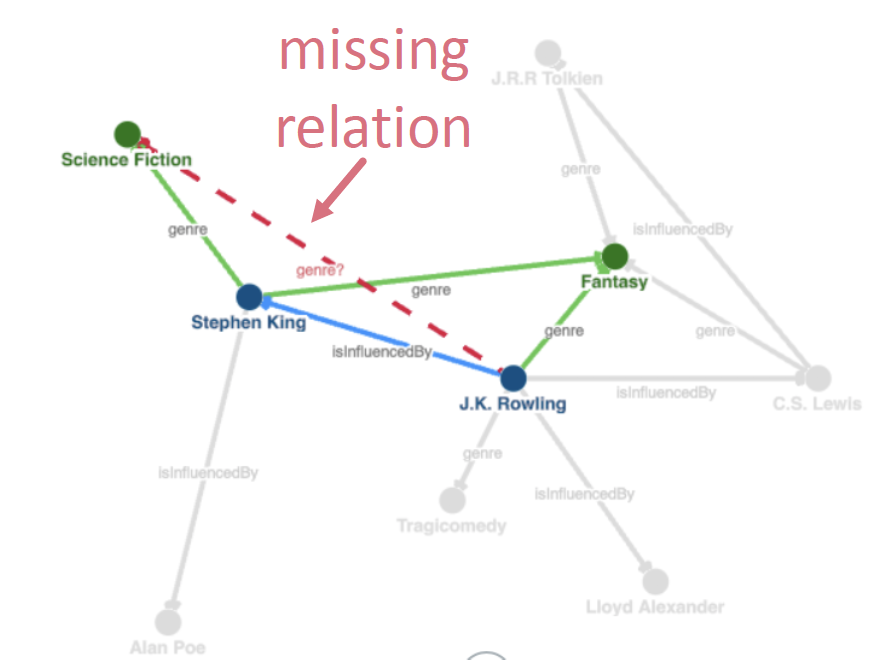
KG (=Knowledge Graph... 별다줄) 에서는 missing edge, 즉 이어지지 않은 entity (node) 의 relation (edge)를 예측하는 KG completion (=link prediction) 에 대한 연구가 활발하다고 한다 ~

따라서 KG 에 있는 local and global connectivity patterns을 학습해서, missing relation을 예측하는 link prediction model 을 만들기를 원한다 ~

Translating Embeddings

𝒉(head entity), 𝒍(relation), 𝒕(tail entity) = (𝒉, 𝒍, 𝒕)
node 와 relationship 을 triplet 형태로 표현한다!

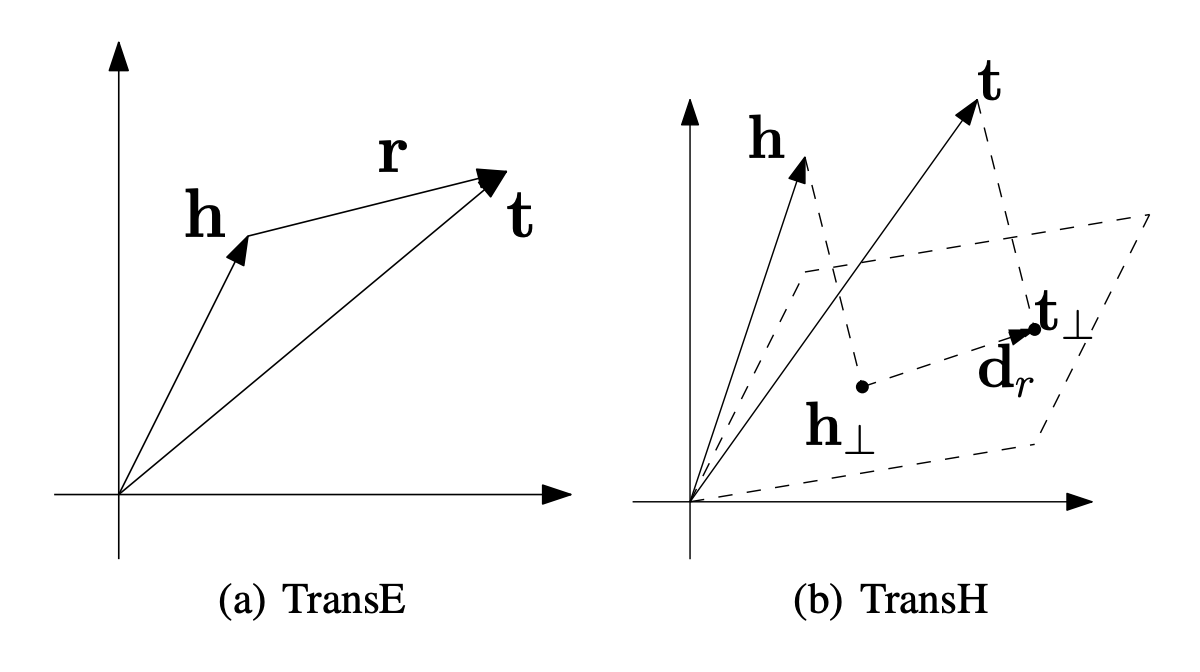
transE = Relations are represented as translations
head + relation = tail 처럼, $h + l \approx t$ 가 되게끔 하고 싶다는 것 ~
즉, KG 의 relation 이 embedding space 상에서 의미를 갖도록 한다

J.K.Rowling(h), C.S.Lewis(t) 둘 다 genre(l) 거리와 방향의 벡터만큼 이동하면 둘 다 Fantasy 라는 embedding 값이 나오게끔 하는 것이 목표 ~
이처럼 연산으로 관계를 표현할 수 있기를 기대한다 ~

transE 의 objective function 은,
$L(h,r,t) = max(0, d_{pos} - d_{neg} + margin)$
즉, train set 에 있는 positive triplet 에서, negative sampling 을 진행하여 값을 빼 준다! negative sample 은 실제 KG 에 없는, $L(h',r,t)$ (head 를 바꾼 triplet) 과 $L(h,r,t')$ (tail 을 바꾼 triplet) 으로 구성된 corrupted triplet 을 말한다 ~
Loss function 의 의미는, postive sample의 distance가 negative sample의 distance보다 최소한 margin만큼은 가까워야 한다는 것!

transE 는 1:1 relationship 을 표현하는 데에는 탁월하지만, 1:N, N:1, N:N 의 경우 부적합하다

따라서 relation을 hyperplane 에 projection 시킴으로써, 각 entity 마다 여러 relationship 을 표현할 수 있는 transH 가 등장하게 된다 (위의 위 오른쪽 그림)
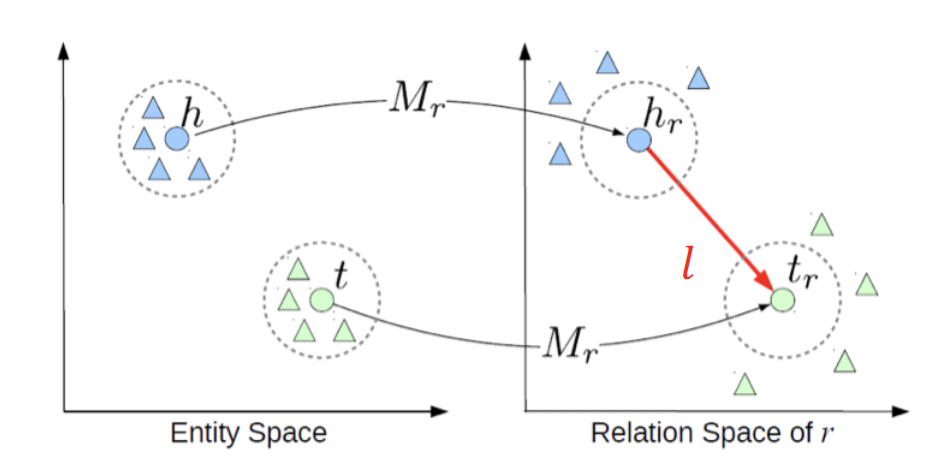
이에 더하여, entity와 relation이 동일한 semantic space 에 두지 않고, entity와 relation을 구분된 공간(entity space, multiple relation spaces)에 embedding하자는 아이디어를 적용한 transR (바로 위의 그림) 이 등장하게 된다 ~

5. Graph Embedding

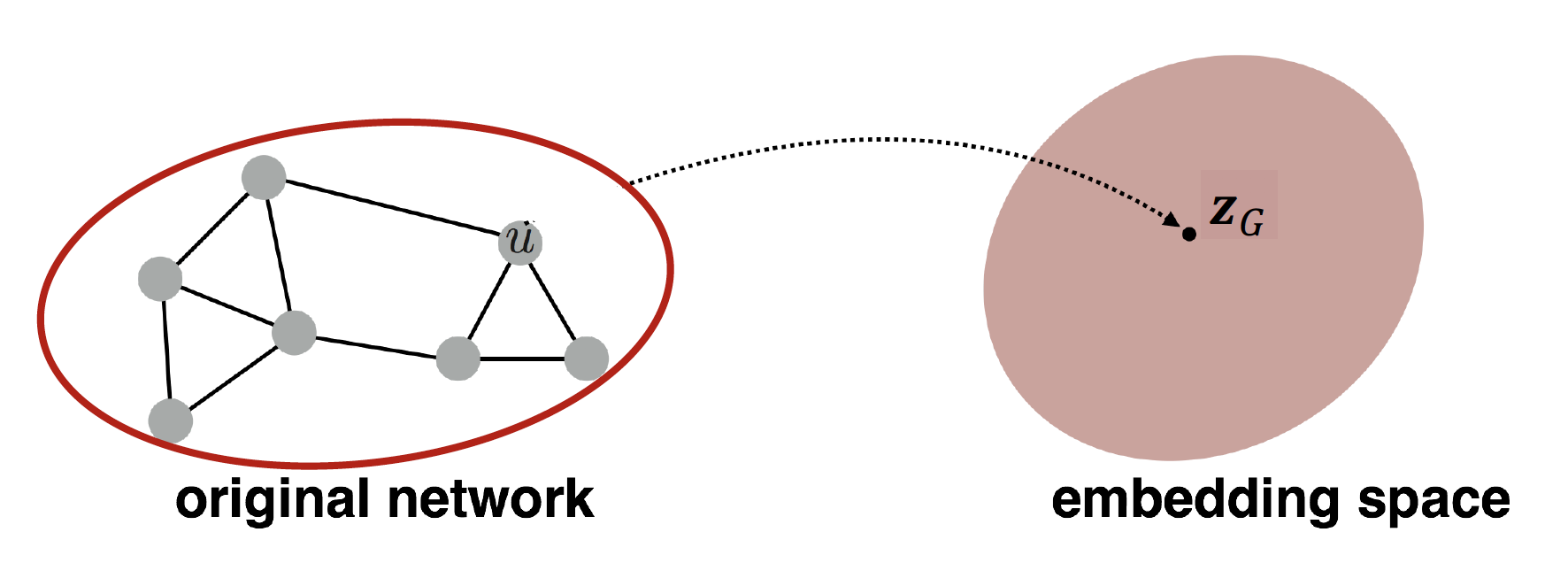
그래프 전체 (network)를 embedding 하려면 어떻게 할까 ~

Approach 1.

$z_G = \underset{v \isin G}{\Sigma} z_v$
graph 의 각 node 를 embedding 하고, node embedding 값을 다 더하거나, 평균낸다 ~

Approach 2.

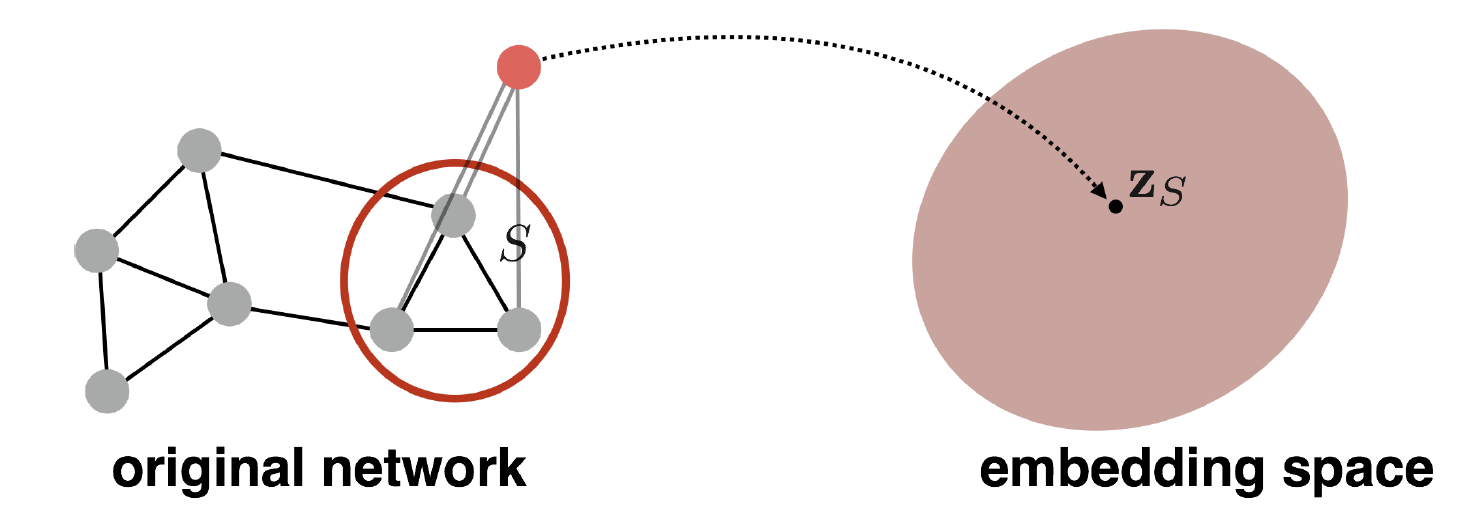
그래프를 대표하는 virtual node (=super-node) 만 embedding 하여 사용한다 ~

Approach 3. Anonymous Walk Embeddings

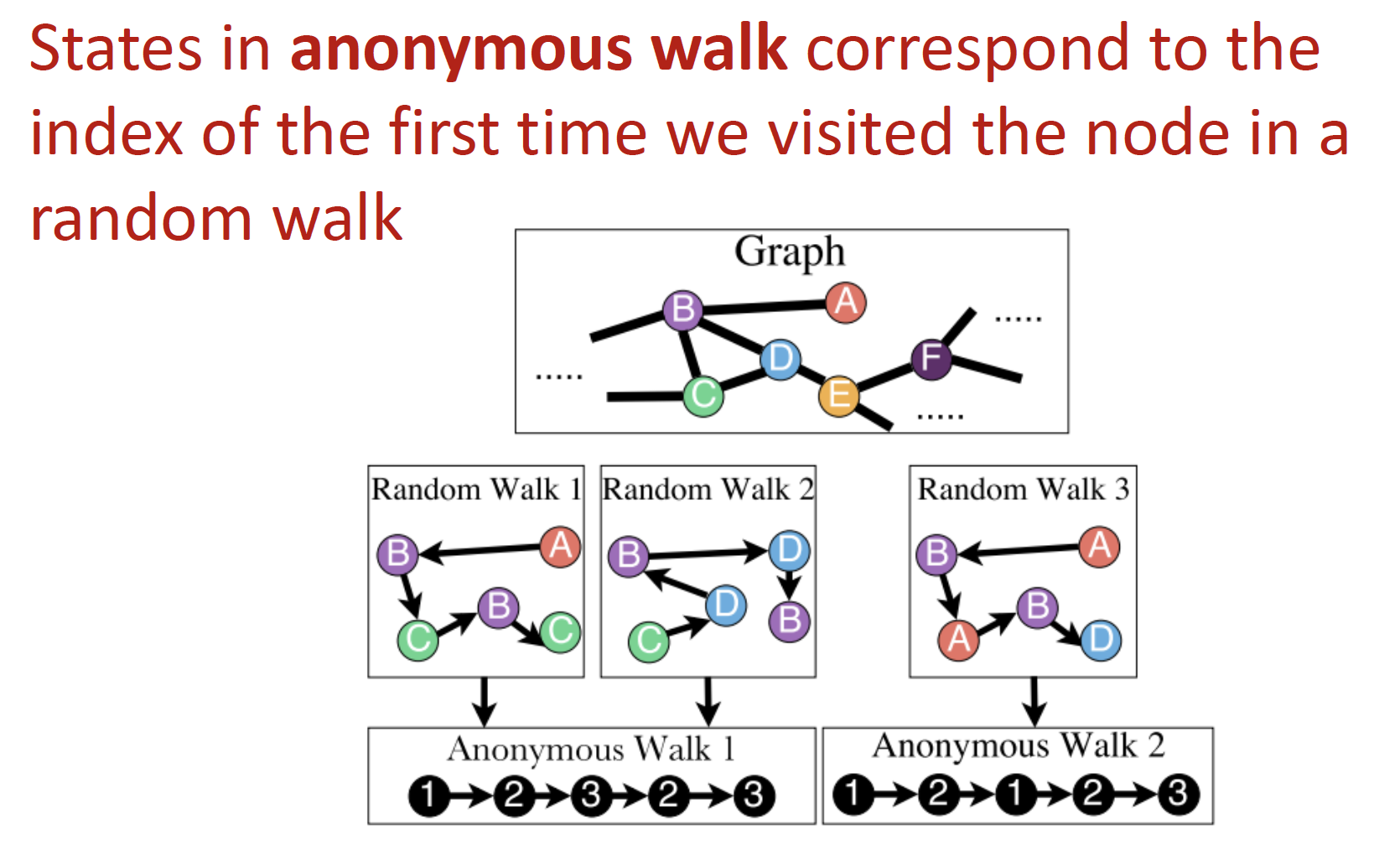
랜덤 node에서 시작해서 random walk를 진행하고, 방문한 순서대로 index를 뽑아서 이를 저장한다 ~

Reference

1. 짱짱 멋진 민정멋져 띵강 & 벨로그 리뷰
2. 12기 투빅스 그래프 스터디 윤종이 리뷰

---

3. 데이터 괴짜님 Review : CS224W - 07.Graph Representation Learning
4. lumiamitie님 Review : Graph Representation Learning (node2vec)

---

5. Understanding Negative Sampling in Graph Representation Learning
6. DeepWalk: Online Learning of Social Representations
7. node2vec: Scalable Feature Learning for Networks
8. transE : Translating Embeddings for Modeling Multi-relational Data
9. transH : Knowledge Graph Embedding by Translating on Hyperplanes
10. transR : Learning Entity and Relation Embeddings for Knowledge Graph Completion

---

11. 07. 파이토치(PyTorch)의 nn.Embedding()
12. transR Paper Review : Learning Entity and Relation Embedding for Knowledge Graph Completion