6. Message Passing and Node Classification
CS224W Review

작성자 : 이재빈
Contents
- Intro
- Relational Classification
- Iterative Classification
- Belief Propagation
Keyword : Machine Learning applied on Graph, Node Classification
0. Intro
Main Question
Network에서 몇 개의 node에만 label이 달려 있고, 몇 개는 모른다면,
모르는 node의 label을 어떻게 설정해 줄 수 있을까요?
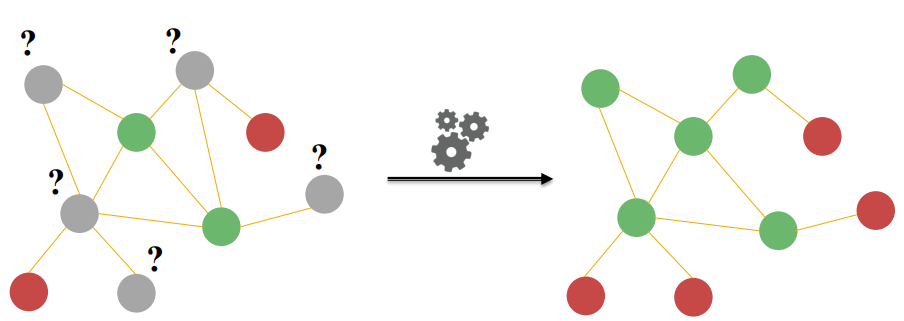
주어진 label을 이용하여, unlabeled node를 예측합니다!
이와 같은 방법론을 semi-supervised node classification 이라고 합니다.
semi-supervised learning
supervised learning
관측치마다 정답 label이 달려 있는 데이터셋을 이용하여 학습
ex. Regression, Classification, Neural Network, ...unsupervised learning
정답 label이 달려 있지 않은 데이터셋을 이용하여, 모델 스스로 학습
ex. Clusteringsemi-supervised learning
label이 달려있는 데이터와 label이 달려있지 않은 데이터를 동시에 학습해서, 더 좋은 모델을 만드는 것
데이터가 군집의 형태를 따르고 있다면, 학습에 도움이 될 것

Network를 구성하고 있는 node 끼리는 Cluster(=Community, Correlation)를 형성하고 있을 것이므로, semi-supervised learning을 통해 unlabeled node를 분류해 보자는 것이 핵심 idea 입니다.
Collective Classification
Network 상에는 Correlation이 존재합니다.
Similar node는 connected 되어 있을 것이고,
이러한 정보를 기반으로 node에 label을 assign 해 주는 것이 collective classification 개념입니다.
Collective Classification Techniques
1. Relational Classification
2. Iterative Classification
3. Belief Propagation Correlations Exist in Networks
Individual behaviors are correlated in a network environment
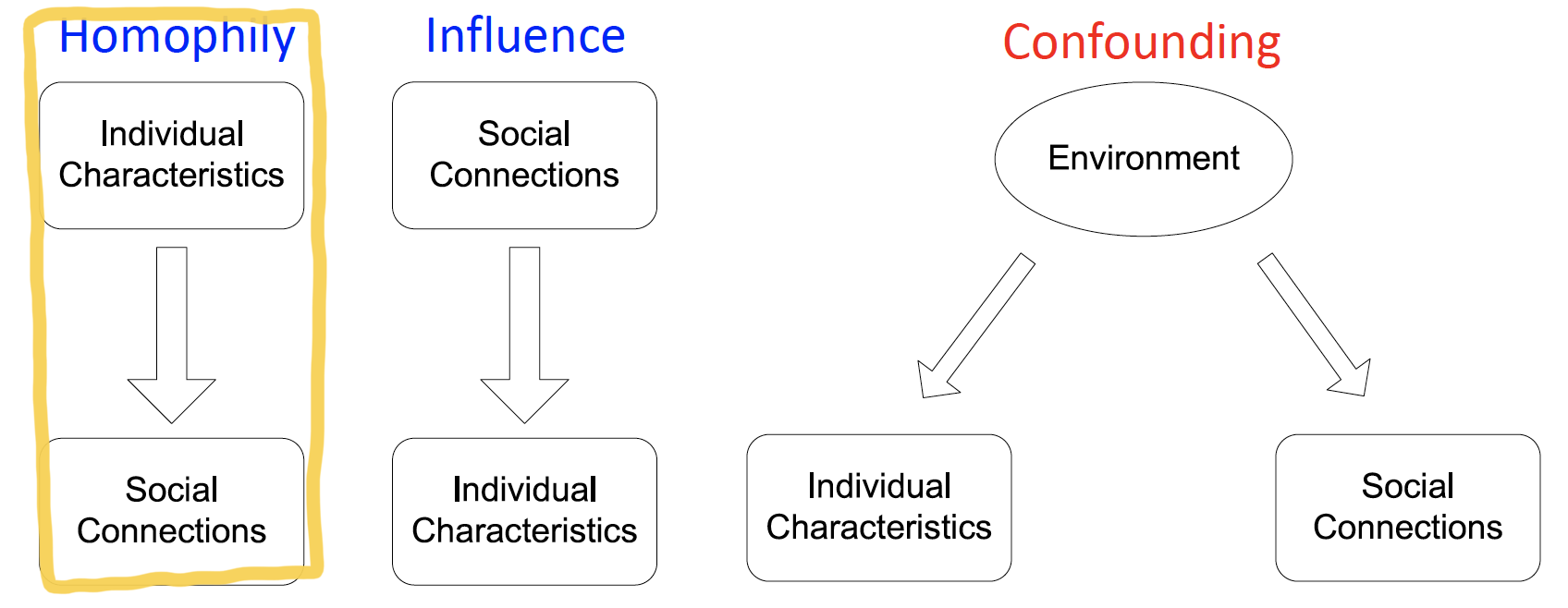
-
Homophily- 유유상종
- 비슷한 성향을 가진 사람들끼리, 비슷한 social connection을 형성
- ex. age, gender, organization roles + AI에 관심 많은 투빅스..
-
Influence- 나의 취향을 추천하여, 다른 사람도 좋아하게끔 만드는 것
- ex. 내가 좋아하는 연예인을 동료한테 매일 보여줬더니 동료도 결국 그 연예인을 좋아하게 되는 것
-
Confounding
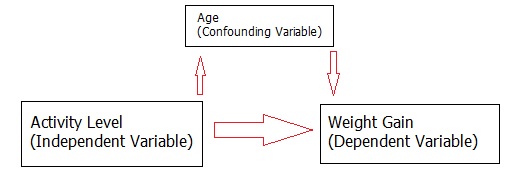
- 교란 변수 : individual characteristics와 social connections에 동시에 영향을 주는 environment

correlation 중, homophily에 주목해 node classification을 수행하고자 합니다.
Classification with Network Data
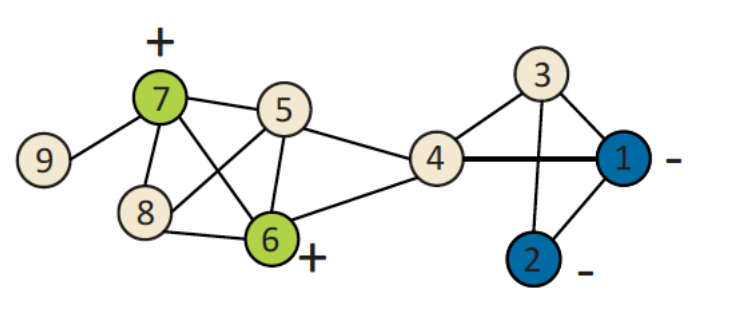
How do we leverage this correlation observed in networks to help predict node labels?
Guilt-by-association
If I am connected to a node with label 𝑋, then I am likely to have label 𝑋 as well.
= 내가 투빅스 사람들하고 친구라면, 나도 투빅스 사람일 확률이 크다!

v node label 은 위의 세 가지 요소에 영향을 받게 됩니다.

따라서 node classification task는,
positive / negative / unlabeled node 에서,
unlabeled node 가 positive node가 될 확률을 예측하는 것 입니다.
(cf. logistic regression에서의 p = 1이 될 확률)
Collective Classification Overview
Simultaneous classification of interlinked nodes using correlations
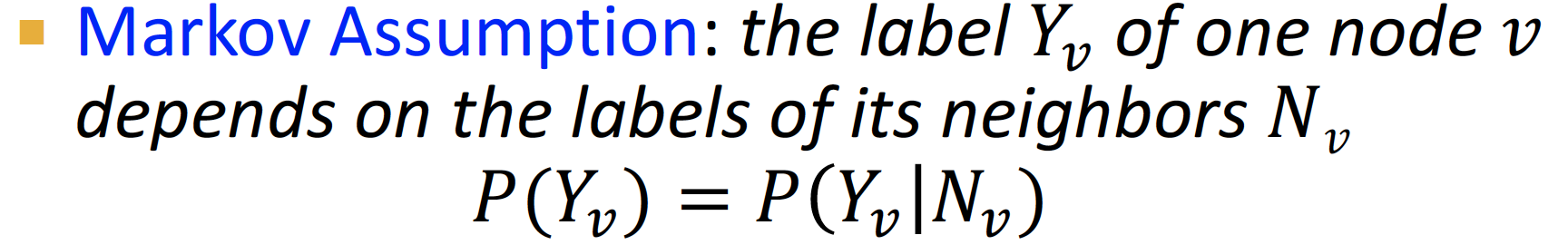
Markov Property:Markov Assumption: neighbor 에 모든 정보가 함축되어 있다고 생각하고, node v에 연결된 neighbor 정보를 고려합니다.

PROCESS
STEP 1. Local Classifier
- 초기 label을 부여합니다.
- node 속성만을 사용해 예측하며, network 정보를 사용하지 않습니다.
STEP 2. Relational Classifier
- correlation 을 capture 합니다.
- neighborhood node의 label, attribute 정보를 사용해 예측합니다.
STEP 3. Collective Inference
- Propagate the Correlation
- 각 node마다 Relational Classifier 를 반복적으로 적용합니다.
- 인접한 neighbor 정보만 사용하는 것이 아니라, neighbor에 전달된 correlation을 사용합니다. 이를 통해 전체 network의 정보를 사용할 수 있게 됩니다.
(Basically, we do not want to stop at the level of only using our neighbors, but through multiple iterations we want to be able to spread the contribution of other neighbors to each other.)
Collective Classification 은 iterative 하게 진행되며, approximate inference 입니다.
iterative: neighborhood labels 불일치가 최소화 될 때 까지 반복합니다.approximate inference: propagation 진행할 때 neighborhood 범위를 점점 줄입니다.
several applications
- Document classification
- Part of speech tagging
- Link prediction
- Optical character recognition
- Image/3D data segmentation
- Entity resolution in sensor networks
- Spam and fraud detection
1. Relational Classification
setting
idea: 의 class probability는 neighbor 노드들의 class probability의 weighted averagelabeled node: ground-truth Y label 로 initializeunlabeled node: uniformly 하게 설정합니다. (0.5 or 신뢰할 만한 prior)
training
update: 수렴할 때 까지 or 최대 iteration 수에 도달하기까지 모든 노드들을 random order로 업데이트 합니다.repeat: 모든 node i 와 label c에 대해, 다음 과정을 반복합니다.
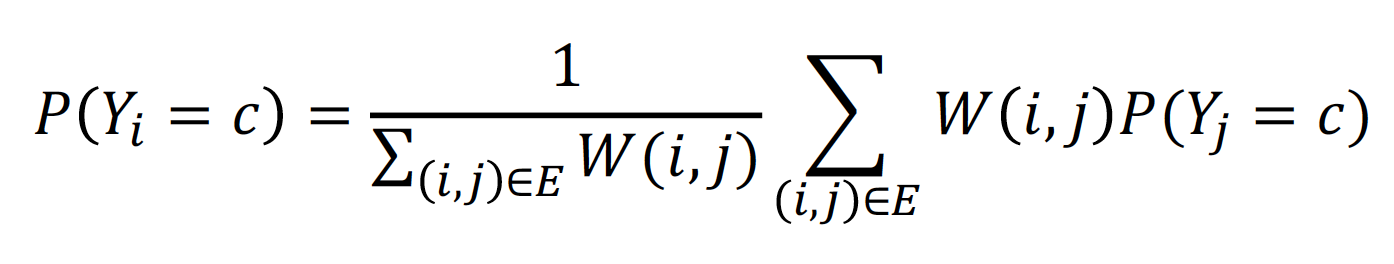
Example
Initialize: node label 에 맞게, 확률값을 초기화 합니다.
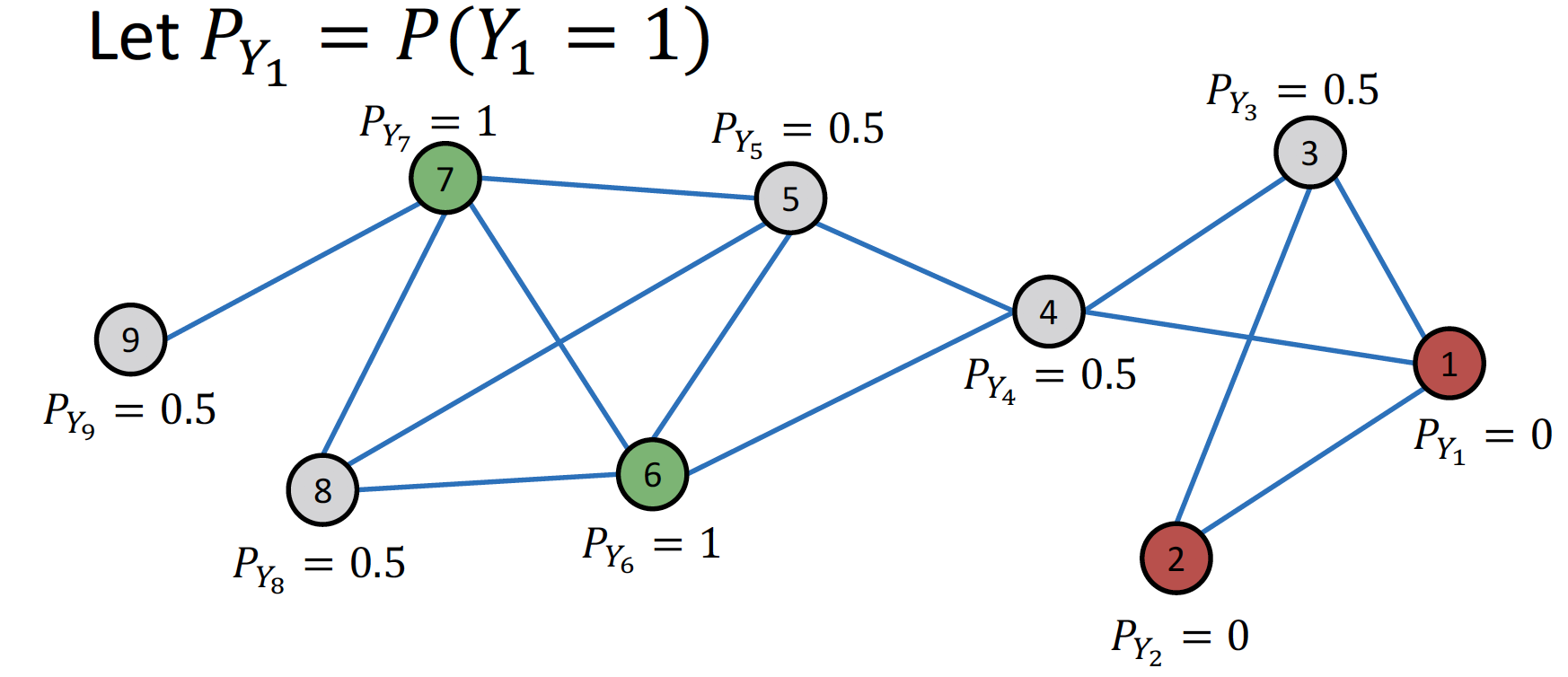
1st Iteration: random order 순서대로 update 합니다.
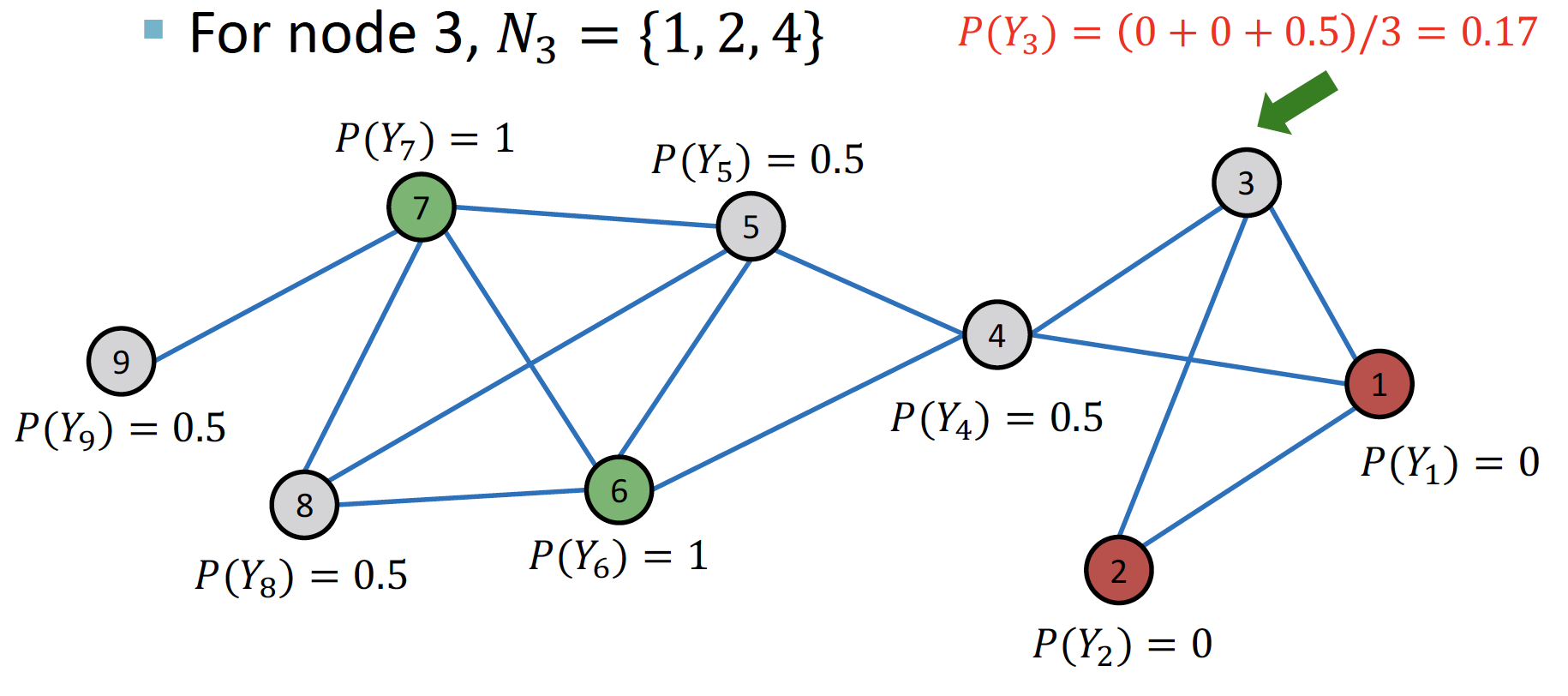
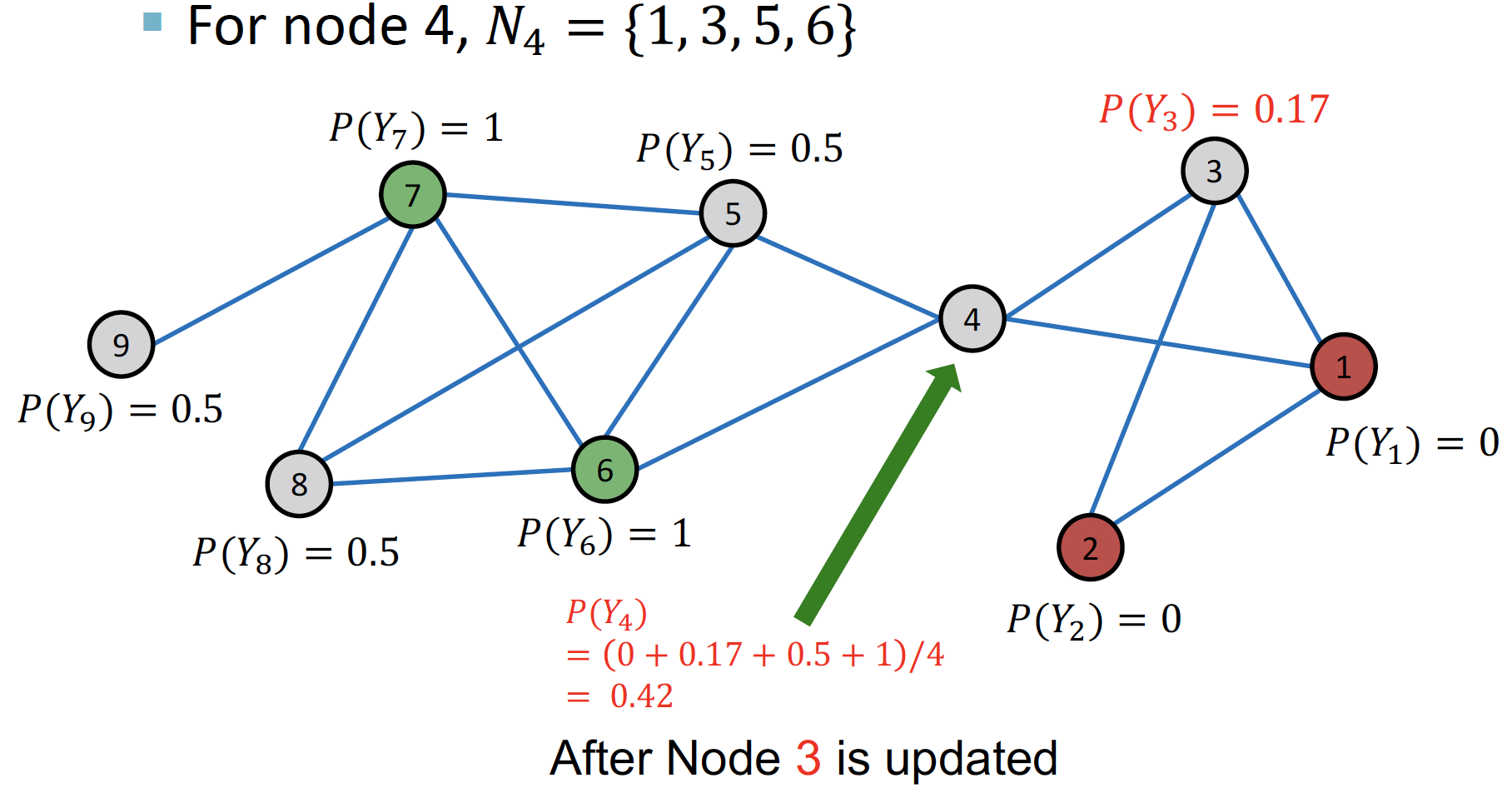
... (node 3→4→5→8→9)
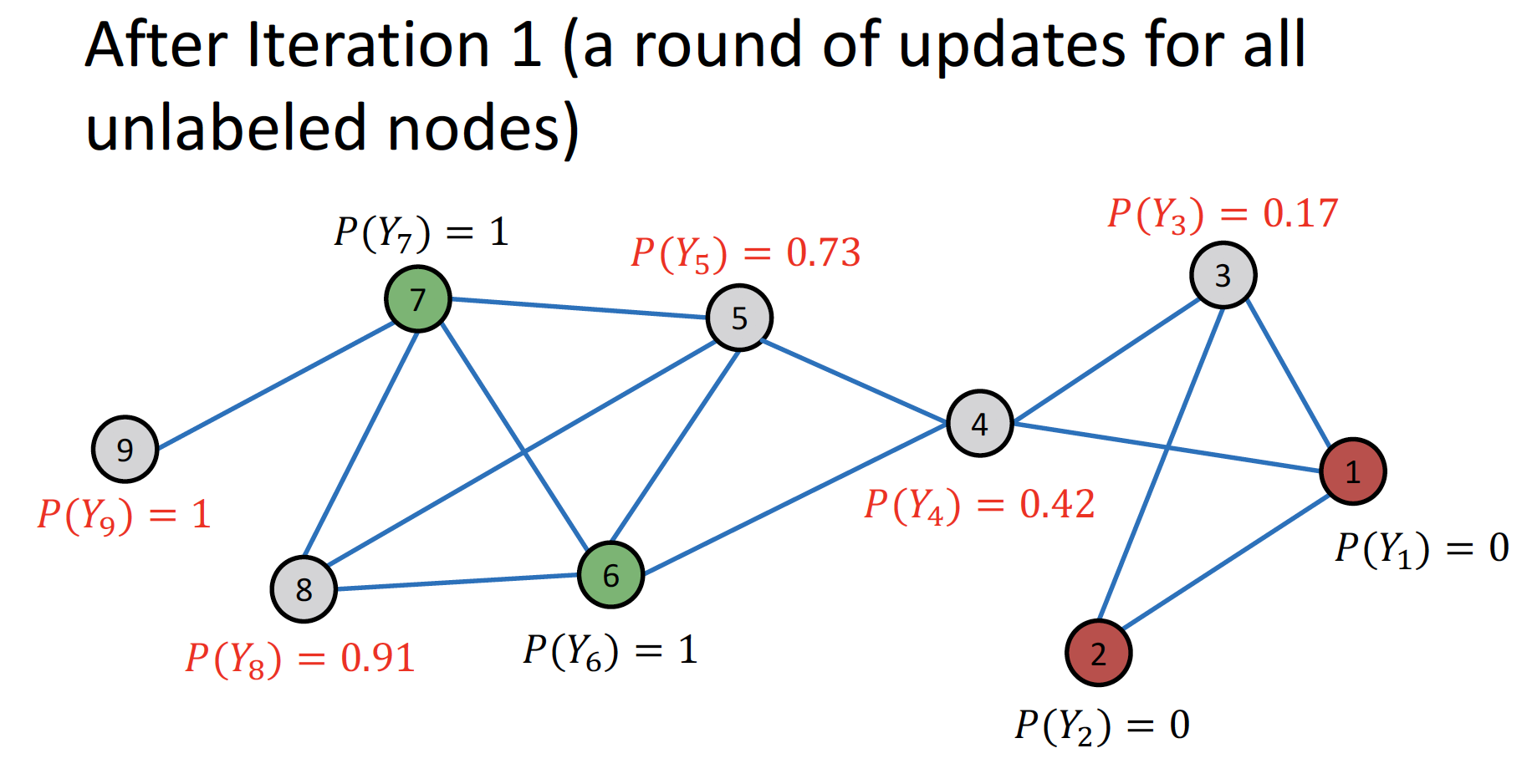
Repeat Iteration: 모든 node 가 수렴할 때 까지 or 최대 iteration 수에 도달할 때 까지 반복합니다.
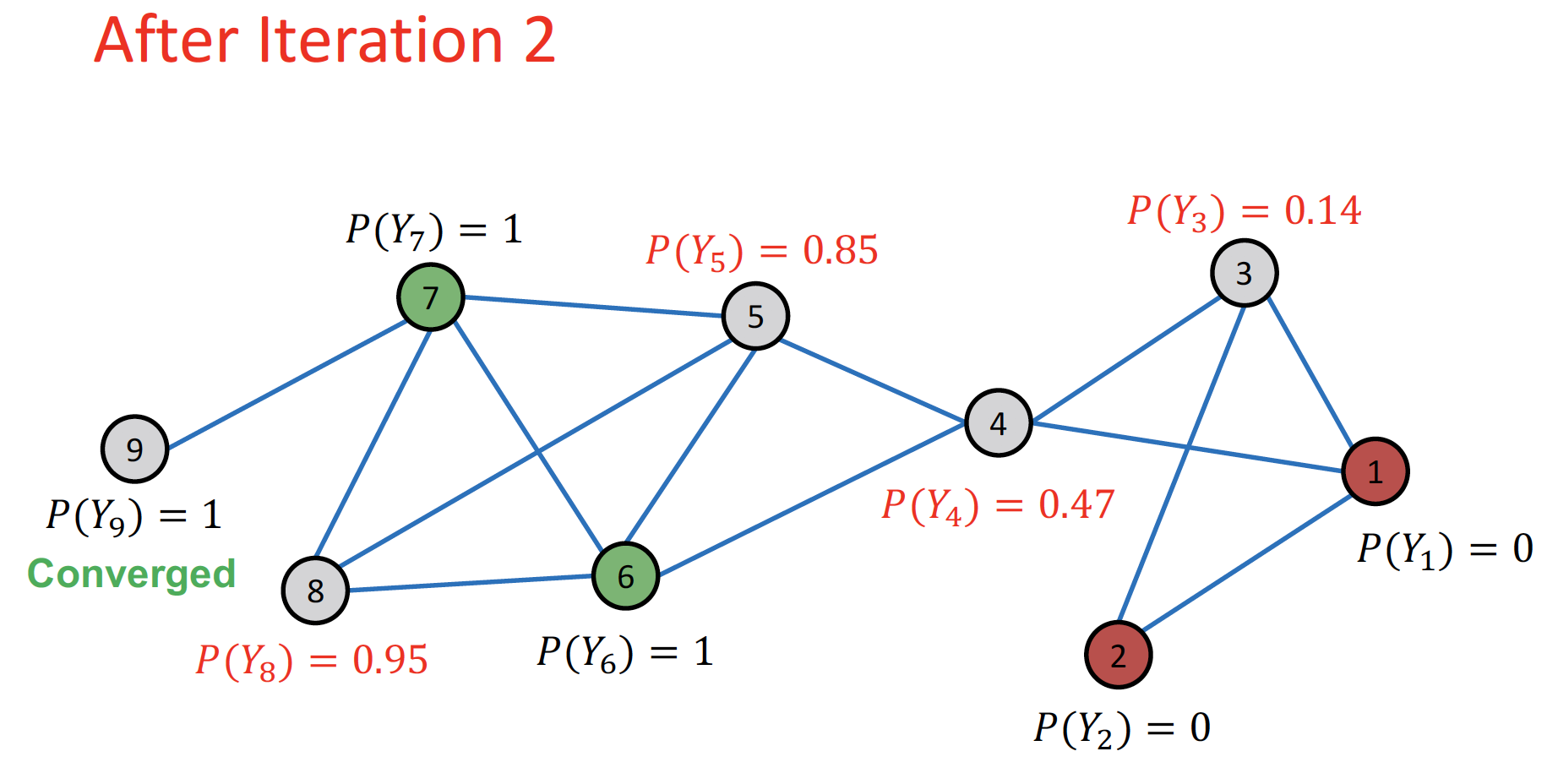
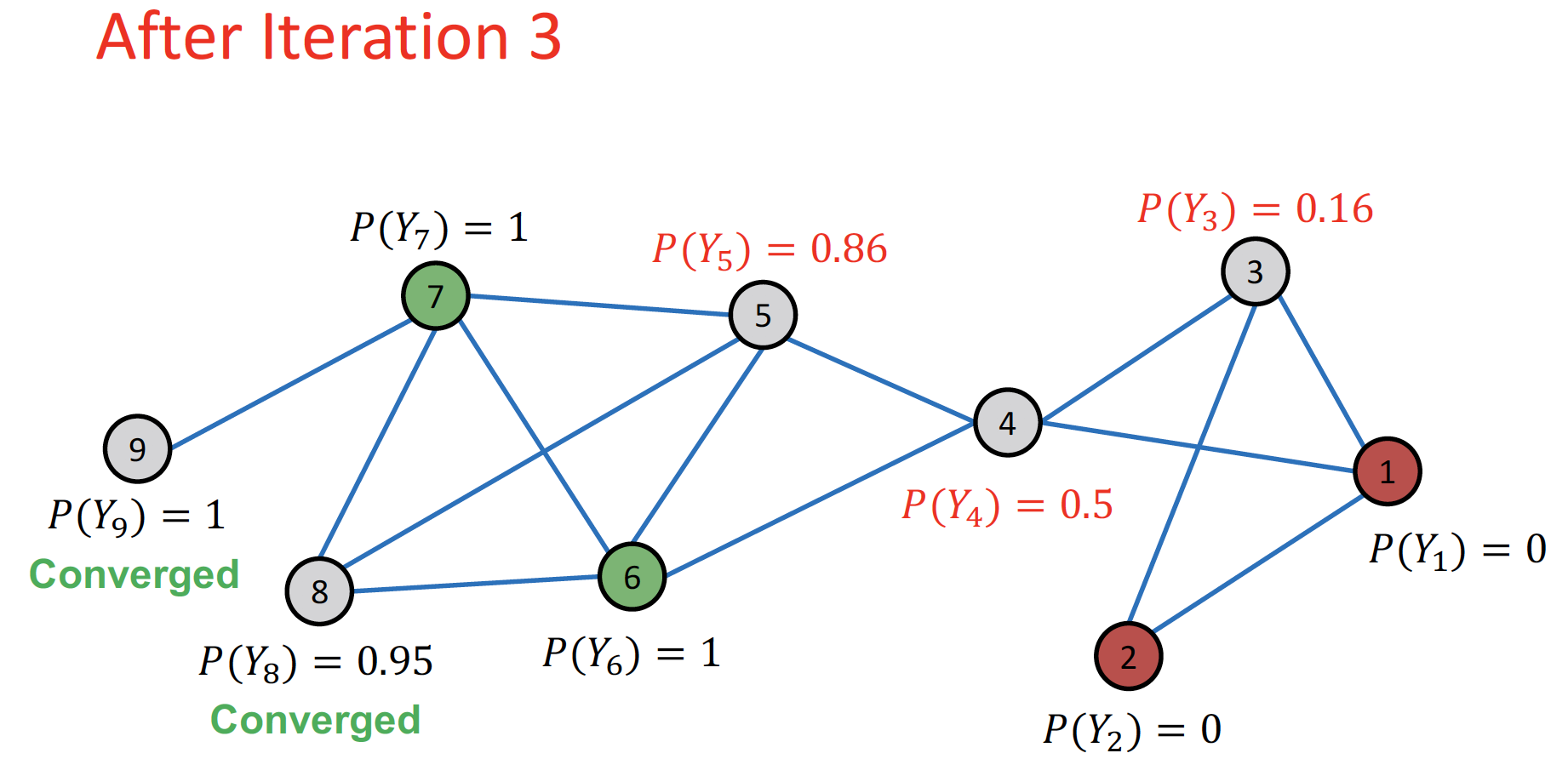
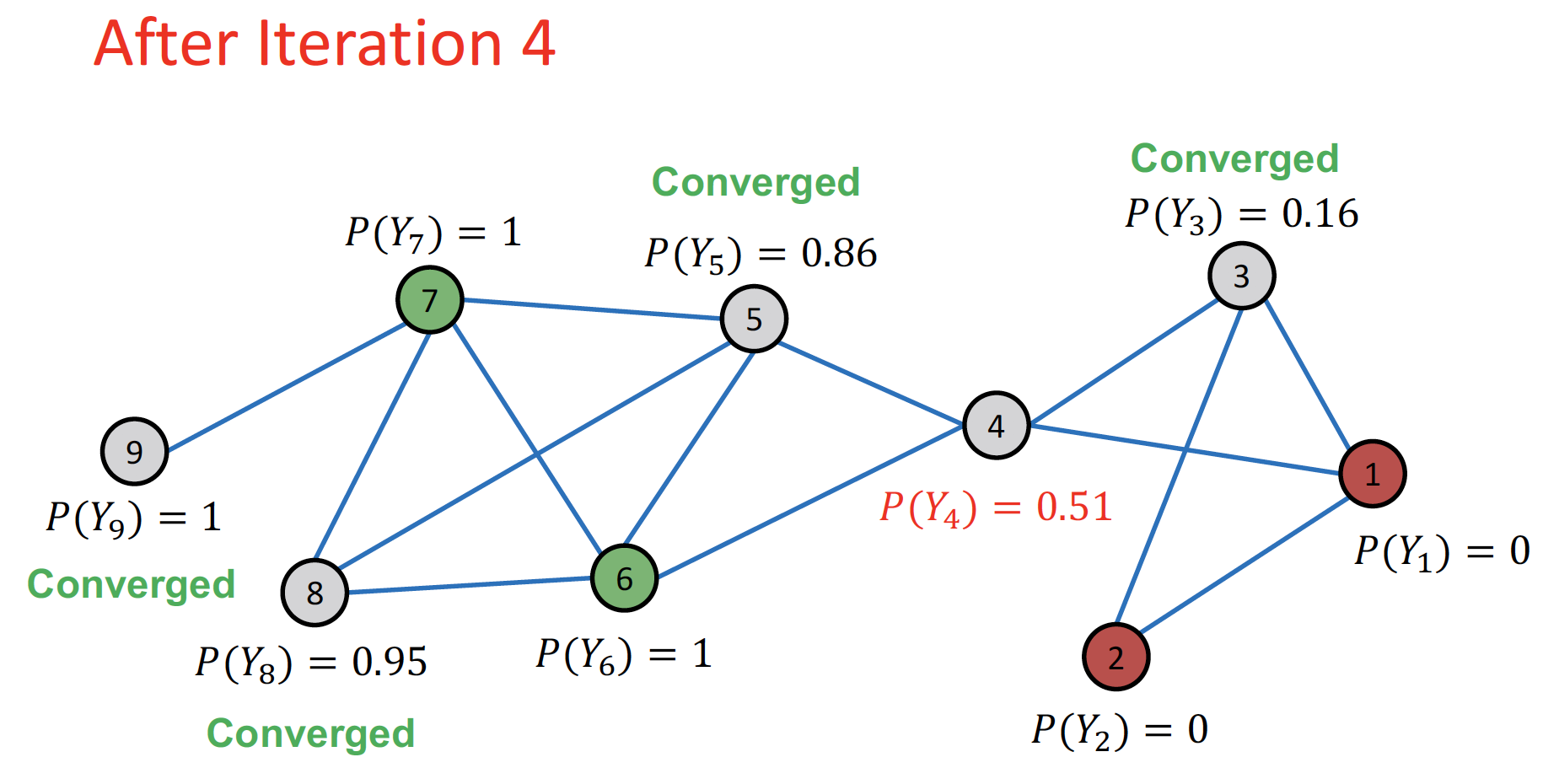
- 인 경우 label = 1, 인 경우 label = 0 으로 분류합니다.
- cf. node 4 : +/- equally contributing → bridge 역할 가능
Challenges
- convergence 보장되어 있지 않습니다. 위의 예시의 경우 그래프가 작아서 수렴이 잘 되었지만, 그래프 크기가 커지는 경우 취약한 방식이라고 합니다.
- node feature information을 전혀 사용하지 않습니다.
2. Iterative Classification
idea : node i의 attribute & neighborhood 의 label 모두 고려합니다.
If two objects are related, inferring something about one object can assist inferences about the other.
PROCESS

- Bootstrap Phase
- : 각각의 node i 에 대해 flat vector 를 생성합니다.
- : 를 local classifier(ex. SVM, KNN, LR) 을 통해 분류합니다.
- aggregate neighbors : count, mode, proportion, mean, exists 등의 neighborhood information 을 취합합니다.
- Iteration phase
- Repeat : 각각의 node i 에 대해 다음 과정을 반복합니다.
- node vector 를 update 합니다.
- 에 대해 label 를 update 합니다.
- Iterate : class label이 stabilize 되거나 최대 iteration 횟수가 만족될 때까지 반복합니다.
- Repeat : 각각의 node i 에 대해 다음 과정을 반복합니다.

- = feature vector 만으로 node label을 예측하는 classifier
- = feature vector + 모두 이용하여 label을 예측하는 classifier

Example : Web Page Classification
-
Setting
- : feature vector, node의 정보
(강의에서 소개해 준 feature vector 예시 : Bag-Of-Words) - : neighborhood label에 대한 정보 통계량 벡터
- I : Incoming neighbor label information vector
- O : Outgoing neighbor label information vector
- = 1 : 최소 1개의 label 0 노드가 incoming (count)
- : feature vector, node의 정보
-
과 를 학습시킵니다.
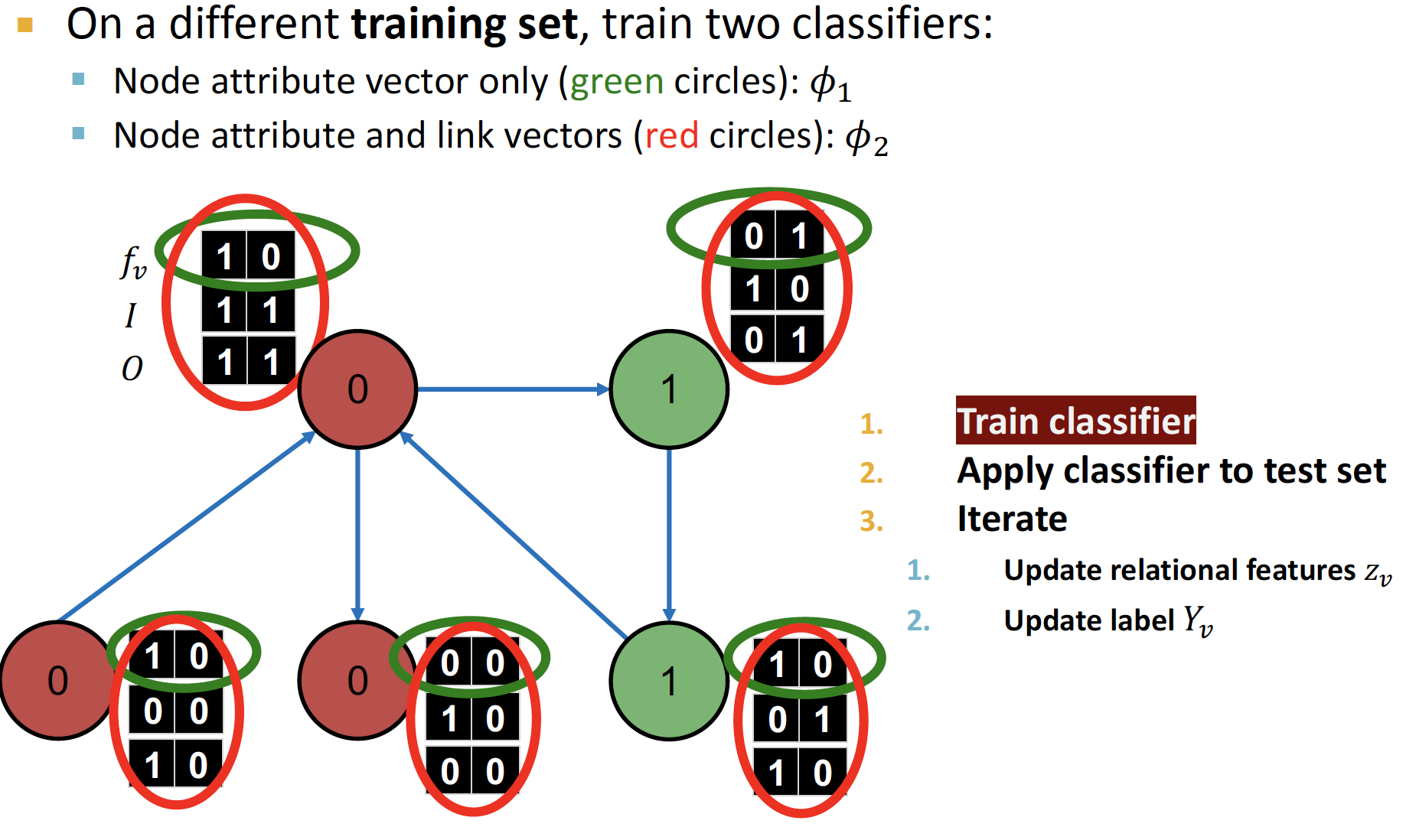
-
feature vector 만으로 classification () 을 진행합니다.
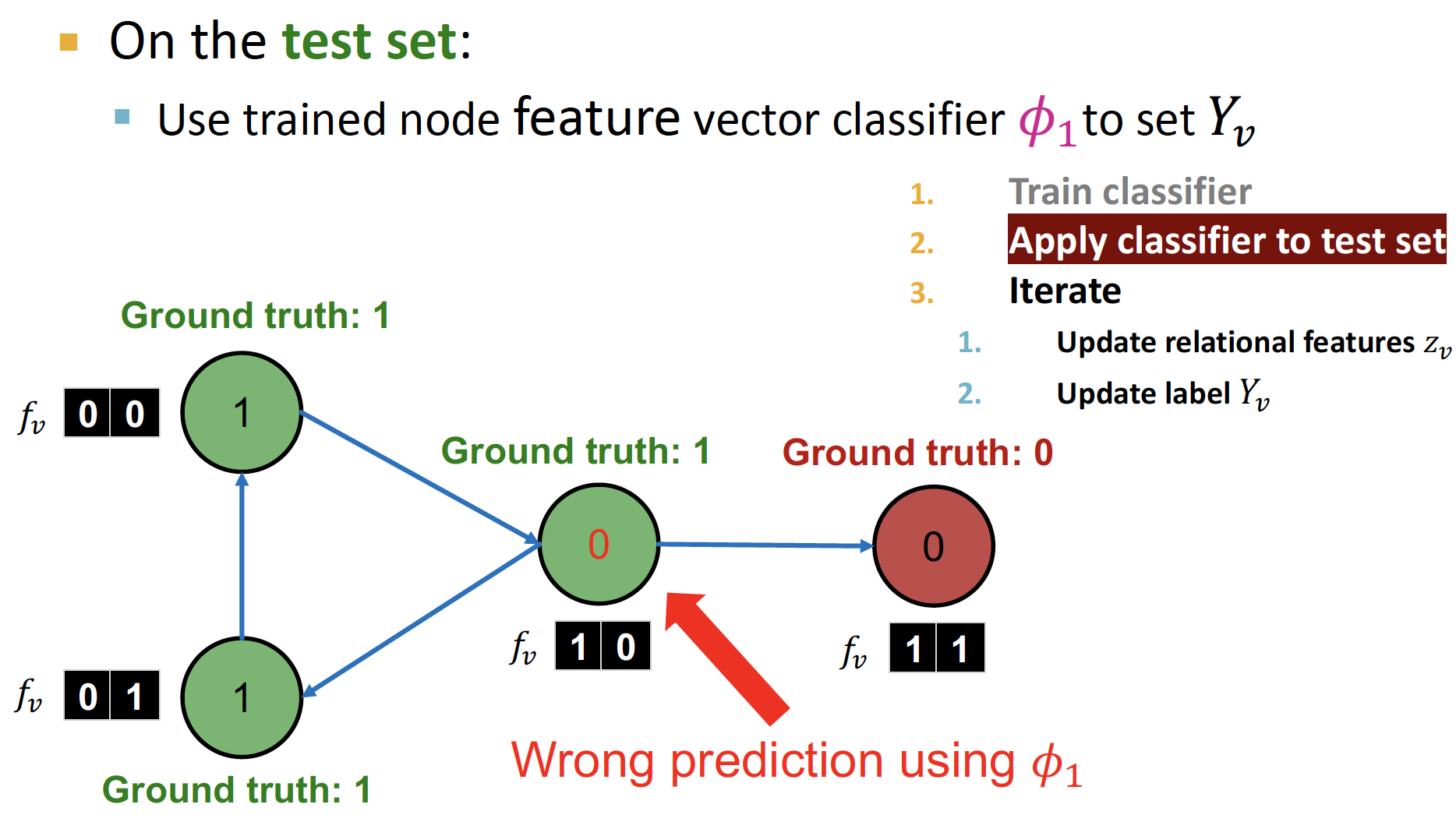
-
예측한 label 값에 기반하여, 를 update 합니다.
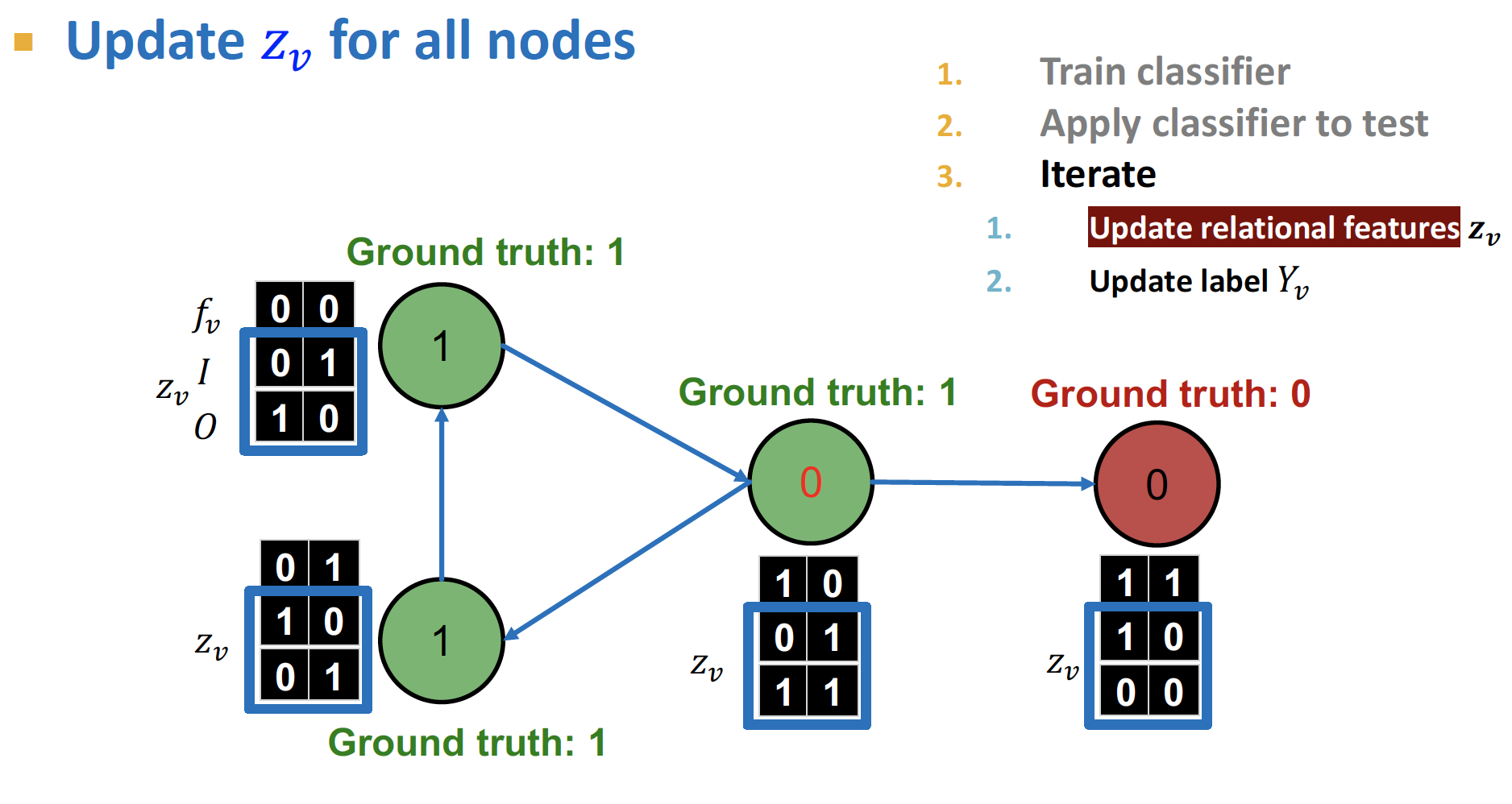
-
feature vector와 를 모두 사용하여 classification () 을 진행합니다.
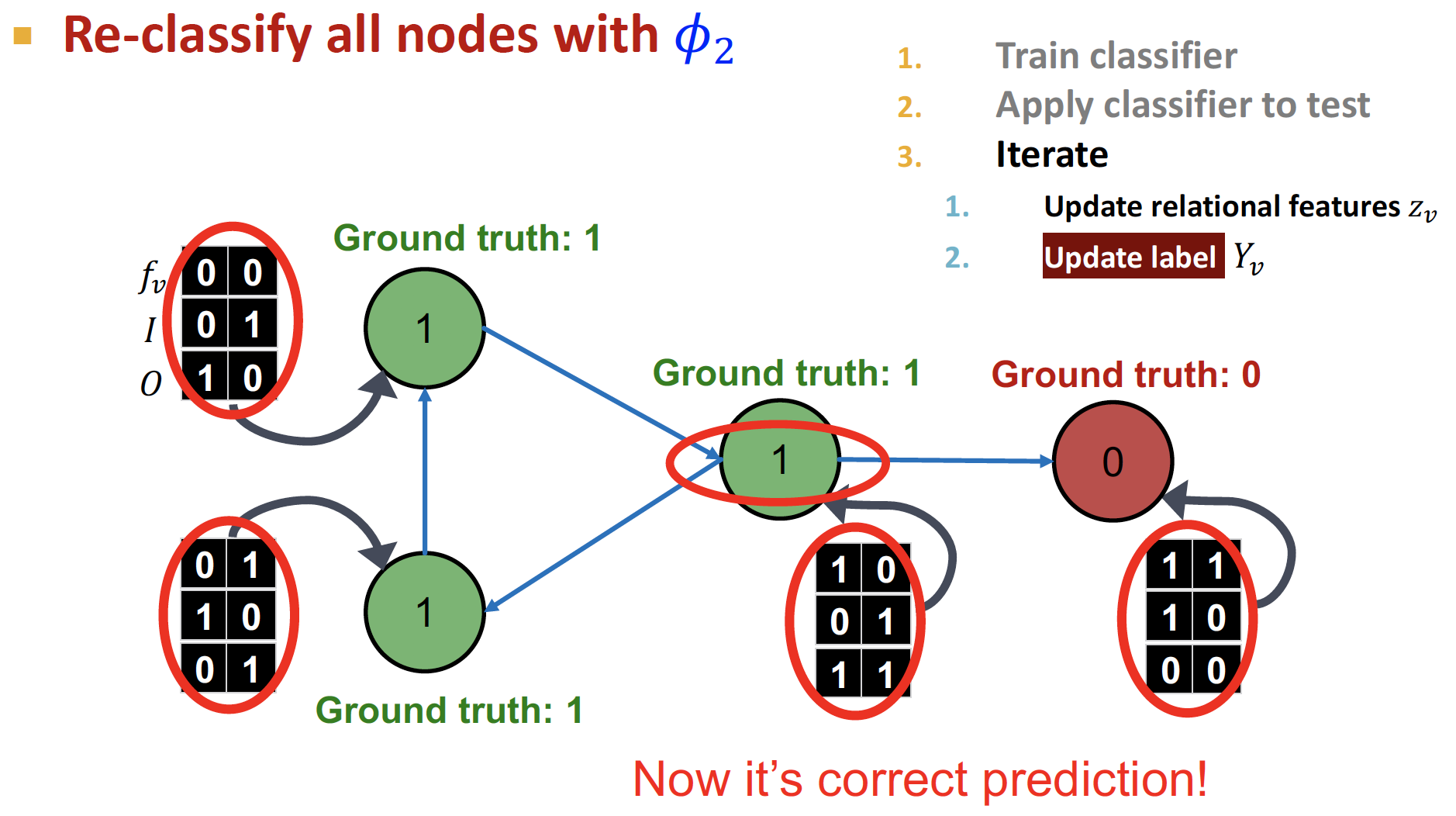
-
수렴할 때 까지 반복합니다.
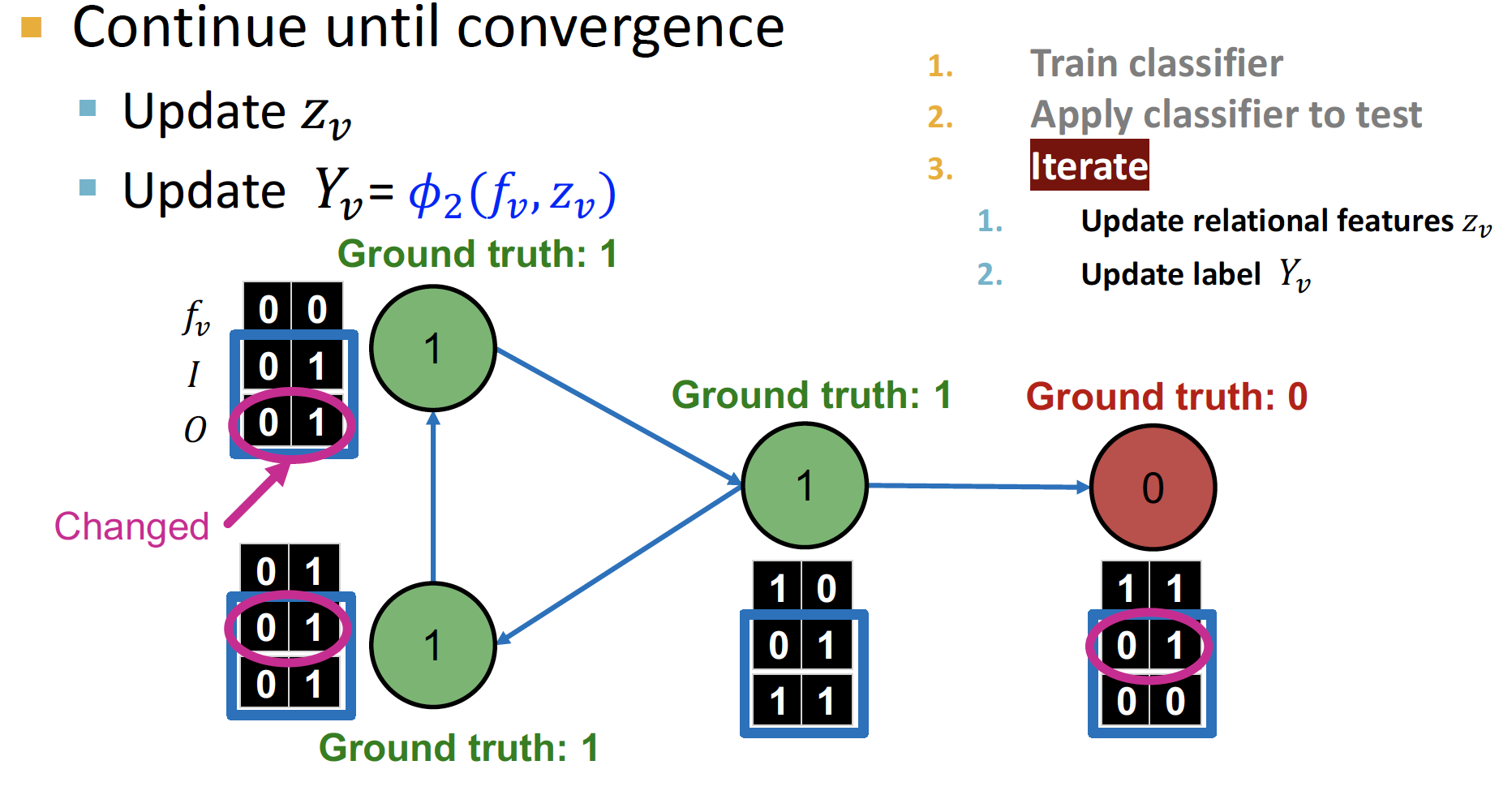
REV2 : Fake Review Detection
Fake Review Spam
- Review Site에서는 spam이 공공연하게 발생합니다.
- 평점이 하나 높아질수록, 수입이 5~9% 상승합니다.
- Paid Spammers는 거짓으로 해당 상품들의 평가를 낮게 평가함으로써, 경쟁사를 꺾으려고 합니다.
- Behavioral analysis, Language Analysis 만으로는 Spammer를 판별하기 어려운데, Individual Behavior 이나 Content of Review 는 거짓으로 보여주기 쉽기 때문입니다.
- 따라서, 쉽게 속이기 어려운
graph structure를 통해 Reviewers, Reviews, Stores 사이의relationship을 파악하고자 합니다.
REV2 Solution
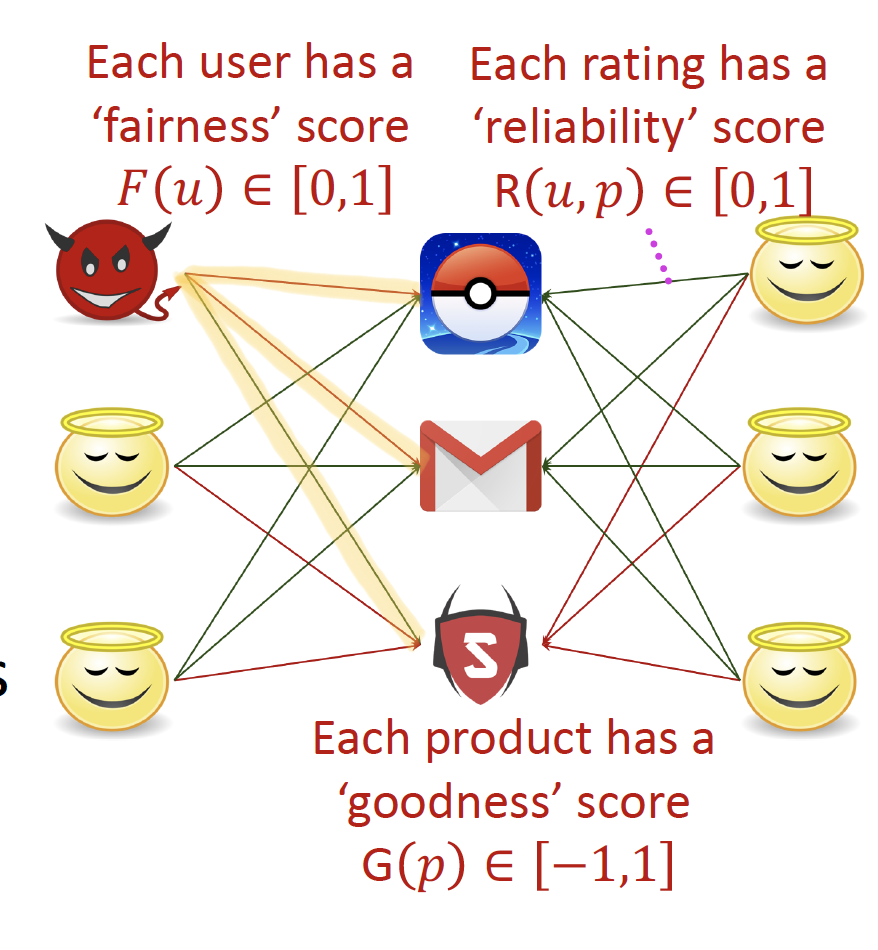
- Setting
Input: Bipartite rating graph as a weighted signed networknode: Users, Products (Items)Edges: [-1, +1] rating scores (Red : -1 & Green : +1)
Output: 거짓으로 평점을 평가하는 유저 집단
- Intrinsic Properties
- Users have
fairnessscores
사기꾼들은 좋은 상품에 낮은 평점, 나쁜 상품에 좋은 평점을 줄 것입니다. - Products have
goodnessscores
좋은 상품의 평점은 좋을 것입니다. - Ratings have
reliabilityscores
reliability fairness : user는 bias가 있습니다.
개인적인 의견이 다수의 의견과 일치하지 않을 수 있습니다.
- Users have
- Axiom
- Better Products get higher ratings.
- Better products get more reliable positive ratings.
- Reliable ratings are closer to goodness scores.
- Reliable ratings are given by fairer users.
- Fairer users give more reliable ratings.
Iterative Classification
-
Fairness of Users : goodness와 reliability를 고정시키고, fairness를 update 합니다.
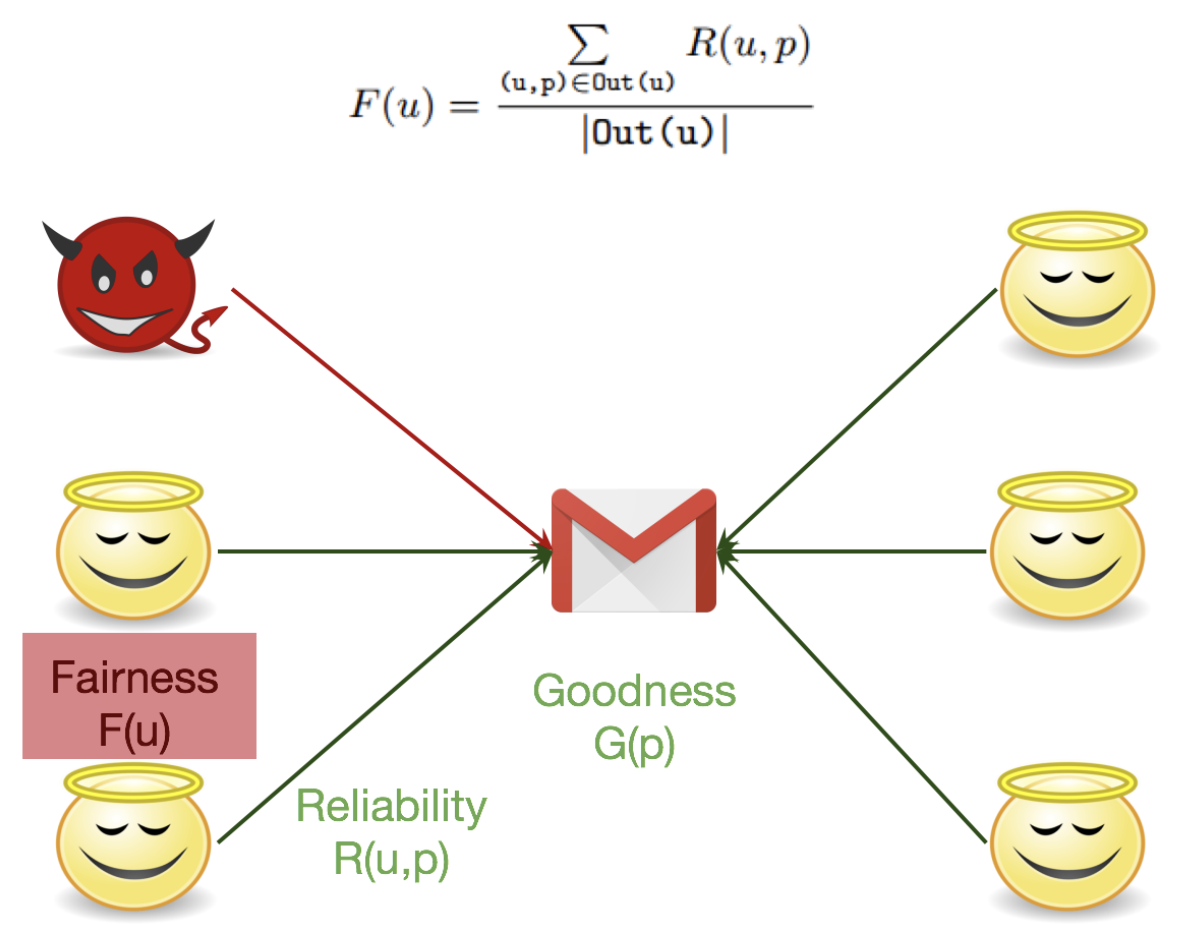
-
Goodness of Products : fairness와 reliability를 고정시키고, goodness를 update 합니다.
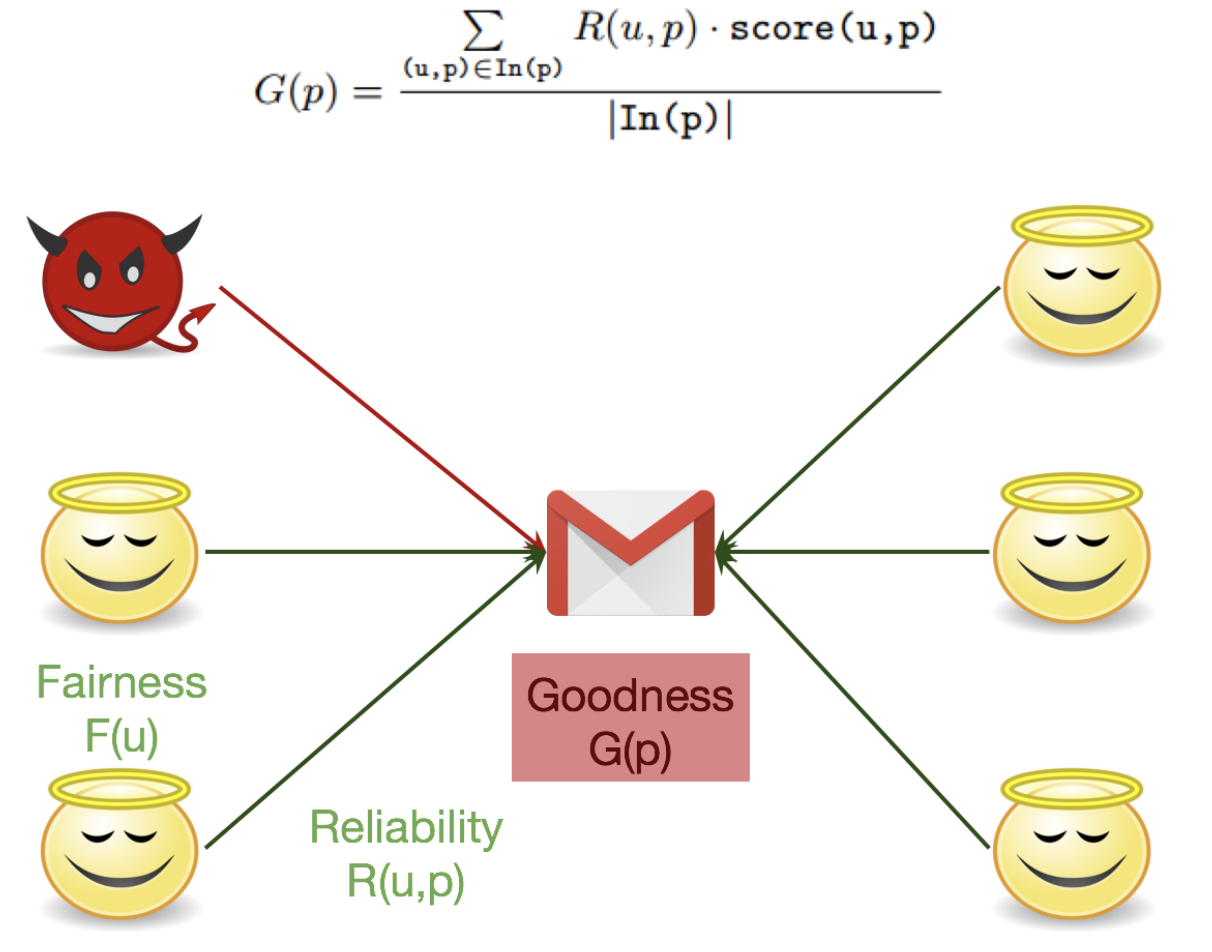
-
Reliability of Ratings : fairness와 goodness를 고정시키고, reliability를 update 합니다.
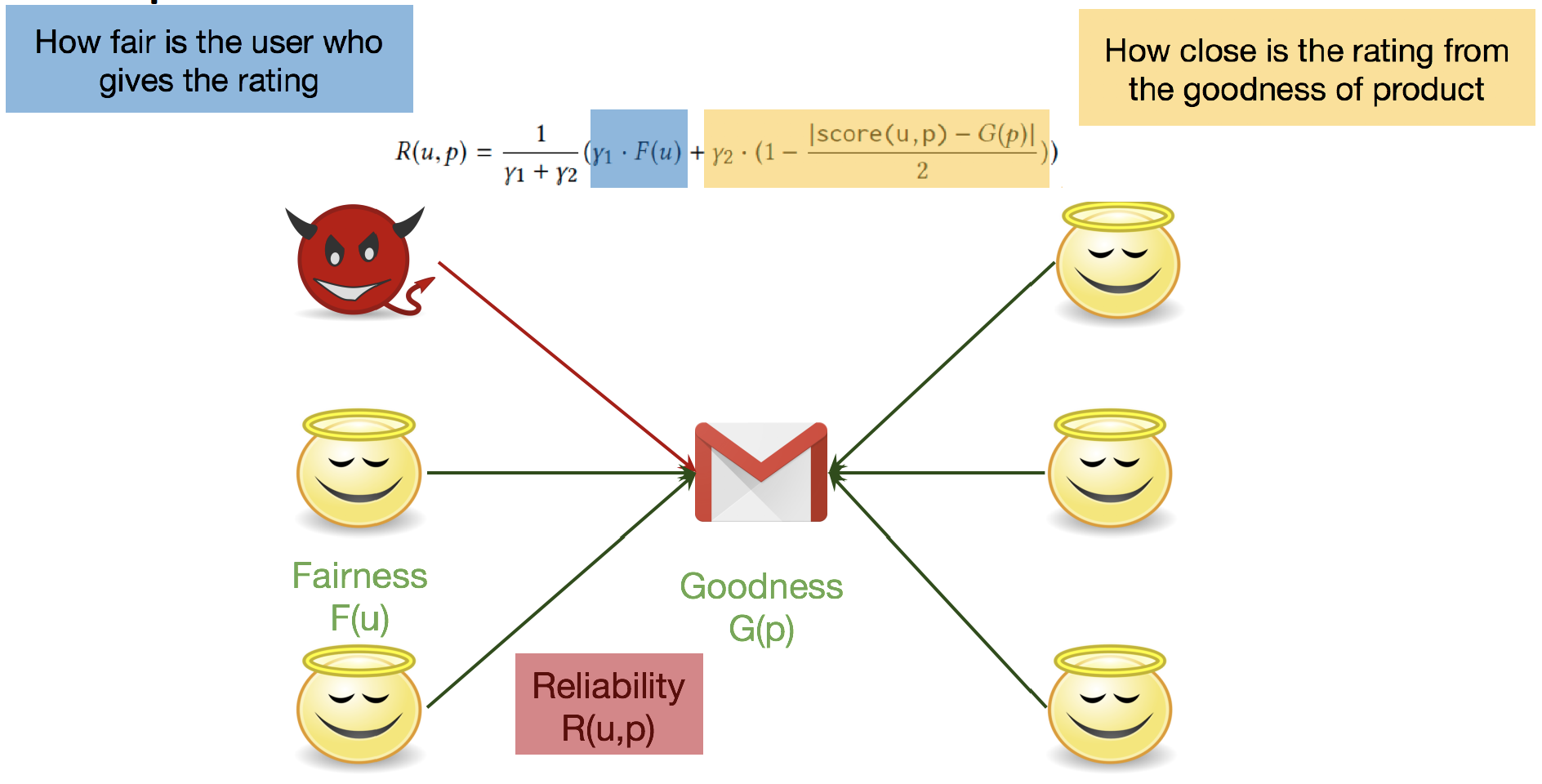
PROCESS
-
Initialize to best scores : F, G, R 값을 모두 1로 초기화합니다.
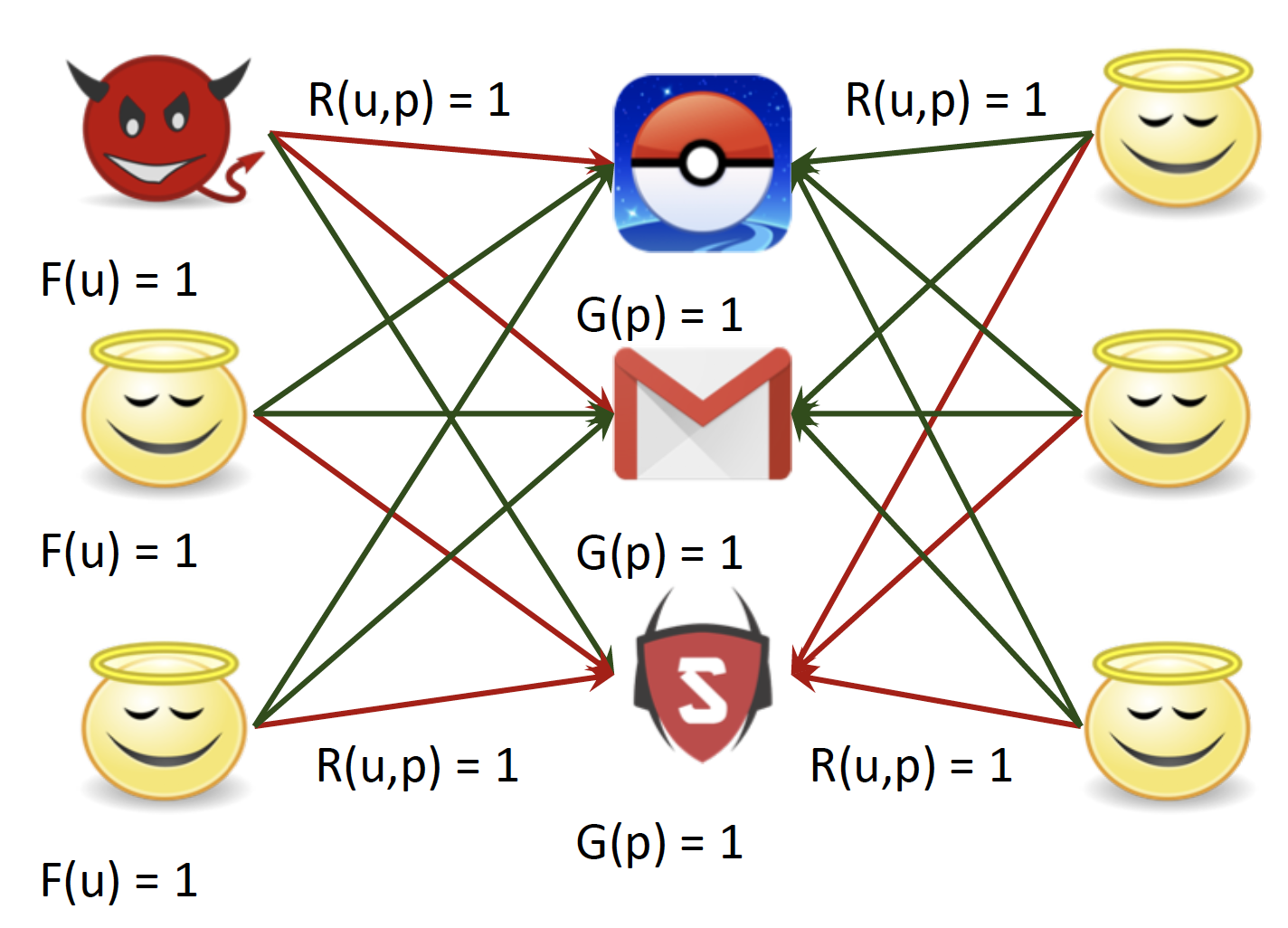
-
Updating goodness
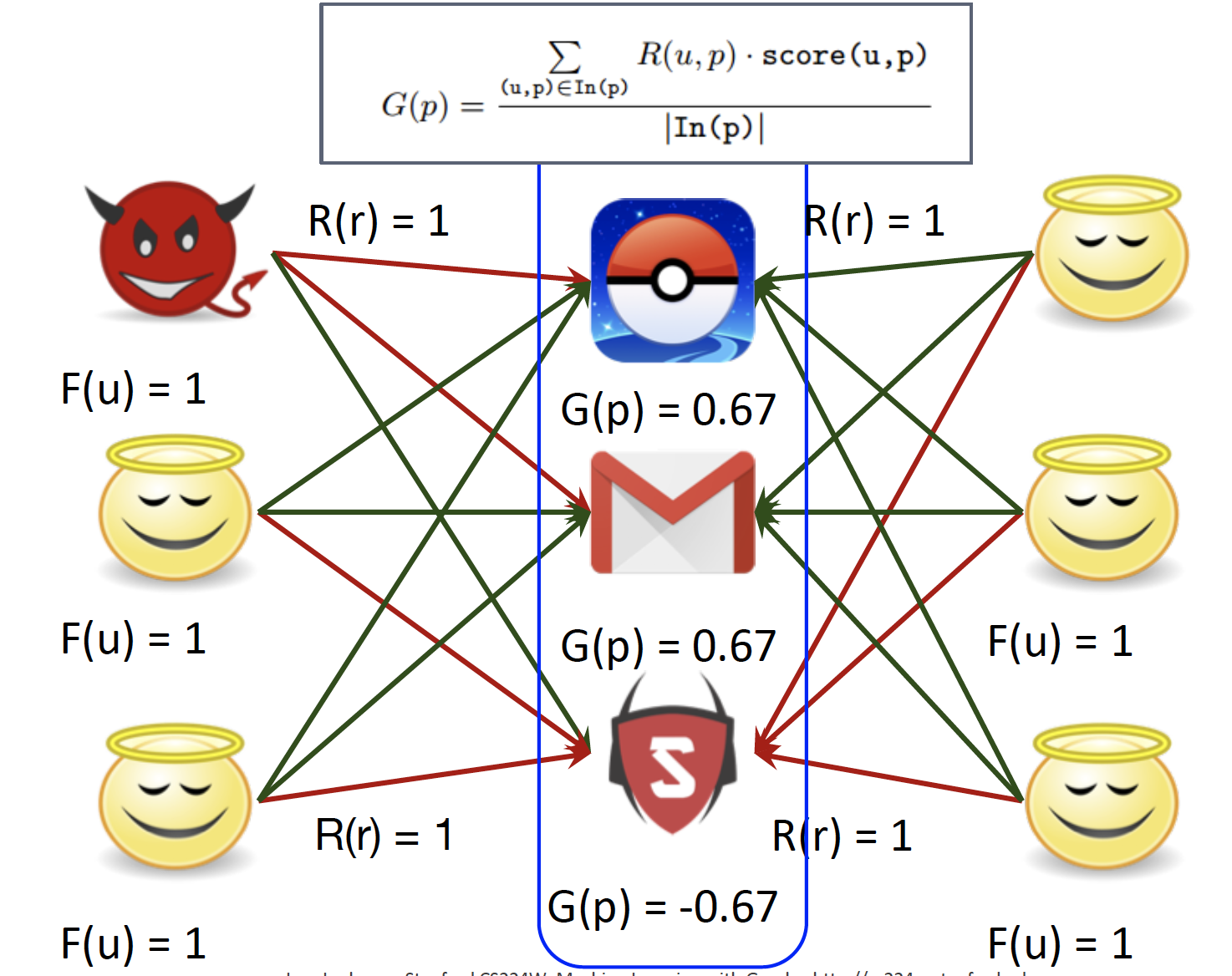
-
Update reliability
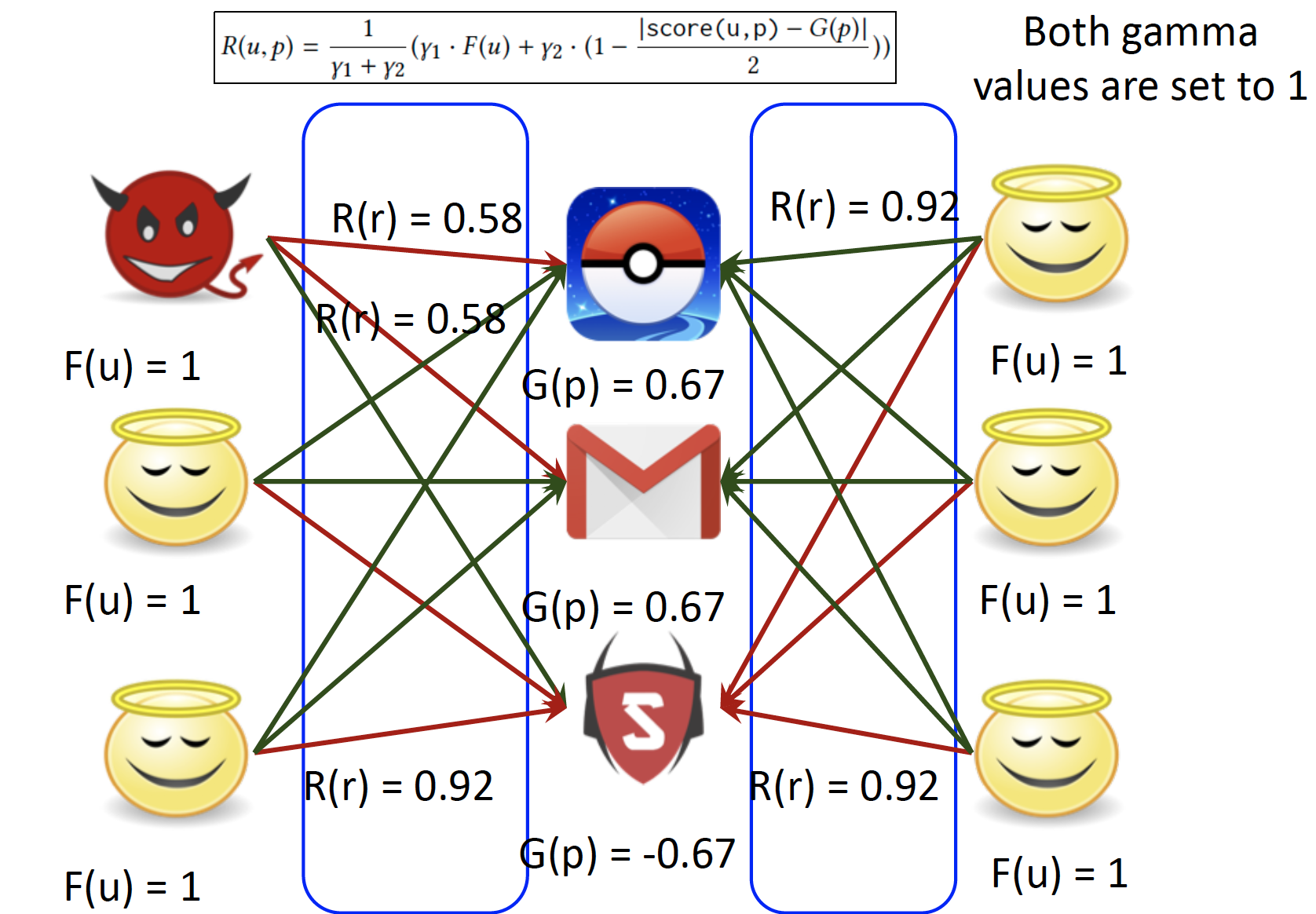
-
Update fairness
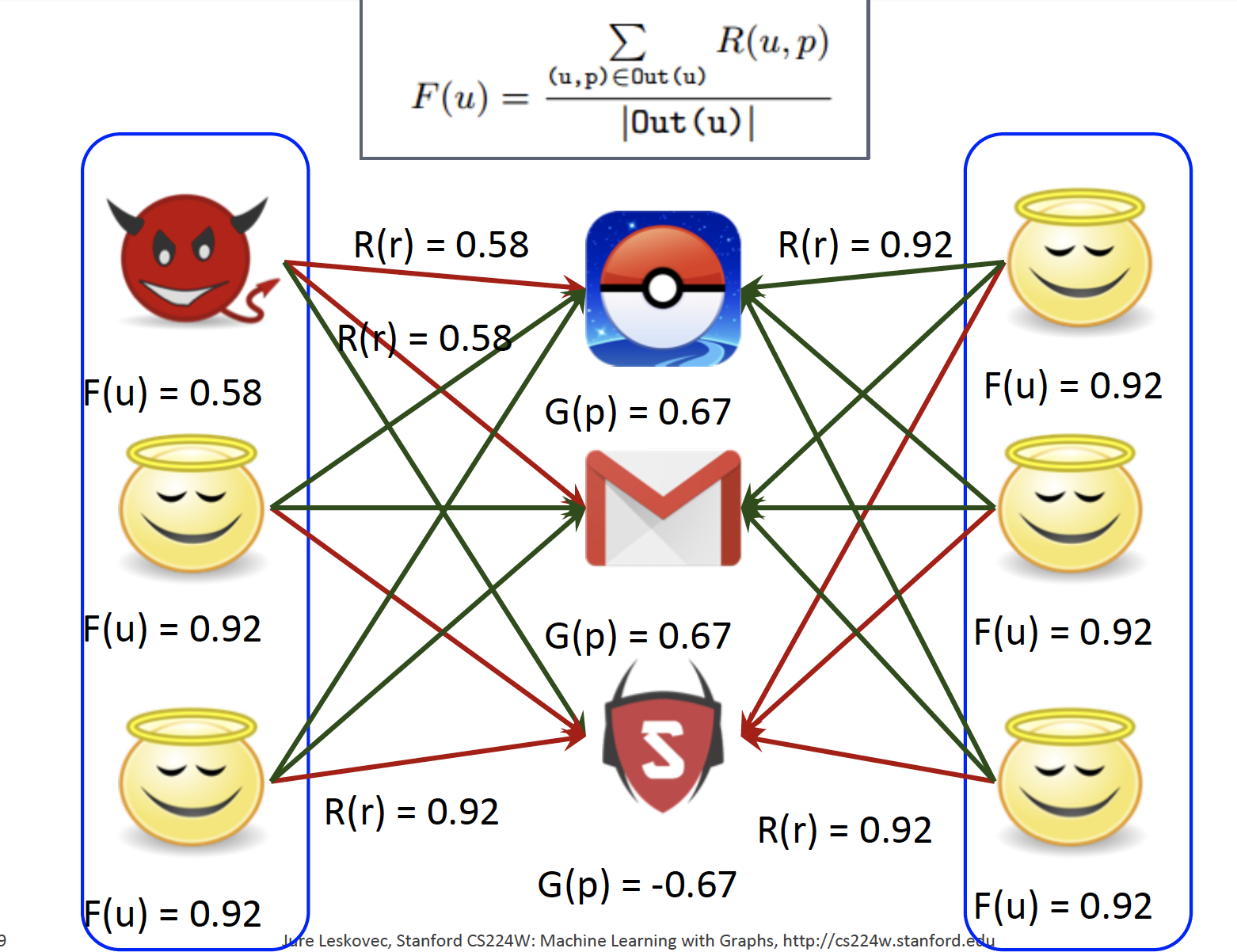
-
Convergence : Fairness가 낮은 user가 Fraudster 입니다.
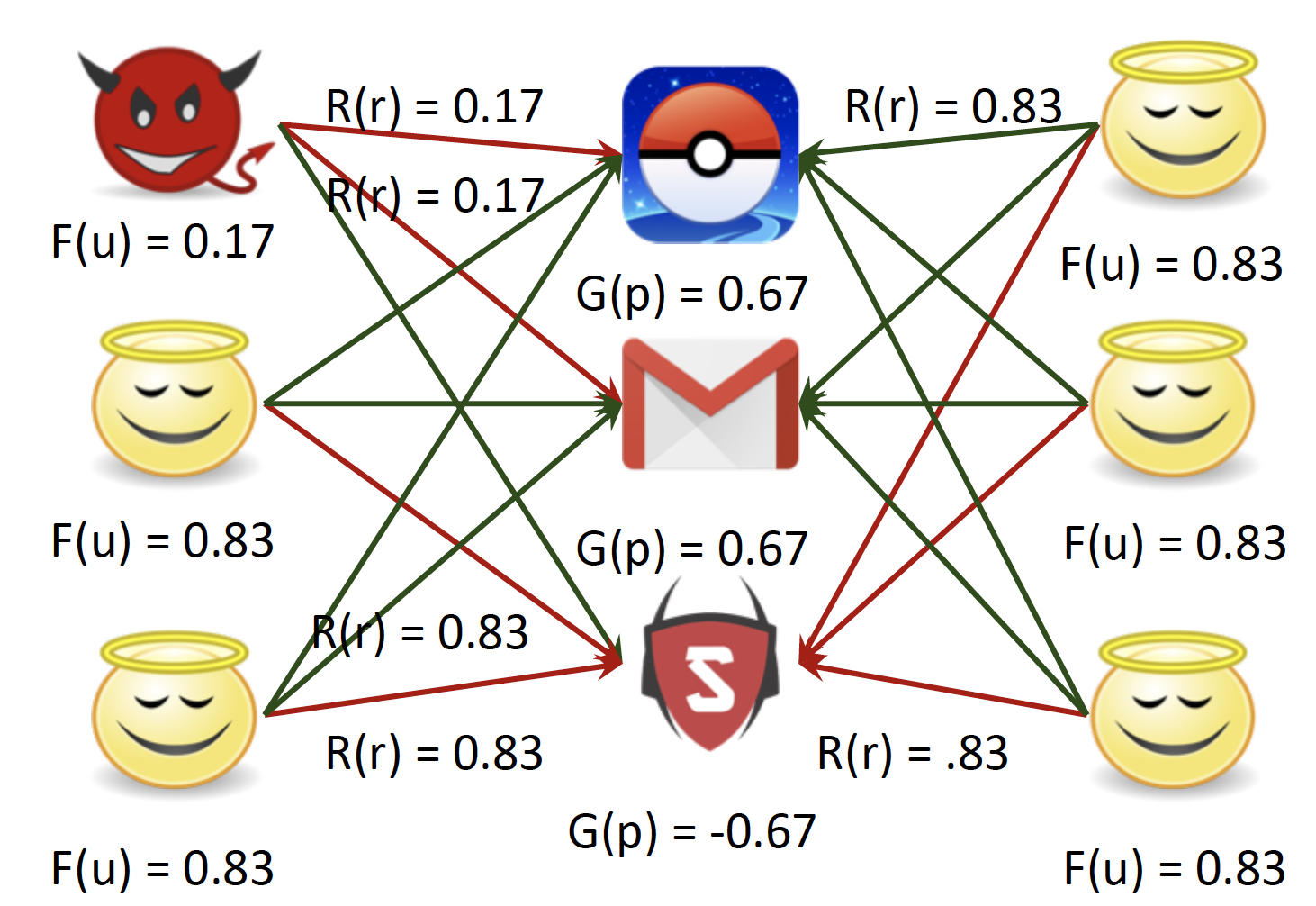

Properties of REV2 Solution
- REV2는 수렴이 보장되어 있습니다.
- 수렴하기까지 총 Iteration 횟수의 상한선이 존재합니다.
- 시간복잡도는 그래프의 Edge의 수가 증가함에 따라 Linear하게 증가합니다.
- 위에서 다루지는 않았지만, Laplace Smoothing을 통해 cold start problem도 해결합니다.
3. Belief Propagation
idea : message passing
dynamic programming 접근 방식으로, graph model에서 조건부 확률로 답을 구해내는 방식입니다.
Message Passing

- Task : graph 에서 node의 개수 세기
- Condition : 각 node들은 그들의 neighbors와만 interact 할 수 있습니다.
- Solution : 각 node들은 그들의 neighbor로 부터 message를 전달받고, 이를 update 하여, 앞으로 전달합니다.
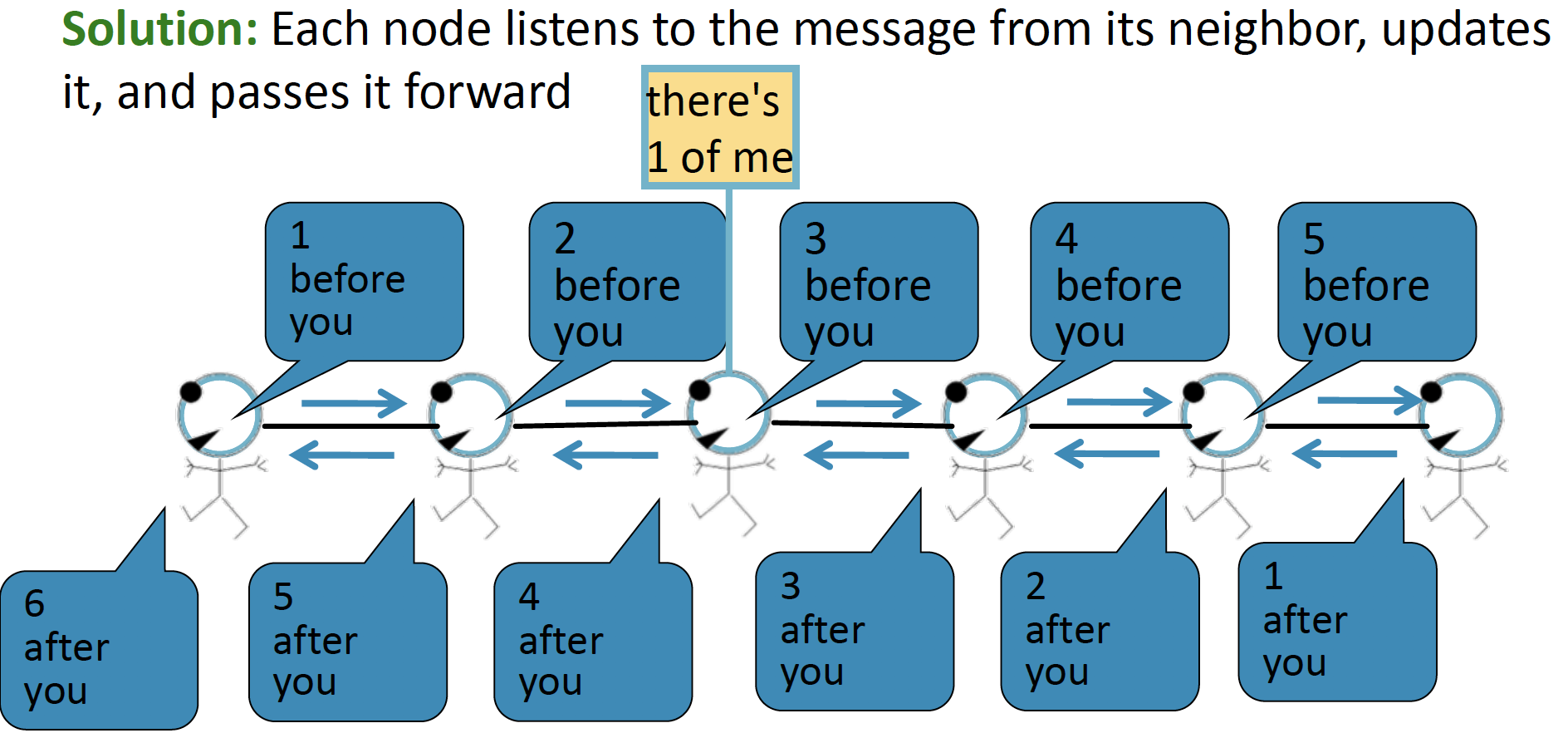
Message Passing in Trees
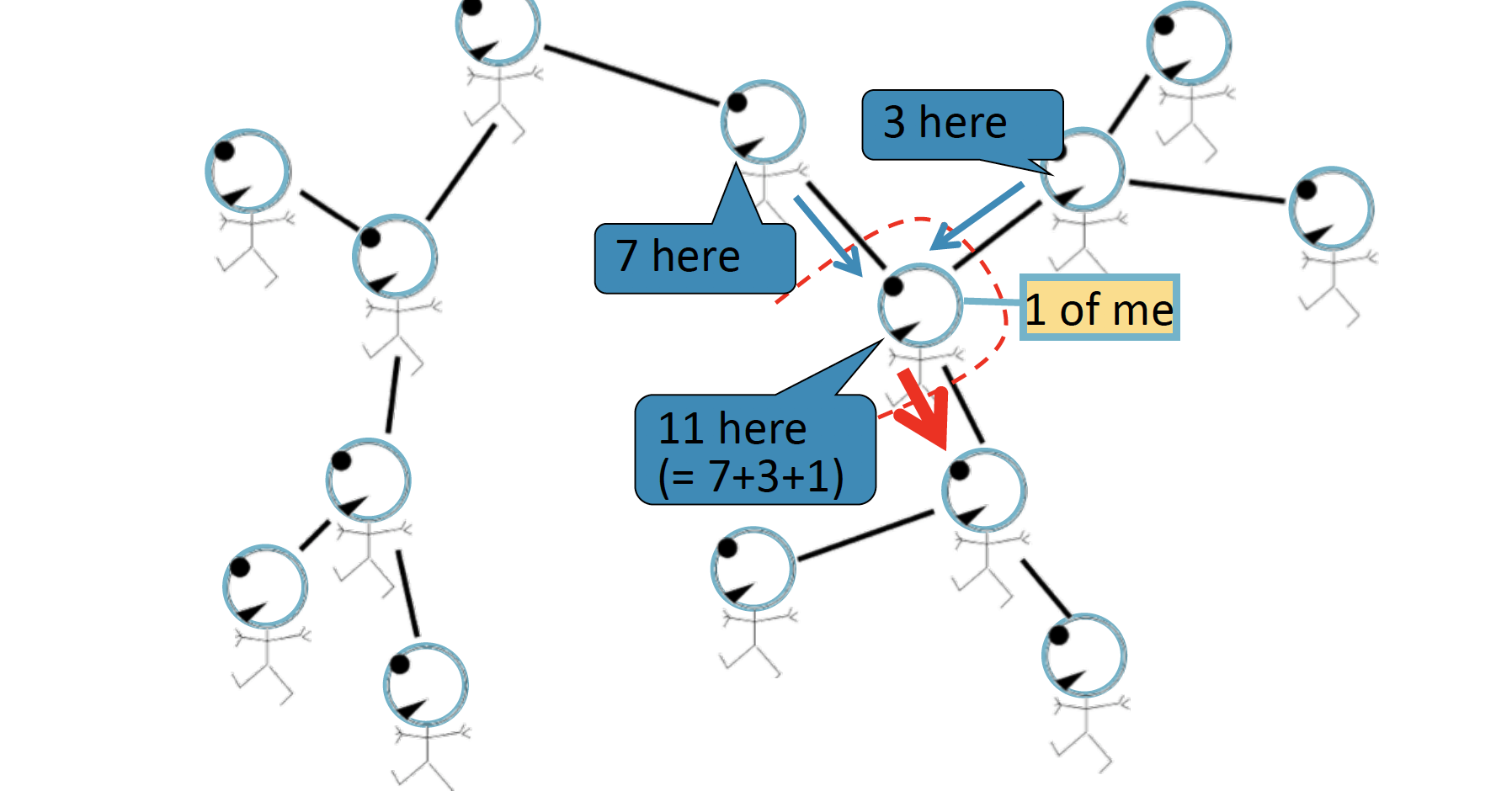
노란색 node에서 전달된 정보를 토대로 개수를 파악하여, 앞으로 전달합니다.
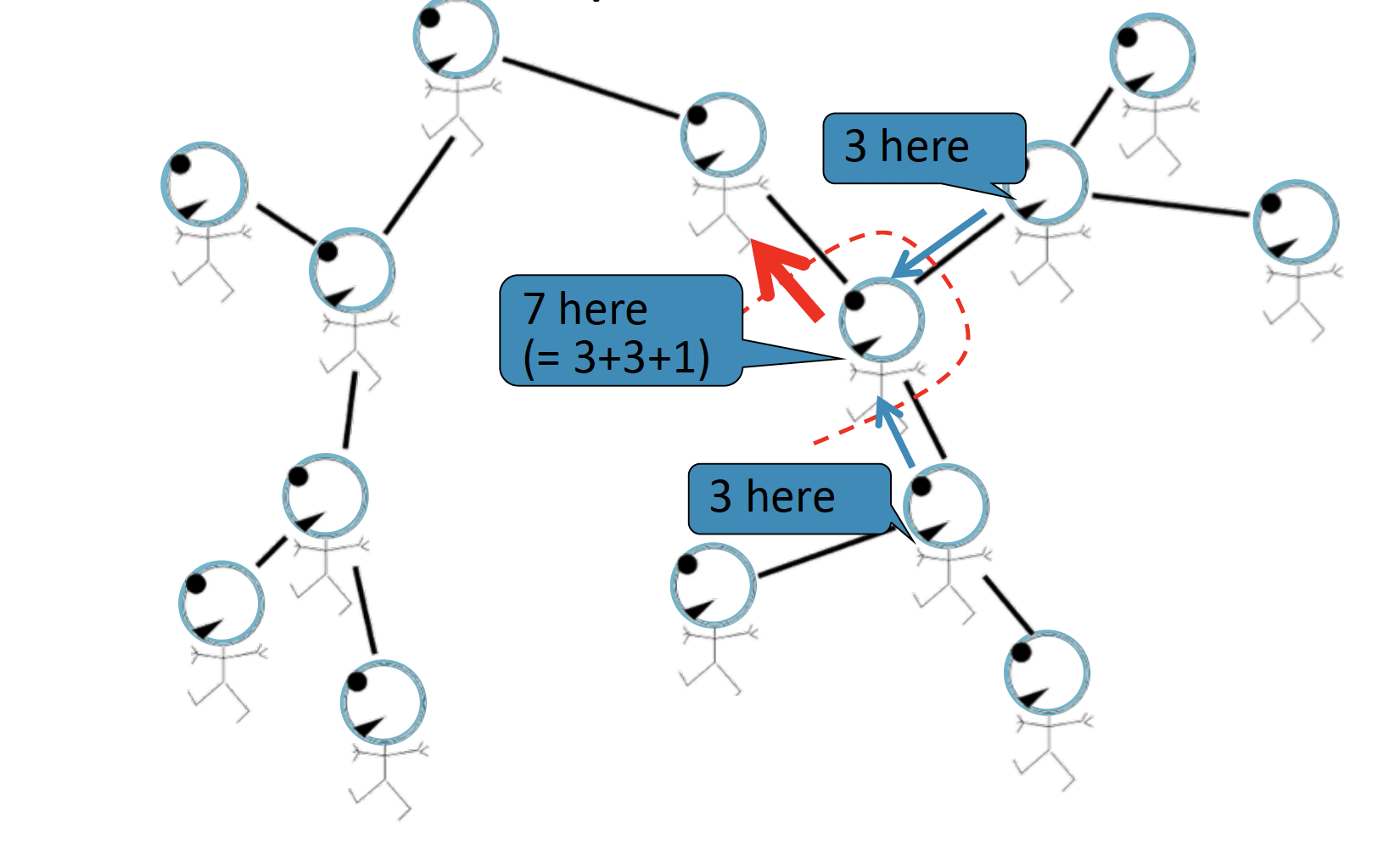
반대 방향으로 전달할 때에는, 위와 같습니다.
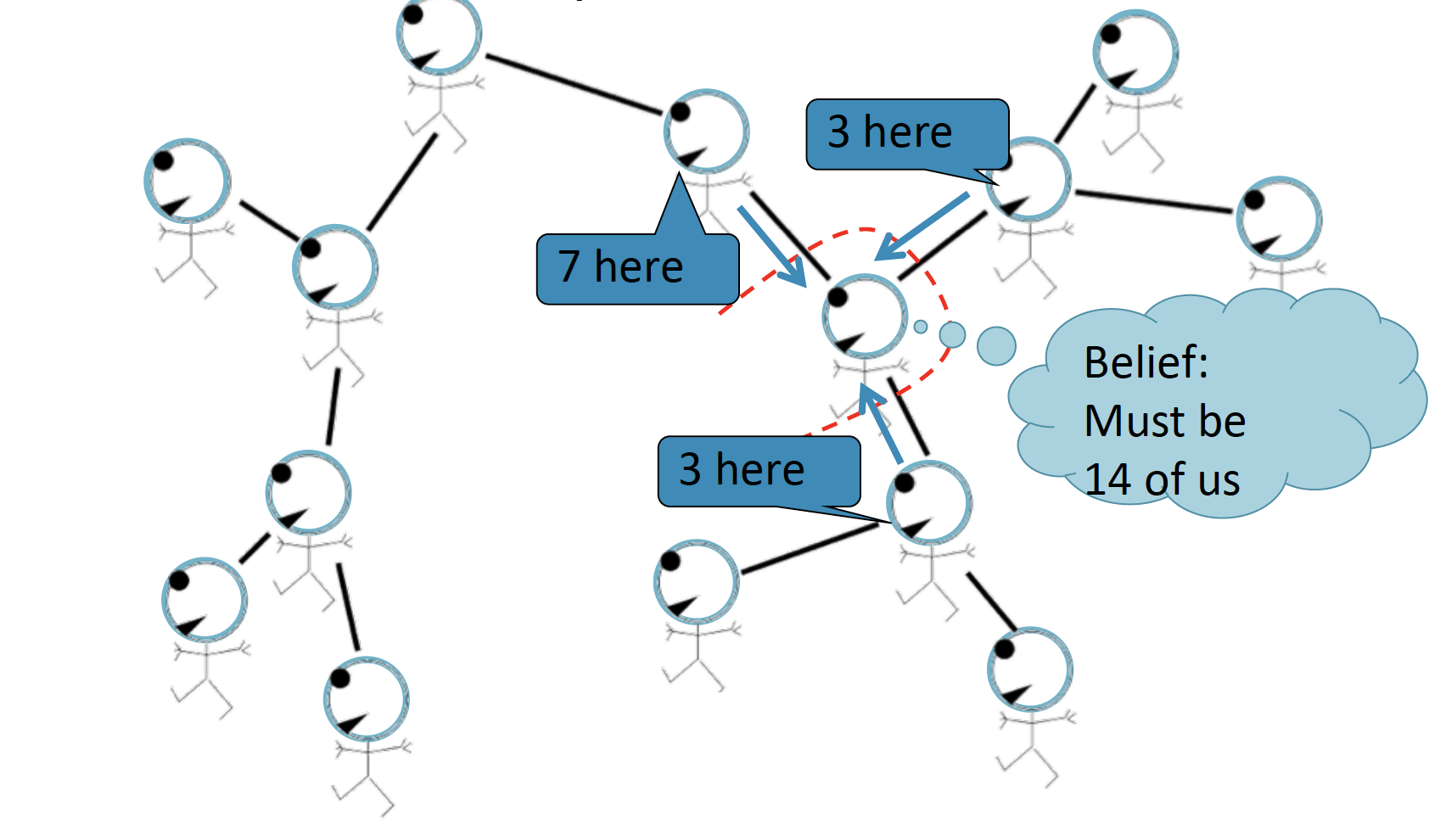
따라서 전달된 (Passing a belief) 두 정보를 종합하여, 7+3+3+1=14 라는 과정을 통해 총 node의 개수는 14개가 될 것이라는 Belief Propagation 을 내리게 됩니다.
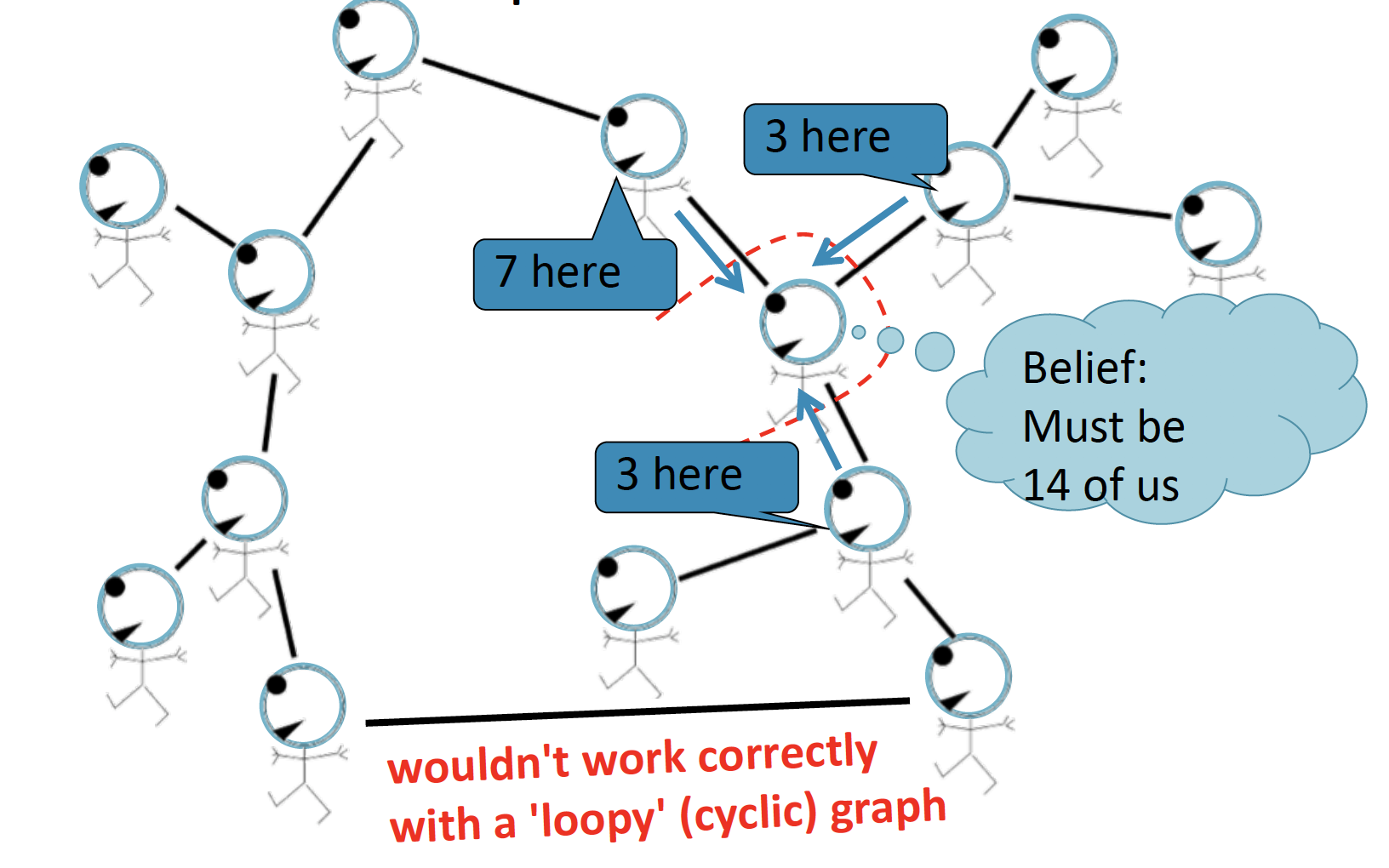
다만, graph가 cyclic 한 경우에는 Belief Propagation이 잘 작동하지 않습니다.
Loopy Belief Propagation
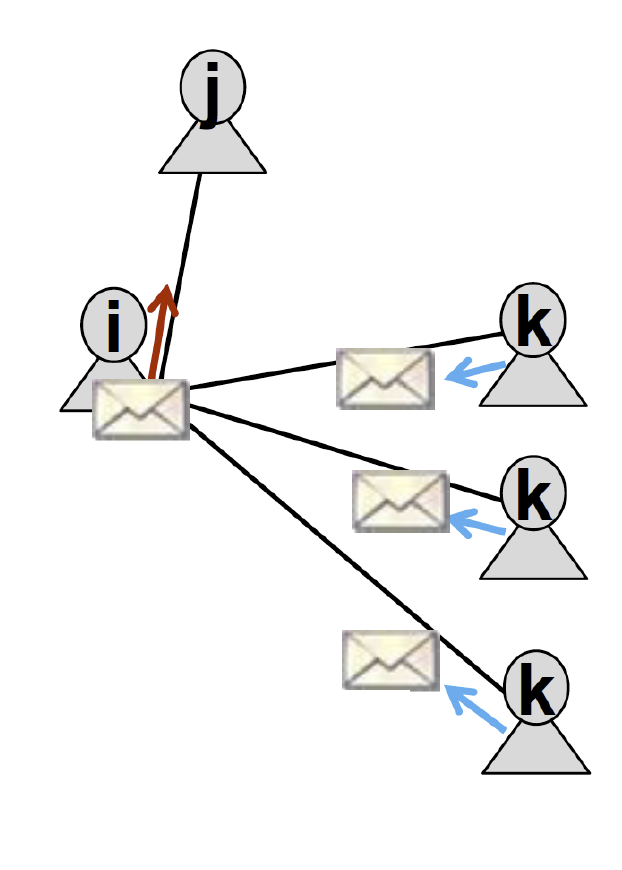
i는 j에게 message를 보낼 때, 주변 neighbor인 k에게 들은 내용을 전달합니다.
즉, neighbor k는 i에게 belief state를 전달합니다.
Notation
-
: Label-label Potential Matrix
- node와 neighbor 사이의 dependency
- : 노드 j의 neighbor i가 state 에 있을 때, 노드 j가 state 에 속할 확률
= correlation between node i & j
-
: Prior Belief
- : 노드 i가 state 에 속할 확률
- : j가 state 에 있을 때 i의 추정치
= i's message
-
: 모든 state의 집합
PROCESS
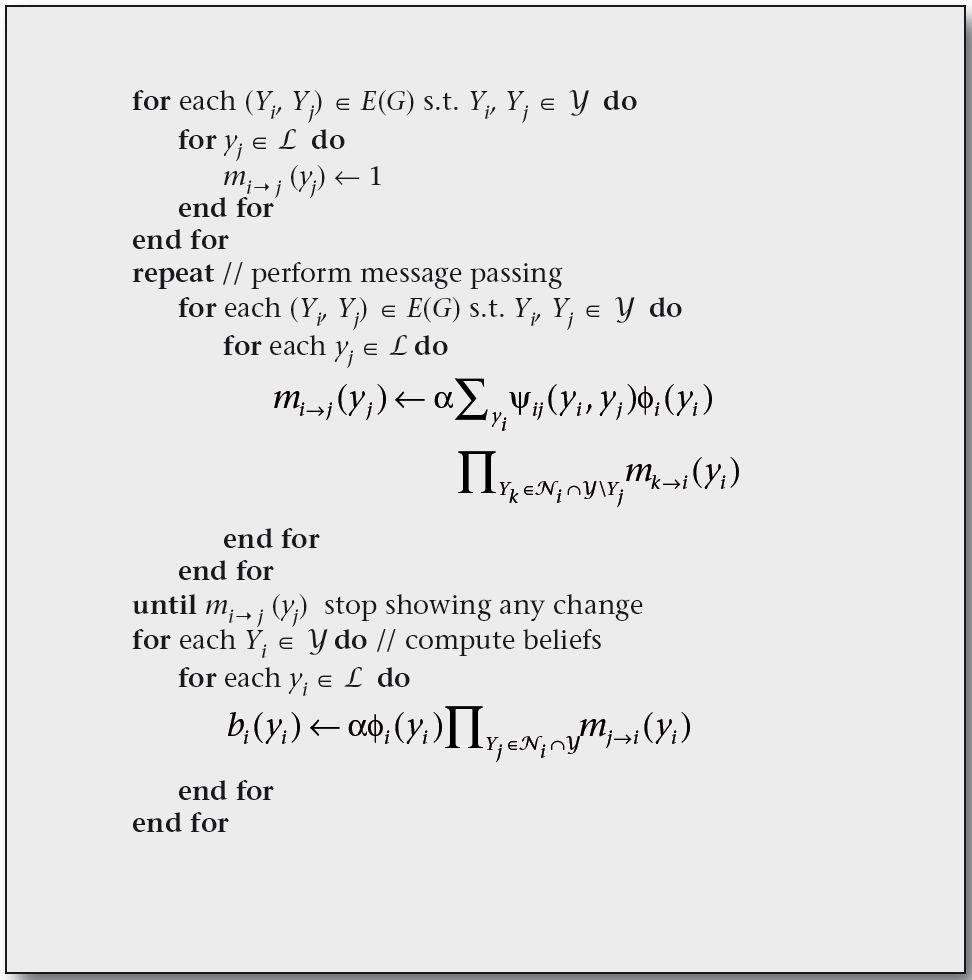
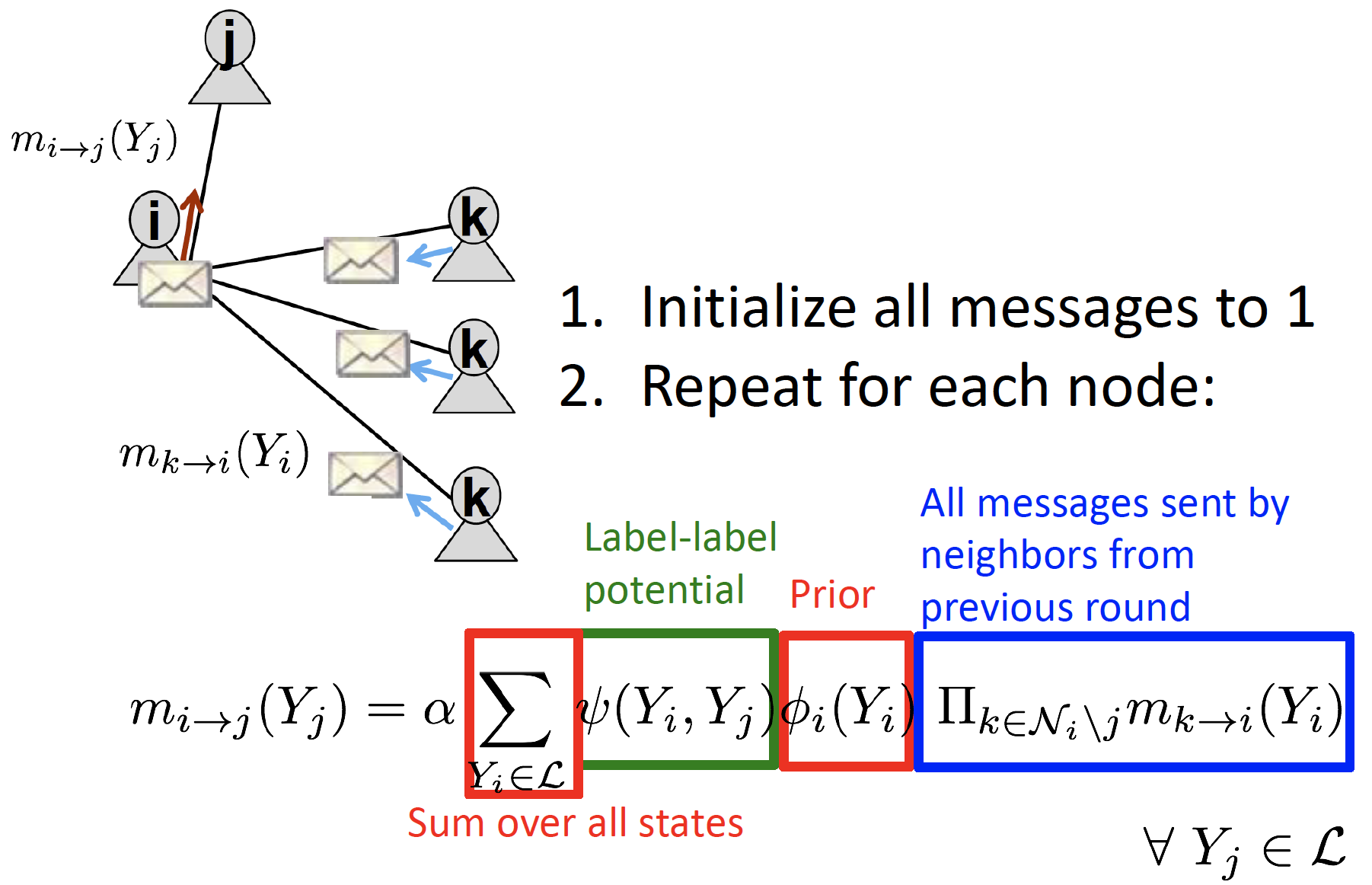
-
모든 message를 1로 초기화 한 후, 각 노드에 대해 다음을 반복합니다.
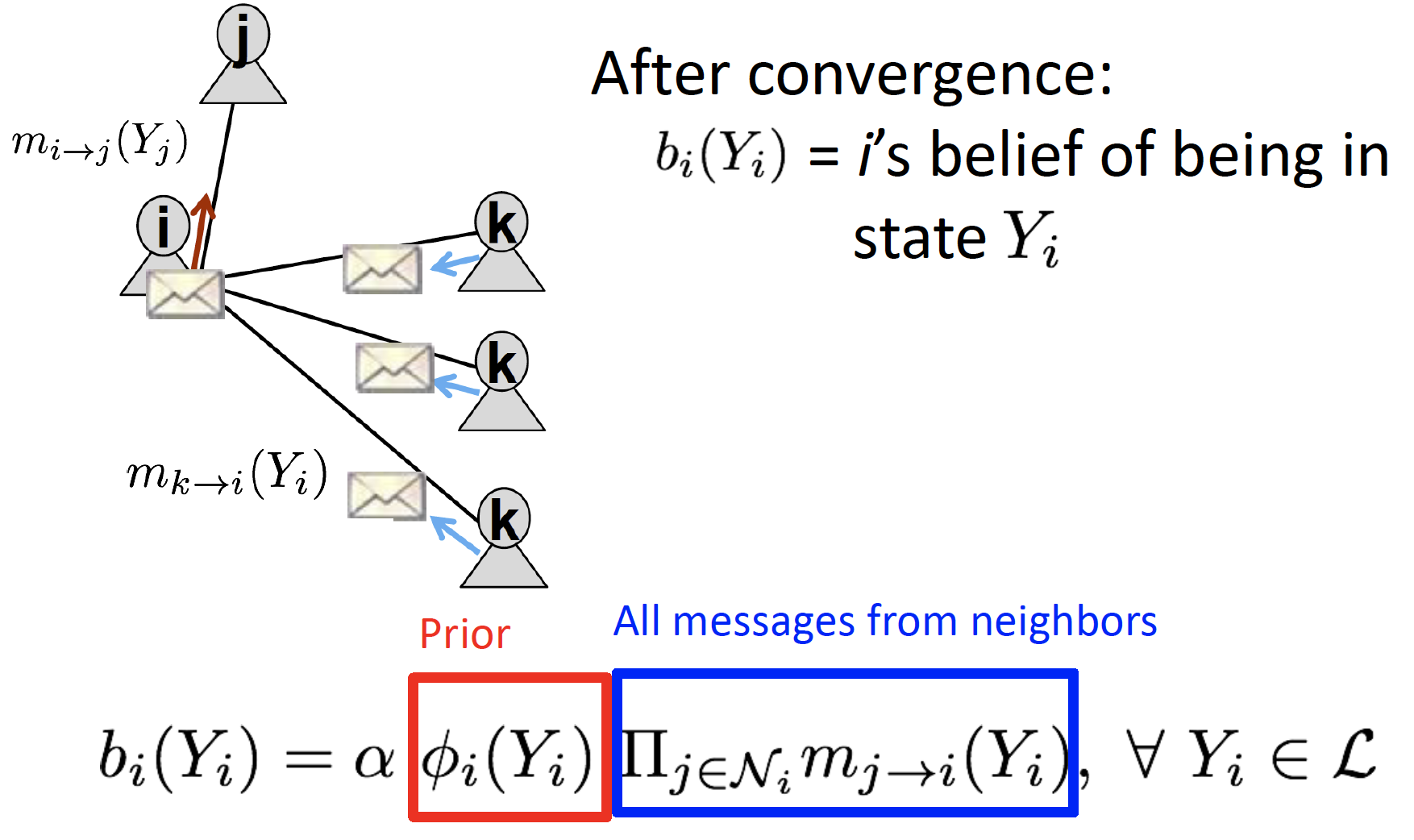
-
수렴하면, 각 state에 대한 belief 를 계산합니다.
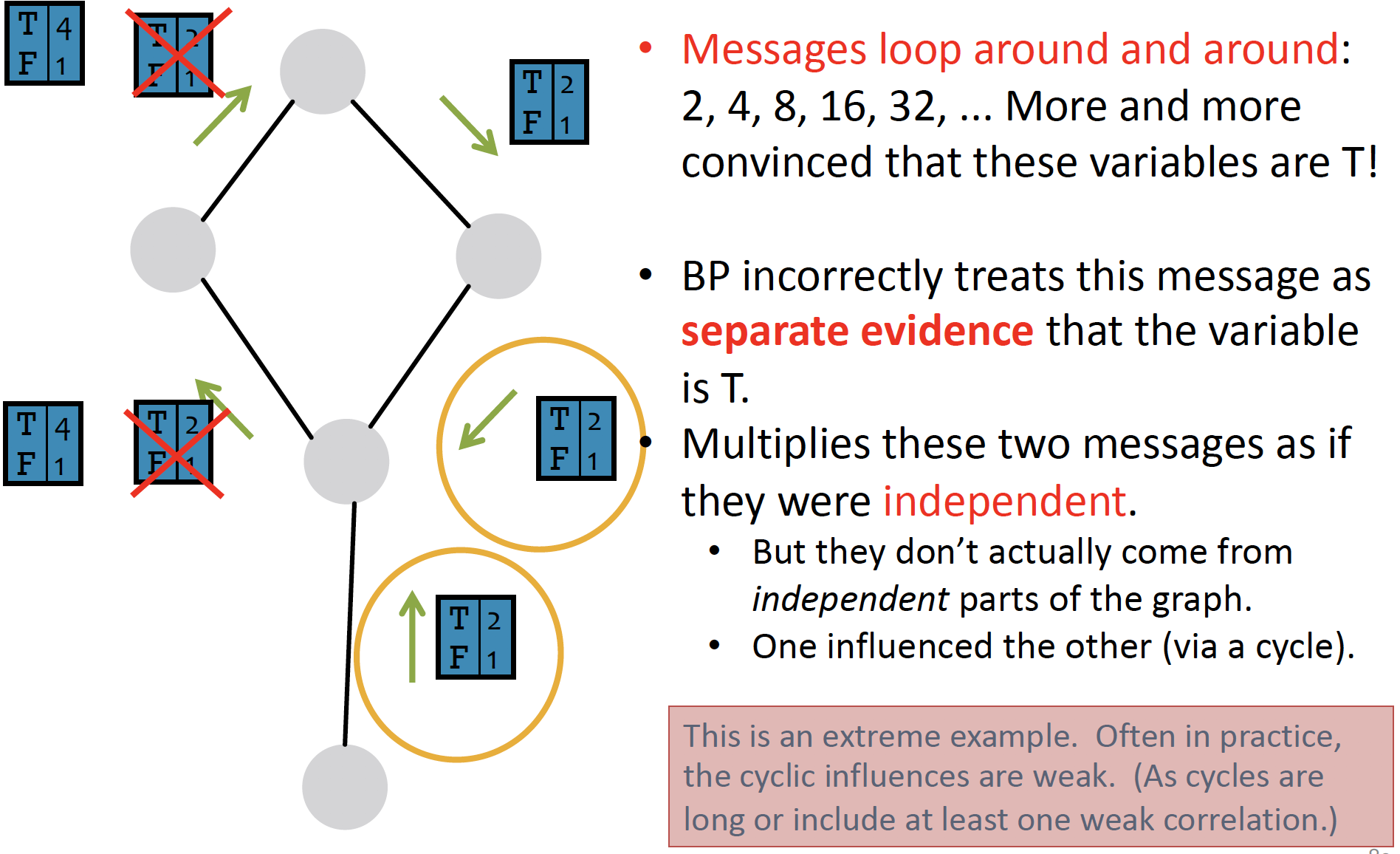
Loopy BF는 cyclic graph에서 사용할 수 없습니다. (no longer independent)
Summary
- Advantages
- 프로그래밍 및 병렬화가 쉽습니다.
- 어떤 그래프 모델보다도 general하게 적용 가능합니다. (+ higher order than pairwise)
- Challenges
- 수렴이 보장되지 않습니다.
- 특히 많은 closed loop가 있는 경우, 적용이 어렵습니다.
(Clustering Coef를 확인해 보고, Belief Propagation 적용 가능성을 검토해 볼 수 있습니다.)
- Potential Functions
- parameter 추정을 위해 train이 필요합니다.
- gradient-based 최적화가 진행됩니다.
NetProbe : Online Auction Fraud
Online Auction Fraud
- 경매 사이트는 사기 치기에 상당히 매력적인 장소입니다.
종종 상품 배달을 못 받았다는 사기를 치곤 하며, 이러한 사기 사건 하나 당 발생하는 평균 손실 비용이 $385 라고 합니다. - 단순 individual feature (user attributes, geographic locations, login times, session history, etc) 만으로 사기꾼을 탐지하기는 어렵습니다.
- 따라서
graph structure을 구성하여, user 사이의 relationship 을 캐치하여 사기꾼을 탐지하고자 합니다.
Role of Users
Main Question : How do fraudsters interact with other users and among each other?
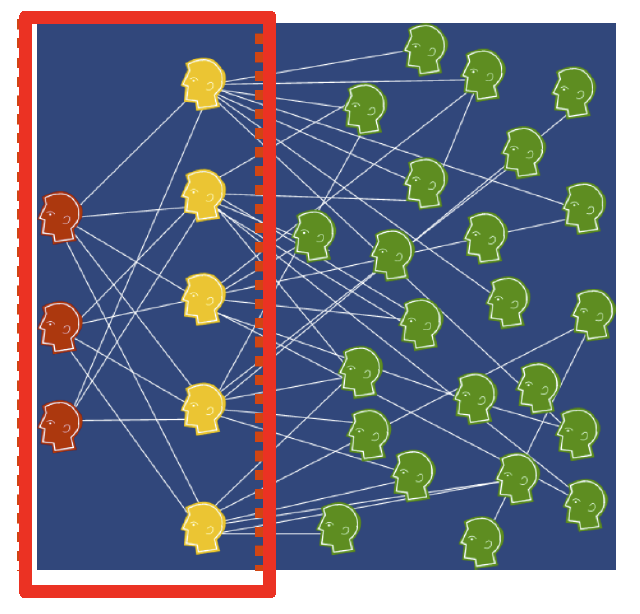
fraudster : 사기꾼 / accomplice : 공범 / honest : 선량한 시민들
- 경매 사이트에는 Reputation System 이 존재합니다.
- 사기꾼들끼리는 서로의 Reputation Score를 올려 주지 않는데, 한 명이 걸리게 되면 다 같이 걸리게 되기 때문입니다.
- 따라서 near-bipartite graph를 형성합니다.
- accomplice
- perfectly 하게 정상적인 것 처럼 보이는 user를 말하며, honest와 거래하며 high feedback rating 얻습니다.
- fraudster의 feedback rating 을 올려줍니다.
- fraudster
- accomplice 와 거래하며, honest 에게 사기를 칩니다.
- accomplice
- 사기를 치고 나면, fraudster는 사기 현장을 떠나고, accomplice는 사기 현장에 남아 다음 사기를 치는 것을 도와줍니다.
Detecting Auction Fraud
Markov Random Field & Belief Propagation

Propagation Matrix
: the likelihood of a node being in state given that it has a neighbor in state

- 해당 논문에서의 = 0.05 입니다.
- 즉, 노란색으로 칠한 값이 heavily linked 된 관계를 나타냅니다.
- Intuition
fraudster는 accomplice와 heavily link 되어 있으나, 다른 bad node와의 연결은 피하는 양상입니다.accomplice는 fraudster 와 honest 모두와 연결되어 있으며, 특히 fraudster와 더 잘 연결되어 있습니다.honest는 accomplice와 다른 honest와 연결되어 있습니다.
PROCESS
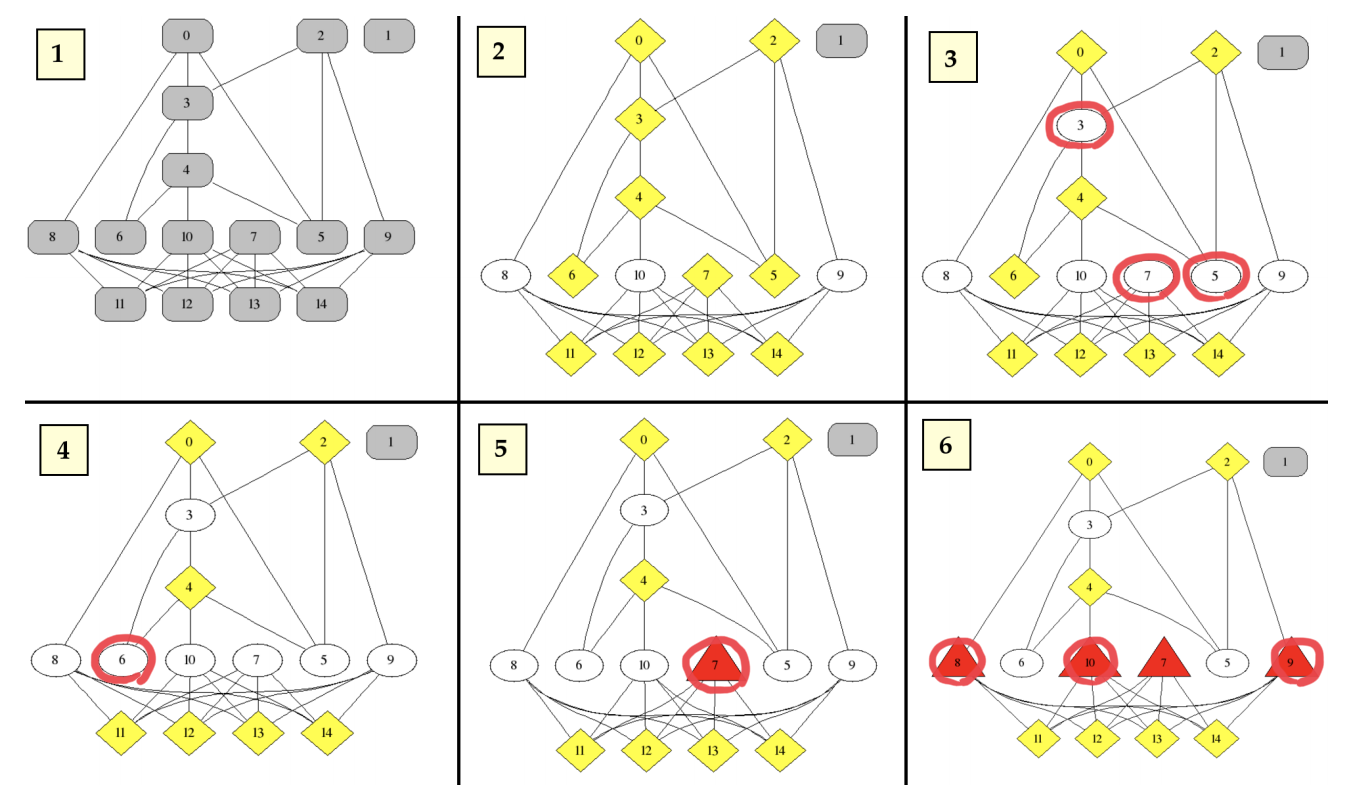
- fraudster, accomplice, honest 확률값을 모두 같게 initialize 합니다.
- 각각의 node는 iteratively 하게 message를 pass하며, belief를 update 합니다.
- 에 따르면, iteration 1 이후의 node는 accomplice 가 될 가능성이 높습니다. accomplice 로 분류된 node에 대해서, 이웃을 fraud 혹은 honest 로 두고, 값을 계속적으로 update 합니다.
- 수렴할 때 까지 update 합니다.
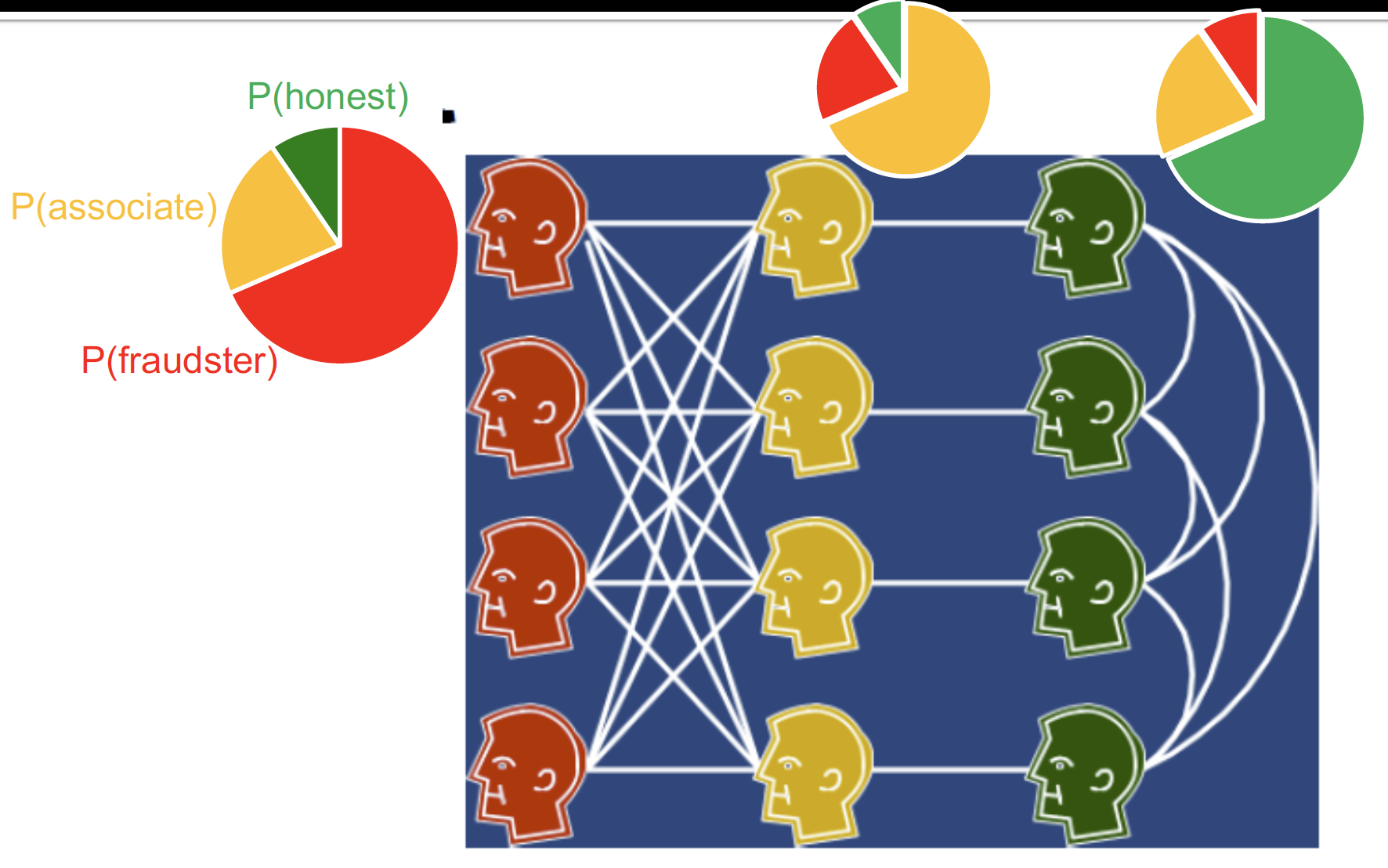
분류가 잘 된 것을 볼 수 있습니다.
Reference
- Tobigs Graph Study : Chapter 6. Message Passing and Node Classification
- 데이터 괴짜님 Review : CS224W - 06.Message Passing and Node Classification
- snap-stanford Review : Message Passing and Node Classification
- CS224W Winter 2021 : 5. Label Propagation for Node Classification
- REV2: Fraudulent User Prediction in Rating Platforms
- NetProbe : A Fast and Scalable System for Fraud Detection in Online Auction Networks
- Collective Classification in Network Data
3개의 댓글
Lecture 6 Message Passing and Node Classification 에서는 주어진 graph에서 노드에 부여된 기존 label를 기준으로 다른 unlabeled 노드에 label을 예측하는 Semi-supervised node classification에 대해 다룹니다.
semi-supervised learning이란 label 데이터와 un-labeled 데이터를 동시에 학습해서 보다 성능이 높은 모델을 구축하는 방법론입니다. 데이터가 군집의 형태를 따르고 있다면, 학습에 도움이 될 것이라고 재빈님께서 말씀해주셨습니다.
앞서 5강에서 다뤘듯이 주어진 graph에 군집이 있다고 가정했을 때, 이러한 semi-supervised learning을 통한다면 보다 효과적인 학습과 분류가 가능할 것이라 말합니다.
Collective classification란 네트워크의 모든 노드의 label를 할당하자는 과제를 의미합니다. 주어진 그래프 내에는 Correlations이 존재하기에 측정할 수 있기 때문입니다. collective classification을 위해서는 3가지 테크닉이 사용됩니다.
- Relational classification
- Iterative classification
- Belief propagation
상관관계라고 해석 가능한 Correlation가 그래프에서 존재하기 위해서는 3가지 dependency를 따릅니다.
- Homophily: 비슷한 성향/특성/역할을 지닌 사람들이 결속하는 경향을 의미
- Influence: 누군가의 성향/특성/역할이 social connections이 되어있는 다른 사람들에게 영향을 미침을 의미
- Confounding: 외부적인 요인이 개인 및 social connections에 영향을 미침을 의미
그렇다면 주어진 그래프에서 어떻게 correlation을 측정할까요. 해당 과정에는 markov assumption에 기반한 3가지 Step이 존재합니다.
(1) Local Classifier: node features/attributes를 기반으로 label를 예측합니다. 해당 과정에서는 network 정보를 사용하지 않습니다.
(2) Relational classifier: correlation을 capture하는 과정으로, 이웃 노드의 label과 attributes 정보를 활용하여 correlation을 얻고 classifier를 학습하는 것으로 이해했습니다.
(3) Collective Inference: 2 step에서 얻은 correlation을 전파하고 학습된 relational classifier를 노드에 반복적으로 적용하여 추론합니다.
Relational Classifier
un-labeled 노드의 label를 분류하기 위해서 이웃 노드의 class probability의 weighted average(가중 평균)을 사용하는 분류기를 말합니다. 이 때, labeled node는 ground-truth label로 초기화하고 un-labeled node의 경우 균등한 확률로 설정한다고 합니다.
하지만 해당 과정은 convergence를 보장하지 않으며 node feature를 사용하지 않는다는 단점이 있습니다.
Iterative classification
node features를 사용하지 못하는 Relational Classifier의 단점을 극복하기 위해 label 뿐만 아니라 node feature까지 고려할 수 있는 Iterative classification이 제안되었습니다. Iterative classification은 크게 2가지 phase의 과정을 가집니다.
- Bootstrap Phase
- : 각각의 node i에 대해ㅐ flat vector 를 생성합니다.
- : 를 local classifier(ex. SVM, KNN, LR)을 통해 분류합니다.
- aggregate neighbors: 다양한 집계 함수를 활용해서 이웃 노드의 정보를 집계합니다.
- Iteration Phase
- Repeat: 모든 node i에 대해 해당 과정을 반복합니다.
- Iterate: label이 stabilize되거나 최대 iteration을 만족할 때까지 반복합니다.
Belief Propagation
이웃 노드의 조건부확률을 적용해 interaction tree를 구축해 노드 간 상호작용 정보를 보다 활용한 방법으로 이해했습니다. 해당 방식을 Message Passing 매커니즘이라 하기도 합니다. 하지만 정확히 어떤 목적을 위한 방법인지는 이해하지 못한 것 같습니다. 아마 어떠한 분류기 자체를 의미하기 보다는 분류기에서 보다 정확한 분류를 위해 추가할 수 있는 어떠한 테크닉으로 이해했습니다.
이번 강의는 Graph의 한정된 node label로 unlabeled node를 classification할 수 있는 model에 대해 배웠습니다.
1. Relational Classification
idea : 의 class probability는 neighbor 노드들의 class probability의 weighted average
training :
- initialization : labeled node는 GT로 initialize하고, unlabeled node는 uniformlygkrp 0.5로 설정하거나, 신뢰할 만한 prior로 initialize합니다.
- training : '수렴할 때 까지' 또는 '최대 iteration 수에 도달하기까지' 모든 node i 와 label c에 대해 으로 random order로 업데이트.
한계 : 그래프의 크기가 커질수록 coverage가 보장되어 있지 않고, node feature를 전혀 사용하지 않습니다.
2. Iterative Classification
idea : node i의 attribute & neighborhood 의 label 모두 고려
training : 각가의 node 에 대해 flat vector 를 생성하고 SVM,KNN,KR등의 local classifier를 통해 분류합니다(). 그 후, count, mode, proportion, mean, exists 등의 neighborhood information 을 취합합니다. class label이 stabilize 되거나 최대 iteration 횟수가 만족될 때까지, node vector 를 update -> 에 대해 update를 반복합니다.
- : feature vector 만으로 node label 을 예측하는 classifier
- : feature vector 와 의 nieghborhood 를 모두 이용하여 label 을 예측하는 classifier
한계 : coverage가 보장되지 않습니다.
3. Belief Propagation
idea : message passing. dynamic programming 접근 방식으로, graph model에서 조건부 확률로 답을 구하는 방식
message passing:graph 에서 node의 개수 세는 알고리즘으로, 각 node들은 그들의 neighbors와만 interact 할 수 있습니다. 각 node들은 그들의 neighbor로 부터 message(각 노드의 이웃의 수를 전달->합->전달)를 전달받고, 이를 update 하여, 앞으로 전달합니다. 각 node들이 서로 전달전달 하는 정보를passing a belief라고 하고, 이를 토대로belief propagation을 내리게 됩니다. (grpah가 cycle한 경우에는 잘 동작하지 않습니다.)
training : 모든 message를 1로 초기화 한 후, 각 node에 대해 반복합니다. 수렴하면, 각 state에 대한 belief
장점 : 프로그래밍 및 병렬화가 쉽고, 어떤 그래프 모델보다 general하게 적용 가능합니다.
한계 : message passing을 이용하기 때문에 cycle이 있는 경우, closed loop에서는 사용하기에 한계가 있습니다. 수렴이 보장되지 않습니다.
꼼꼼하게 강의해주신 S2이재빈S2님 감사드립니다.



이번 강의에서는 message passing과 graph를 이용한 machine learning task에 대하여 배웠습니다.
가장 대표적 task인 classification을 보면 graph에서는 주어진 label을 이용하여 unlabeled node를 예측하는 일을 진행할 수 있습니다. 이 때 homophily한 경우 즉, 비슷한 node끼리는 연결되어 있다는 가정하는 것이 collective classification입니다. classification을 위해서는 마르코프 가정을 사용합니다. 이는 rnn처럼 현재 상태는 이전 상태에 의해서 결정된다는 가정인데, graph에서도 직접 연결되어있는 이웃 node에 의하여 현재 node의 상태를 알 수 있다는 것이죠. 과정은 다음과 같습니다. (1) 초기 label을 부여하고 node feature만으로 basic한 classification task를 진행합니다 (2) classifier가 이웃 node feature를 학습합니다 (3) 이 과정을 모든 노드마다 결과가 수렴할때까지 반복합니다. 이때, propagete되는 정보는 최초 initial이 아닌 매 학습마다 업데이트 되는 정보이기 때문에 사실상 iteration이 진행될 수록 network의 전체 정보를 사용할 수 있다고 볼 수 있습니다. 이웃 node feature를 학습하는 relational classification에 대하여 살펴보면 현재 node의 label은 이웃 node의 label probability의 weighted average라는 가정이 들어갑니다. 따라서 모든 노드에 대하여 어느정도 수렴할 때까지 반복해서 학습하면됩니다. 그러나 무조건 수렴이 보장되지 않고, node feature를 사용하지 않는다는 한계점이 있습니다. 반대로 node feature까지 고려할 수 있는 interative classification이 있습니다. 이 방법은 2가지 phase로 구분되어 학습됩니다. 첫째 bootstrap phase에서는 node feature를 활용한 local classifier를 학습하고 iteration phase에서는 local classifier로 이웃 node를 예측하면서 이들의 정보까지 학습하는 단계를 거칩니다. 또 다른 classification 사례로 REV2의 fake review detection이 있습니다. 단순한 review 정보로 분류하기 어려운 task에서 graph structure에서 relationship 정보를 활용합니다. black consumer는 좋은 상품에 낮은 평점을, 광고하기 위한 상품에는 좋은 평점을 주면서 일반적인 소비자와 다른 행동을 보입니다. 이에 fairness, reliability, goodness 3가지 score를 학습하여 fairness가 유독 낮은 사람을 찾아냅니다. 이 방법은 수렴이 보장되어 있으며 시간복잡도는 edge수에 따라 O(n)이고 laplace smoothing으로 cold start problem을 어느정도 잡아낼 수 있다고합니다.
graph에서 node의 개수를 세는 task를 진행한다고 할 때 단순히 node를 순차적으로 타고 넘어가면서 개수를 셀 수 있습니다. 그러나 이 방법은 cycle을 이루는 graph에서는 통하지 않습니다. loopy belief propagation를 살펴보면 (1) 모든 message를 1로 초기화 한 후, 각 노드에 대해 다음을 반복하고 (2) 수렴하면 각 state에 대한 belief를 계산합니다. 이러한 방법은 프로그래밍 및 병렬화가 쉽고 general하게 적용 가능하다는 장점이 있습니다. 그러나 무조건 수렴이 보장되지 않고 특히 closed loop의 경우 적용하기 어렵숩니다. message passing을 활용한 classification 사례로 NetProbe가 있습니다. fraudster를 잡아내는 task로, 이들은 accomplice와 정상적인 허위 거래를 통해 평판을 만들고 목표 고객에게 사기를 치는 패턴을 보입니다. 이러한 양상을 propagation matrix로 정의하고 markov random field와 belief propagation을 활용하여 학습을 진행하면 됩니다. 강의에 빠진 부분도 찾아서 넣어주신 배려가 좋았습니다. 좋은 강의 준비해주셔서 감사합니다.