Lecture 4 - Backpropagation and Computation Graphs

작성자 : 세종대학교 응용통계학과 조준혁
1. Derivative wrt a weight matrix
1) Chain Rule?
chain rule은 연쇄법칙으로 합성함수의 미분법을 의미합니다.
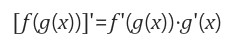
Neural Network에서는 이러한 합성함수의 미분법인 chain rule을 이용하여 최종 scalar 값을 weight로 미분해가며 가중치를 업데이트 하는 방식으로 학습이 진행됩니다.
2. Deriving gradients: Tips
1) Carefully define your variables and keep track of their dimensionality!
* (변수를 잘 정의하고 차원을 계속 숙지할 것)
2) Chain rule! - Keep straight what variables feed into what computations
* (연쇄법칙을 잘 알고 사용할 것)
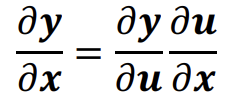
3) For the top softmax part of a model
First consider the derivative wrt (softmax) when (the correct class)
Then, consider derivative wrt (softmax) when (all the incorrect classes)
* (마지막 softmax 값에 대해 correct class / incorrect class를 따로따로 미분해줄 것)
4) Work out element-wise partial derivatives if you're getting confused by matrix calculus!
* (행렬 미분 방법이 헷갈린다면 성분별 부분 미분을 연습할 것)
5) Use Shape Convention.
The error message that arrives at a hidden layer has the same dimensionality as that hidden layer
* (Shape Convention을 이용하자. hidden layer에 도착하는 error 메세지 는 그 은닉층의 차원과 같다.)
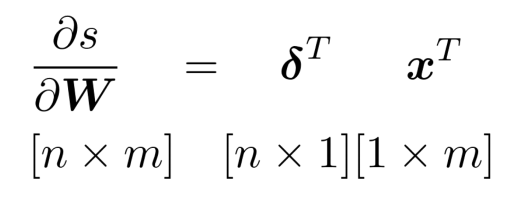
3. Deriving gradients wrt words for window model
지금까지 앞서 x와 W의 선형결합으로 이루어진 matrix에 대한 미분값을 살펴보았는데, Word들에 대해서는 어떻게 미분이 적용될지 알아보겠습니다.
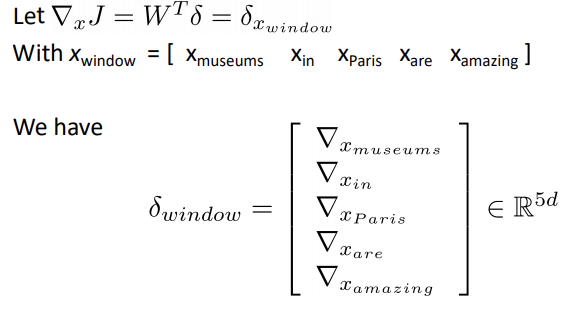
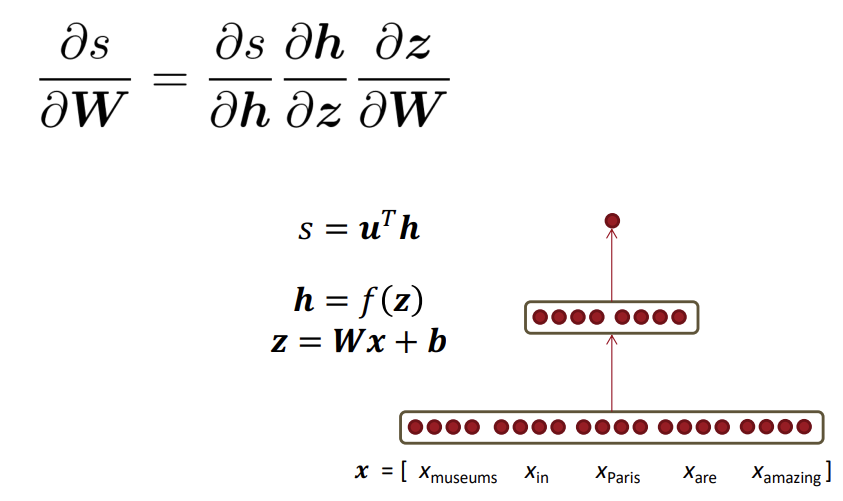
NLP는 말 그대로 "언어"를 입력받아 특정 task를 수행하게 됩니다. 이때 각각의 word들은 고유의 vector 값을 가지게 되는데, 이 벡터들을 결합한 행렬 전체를 task를 수행하기 위한 input으로 넘겨주는것이 아닌 window 단위로 넘겨주게 됩니다. 위에서 제시된 예시는 5개의 단어가 있고 각 단어는 d차원의 벡터입니다. 따라서 5xd 차원의 word window vector이며 window 단위로 가중치를 업데이트 하며 각 단어 벡터들이 task에 도움이 되는 방향으로 업데이트를 진행합니다.
4. A pitfall when retraining word vectors
하지만 위와 같은 방법으로 특정 task를 위해 word vector를 학습시키고 노드의 가중치와 워드 벡터를 업데이트 시키는 것이 항상 좋은 결과를 야기하는 것은 아닙니다.
다음의 예시를 살펴보겠습니다.
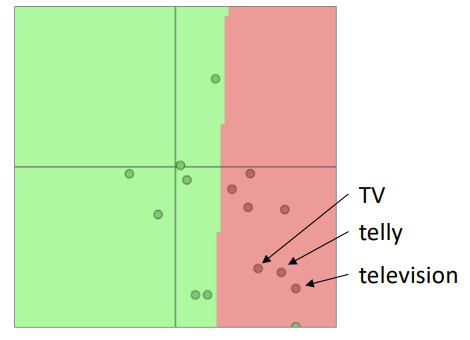
TV, telly, television 는 기본적인 의미가 같기 때문에 glove 등을 통해 워드 임베딩을 한다면 vector space 상의 세 단어는 매우 가깝게 위치할 것입니다.
하지만 만약 학습시키고자 하는 데이터셋에 TV, telly가 있고 television은 없다고 가정해보겠습니다.
학습 데이터를 이용해 모델을 학습시킨다면 TV와 telly는 모델의 목적(ex. movie review sentiment classification)에 맞게 가중치를 업데이트하며 움직이게 됩니다.
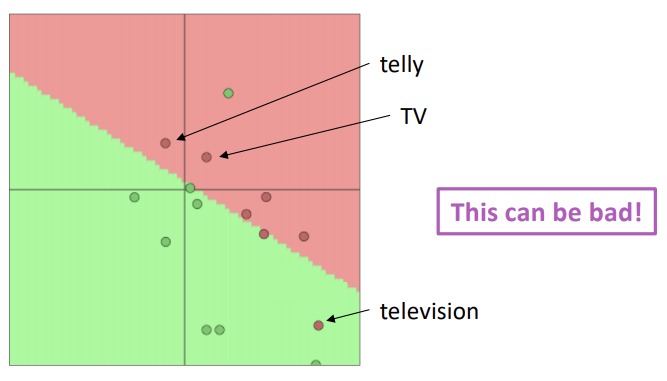
하지만 television의 경우에는 어떻게 될까요?
TV와 telly와 비슷한 의미를 지님에도 학습 데이터 셋에 포함되지 않는다는 이유로 가중치가 업데이트 되지 못해 모델로 하여금 다른 의미를 지닌 단어로 분류되게 됩니다.
Q. 이러한 부분은 어떻게 해결할 수 있나요?
A. 대부분의 경우 Pre-trained된 모델을 사용하면 됩니다.
Pre-trained 모델이란?
- 사전에 학습된 모델로 내가 풀고자 하는 문제와 비슷하면서 규모가 큰 데이터셋에 이미 학습이 되어있는 모델입니다.
지난 강의에서 소개되었던 Word2Vec, Glove 모두 Pre-trained 모델입니다.
Pre-trained 모델의 경우 이미 방대한 양의 데이터에 대해 학습을 마친 상태이므로, 위와 같이 TV, telly, television과 같이 비슷한 단어의 경우 훈련 데이터 셋 포함 유무에 관계없이 일정 수준의 유사 관계가 형성이 됩니다.
하지만 데이터의 양이 100만개 이상이라면(거의 불가능), 랜덤 워드 벡터로부터 시작해서 모델을 학습시켜도 괜찮습니다.
Q. Fine Tuning을 해야하나요?
A. 가지고 있는 데이터 셋의 규모에 따라 달라집니다.
Fine Tuning 이란?
- 기존에 학습되어져 있는 모델을 기반으로 모델의 구조를 목적 task에 맞게 변형하고 이미 학습된 weight로 부터 학습을 업데이트 하는 방법
1. Training dataset이 적은 경우(< 100 thousands)
- 그냥 사전 학습된 word vector를 사용할 것(fine-tuning 하지 않기)
2. Training Dataset이 많은 경우(> 1 million)
- word vector를 학습시키는 것이 성능이 좋아질 것(fine-tuning 하기)
5. Computation Graphs and Backpropagation
1) Computation Graph?
Computation Graph이란 "계산 그래프"를 의미합니다. 계산 그래프란 말 그대로 계산 과정을 그래프로 나타낸 것입니다. 그래프는 여러개의 node와 그 노드를 잇는 선(edge)로 표현이 됩니다.
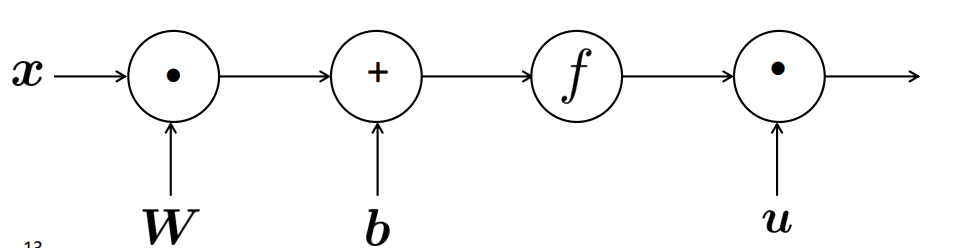
2) Forward Propagation(순전파)
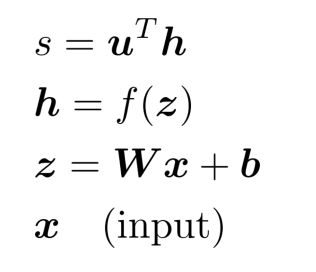
위의 수식을 얻기위해 계산 그래프의 왼쪽부터 차례대로 연산을 해나가 결괏값을 얻는 것을 Forward Propagation이라고 합니다.
3) Back Propagation(역전파)
Neural Network는 Forward Propagation을 통해 얻어진 결과와 실제값을 비교해 계산된 오차를 미분하며 가중치를 업데이트하는 방식으로 학습이 진행됩니다.
3-1) Single Node(Single Input)
이해를 돕기위해 먼저 하나의 input과 하나의 output으로 이루어진 계산 그래프를 생각해보겠습니다.
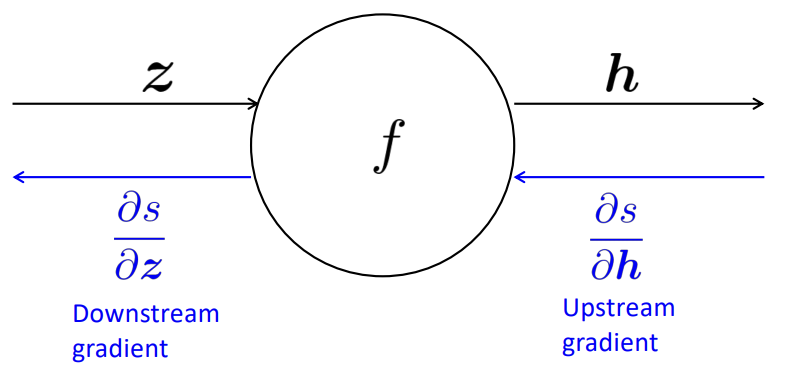
Back propagation의 진행 방향을 생각해볼 때 Upstream gradient와 Downstream gradient의 순서로 미분값을 계산하게 됩니다.
하지만 Downstream gradient를 수행할 때 s는 z로 이루어지지 않아 적절히 미분을 수행할 수 없습니다.
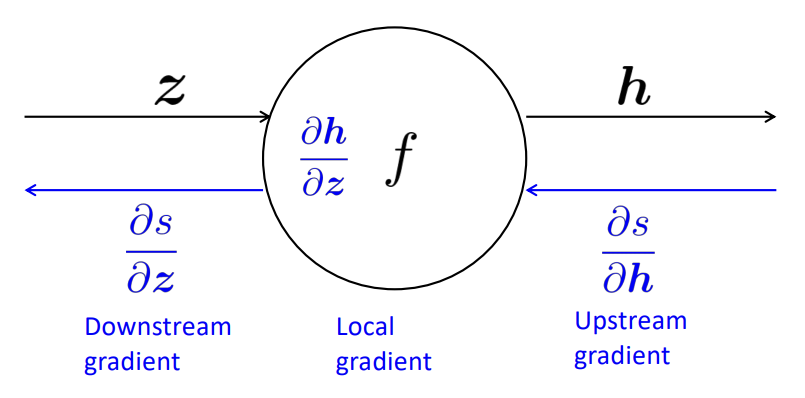
이를 해결하기 위해 Forward Propagation 수행 시의 output을 input으로 미분한 Local gradient를 이용해 Downstream gradient를 계산할 수 있게 됩니다.
결론적으로는 Chain Rule을 이용한 것과 같은 결과입니다.
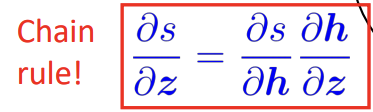
3-2) Single Node(Multiple Input)
조금 더 일반화를 하기 위해 더 많은 Input이 있을 경우에는 어떻게 Back Propagation을 살펴보겠습니다.
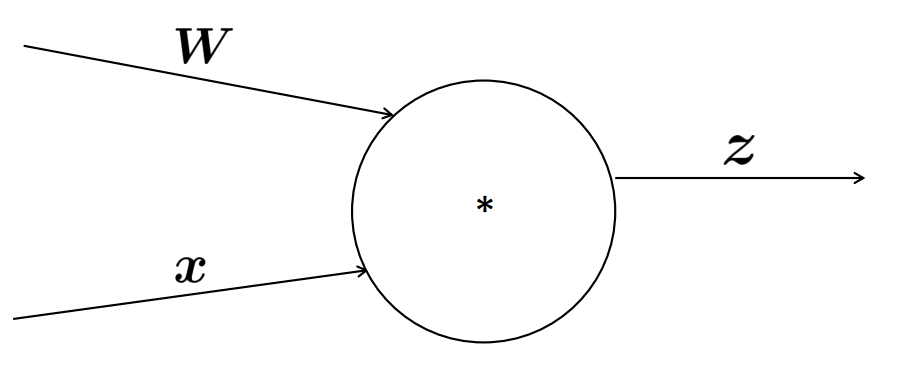
간단히 말하면 위에서 소개해드린 방법을 여러번 수행한다고 생각하시면 됩니다.
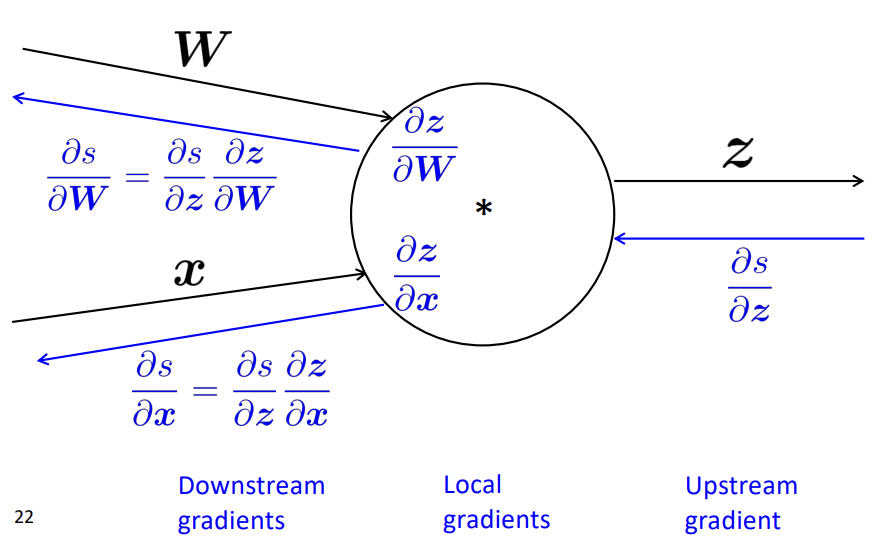
동일하게 Upstream gradient에 각각의 Input에 대한 Local gradient를 계산해 곱해주어 각 Input에 대한 미분을 수행하며 Back Propagation을 수행합니다.
3-3) Efficiency
다음은 계산 그래프를 통해 back propagation을 수행할 때 효율적으로 미분값을 얻는 방법을 소개하겠습니다.
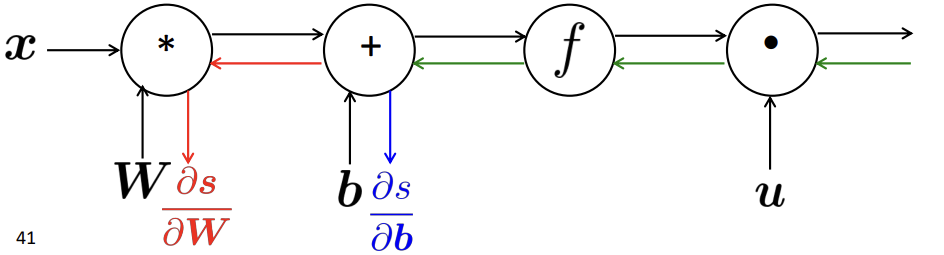
방법은 간단합니다.
미분을 계산할 때 한번에 다 계산을 하라는 것입니다.
각 노드의 미분 계산 값을 잘 가지고 있다가 원하는 값을 계산하고자 할 때 간단히 chain rule을 설계해 값을 대입하며 빠르게 값을 얻을 수 있을것 입니다.
(값을 저장해 추후에 local gradient 등을 다시 계산하지 않는다.)
3-4) Back propagation in General Computation Graph
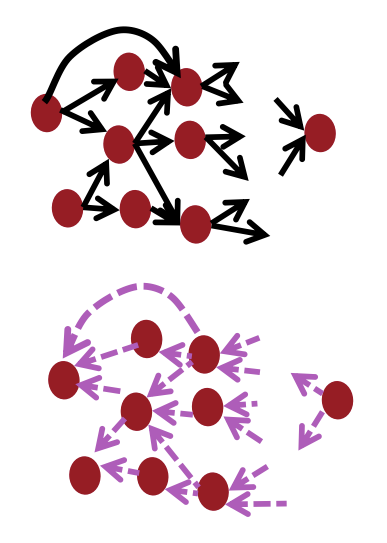
Compuation Graph의 일반적인 모습입니다.
위의 검정색 화살표 색깔로 Forward Propagation(순전파)가 진행되고 순전파가 진행된 최종 값을 바탕으로 보라색 선 방향으로 오류를 전파하며 값을 업데이트 해가는 Back propagation(역전파) 과정을 보여줍니다.
3-5) big O() complexity
순전파의 계산량을 생각해보면 각각의 Input들이 노드를 타고 연산을 거치며 최종 Scalar값까지 관여하게 됩니다.
역전파의 경우도 마찬가지로 Scalar 값으로 부터 순전파시 거쳐 지나갔던 노드를 지나며 Gradient를 구하게 됩니다. 이때, 앞선 3-3) efficiency 부분처럼 Local Gradient 등의 연산을 잘 저장해두었다가 필요시에 활용하게 되므로 추가적인 연산이 필요가 없게됩니다.
따라서, 순전파와 역전파의 시간복잡도는 동일하게 됩니다.
3-6) Gradient checking: Numeric Gradient
Pytorch나 Tensorflow 등의 딥러닝 프레임워크가 잘 발달되기 이전 딥러닝 초기의 데이터 과학자들은 Neural Network의 학습을 위해 직접 손으로 Gradient를 계산하며 Weight를 업데이트 하는 방식으로 학습을 진행했습니다.
정확한 Gradient 계산은 성공적인 네트워크 학습의 핵심이었으며 Gradient를 잘 계산했는지 여부를 엄격하게 체크했다고 합니다.
Gradient를 계산하는 방법에는 2가지가 존재합니다.
- Analytic Gradient(해석적 방법)
- Numerical Gradient(수치적 방법)
1번의 Analytic Gradient 방법은 이 강의의 주된 내용인 계산 그래프를 통한 연산시 활용되는 Chain Rule을 이용하여 Gradient를 계산하는 방식입니다.
Numerical Gradient 방식에 대해 소개해드리겠습니다.
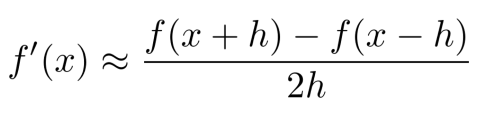
수치적인 방법은 해당 파라미터의 미분을 구하기 위해 미분의 공식을 이용해 계산을 하는 방법입니다.
다른 강의이지만 CS231N(2017) 강의에서 제시된 예시를 살펴보겠습니다.

현재 위와 같은 Weight를 가지고 계산된 Loss가 주어졌습니다.

첫번째 Weight에 대해서 굉장히 작고 0에 가까운 값을 더해 살짝 이동시켜보니 Loss가 감소했음을 알 수 있습니다.

이 Loss를 바탕으로 미분값을 계산합니다.

다음 Weight를 h만큼 이동시킨 Loss가 증가했습니다.

마찬가지로 Loss 값을 이용해 gradient를 계산해주게 됩니다.
위와같은 방식을 거치며 Gradient를 계산하는 방법을 Numerical Gradient 라고 합니다.
Numerical Gradient는 쉽게 미분값을 얻을 수 있다는 장점이 있지만 하나의 gradient를 계산하기 위해서 f의 값을 계속해서 계산을 해주어야 해서 연산량이 매우 많다는 단점이 존재합니다.
반면 우리가 주로 사용하는 Chain Rule을 이용한 Analytic Gradient 계산 방법은 정확하고 빠르지만 계산 과정에서 실수가 있을 수 있다는 단점이 존재합니다.
이러한 단점을 보완하기 위해, 특정 Weight에 대한 미분이 잘 계산이 되었는가를 확인하기 위한 방법으로 Numerical Gradient 방법을 통해 미분을 계산해보는 Numeric Gradient Check 방식을 활용합니다.
6. Tips and Tricks for Neural Networks
1) Regularization
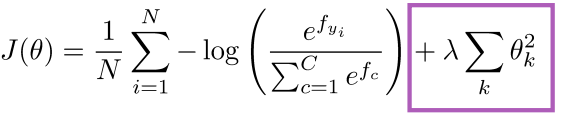
학습시키는 모델은 굉장히 많은 파라미터들을 가지고 있습니다.
손실함수만을 이용해 모델을 학습시키게 된다면, 모델이 학습 데이터는 잘 적합시키지만 테스트 데이터 셋은 잘 적합시키지 못하는 Overfitting(과적합)을 야기할 수 있습니다.
따라서 를 감소시켜야 하는 손실함수에 를 증가시키는 규제항을 추가하며 과적합을 방지할 수 있습니다.
주로 R2 규제항을 많이 사용하며 feature 들이 많을수록 효과적이라고 합니다.
2) Vectorization

word vector들을 각각 돌며 Weight matrix와 행렬곱을 수행할때의 시간과 word vector들을 하나의 matrix로 합친 뒤 W와 곱연산을 했을때의 시간 차이는 10배 이상 납니다.
따라서 반복문을 사용하기보다는 matrix 연산을 사용하는것이 학습의 시간을 감소시키는데 효과적일것 입니다.
3) Non-Linearities
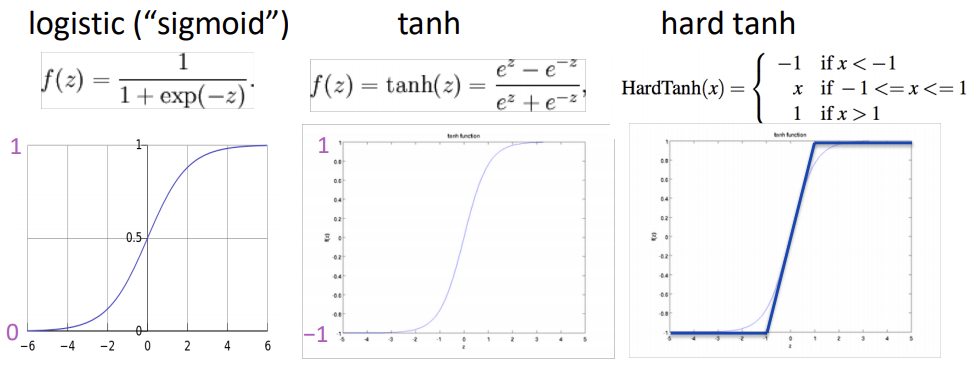
딥러닝 초기의 비선형 활성함수로는 logistic, tanh 함수가 자주 사용되었습니다.
하지만 두 함수 모두 exponential(지수) 연산이 필요해 연산량이 많아 Deep Learning에는 적합하지 않습니다.
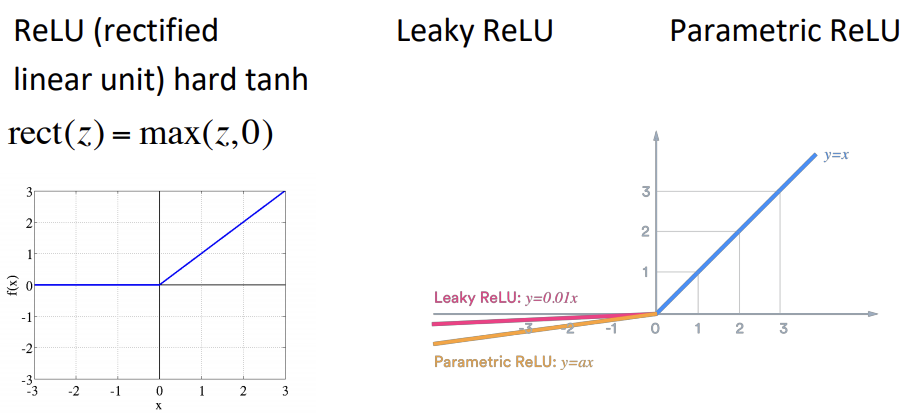
딥러닝을 설계할때 가장 먼저 고려해야할 비선형 함수는 좌측의 ReLU입니다.
ReLU는 가장 간단한 비선형 함수이면서도 좋은 성능을 자랑합니다.
ReLU는 음수값에 대한 Gradient를 0으로 취급하기 때문에 이를 보완하고자 Leaky ReLU, Parametric ReLU 등의 ReLU가 변형된 비선형 함수가 제안되고 있습니다.
4) Parameter Initialization
- Weight를 Small Random Value로 초기화 해야한다.
- Hidden Layer & Output의 Bias들은 0으로 초기화한다.(실제 Weight가 0이었을때 최적의 값을 얻기 위함)
- 다른 Weight들은 너무 크지도, 작지도 않은 범위 내의 Uniform distribution에서 임의로 추출한다.
- 이전 layer의 크기와 다음 layer의 크기를 고려해 가중치의 분산을 조절해주는 Xavier Initialization 방법도 많이 사용된다.
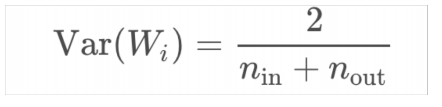
5) Optimizers
보통의 경우 일반 SGD를 사용해도 좋은 결과 성능을 예상할 수 있습니다.
하지만 더 좋은 결과를 기대한다면 learning-rate를 적절히 조절해주는것이 필요합니다.
더 복잡한 신경망일 설계할 때는 "Adaptive" Optimizers를 사용하는 것이 더 좋습니다.
Adaptive Optimizer는 계산된 Gradient에 대한 정보를 축적하며 파라미터를 조절해가는 방식을 사용합니다.
ex) Adagrad, RMSprop, Adam, SparseAdam...
6) Learning Rates
0.001 정도의 Learning Rate로 학습을 진행할 수 있습니다.
Learning Rate가 너무 클때는 모델이 발산할 가능성이 있고 너무 작으면 업데이트양이 작아 학습을 느리게 합니다.
대부분의 경우 학습을 진행시키며 learning rate를 감소시키는것이 성능 향상에 도움이 됩니다.
7. Reference
- https://www.youtube.com/watch?v=yLYHDSv-288
- https://web.stanford.edu/class/archive/cs/cs224n/cs224n.1194/slides/cs224n-2019-lecture04-backprop.pdf
- https://22-22.tistory.com/17
- https://wikidocs.net/91065
- https://winixsite.wordpress.com/category/ai-ml-dl/
- https://velog.io/@tobigs-text1314/CS224n-Lecture-4-Backpropagation-and-Computation-Graph
12개의 댓글
투빅스 14기 정세영
backpropagation의 기초적인 내용을 다시 잘 짚을 수 있었고, NLP와 연결하여 이해할 수 있었습니다.
- softmax 값에 대해 correct class와 incorrect class가 미분 식이 다르다.
- NLP에서는 학습할 때 window 단위로 input을 넘겨주어 가중치를 업데이트한다.
- pre-trained 모델을 사용할 때 일반적으로 일정 수준(십만 개) 이하라면 fine tuning을 권장하지 않는다. (안하느니만 못하다.)
- computation graph 측면에서 보면 순전파나 역전파나 scalar 값에서부터 동일한 노드들을 지나며 gradient를 구하게 되므로 시간 복잡도가 동일하다.
투빅스 14기 강재영
Backpropagation과 NLP retraining에 관한 전반적인 내용을 학습할 수 있었습니다.
-
A pitfall when retraining word vectors
- 특정 Task를 위해 word vector를 학습시키고 노드의 가중치와 워드 벡터를 업데이트하는게 항상 좋은 결과를 야기하지 않음
- 대부분 Pre-trained된 모델을 사용하며, 새로 학습시킬 경우 단어간의 관계가 잘 임베딩되지 않음
- 데이터가 1 millon 이상 존재한다면 추가적으로 Fine tunning을 고려
-
Computation Graphs and Backpropagation
- DownstreamGradient = LocalGradient * UpstreamGradient
- 각 노드의 미분계산 값은 저장해두어 원하는 값을 계산할 때 바로바로 사용
-
Regularization : 과적합 방지 방법 / Vetorization : 연산시간 감소 방법 / Actiovation : Relu, tanh 등 다양한 비선형 함수 ( 실제 많은 현실의 문제들은 비선형 문제이기 떄문에 ) / Parameter Initialization : Small Random Value / Uniform disribution( 너무 크고, 너무 작지 않게 적당한 값 배분 ) / Xavier ( 이전 레이어와 다음 레어이의 크기를 고려해 가중치의 분산을 조절 )
투빅스 15기 이수민
- 수행할 task에 맞추어 가중치 업데이트를 진행하고 word vector를 학습시켜 업데이트하는 것은 오히려 잘못된 결과를 낼 수 있기 때문에, pre-trained 모델을 사용하는 것을 추천한다.
- 가지고 있는 데이터가 100만 개 이상일 때는 fine-tuning을 진행하는 것이 성능 향상에 도움이 되지만, 그렇지 않다면 하지 않는 것이 좋다.
- Computation graph는 값을 그래프 노드 위에 위치시킨다는 것. 그래프 기반의 연산을 진행함으로써 효율적인 연산이 가능해진다.
- Numeric gradient를 통해 gradient를 잘 구했는지 확인할 수 있지만, 이 방법을 사용하면 계산량이 너무 많아지기 때문에 딥러닝에 직접적으로 활용하기 어렵다.
- Backpropagation의 문제점인 vanishing gradient / dying ReLU / overfitting을 방지하기 위해 regularization, vectorization, ReLU의 다양한 variation 고려, 가중치 초기화 (gradient vanishing 방지), optimizer 사용, learning rate 설정 등과 같은 방법이 사용된다.
투빅스 14기 이정은
- 특정 task를 위해 가중치와 word vector를 업데이트 시키는 과정이 항상 좋은 결과물을 내지는 않습니다. 이런 경우에는 pre-trained된 모델을 사용함으로서 해결이 가능합니다. Fine-tuning은 자신이 가지고 있는 데이터 사이즈에 따라 정하면 되며, 적은 경우는 굳이 할 필요가 없습니다.
- Backpropagation은 Downstream gradient = Local gradient * Upstream gradient로 계산이 이루어지며, 계산한 미분 값을 저장하면 해당 동작을 반복하지 않고 효과적인 연산이 가능합니다.
- Numerical gradient는 수를 아주 조금 변화시켰을 때의 loss의 변화값으로 미분을 계산하는 것으로 연산량이 많지만 정확한 값을 가집니다. 이는 Chain Rule로 연산한 미분 과정을 확인하는 데에 사용될 수 있습니다.
- Neural Network는 Regularization, Vectorization, Non-Linearities(ReLU, Leaky ReLU), Parameter Initialization(Xaiver), Optimizer(Adam, ...), Learning rate 조정 등의 방법으로 문제를 해결하고 성능을 향상시킬 수 있습니다.
강의를 통해 Backpropagation과 성능 향상에 대한 흐름을 잘 이해할 수 있었습니다! : )
투빅스 15기 김동현
NLP를 역전파와 연관지어 자세히 알아볼 수 있는 시간이였습니다.
- BackPropagation은 output vector 를 Weight matrix 에 대해 미분하고, FeedForward 과정을 통해 나온 predict 값과 실제 값을 통해, error signal vector를 만들고, Chain Rule 을 이용해 가중치를 업데이트 한다.
- pre-trained는 대규모 말뭉치 & 컴퓨팅 파워를 통해 embedding 값을 만들고, 해당 embedding 에는 말뭉치의 의미적, 문법적 맥락이 모두 포함되어 있다.
- fine-tuning는 이후 embedding을 입력으로 하는 새로운 딥러닝 모델을 만든다. 우리가 풀고 싶은 구체적인 task와, 가지고 있는 소규모 데이터에 맞추어, embedding을 포함한 모델 전체를 update 한다.
- Vanishing Gradient는 sigmoid 함수의 미분값의 범위가 (0, 1/4] 가 되어, 작은 값이 계속적으로 곱해지는 것이기 때문에 gradient 값이 0으로 사라지게 되므로, Activation Function, Weight Initialization 으로 해결한다.
- Dying ReLU는 input으로 음수가 들어오게 되면, Backpropagation 진행 시 0 값이 곱해지게 되어 사라져 버리는 문제가 발생하게 되므로, BatchNormalization, Optimization 으로 해결한다.
- Overfitting은 가지고 있는 데이터에 지나치게 맞추어 학습하여, 새로운 데이터셋에 대해 제대로 예측하지 못하게 되므로, Regularization, Dropout 으로 해결한다.
투빅스 15기 이윤정
- NLP는 task를 수행하는 과정에서 벡터를 결합한 matrix 전제를 input으로 넘겨주지 않고 window 단위로 넘겨주어 단어 벡터가 task에 도움이 되는 방향으로 가중치를 업데이트 한다. 하지만, 이러한 방식이 항상 좋은 결과를 만들진 못한다. 만약 학습시키는 데이터 셋에 특정 단어가 없다면 해당 단어는 다른 단어와 유사한 의미를 지니고 있어도 다른 의미를 지닌 단어로 분류되기 때문이다.
- 이러한 문제를 해결하기 위해 Pre-trained 모델을 사용한다. 이미 방대한 양의 데이터에 대해 학습을 마친 상태이므로 train 데이터 셋에 포함 유무와 관련 없이 유사 관계가 형성되기 때문이다. Fine Tunig의 경우 데이터 셋의 규모에 따라 유무가 달라진다.
- Numerical Gradient(수치적 방법)은 미분값을 쉽게 얻을 수 있지만 그만큼 연산량이 증가한다는 단점이 존재한다. 이와 달리 Chain Rule을 통한 Analytic Gradient(해석적 방법)은 계산 방법은 정확하고 빠르지만 실수가 발생할 수 있다는 단점이 존재한다. 이러한 단점은 Numerical Gradient Check 방식을 통해 보완할 수 있다.
- 과적합은 손실함수에 규제항을 추가하는 Regularization을 통해 방지할 수 있다. 주로 R2 규제항을 사용한다.
투빅스 15기 조효원
Gradient를 계산하는 방법에는 Numerical Gradient와 Analytic Gradient가 존재하는데, 각각은 미분 공식을 이용하고 Chain rule을 이용한다. 이때, Analytic Gradient 방식을 사용하면 빠르고 대체적으로 정확하지만 실수가 발생할 수 있다는 단점이 있고, Numerical Gradient 방식은 연산량이 너무 커서 실질적으로 사용하기 어렵다는 단점이 있다.
NLP에서는 벡터 전체 단위로 학습을 하지 않고 window 단위로 학습을 진행한다. 수행할 작업에 맞춰서 가중치와 단어 벡터들이 업데이트되는데, 이때 특정 단어가 코퍼스 내에 등장하지 않거나 매우 적게 등장하는 경우 문제가 된다. 따라서 retraining은 권하지 않으며, 큰 단위로 학습된 pretrained 모델을 사용하는 것을 권장한다. 가지고 있는 데이터의 크기가 100만 개 이상일 때는 fine-tuning을 진행하는 것이 성능 향상에 도움이 되지만, 이보다 적다면 성능에 문제를 야기한다.
이 밖에도 신경망을 보다 빠르고 정확하게 학습시키기 위한 방법으로 overfitting을 막는 regularization 방식, 학습시간 감소를 위한 Vectorization, 비선형성, parameter Initialization, Optimizer, Learning Rate 등에 대한 구체적인 예시들을 확인했다.
투빅스 14기 강의정
Lecture 4. Backpropagation and Computation Graphs를 주제로 발표해주셨습니다.
- Word에 대한 미분을할 때 window 단위로 가중치를 업데이트를 하는 방식은 특정단어가 학습 데이터 셋에 포함되지 않는다는 이유로 업데이트되지 않는 문제가 있습니다. 이를 위해 Pre-trained 모델을 사용할 수 있고, Training Dataset이 100만개 이상으로 많을 경우 Fine Tuning을 하면 좋습니다.
- back propagation에서 효율적인 처리를 위해 Chain Rule을 설계하여 값을 대입하면 바로 미분값을 얻도록 할 수 있습니다. 그렇게되면 순전파와 역전파의 시간복잡도는 동일하게 됩니다.
- Gradient를 계산하는 방법에는 Analytic Gradient와 Numerical Gradient가 있습니다.
- Analytic Gradient는 Chain Rule을 이용하여 계산하는 방식입니다.
- Numerical Gradient는 해당 파라미터의 미분을 구하기 위해 미분의 공식을 이용해 계산을 하는 방법입니다.
- Neural Networks의 성능을 높이기 위한 방법으로 Regularization, Vectorization, Non-Linearities, Parameter Initialization, Optimizers, Learning Rates들을 다루었습니다.
투빅스 15기 김재희
역전파 과정과 편리한 역전파 계산을 위한 그래프에 대해 다뤘습니다.
-
본래 각 파라미터가 손실함수에 대해 어떤 방향을 가지는지 보려면 손실함수에 대해 직접 각 파라미터를 미분해야 합니다. 하지만 손실함수는 복잡하고, 이를 각 파라미터에 대해 미분하는 과정 역시 복잡할 수 밖에 없습니다. 이를 편미분과 chian rule을 이용해 간단하게 만들 수 있습니다.
-
chain rule을 이용할 경우 이전 층의 그래디언트가 이번 층의 미분에 직접 사용되게 됩니다. 이를 이용하여 중복된 계산을 줄일 수 있습니다.
-
gradient descent 만으론 효과적인 학습이 힘듭니다. 이를 개선하기 위해 다음과 같은 방법들이 사용될 수 있습니다.
- regulariation: 파라미터 크기를 제약하여 모델을 간단하게 만들어 줍니다.
- vectorization: 파이썬 연산시 벡터화를 이용하면 list comprehension보다 빠른 연산이 가능합니다 .
- 다양한 비선형 함수: sigmoid는 vanishing gradient 문제가 쉽게 발생합니다. 이를 개선하고자 tanh, hard tanh, ReLU 등이 등장했습니다. 특히 ReLU 특유의 간단함과 좋은 성능으로 현재도 다양한 파생형이 나오고 있습니다 .
- initialization: 파라미터 초기화 시 특정 범위 내로 값을 제한하여 더욱 효과적인 학습이 가능합니다.
- Optimizer: 옵티마이저는 종류가 다양합니다. 보통 Adam이 표준적으로 사용되고 있습니다.
투빅스 14기 정재윤
- Backpropagation은 ML 부분에서 중요한 부분이다. 기본적으로 Chain rule을 바탕으로 진행되며 특히 차원을 고려하면서 진행해야한다. 또한 Downstream gradient = upstream gradient * local gradient임을 알고 연산해야한다.
- NN을 구성하기 위해 여러가지를 고려해야하는데, 강의에서는 약 6가지를 언급했다. 우선 과적합을 방지하기 위한 Regularization, 연산의 효율을 위한 vectorization, Non-linearities, Parameter Initialization, Optimizers, Learning Rates 등을 고려해야한다.
투빅스 14기 박준영
이번강의는 투빅스 15기 조준혁님이 진행해주셨습니다.
- Neural Network에서 chain rule을 이용하여 가중치를 업데이트 합니다.
- NLP에서는 단어를 window 단위로 나누고 vector을 만들어 가중치 업데이트를 진행한다.
- 하지만 데이터 셋에 단어가 없을 경우 가중치가 업데이트가 불가능해서 실제로는 같은 비슷한 의미를 가졌지만 다른 의미를 가진 의미로 분류될 수 있다. 이럴경우 pre-trained 된 모델을 사용하면 된다. 하지만 100만개 이상이면 모델을 학습시켜도 된다.
- Neural Network의 overfitting을 방지하기 위해 Regularization 방법을 사용한다.
역전파 개념을 다시 복습할 수 있어서 좋았고. Neural Network의 다양한 기법들을 배울 수 있었던 유익한 강의였습니다. 감사합니다!










투빅스 14기 한유진
역전파에 대한 개념을 다시 한번 잡을 수 있어서 좋았고, 왜 이러한 것들이 등장하게 되었는지와 같은 흐름도 잘 짚어주셔서 내용을 이해하는데 많은 도움이 되었습니다! 좋은 강의 너무 감사합니다!