작성자: 건국대학교 응용통계학과 주지훈

contents

1. Classification review/introduction
2. Neural Networks introduction
3. Neural Networks in NLP
4. Matrix calculus

1. Classification review/introduction

Classification

위와 같은 training dataset이 있을 때
$x_{i}$(input): 단어나 문장, 문서 등
$y_{i}$(output): 우리가 예측하고자 하는 label이나 class(sentiment, named entities, buy/sell decision)

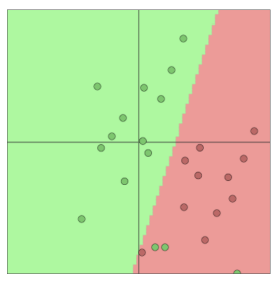
우리의 목표는 초록색과 빨간색을 분류하는 선을 찾는 것입니다.

• ML/Deep Learning 방법으로 분류
• 분류: 비슷한 output끼리 모이도록 경계를 긋는 것
• 전통적인 ML/Stats 접근: softmax/logistic regression을 이용해서 output의 class를 구분할 경계선을 결정하는 것을 의미

softmax classifier

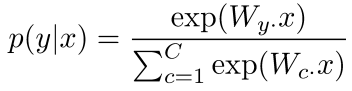
softmax는 input $x_{i}$를 확률 $p_{i}$로 바꿔주며, 분류하고 싶은 class의 수만큼 확률값을 구성합니다. 이때 모든 class의 확률값을 다 더하면 1이 됩니다.

Step 1

• weight matrix인 W에는 각 클래스의 y번째 행과 x의 행을 곱하면 class와 관련된 score가 나옵니다.

• 즉 선형결합으로 구성된 $f_{y}$가 나오게 됩니다.

Step 2

• step1에서 나온 score를 softmax function에 넣으면 softmax는 이를 확률분포로 바꿔줍니다.
• 즉 0과 1 사이의 수로 정규화가 됩니다.

Cross-entropy loss

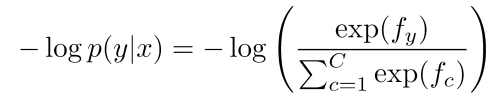
우리의 목표는 각각의 training example (x,y)에 대해 y의 확률을 최대화하는 것입니다.

• 확률을 최대화 = 로그확률을 최대화 = 음의 로그 확률을 최소화

따라서 우리는 이제 위의 식을 최소화할 것입니다.

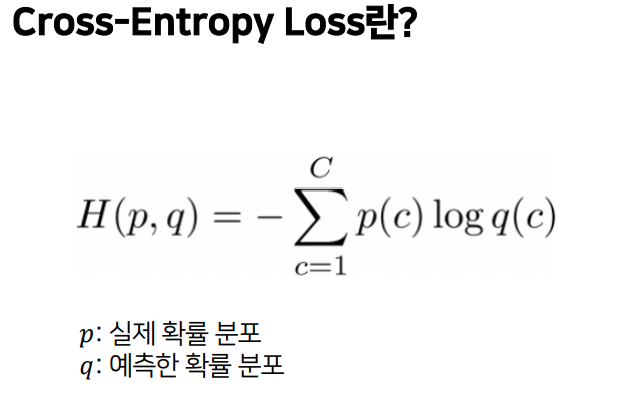
• 옳은 클래스에만 1을, 나머지는 0을 부여
• $p=[0,...,0,1,0,...,0]$
• 잘못 분류한 확률들은 0으로 사라지고 실제 class의 음의 로그 확률값만 남습니다.

앞서 봤던 cross-entropy loss식을 $i=1$부터 N까지의 평균을 구해주면 full dataset의 loss함수가 됩니다.

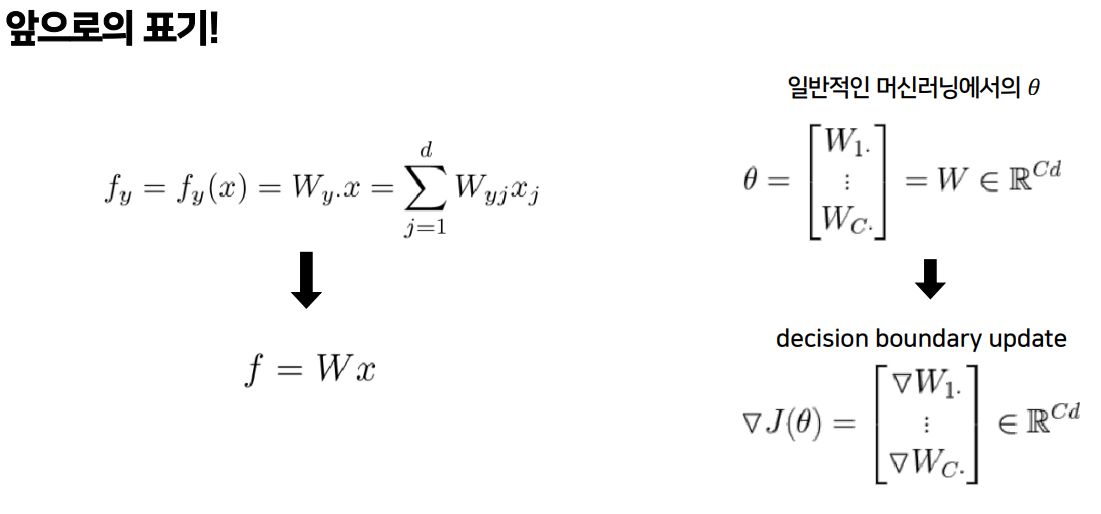
• 기존 ML 최적화의 매개변수는 서로 다른 클래스에 대한 가중치의 집합
• 우리는 $c*d$를 한 W행렬을 가지고 있으며 이것이 우리 모델의 매개변수

Softmax의 문제점

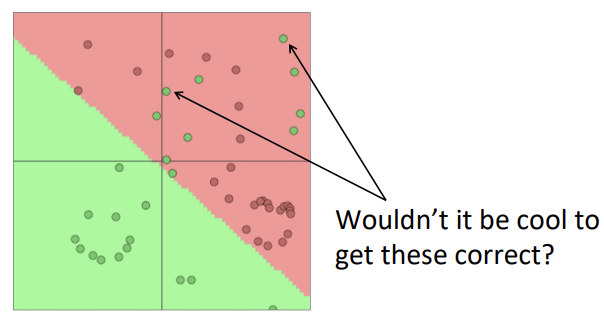
위의 그림에서 빨간색으로 분류된 영역에 초록색 점들이 섞여있는 것을 보실 수 있습니다. softmax는 선형분류만 가능하기 때문에 선 하나로 분류가 안 되는 복잡한 문제를 풀 수 없습니다.

그런데 이 문제는 Neural Network를 통해 해결할 수 있습니다.

2. Neural Networks Introduction

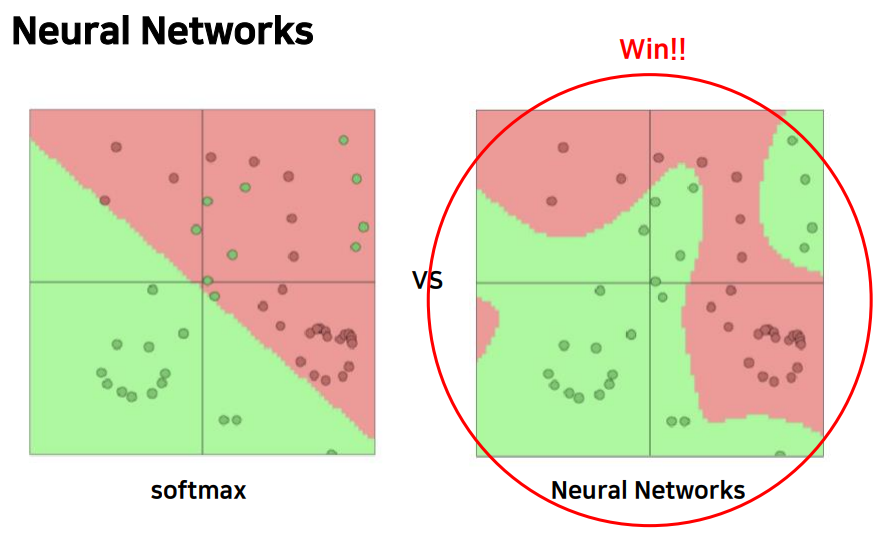
위의 그림과 같이 neural network를 사용함으로써 nonlinear seperable 문제도 풀 수 있게 됐습니다.

전통적인 classification과의 차이

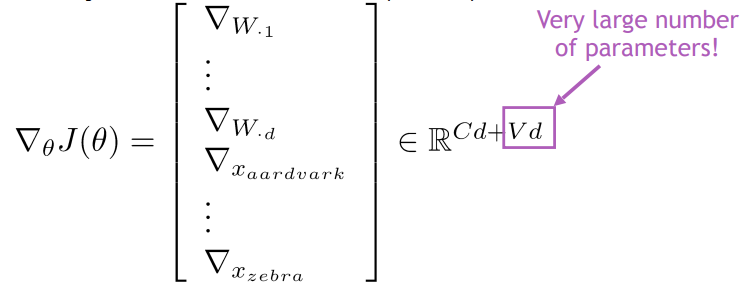1. W와 Word vector 모두 학습

• 단순 선형 분류기로 분류하면 bias가 나타나는 문제 발생
• 전통적인 방법에서는 W만 학습했지만 NLP에서는 word vector $x$도 같이 학습합니다.
  
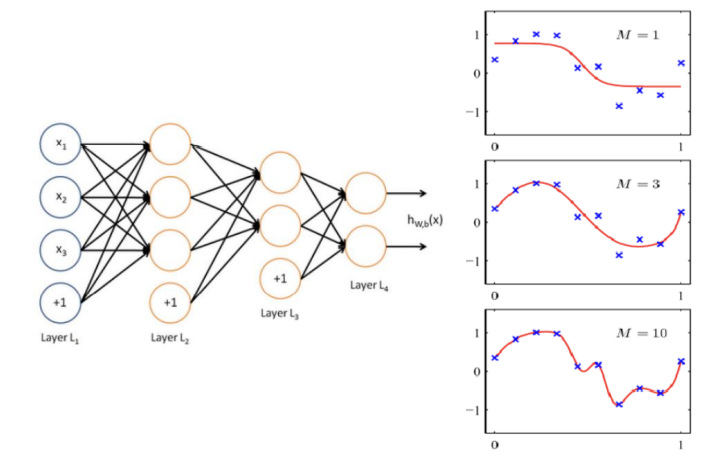
  2. Deeper MLP
• Layer들을 기게 쌓으면서 더 복잡한 문제를 푸는 것이 가능해졌습니다.
• 오른쪽 그림을 보면, layer가 깊어질수록 선이 정교해지는 것을 알 수 있습니다.

Neural Network 복습

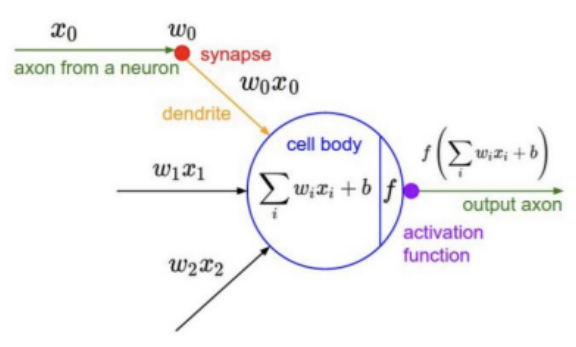
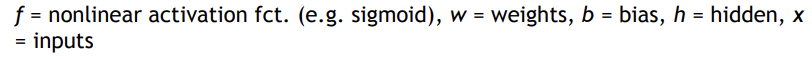
• 입력: $x_{0}, x_{1}, x_{2}$
• 가중치 $W_{0}, W_{1}, W_{2}$를 곱하여 모델링
• cell body에서 합산, 여기서 자체적인 bias 가집니다.
• $h_{w,b}(x) = f(w^Tx+b)$
• 활성화함수 f를 거쳐 output이 나옵니다.
• 활성화함수: $f(z)=\frac{1}{1+e^{-z}}$
• 파라미터: $W, b$
  
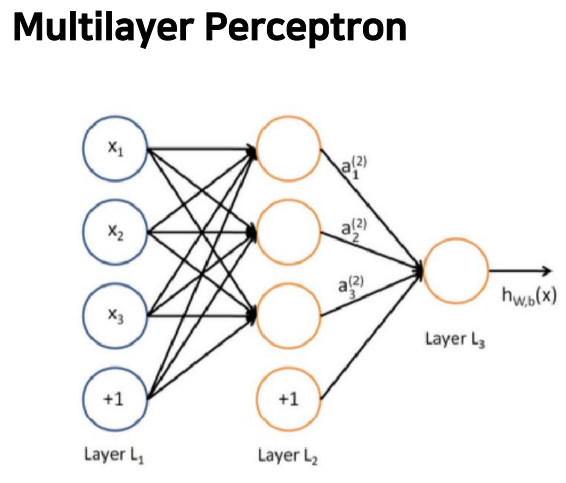
  오류역전파란 은닉층을 추가시켜 쉬운 방법으로 weight를 계산하는 것을 말합니다. 이때 input에 bias 역할을 하는 +1이 추가되고, hidden layer에도 마찬가지로 +1이 추가됩니다. 원래 d개의 입력노드, h개의 hidden layer 노드가 있었다고 하면 d+1개의 입력노드, h+1개의 hidden layer 노드를 가지게 됩니다. 그리고 출력을 c개라고 하면, 파라미터의 수(W의 수)는 $(d+1)*h+(h+1)*c$가 됩니다.

이때 각각의 파라미터의 값들을 모두 업데이트 해주는 것이 핵심이고, 앞으로 우리는 이 과정을 할 것입니다!

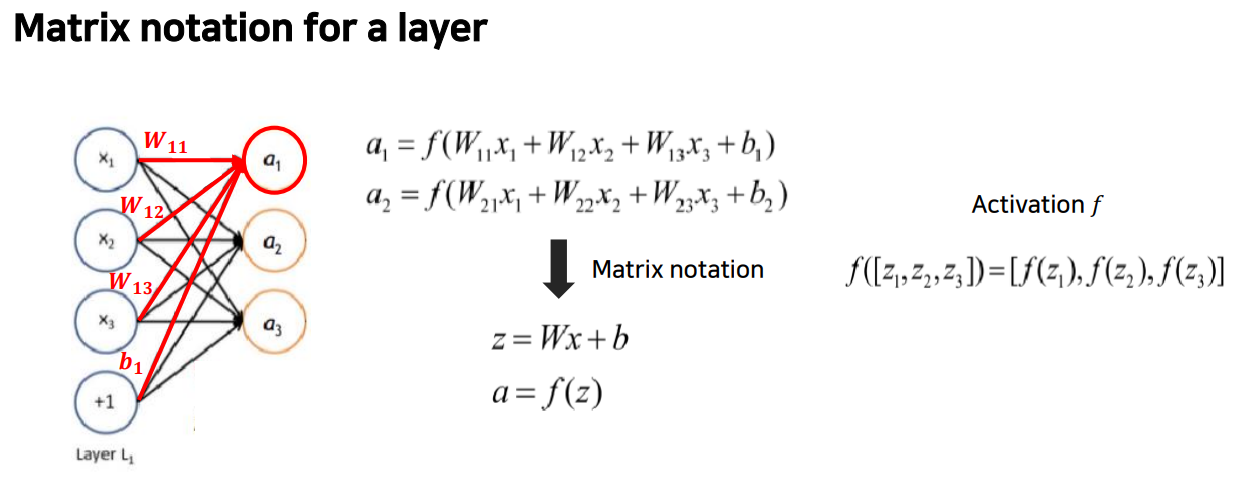
위의 그림은 신경망의 레이어입니다. 왼쪽은 입력벡터, 오른쪽은 출력 벡터이고, 모든 것이 연결되어 있으며 검은색 선을 따라 가중치를 갖게 됩니다. 완전히 연결된 레이어는 행렬이고, 레이어의 효과를 계산하기 위해 행렬 표기법으로 축소하였습니다. 이렇게 계산한 $z$는 활성화 함수 $f(z)$에 넣습니다. $f(z)$는 요소별로 적용하고, 결과도 벡터로 나옵니다.

3. Neural Network in NLP

Named Entity Recognition(NER)

• 개체명 인식(NER): 인명, 지명 등 고유명사를 분류하는 방법론
  많은 텍스트에서 자동으로 지식 기반 구축을 시작하려는 경우 일반적으로 하고 싶은 것은 명명된 entity를 가져와서 이들간의 관계를 파악하는 것입니다.

Possible Purpose

• 문서에서 특정entity에 대한 언급 추적
• 질무에 대한 답변의 경우, 답변은 보통 인명
• 요구되는 많은 정보들은 인명간의 관계에 관한 것인 경우가 많습니다.
• 동일한 기술들이 다른 slot-filling classification으로 확장될 수 있습니다.

BIO 방법

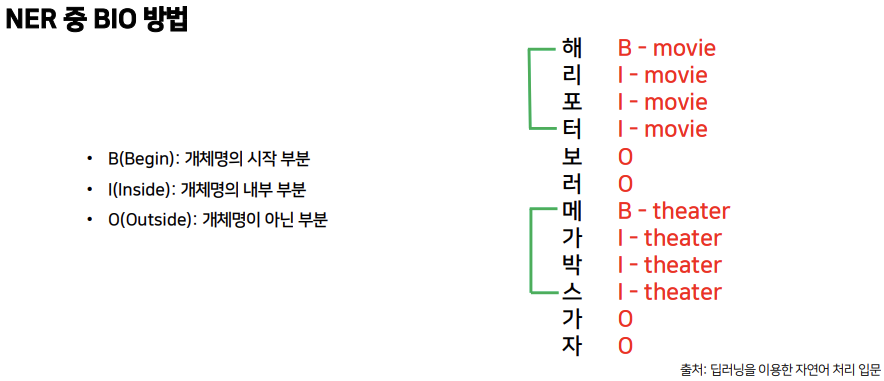
개체명의 시작 부분은 B, 개체명의 내부 부분은 I, 개체명이 아닌 부분에는 O를 써주고, 이와 함께 어떤 종류의 개체인지도 써줍니다.

NER의 한계

• 문제

1. entity의 경계를 정하기가 어렵습니다. ex) 'First National Bank' or 'National Bank'
2. 무엇이 entity인지 알기 어렵습니다. ex) 이름이 'Future School'인 학교 or 미래의 학교
3. 모르는 entity에 대해 class를 아는 것이 힘듭니다. ex) 'Zig Ziglar'(사람)의 class를 알기 위해 Zig Ziglar에 대해 더 찾아봐야 한다.
4. Entity class는 애매모호하고 문맥에 의존합니다.
   ex) 아래 문장에서 'Charles Schwab'는 보통 조직으로 사용되지만 여기서는 사람으로 사용

Binary word window classification

single word로만 word classification을 하는 경우는 굉장히 드물고, 보통 문맥 안에서 이루어집니다.

• ex) auto-antonyms(자동-반의어)
  "To sanction" can mean "to permit" or "to punish”
  "To seed" can mean "to place seeds" or "to remove seeds"
  "제재하다(sanction)"는 무언가를 허락하는 경계선을 주는 것인지 아니면 벌을 주는 것인지 문맥을 고려하여 둘 중 하나를 선택해야 합니다.

이 문제를 해결한 것이 바로 문맥까지 고려하는 Window Classification입니다.

Window Classification

• Idea: 중심 단어와 주변 단어들(context)를 함께 분류 문제에 활용
• 가장 간단한 방법은 window에 있는 word vector들을 평균내고 그 평균 벡터로 분류하는 것.
• 문제: 위치 정보를 잃어버려서 실제로 그 단어 벡터 중 어떤 것이 분류하려는 것인지 알 수 없음.
• 해결: Multi Perceptron, Softmax

Window classification: Softmax

window 내에서 word vector와 주변 벡터들을 합친 후 softmax classifier를 훈련시켜 분류하는 방법입니다.

• Paris가 이름인지 지명인지 분류하기: Paris와 Paris의 왼쪽 2개, 오른쪽 2개 즉 총 5개의 word vector들을 합쳐서 5d 크기의 vector 형성하고, 이를 이용해 classifier 제작.

$x$대신 $x_{window}$를 input으로 하여 softmax 적용시킵니다.
또한 word2vec에서는 corpus내 모든 위치에 대해서 학습했지만, 이번에는 높은 score를 가지는 위치에 대해서만 집중적으로 학습합니다. 아래의 예시를 통해 자세히 살펴보겠습니다.위 예제 문장에서 $X_{Paris}$가 'Location'으로 분류되는가?

True window

오로지 위의 window만이 Paris가 중앙에 있으므로 'True window'

Corrupt window

Paris가 중앙에 있지 않은 window들은 모두 'Corrupt window'

이때 중앙에 Location name이 있으면 높은 score를, 없으면 낮은 score를 return합니다.

3-layer neural net

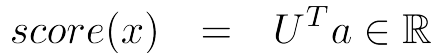
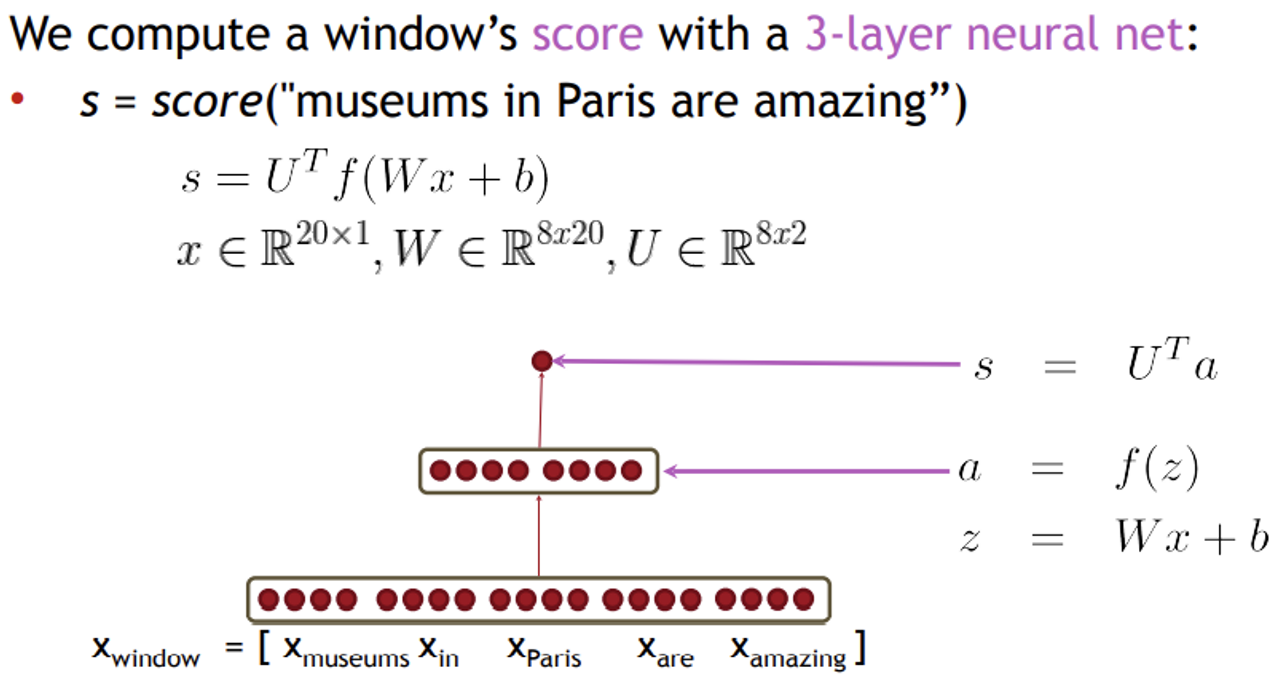
input인 $20*1$벡터를 가진 $x$에 $8*20$을 가진 가중치 W를 곱하고 bias를 더하여 활성화함수인 softmax를 거치면 $8*1$ 벡터가 나옵니다. 이제 이 벡터에 $U$를 곱하면 Transpose가 되므로 $1*8$과 $8*1$을 내적하면 $1*1$ 스칼라 값이 나오게 되고 score를 얻을 수 있습니다.

Max-margin loss

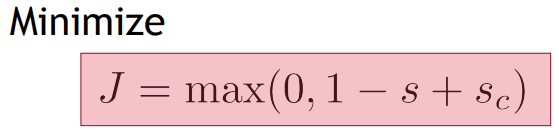
• softmax를 사용하면 값을 확률 비율로 변경하기 때문에 비율간 차이를 계산하는 cross-entropy를 손실함수로 사용
• 하지만 위에서 score 함수를 직접 정의했으므로 여기에서는 이에 걸맞는 max-margin loss 사용
• True window의 score는 더 크게, Corrupt window의 score는 더 작게 만들기 -> input $x$에 대하여 정답과 오답간의 차이를 최대화시키는 손실 함수 $J$

Stochastic Gradient Descent

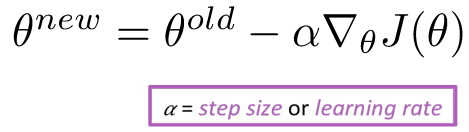
앞으로 max-margin 손실함수를 통해 구한 손실값에 따라 각 파라미터 $W, U, b, X$가 손실값에 얼마나 많은 기여를 했는지 알아보고 해당 기여도에 따라 각 parameter 값 조정할 것입니다.

4. Matrix calculus

Jacobian Matrix

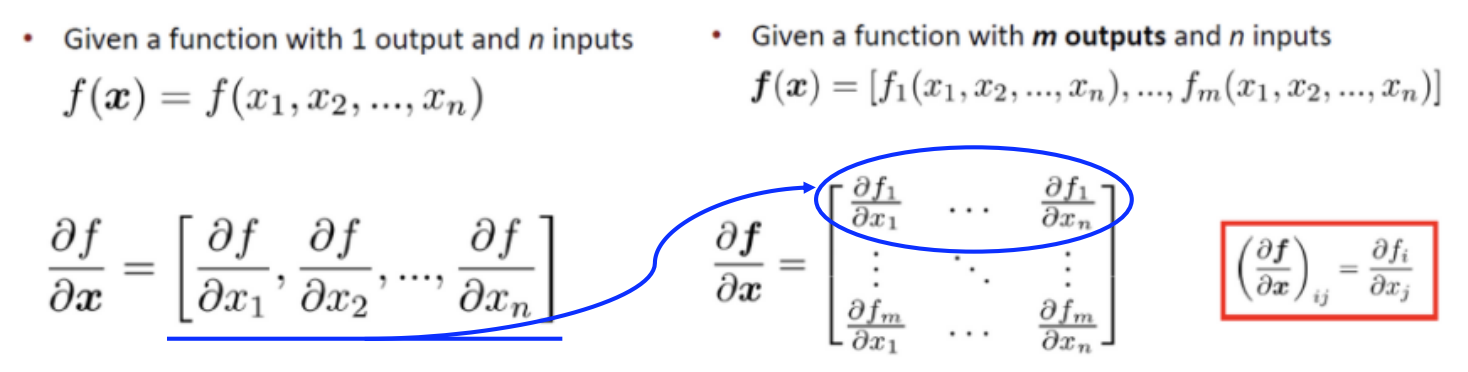
• 왼쪽(함수 한 개의 미분): n개의 input을 넣으면 한 개의 output 산출합니다. 이를 미분하면 n개의 각각의 input으로 미분하여 하나의 벡터가 됩니다.
• 오른쪽(matrix에서의 미분): m개의 함수 각각에 n개의 input이 들어간다고 할 때, 이를 미분하면 input과 output의 모든 조합을 고려하여 $m*n$ matrix가 되고 이를 Jacobian Matrix라고 합니다.

Chain Rule

Multiply Jacobians: $h$를 $x$로 미분하기 위해서는 $h$식을 $z$로 미분한 값에 $z$식을 $x$로 미분한 값을 곱하면 됩니다.

Example Jacobian: Elementwise activation Function

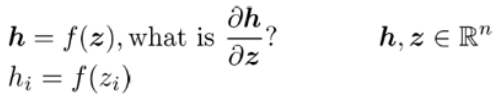
• $h$는 $z(Wx+b)$를 input으로 집어넣어 활성함수를 적용해 나온 식
• n개의 output과 n개의 input을 가진 함수이므로, $h$를 $z$로 미분하면 n*n의 matrix가 나옵니다.
  
• n*n의 matrix를 계속 미분하면 $h_{i}$는 $f(z_{i})$로 나타낼 수 있습니다.
• i=j일 때만 미분 가능하므로 미분하면 대각행렬이 나오게 됩니다.
  
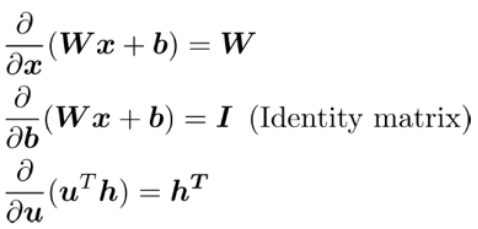
• 첫 번째 식: $Wx+b$를 $x$로 미분하면 $W$(가중치)가 나옵니다.
• 두 번째 식: $Wx+b$를 $b$로 미분하면 $I$(항등행렬)이 나옵니다.
• 세 번째 식: $Wx+b$를 $u$로 미분하면 $h^T$(h의 전치행렬)이 나옵니다.

Back to our Neural Net

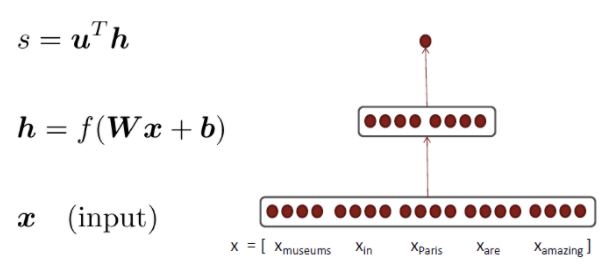
• window of words를 가지고 있고 word vector를 hidden layer에 넣은 다음 벡터 내적을 하여 최종 score를 얻음
• 모델이 모든 parameter($x,W,b,u$)에 따라 어떻게 변하는지
• 원래는 우리가 손실함수로 사용한 max-margin loss를 계산해야 하지만, 강의에서는 쉽게 score의 gradient를 계산해보았습니다.
• Jacobian Matrix+Chain rule+$diag(f'(z))+앞서 나온 세 가지 식 이용

1. $b$에 대한 미분 ${\frac{{\delta}s}{{\delta}b}}$

Step 1: Break up equations into simple pieces

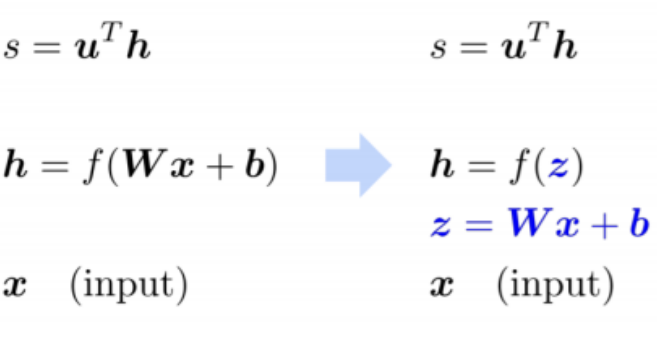
• $Wx+b$를 $z$로 치환

Step 2: Apply the chain rule

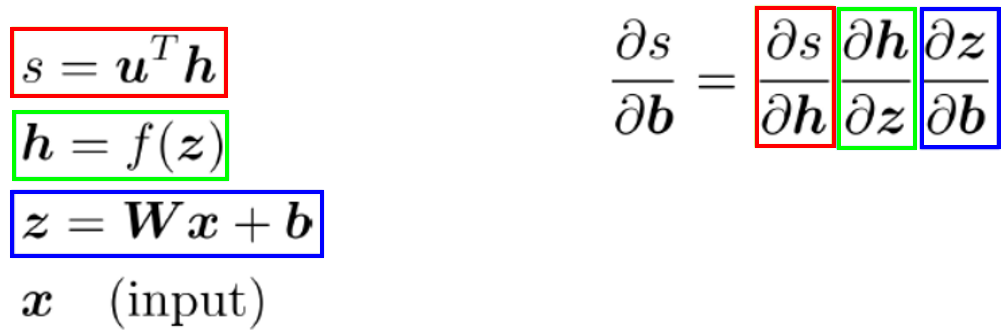
• Chain rule을 통해 $s$를 $b$로 미분하면 각 단계의 도함수의 곱으로 나타낼 수 있습니다.
  
• 이제 지금까지 얻은 식들을 이용해 대입하면 됩니다.
  

2. $W$에 대한 미분 ${\frac{{\delta}s}{{\delta}W}}$

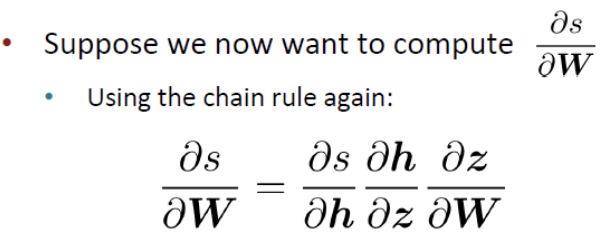
• 같은 방식으로 chain rule을 적용하여 미분합니다.
  
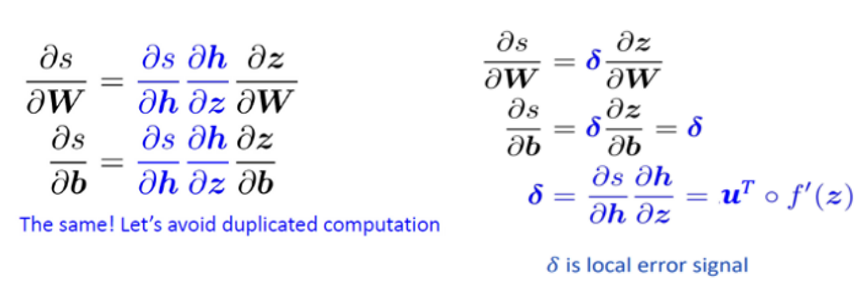
• 앞서 bias로 미분했던 식과 비교해보면, 제일 오른쪽 끝 식만 다를뿐 중간식은 같기 때문에 앞서 계산했던 결과를 그대로 사용할 수 있어 계산량을 줄일 수 있습니다. (오차 역전파의 장점)
• 이때 반복되는 부분을 델타라고 합니다.
  
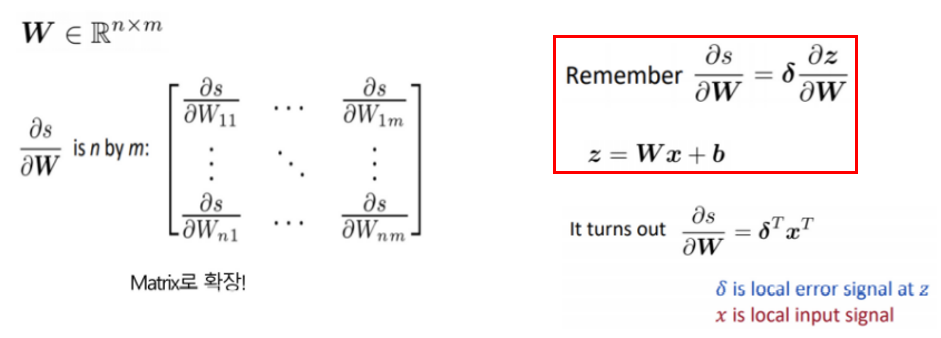
• $W$는 $n*m$ matrix입니다. 앞서 계산한 결과인 빨간색 박스를 이용하면 ${\frac{{\delta}s}{{\delta}W}}={\delta^T}x^T$라는 결과가 도출됩니다.

Transpose를 하는 이유는?

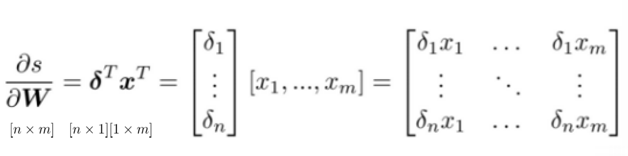
• $n*m$형태의 matrix를 만들기 위해서

---

Reference

• CS224 Winter 2019: Natural Language Processing with Deep Learning
• https://velog.io/@tobigs-text1415/Lecture-3-Word-Window-Classification-Neural-Networks-and-Matrix-Calculus
• https://velog.io/@tobigs-text1314/CS224n-Lecture-3-Word-Window-Classification-Neural-Networks-and-Matrix-Calculus
• https://wikidocs.net/24682
• https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=koys007&logNo=221403872271