발표자 17기 이혁종

원문링크

1. Backgoround

1.1 VAE

VAE 설명

자세한 내용은 위 링크를 참고하시면 됩니다.

간단하게 복습해봅시다.

Encoder와 Decoder의 구조로 되어있습니다.

이때 latent vector의 distribution을 원하는 prior $p(z)$로 근사시키 위해 Loss function에 KL-term이 추가되어 있습니다.

따라서 latent를 원하는 distribution으로 만들 수 있습니다.

1.2 Reparameterizaion trick

$z$를 sampling하여 Decoder를 거쳐 나온 generated image와 원래 image간의 MSE를 계산합니다. 이때 Random node 때문에 backpropagation가 안되므로 위의 사진과 같은 trick을 사용하여 backpropagation을 진행 할 수 있게 합니다.

1.3 GAN

Generative model은 원하는 image를 생성하는 model이지만 원하는 distribution을 생성한다고 해석 할 수 있습니다. 즉, 있을법한 image를 생성하는 것입니다.

위의 그림을 보면 Generator는 Discriminator를 속이도록 즉, 실제 image의 distribution을 만들도록 학습되고 Discriminator는 정확한 구분을 하도록 적대적으로 학습됩니다.

1.4 Information theory

$X$의 정보량을 수식으로 정의하고 싶습니다. 이때 두가지 가정을 해봅시다.
$X$의 정보량을 $h(X)$라고 한다면 이는 $p(X)$와 관련이 있으며 $h(X,Y) = h(X) + h(Y)$일 것입니다.
즉, $P(X)$가 작으면 각각의 $x$가 나타날 확률이 작은 것을 의미하며 이는 정보량 $h(X)$가 높음을 의미합니다.
또한 $X,Y$의 정보량 $h(X,Y)$는 각각의 정보량 $h(X)$와 $h(Y)$를 더한것과 같습니다.
이 두가지를 만족하기 위해서는 정보량 $h(X)$를 다음과 같이 정의하면 됩니다.
$h(X) = - \log_2 p(X)$

또한 이를 이용하여 Entropy를 정의하는데 정보량의 평균으로 정의합니다.
즉, $Entropy(X) \;\; H(X) = - \displaystyle\sum_x p(x) \log_2 p(x)$ 입니다.

이를 이용하여 Conditional Entropy를 정의하면 다음과 같습니다.
$H(y \mid x) = - \displaystyle\int \int p(y,x) \ln p(y \mid x) dy dx = - \int \int p(y,x) \ln \cfrac{p(x,y)}{p(x)} dy dx$

$= - \displaystyle\int \int p(y,x) \ln p(x,y) dy dx + \int \int p(y,x) \ln p(x) dy dx$

$= - \displaystyle\int \int p(y,x) \ln p(x,y) dy dx + \int p(x) \ln p(x) dx$

$= H(x,y) - H(x)$ 입니다.
즉, $x,y$를 표현하기 위한 정보량은 $x$를 표현하고 + $x$가 주어진 상태에서 $y$를 표현하는 정보량 입니다.

또한 Mutual Information도 정의합니다.
$I(x ; y) = KL \Big( p(x,y) \mid \mid p(x)p(y) \Big) = -\displaystyle\int\int p(x,y) \ln \bigg( \cfrac{p(x)p(y)}{p(x,y)} \bigg)dx dy$입니다.
즉, 두개가 얼마나 독립에 가까운지를 나타냅니다.
또한 더 풀면 $I(x ; y) = H(x) - H(x \mid y) = H(y) - H(y \mid x)$입니다.

1.5 Disentanglement, Entanglement and Representation Learning

Convolution based classification model을 생각해 봅시다.
가장 쉬운 모델인 VGG를 생각해봅시다.

Input image가 들어가면 CNN을 지나고 이후 FC를 지나서 target label을 예측합니다.

이때 stacked CNN이 하는 역할은 Feature extractor이고 이후 FC가 하는 역할은 classifier입니다.

즉, 앞단의 CNN이 Image에 대한 정확한 feature를 잘 뽑아 줘야 합니다.
예를들어 Cat / Dog classification인 경우 image에 대한 feature 예를들어 눈, 귀 등을 잘 detect해야 feature map을 classifier에 넘겨 줄때 올바를 classification이 가능합니다.

이렇게 feature map을 잘 뽑게 하는 learning을 representation leraning이라고 하죠.

이를 generative model에서 생각해 본다면 image generation의 source인 latent vector를 잘 알아야 원하는 Image를 generate할 수 있습니다.

Latent vector를 알고 올바르게 학습된다는 것은 latent의 어느 부분인 generate되는 image의 어느 부분에 변화를 주는지 안다는 의미 입니다.

이를 연장해서 생각해 보면 latent vector의 각각의 element는 서로 다른 feature를 capture해야 합니다.
즉, feature가 분리되어 있다면 좋은 겁니다.

예를들어 latent에서 하나만 바꿨는데 눈,코,입의 모양이 모두 바뀐다면 원하는 image를 생성하는데 어려움이 있을겁니다. 우리는 각각이 independent하게 작동하기를 원합니다.

이렇게 latent space에서 feature를 분리하는 것은 Disentanglement라고 합니다.
반대로 서로 엉켜있는것은 Entanglement라고 합니다.

2. Deep Convolutional Inverse Graphics Network

Nips 2015 paper입니다.

원문에 대한 자세한 설명은 아래 링크를 참고해 주세요
Paper review

DC-IGN에서 IGN은 단순히 transposed convolution연산을 의미합니다.
DC-IGN은 VAE와 거의 같습니다.

2.1 Architecture

Model의 architecture는 다음과 같습니다.

Encoder부분은 Conv연산이고 Decoder부분은 TransposedConv연산입니다.

이는 VAE에서 Disentanglement를 가능하게 한 연구입니다.

구조와 Object Function모두 유사하지만 중간에 mini-batch에 변화를 주어 이를 가능하게 했습니다.

Latent vector는 Image를 generate하는데 source역할을 합니다.
그렇다면 latent를 잘 조정한다면 원하는 image를 얻을수 있어야 합니다. 이것이 가능한것이 좋은 model입니다.
물론 VAE와 AAE는 latent space의 distribution을 조정했지만 단순히 그것뿐이지 generated image를 직접 조정하지는 못합니다.

본 논문은 이를 가능하게 하는 즉, Disentanglement를 가능하게 하는 방법을 소개합니다.

DC-IGN은 해석 가능한 image의 representation을 학습 할 수 있습니다. 이것이 Disentanglement입니다.

이제 model을 전반적으로 설명하겠습니다.

Encoder의 output을 $encoder(x) = y_e$라고 하겠습니다.
이는 원하는 분포인 $Q(z_i \mid y_e)$를 만드는데 사용됩니다.
우선 KL를 사용하기 위해 $Q \sim MN$으로 가정합니다.
그리고 $y_e$를 이용하여 $MN$의 mean과 variance를 만듭니다.
이를 수식으로 표현하면 다음과 같습니다.

$\mu_{z_i} = W_e * y_e$
$\Sigma_{z_i} = diag(exp(W_e * y_e))$
$\forall i, z_i \sim \mathcal{N}(\mu_{z_i}, \Sigma_{z_i})$

중간에 $W_e$가 들어가는데 이는 그냥 Linear한번 들어가는 것이라고 생각하면 됩니다.

즉, image $x$가 주어지면 Encoder를 거쳐 나온 $y_e$를 이용하여 $MN$의 statistics를 계산합니다.
그리고 계산된 Distribution에서 $z$를 sampling하여 Decoder로 보내면 됩니다.

여기까지 해서 VAE와 차이점을 생각해본다면 VAE는 Encoder의 output이 바로 $MN$이 되는 반면 여기서는 $W_e$를 거쳐 이를 Statistics로 하는 $MN$이 되는 겁니다. 뭐 같습니다.

다음은 Decoder에서 나온 generated image로는 MSE를 latent로는 KL을 계산하면 됩니다.

그럼 VAE랑 뭐가 달라서 Disentanglement가 되는 것일까요?

2.2 Disentanglement

논문을 보면 위의 사진 처럼 $z$를 만들겠다고 합니다.

이때 $z_1$부터 $z_3$은 Disentangled vector이고 $z_4$부터 $z_{200}$은 Entangled입니다. Face image로 학습했습니다.
$\phi$는 azimuth of the face, $\alpha$는 elevation of the face, $\phi_L$은 azimuth of the light source입니다.

즉, face image로 학습하여 latent를 만드는데 촬영자의 높이, 얼굴의 각도, 광원의 각도는 정확히 분리 할 것이고 나머지는 그냥 엉켜있게 학습할 것입니다.

위 세가지 feature에 대한 vector element를 extrinsic variable 나머지는 intrinsic variable이라고 하겠습니다.

이를 하기위해서 mini-batch를 구성할때 기존과의 변화를 주었습니다.

2.3 Mini Batch

총 4가지의 mini-batch를 구성합니다.
세가지는 앞에서 언급한 세가지 feature를 하나씩 고정한 다음 나머지를 모두 동일하게 만듭니다.
예를들어 광원의 각도라면 해당 mini-batch는 나머지의 feature가 모두 동일하면서 광원의 각도만 다른 image들로 구성되는 것입니다.
이렇게 세가지를 만들고 나머지 하나는 세가지의 feature를 고정한 상태에서 나머지 feature를 바꾸어 구성합니다.

그럼 이제 총 4가지의 mini-batch를 얻었습니다.

2.4 Training

다음 과정은 다음과 같습니다.

위의 순서로 진행합니다.
원문을 이해하는게 생각보다 어렵다고 느껴 추가적인 설명을 곁들여 아래에서 다시 서술합니다.

1. 4개 중 어떤 feature를 학습할 지 선택합니다. 예를들어 광원의 각도라고 하겠습니다.
2. 선택된 feature만 변화되는 mini-batch를 선택합니다.
3. 해당 mini-batch를 Encoder에 통과시켜 latent를 얻습니다.
4. 4개의 mini-batch 모두를 다시 Encoder에 통과시zu latent를 얻습니다.
5. 광원의 각도에 해당되는 vector element가 $z_3$입니다.
   3번에서 얻은 latent vector에서 $z_3$를 제외한 모든 element를 4번에서 얻은 latent vector의 평균으로 대체합니다. 이 과정을 clamped 되었다고 합니다.
6. Clamped vector를 Decoder에 통과시켜 reconstruction error 즉, MSE를 계산하고 backpropagation을 이용하여 Decoder의 gradient를 얻습니다.
   Encoder까지 안갑니다.!
7. 5에서는 feed forward를 건들였다면 이번에는 backward를 건듭니다.
   마찬가지로 $z_3$이 아닌 element의 gradient는 평균과의 차이를 계산하여 이 값들로 대신합니다.
8. 변화된 gradeint로 Encoder의 backpropagation을 진행하고 SGVB를 이용한 update를 합니다.

단 이때 intrinsic은 고차원이므로 학습되기 힘들어 1:1:1:10의 비율로 학습을 진행합니다. ( 그만큼의 빈도로 update를 합니다. )

2.5 Why?

이렇게 하는것이 왜 Disentagled가 될까요?

원문에 잘 설명되어 있습니다.

이렇게 학습을 하면 $z_3$에서만 해당 mini-batch의 변화를 학습하게 됩니다. 즉, 광원의 각도를 제외한 latent vector element는 평균으로 대체 되었으니 $z_3$만이 광원의 각도의 변화를 학습 할 수 있는 것입니다.
따라서 latent space에서 $z_3$는 광원의 각도의 변화를 잘 학습할 수 있는 것입니다.

2.6 Results

결과는 다음과 같습니다.

(a)는 elevation of the face에 해당하는 $z$만 변화를 주고 나머지는 고정시킨 결과이고 (b)는 azimuth of the face입니다.

3. Info GAN

Nips 2016 paper입니다.

Info GAN은 GAN에 information-theoritic extension을 추가하여 Object function의 작은 변화만으로 해석가능하고 의미있는 representation을 학습 시킬수 있습니다.

3.1 latent code $c$

GAN은 random noise $z$로만 image generation을 수행했습니다.
Info-GAN에서는 이를 두가지로 나눕니다.
먼저 용어부터 정리하고 넘어가자면 latent가 엉켜있는것을 entangled 풀어져 있는것은 disentangled라고 하며 본 논문에서는 순서대로 unstructure, structure라고도 표현합니다.

즉, GAN은 unstructured noise vector만 존재하는 것입니다.

Info-GAN은 한가지를 더 추가합니다.

$z$ : 더이상 압축이 되지 않는 noise의 source입니다.
$c$ : Data distribution에서 중요한 structured semantic feature를 target으로 하는 latent code입니다.

이때 $c_i$들은 독립을 가정합니다.

따라서 generator는 incompressible noise $z$와 latent code $c$를 사용하여 $G(z, c)$를 만들어 냅니다.

여기서 문제가 있는데 추가적인 제한을 두지 않고 원래의 GAN을 사용한다면 $P_G(x \mid c) = P_G(x)$로 학습될 수 있습니다. 즉, $c$의 역할이 없어지는 것입니다.

3.2 Information-theoretic regularization

따라서 information-theoretic regularization을 사용합니다.
즉, $I(c ; G(z, c))$를 높혀줘야 합니다.

이는 두개가 독립이면 0이고 연관이 많으면 높은 값을 가집니다. 즉, 이를 높인다는 것은 둘이 독립이 안되게 하는 것입니다.

이는 다음과 같이 해석될 수 있습니다.
= $x \sim P_G(x)$가 주어졌을 때, $P_G(x \mid x)$의 entropy가 작아야 한다.
= $G(z,x)$가 만들어 질때 $c$의 정보의 손실이 일어나면 안된다.

하지만 $I(c ; G(z,c))$를 maximize하는 것은 어려우므로 근사적으로 maximize합니다.

3.3 Variational mutual information maximization

$I(c ; G(z,c))$의 lower bound는 쉽게 구할 수 있습니다. 따라서 lower bound를 maximize한다면 $I(c ; G(z,c))$역시 어느정도 이상으로 커진다는 것을 기대할 수 있습니다.

근사식은 다음과 같습니다.

즉,

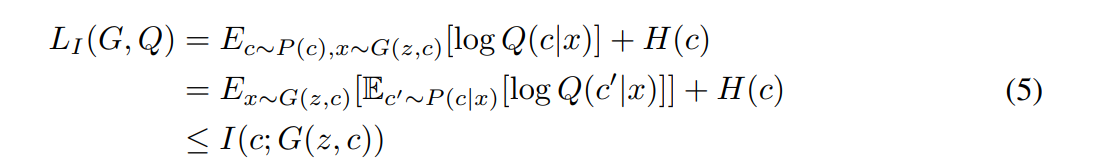
이때 (5)의 두번째의 왼쪽 항은 reconstruction입니다.
즉, c 가 Generator를 지나고 Q를 지나서 나온 $c'$와의 MSE가 됩니다.
아래 그림을 보면서 다시 설명.

따라서 Info-GAN의 Object function은 다음과 같이 정의됩니다.
$\displaystyle\min_{G,Q} \max_{D} \; V_{InfoGAN} (D,G,Q) = V(D,G) - \lambda L_I (G,Q)$
$V(D,G)$는 GAN loss로 $E_{x \sim p_{data}(x)}\bigg(\log D(x)\bigg) + E_{z \sim p_z(z)}\bigg(\log \Big(1-D\big(G(z)\big)\Big)\bigg)$ 입니다.

3.4 Architecture and training.

구조를 보면 다음과 같습니다.

출처

Discriminator는 share하고 이후 FC하나를 추가하여 Q의 distribution을 만들어 $c'$을 만들어 줍니다. 앞에서 이는 reconstruction이라고 했으니 단순히 MSE로 계산하면 됩니다.

예를들어 Mnist이면 $c$는 12-dim이고 10개는 숫자이고 두개는 uniform에서 sampling하여 크기와 각도를 나타내게 합니다. 따라서 10개에 대해서는 CEE 두개에 대해서는 MSE를 사용합니다.

3.5 Results

latent code는 바꾸고 noise는 고정한 결과입니다.
앞에서 12-dim이라고 했는데 (a)는 숫자에 대한 10개의 결과 (c),(d)는 회전과 굵기입니다.

latent code를 countinuous하게 바꾼 결과가 잘 나온것을 확인할 수 있습니다.

3D chair의 결과입니다.
아래서 설명하겠지만 (b)를 자세하게 보면 제대로된 disentanlgement가 안된것을 확인할 수 있습니다.

SVHN의 결과입니다.
(b)에서 숫자도 바뀌는 것을 확인할 수 있습니다.

CelebA의 결과입니다.

4. $\beta$ VAE

ICLR 2017 paper입니다.

Info-GAN은 좋은 model이지만 한계점이 있습니다.
우선 GAN based model이므로 optimization이 어렵습니다. 또한 data에 대한 사전 지식이 필요합니다.
추가로 disentanglement가 얼마나 잘 되었는지에 대한 metric역시 존재 하지 않습니다.
본 연구에서는 VAE based의 $\beta$ VAE를 제안합니다.
추가로 degree of disentanglement를 측정하는 방법역시 제안합니다.

4.1 Preview

이름 그대로 VAE에서 $\beta$만 추가했습니다.
심지어 이거 contant입니다.

VAE의 Loss는

입니다.

$\beta$ VAE의 Loss는

$E _{q_\phi(Z \mid X)}\Big( \log P_\theta(X \mid Z) \Big) + \beta D_{KL}\Big( q_{\phi}(Z \mid X) \mid \mid p(Z) \Big)$ 입니다.

$\beta = 1$ 이면 완전히 같아 집니다.

즉, $KL$의 앞에 단순히 constant $\beta$ 를 곱하여 더 좋은 disentanglement를 얻을 수 있다는 것이 본 연구의 핵심입니다.

$\mathcal{D} = \{ X,V,W \}$ 라고 하겠습니다.
$x$는 real image이고 $v$는 conditionally independent factor이며 $w$는 conditionally dependent factor입니다.

쉽게 생각하면 real image $x$가 있으면 이에 대한 feature가 있는데 disentangled feature를 $v$, entangled feature를 $w$라고 합니다.

$p(x \mid z)$는 generator에서 나온 generated image가 real image일 확률인것을 기억해 봅시다.
이를 $v, w$로 다시 표현한다면 $p(x \mid v, w)$라고 표현할 수 있습니다.

Model은 $p(x \mid z)$를 maximize해야 하므로
$\displaystyle\min_\theta E_{P_\theta(Z)}\big( P_\theta(X \mid Z) \big)$가 objective function이 됩니다.

또한 $p(z)$를 $q_\phi(z \mid x)$로 대신 사용했었죠.

그럼 이제 $q_\phi(z \mid x)$에서 $v, w$를 분리해줘야 합니다.

이를 위해서 $p(z) \sim N(0, I)$로 해주면 됩니다.

이상하죠 VAE랑 완전히 같습니다. 하지만 VAE의 목적과는 완전히 다릅니다.

다시 짚고 넘어가자면 VAE는 Prior를 원하는 distribution으로 만들어 주기위해 $KL$을 추가했다면 여기서의 $KL$은 disentanglement를 하기 위해 넣어준다고 생각하면 됩니다. 흐름을 가져가지 위해 한가지 comment를 붙이면 다음과 같습니다.
VAE도 사실 Disentanglement가 된다. 원인은 $KL$이고, 본 연구에서 왜 되는지 분석하고 이 정도를 늘린다. 입니다.

Object Function을 정리하면 다음과 같습니다.

4.2 $\beta$

이때 $\beta$를 KKT multiplier라고 합니다.

결론은 lower bound (4)가 나온다는 것입니다.
그리고 여기에서의 $\beta$가 제목의 $\beta$이고 이는 Disentanglement를 조정하는 contant가 됩니다.

논문의 말을 그대로 가지고 오면
$\beta$의 값이 크면 $v$의 disentanglement representation이 더 잘 학습된다. 입니다.

4.3 Results

$\beta=250$ 입니다.

$\beta=20$ 입니다.
결과를 볼때 resolution을 보는 것이 아닙니다. Disentanglement가 잘 되었는지 봐야합니다.
(b), (c)는 어느정도 잘 되었습니다.
DC-IGN과 VAE는 (a) interpolation이 잘 안되는 것을 확인할 수 있습니다.

5.추가로 보면 좋은 논문 list

Understanding disentangling in β-VAE, Nips 2017

Isolating Sources of Disentanglement in Variational Autoencoders, Nips 2018

A Style-Based Generator Architecture for Generative Adversarial Networks, CVPR 2019

Disentangling by Factorising, ICML 2018

Adversarial Latent Autoencoders, CVPR 2020

Interpreting the Latent Space of GANs for Semantic Face Editing, CVPR 2020

Disentangled and Controllable Face Image Generation via 3D Imitative-Contrastive Learning, CVPR 2020