[8주차] Meta-learning problem statement, black-box meta-learning

본 파일은 동명의 CS330 의 2주차 강의의 필기 내용입니다.

출처가 적혀 있지 않은 이미지는 모두 강의 PPT에서 발췌하였습니다.

정리

이 강의는 메타 러닝의 기본적인 내용을 전반적으로 정리하는 강의입니다.

용어 정리

본격적인 메타 러닝 내용에 들어가기 전에 기본적인 용어와 수식을 정리해 보도록 하겠습니다.

Single-task Learning

먼저 우리가 지금 까지 알고 있는 일반적인 학습 방법인 Single-Task Learning (단일 태스크 학습) 입니다.

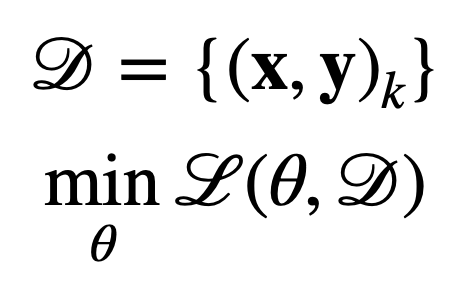
Single-Task Learning 은 주어진 데이터 분포 $D$ 가 존재할 때, 이 분포에서 손실 함수 $L$을 최소화 할 수 있는 파라미터 값 $\theta$ 를 찾는 것입니다.

이때 손실 함수는 우리가 알고 있는 함수 (크로스 엔토로피 등등) 을 포함합니다.

Task

Single-Task, Multi-Task 등등 태스크 라는 말을 많이 사용했는데 Task란 구체적으로 무엇일까요?

본 강의에서 Task는 다음과 같이 정의되어 있습니다.

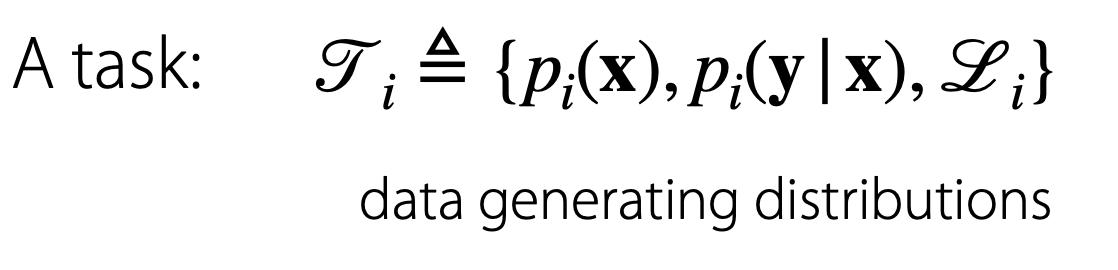
Task $T$ 는 입력 값 $X$ 에 대해서 입력값의 분포, 입력에 대한 출력값의 분포, 손실 함수 등을 사용하는 과정으로 생각할 수 있습니다.

본 문서에서 Task는 작성 및 의미 파악의 용이성을 위해 '과제' 또는 '태스크'로 병기하겠습니다.

Multi Task

Single Task와 Multi Task의 차이점이 무엇일까요

Single Task의 경우에는 하나의 목표를 수행하는 일반적인 과제입니다.

우리가 지금까지 공부했던 손글씨 인식(MNIST 등등)이나, 주어진 메일이 스팸인지 아닌지 분류하는 기술 등이 있었죠.

여기서 Multi-Task로 넘어가게 되면 분류를 수행하는 영역이 증가한다고 생각할 수 있을 것 같습니다.

앞 예시를 다중 과제로 변경하면 다국어 손글씨 탐지, 개인에게 특화된 스팸메일 탐지입니다.

두 과제 모두 손글씨가 무엇인지, 스팸메일인지 분류하는 것을 넘어서 비슷한 도메인 (국가별 차이, 개인별 차이)가 있는 모든 영역에서 작동하는 특징이 있습니다.

손실 함수

Multi-Task의 경우 손실함수는 기본적으로 모든 Task에 대해서 동일한 함수가 적용됩니다.

그럼 손실함수가 다른 경우가 있는 것일까요? 아래 두 상황일 때 해당됩니다.

• 분포가 달라서 하나의 손실을 적용하기 어려운 경우
• 하나의 Task를 다른 것 보다 더 중요하게 생각할 때

Task Descriptor

Multi-Task 학습의 경우에서는 다양한 과제별로 인공지능을 학습시켜야 하기 때문에 Task descriptor $z_i$ 를 사용합니다.

task descriptor의 상태에 따라 신경망이 다르게 작동한다고 생각될 수 있습니다.

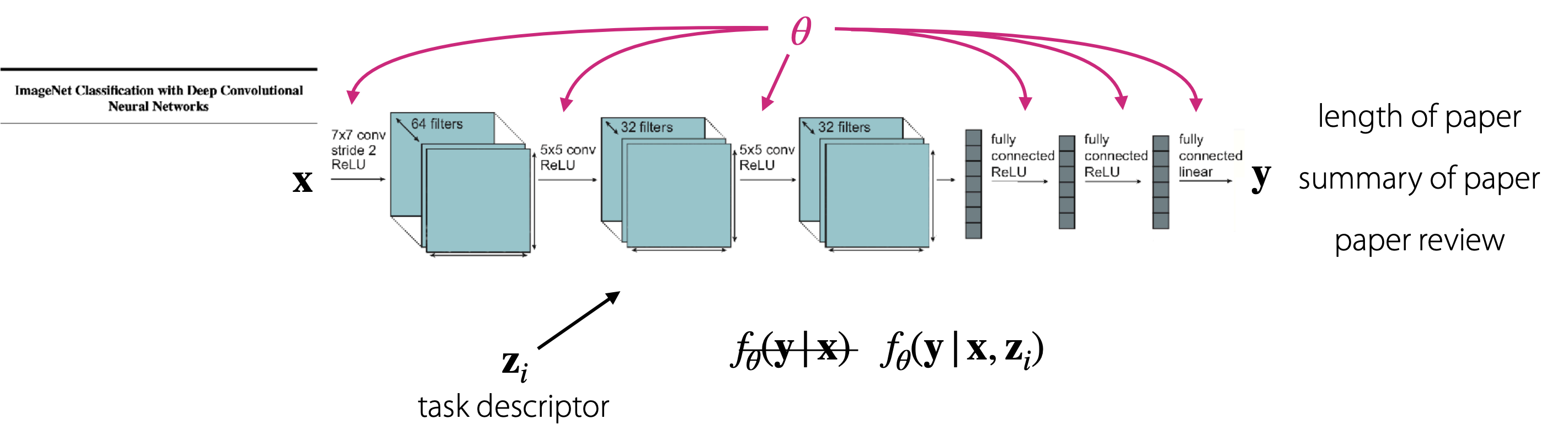
Task descriptor 는 각각의 과제를 구분하는 데 사용하기 때문에 과제별 특징을 명확하게 구분하는 데이터여야 합니다.

강의에서는 특징을 명확하게 구분하는 데이터를 세 가지로 제시했습니다.

• task번호의 원-핫 인코딩
• task의 메타 데이터
• task의 공식적 특징(formal specification)

손실 함수

task가 여러 가지가 있는 경우는, 목적함수는 Task들의 손실 함수의 합이 됩니다.

따라서 메타 러닝 문제에서 손실 함수는 다음과 같은 형태를 띄게 됩니다.

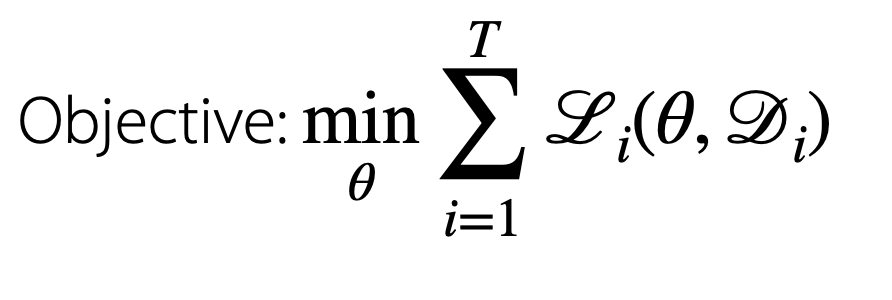
메타 러닝의 문제점

이 경우 두 가지 문제가 발생하는데

• Z의 조건을 어떻게 설정 (Task Conditioning)?
• 목적 함수를 어떻게 최적화 할까

태스크의 관리 (Task Conditioning)

태스크 관리는 각각의 과제에서 다루는 내용이 최소한으로 겹치게 구성하는 것을 핵심 내용으로 설정합니다.

이 방법에는 여러 가지가 있는데, 가장 먼저 생각나는 것은 네트워크를 피쳐별로 분할하는 것입니다.

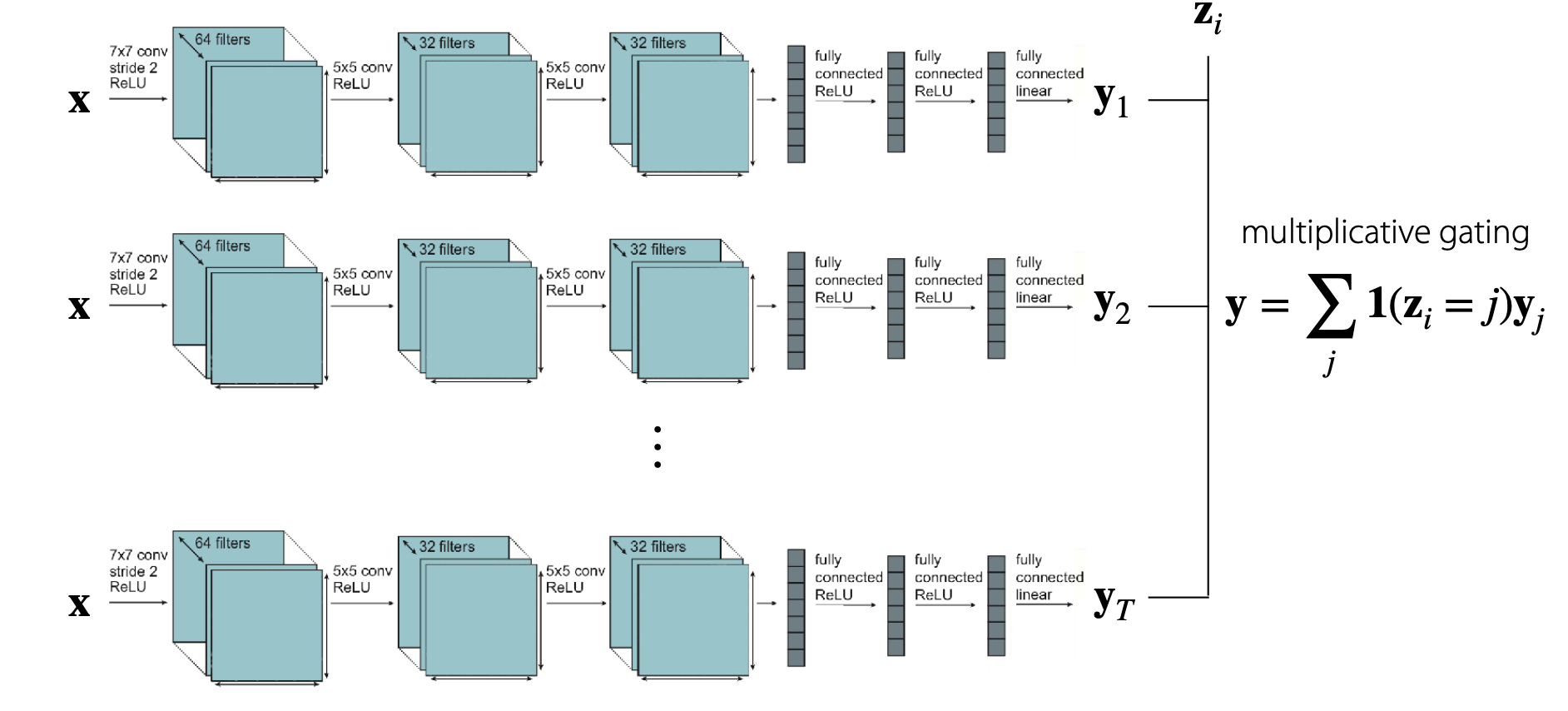
이 경우 각각의 네트워크는 파라미터를 공유하지 않은 채 여러 태스크로 관리되게 됩니다.

이로서 multiplicative gating이라는 효과를 얻을 수 있습니다.

또다른 방법으로로는 각각의 과제별로 입력값이나 활성화 값을 연결하여 하나의 네트워크로 취급하고 학습할 수 있습니다.

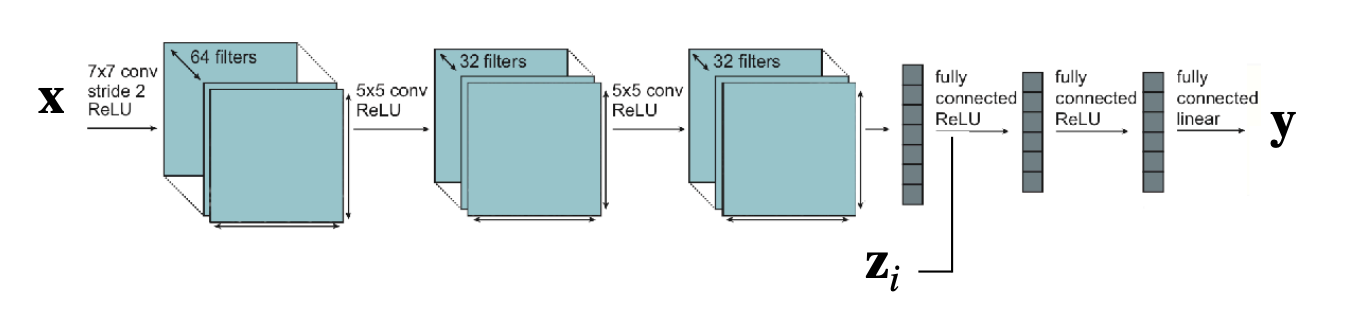
이 방법에서는 각각의 과제별로 공유하는 파라미터와 공유하지 않는 파라미터가 나뉘어집니다.

따라서 이 방법을 사용할 때의 목적 함수는 다음 식으로 나타낼 수 있습니다.

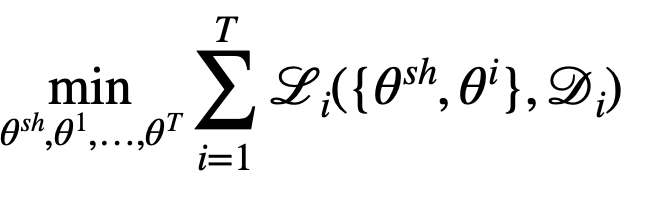
각각의 $\theta$는 과제별로 쪼개져 $\theta^1 ... \theta^i$ 가 되며 $\theta^{sh}$의 경우는 과제끼리 공유하는 공유 파라미터 입니다.

이 시각으로 볼 때 $z_i$를 설정하는 것은 과제 간 파라미터 공유를 어떻게 할 것인지를 결정하는 문제가 됩니다.

파라미터를 공유하는 Multi-task 문제의 구체적인 방법을 몇개 더 알아보겠습니다.

덧셈 구조

먼저 입력 값에 각 Task Descriminator를 연결 하거나 더해 주는 방법이 있을 수 있습니다.

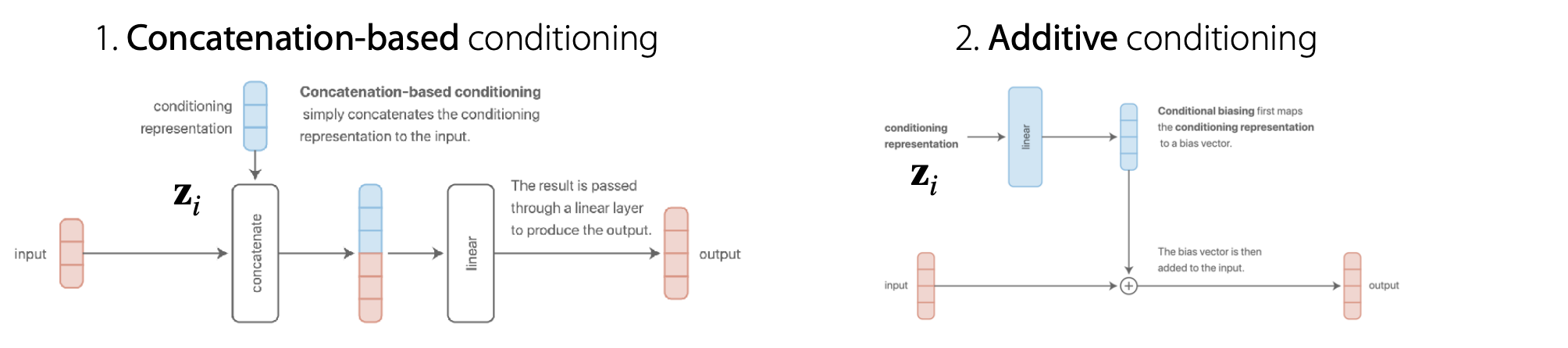
이 둘은 두 개의 기법처럼 보이지만 사실 같은 방법입니다. linear 층을 통과하는 과정에서 값이 하나로 합쳐져 계산되기 때문입니다.

멀티헤드 구조

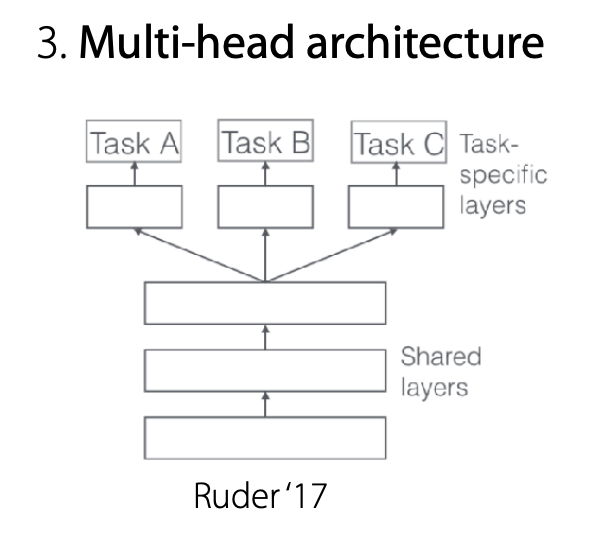
태스크가 각각 어떻게 공유되는지 특별히 지정된 것이 없는 경우 다음과 같은 방법을 사용할 수 있다고 합니다.

모델을 쪼개서 다양한 Head로 만들어 각각의 층을 통과하고 Shared Layers에 입력합니다.

곱셈적(Multiplicative) 구조

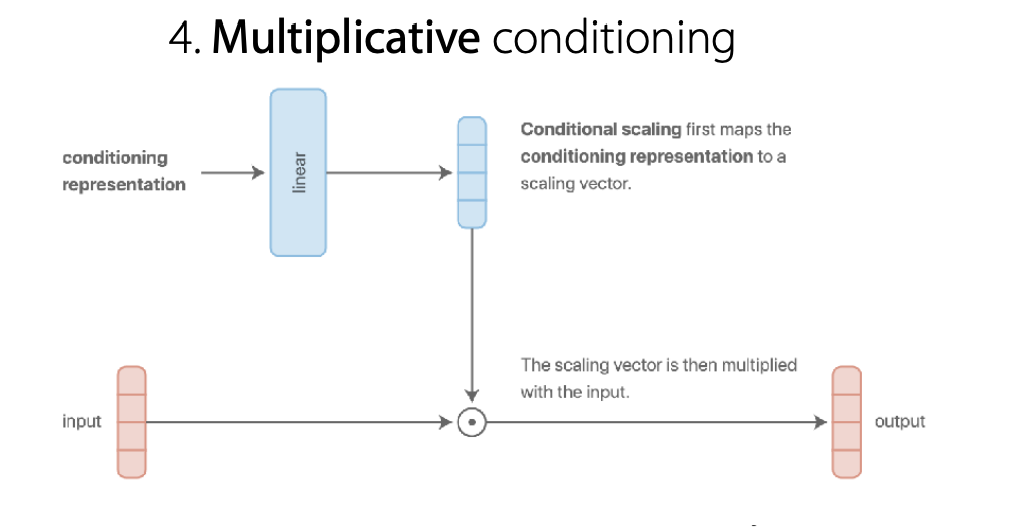
가장 흔한 방법 중 하나입니다. 덧셈적 구조에서 덧셈을 곱셈으로만 바꾼 구조입니다.

하지만 이 구조는 몇개의 이점을 가집니다.

• 덧셈적 구조보다 더 표현력이 있습니다.(Expressive)
• multiplicative gating의 특징을 얻을 수 있습니다. (각각의 특징을 모듈화하여 나눠서 계산할 수 있습니다.)

기타

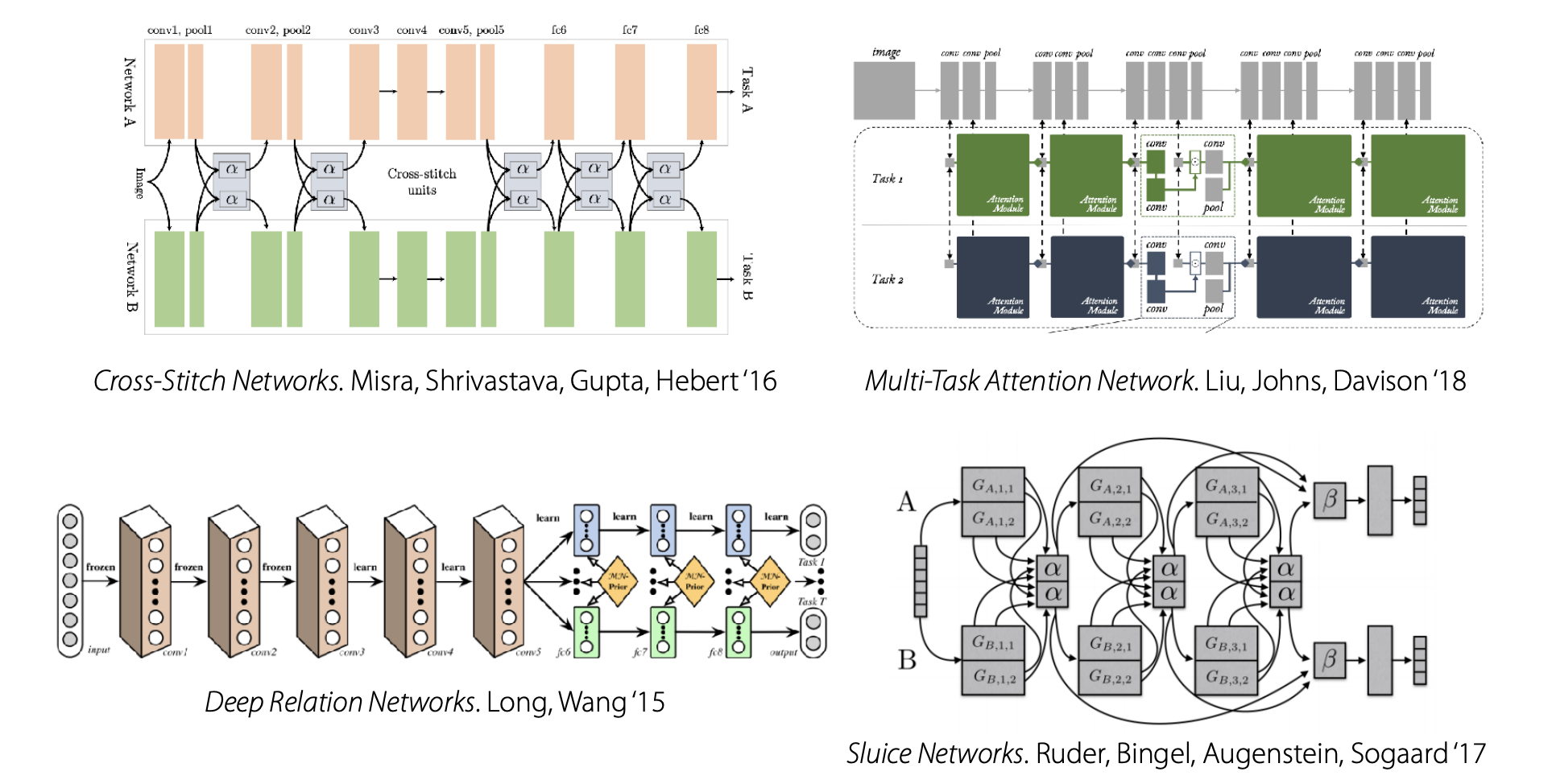
이 외에도 수많은 복잡한 알고리즘이 있지만, 시간 문제상 다루지 않았습니다.

선택법

그럼 이 구조들 중 어떤 구조를 선택하는게 좋을까요?

이 선택은 다음 특징을 가집니다

• 문제에 의해 결정
• 문제에 대해서 가진 직관과 배경지식
• 개인의 직관

목적 함수 최적화

목적 함수를 최적화 하는 것은 Single Task일 때와 별 차이가 없습니다.

• 과제의 미니배치를 구합니다.
• 미니배치에서 학습에 사용될 데이터를 샘플링합니다.
• 미니배치 별 손실값을 구합니다.
• 역전파를 통해 그래디언트를 구합니다.
• 구해진 그래디언트를 optimizer 알고리즘을 통해 학습시킵니다.

이 과정을 통해 미니배치를 구하고, 샘플링을 할 경우 데이터 양에 관계 없이 동등한 비율로 샘플링된다는 특징이 있습니다.

따라서 데이터의 양이 다른 경우 공정하게 샘플링될 수 있도록 조정해야 합니다.

어려운 점

Multi-task 학습을 진행할 때는 두 가지 어려운 점이 있습니다.

부정적 전이와, 오버피팅 문제입니다.

부정적 전이(Negative transfer)

다중 과제 방식으로 학습을 했음에도 불구하고 단일 모델이 성능이 더 좋은 경우를 이야기합니다.

하나의 태스크의 데이터가 다른 태스크에 영향을 주는 상황입니다.

CIFAR-100 데이터셋의 데이터로 확인해 본 결과 단일 모델이 성능이 가장 좋았습니다..

이 문제가 발생하는 원인이 무엇일까요?

첫 번째로 Optimization과정의 문제입니다. 각각의 과제 간 cross-task interference가 일어났거나, 과제가 다른 비율로 학습된 경우를 이야기합니다.

두 번째로는 파라미터나 Output이 모델의 표현 범위보다 부족한 경우 발생합니다.

Negative transfer를 해결하기 위해서는 태스크 간 공유되는 것을 줄여야 합니다.

Overfitting

앞 문제와 반대되는 내용으로 오버피팅을 들 수 있습니다.

각각의 과제를 아예 별개로 놓고 학습한 것으로 생각할 수 있습니다.

태스크 간 파라미터를 더 많이 공유하는 것으로 해결할 수 있습니다.

---

Meta-Learning Basics

본격적으로 메타 러닝에 대해서 알아보도록 하겠습니다.

메타 러닝 알고리즘은 크게 기계적 관점, 확률적 관점 두 가지로 나뉩니다.

기계적 알고리즘	확률적 알고리즘
- 알고리즘이 어떻게 실행되는지 알기 쉽다. - 데이터셋을 기반으로 새로운 데이터를 예측한다. - 메타 러닝 알고리즘을 적용하기 쉽다.	- 알고리즘이 무엇을 하고 있는지 알기 어렵다. - Prior information을 추출해서 효율적인 학습을 위해 조율한다. - 적은 양의 데이터에도 적용할 수 있습니다.

본 강의에서는 기계적 알고리즘은 다음 강의에서 설명한다고 하며, 확률적 알고리즘을 먼저 설명합니다.

확률적 알고리즘

확률적 알고리즘은 우리가 알고 있는 베이지안 알고리즘과 비슷합니다.

하지만 베이지안 알고리즘을 Multi-Task에 맞게 변형해 줄 필요가 있습니다.

기본적 지도학습

일반적인 지도학습 영역에서 출발합니다.

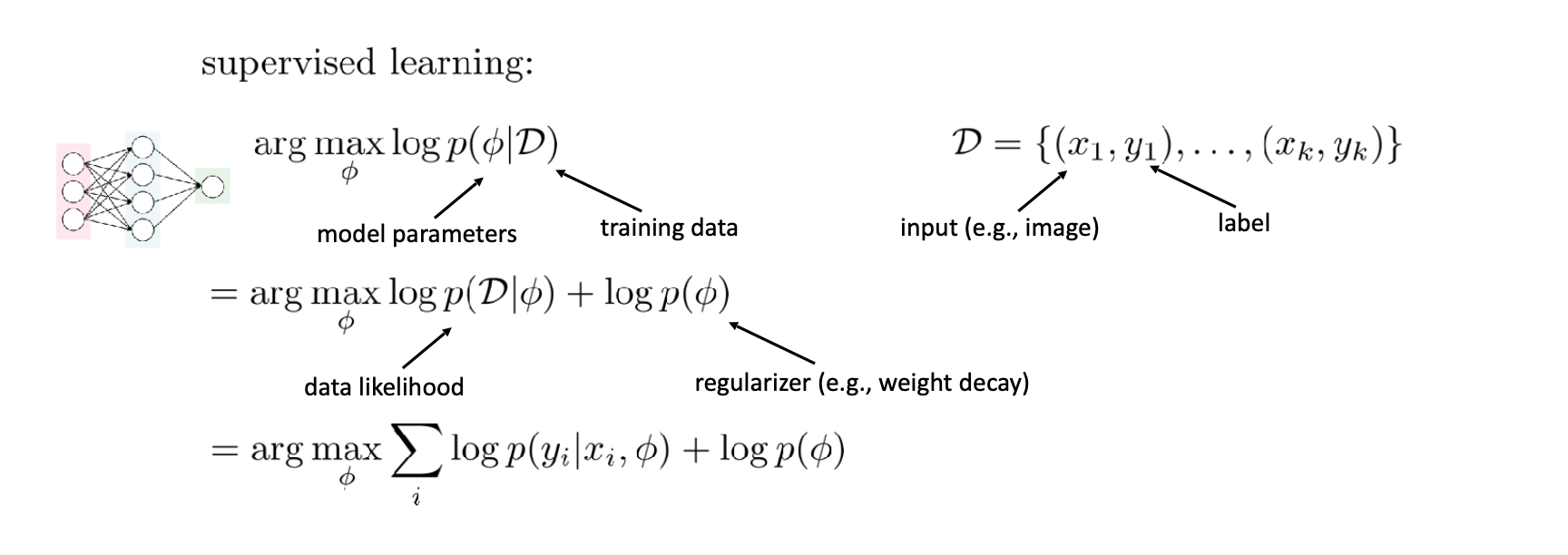
이 식에서 주로 확인해야 하는 것은 마지막 줄입니다.

$logp(y_i|x_i, \phi)$ 는 주어진 데이터 $x_i$와 파라미터 $\phi$ 에서 $y_i$ 가 나올 확률을 의미합니다. 이 확률을 최대화하는 작업이죠

하지만 이 방법은 데이터가 너무 적은 경우 오버피팅 문제가 생길 수 있습니다.

메타 학습 데이터

메타 러닝에서는 새로운 데이터를 효율적으로 반영하기 위해 '메타 학습 데이터'를 만들었습니다.

각각의 작업 별로 데이터를 따로 분할하여 이 전체의 집합을 메타 학습 데이터로 취급합니다.

만약 과거의 경험 $D_{meta-train}$을 남겨 놓지 않고 새로운 작업에 적용할 수 있는 능력만 배운다고 한다면, 메타-파라미터를 학습시켜야 합니다.

메타 파라미터는 $\theta : p(\theta|D_{meta-train})$로 정의되며, 주어진 태스크를 빠르게 해결하기 위해 $D_{meta-train}$에서 배워야 할 것을 의미합니다.

메타 학습 데이터를 활용한 Output의 분포는 다음 수식으로 나타낼 수 있습니다.

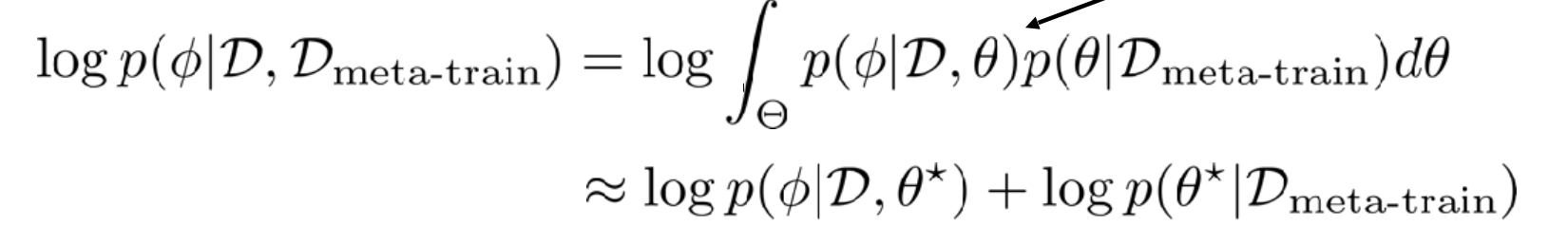
가장 마지막 수식을 주목해서 확인해야 합니다.

두 개의 항 중 왼쪽 항은 태크스 단일에서 학습되어야 할 파라미터이며, 오른쪽 항은 메타 러닝 과정에서 공통적으로 학습되는 파라미터입니다.

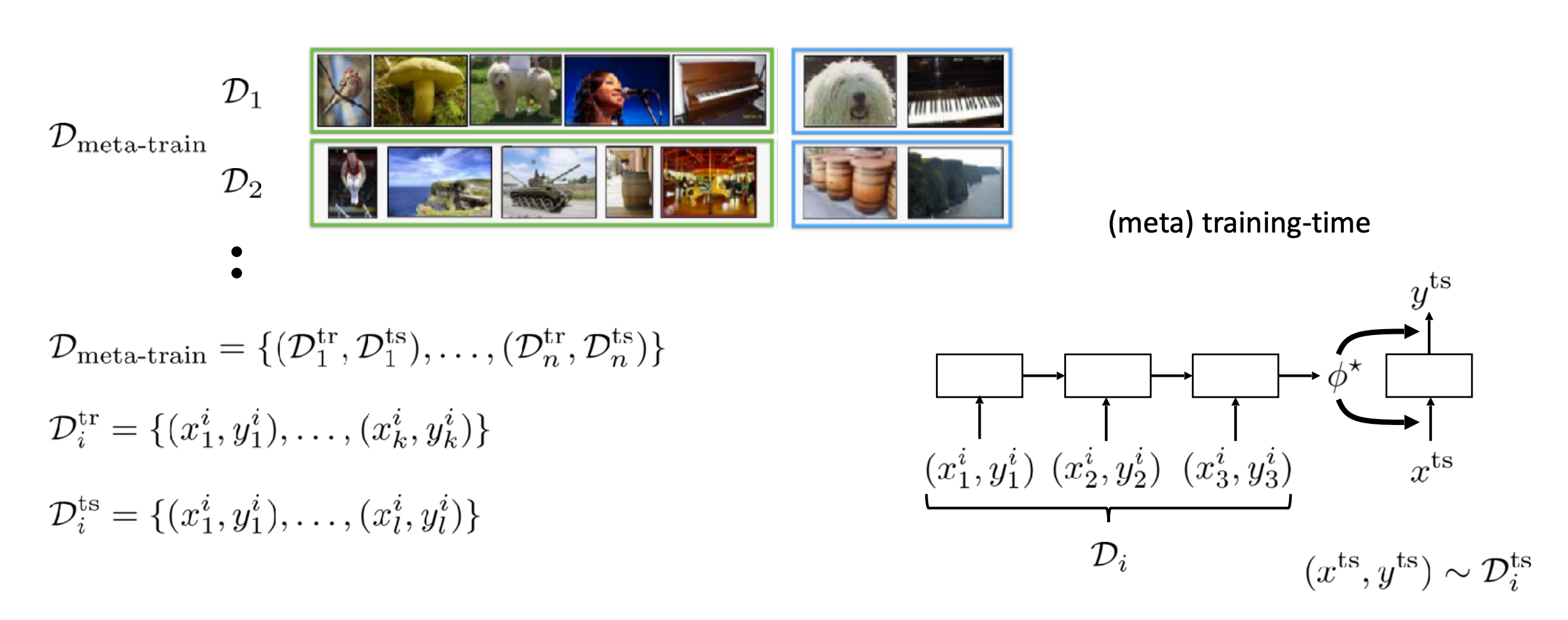
메타러닝 학습 과정

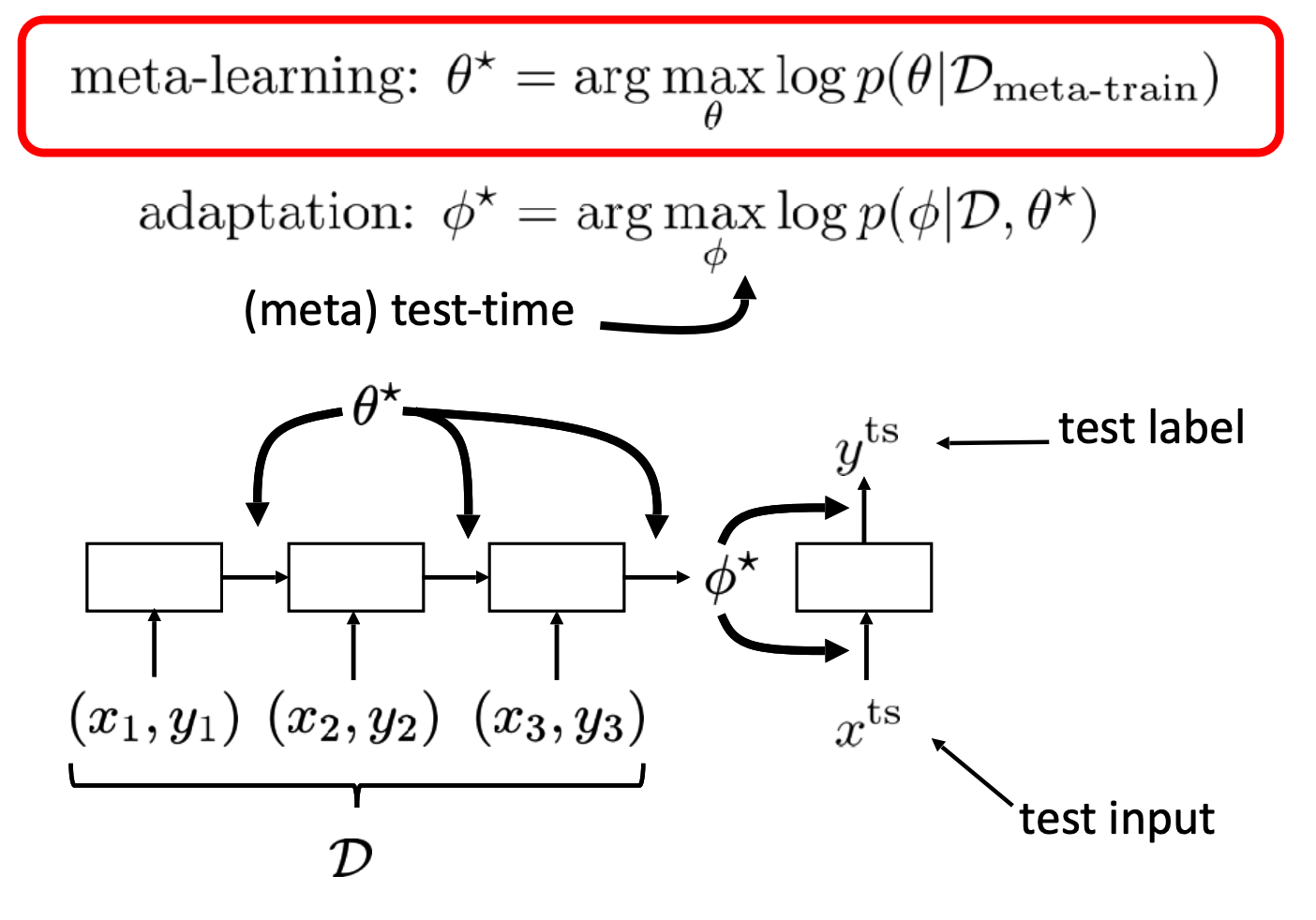
주어진 데이터셋 $D$에 대해서 메타 러닝 파라미터 $\theta\star$ 를 학습합니다. 이 과정을 메타 학습이라고 부릅니다.

이렇게 학습된 메타 러닝 파라미터를 가지고 테스트용 입력에서 출력이 나올 확률을 최대화 하는 $\phi\star$를 찾는 과정을 'meta testing' 이라고 부릅니다.

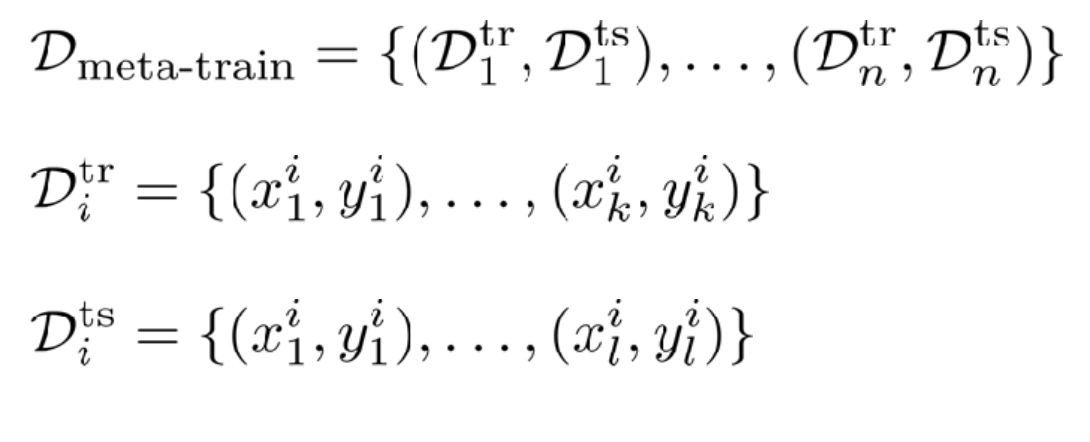
메타 트레인에 사용되는 데이터셋 $D_{meta-train}$의 경우는 $D^{tr}_i$ 와, $D^{ts}_i$ 로 구성됩니다. 전자는 $i$ 번째 태스크의 학습용 데이터, 후자는 테스트 데이터입니다.

즉 메타 학습은 $ \phi\star = f_{\theta\star}(D^{tr})$ 을 $D^{ts}_i$ 에 적합하게 만드는 과정이라고 볼 수 있습니다.

정리

위 내용을 한 번에 정리한 이미지가 강의 중에 나와서 소개해 보고자 합니다.

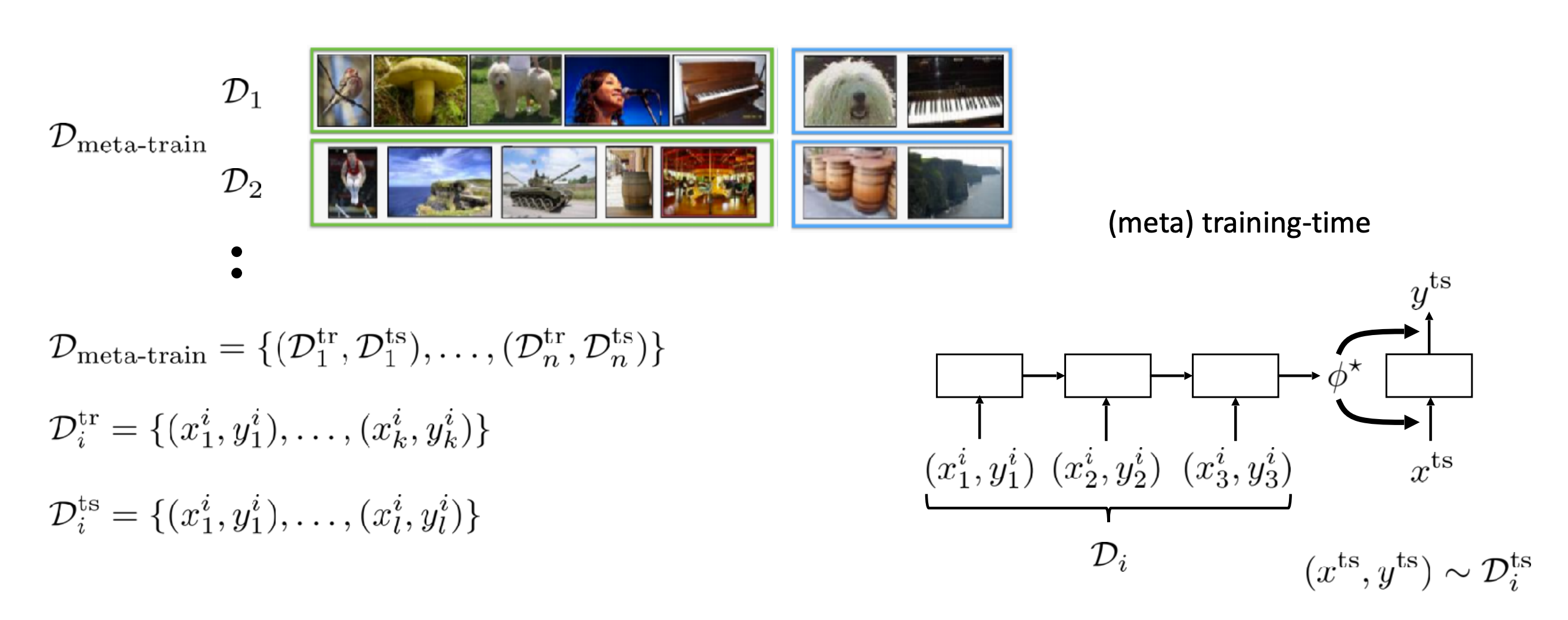
다른 적용 예시

이 구조는 Auto-ML이나 Architecture search에도 적용됩니다.

Auto-ML의 경우에서 $\theta$는 하이퍼 파라미터이고, 이를 통해 네트워크 가중치를 빠르게 학습시키는 것이므로 $\phi$ 는 네트워크 가중치입니다.

아키텍처 검색의 경우는 $\theta$ 는 네트워크 구조입니다. 적절한 $\theta$를 통해 빠르게 학습되는 네트워크 가중치를 찾는 것이므로 $\phi$는 네트워크 가중치입니다.

이 부분에 대한 연구도 매우 활발하게 이루어지고 있지만, 수업의 과정 이외 범위이기 때문에 다루지 않습니다.