[9주차] Optimization-Based Meta Learning

Meta-Learning

Problem

mnist dataset같은 경우, 적은 class에 다수의 데이터가 존재하기 때문에 각각의 class에 대하여 충분히 학습을 진행할 수 있었습니다. 하지만, omniglot dataset의 경우, 1623 cahracter(class)에 각각 20개의 instances밖에 존재하지 않습니다. 이러한 문제는 현실세계에서 다수 존재하며, few-shot discriminative & few-shot generative problems을 야기하였습니다.

Few-Shot Learning

여기서 5-way는 5 class를 의미하며, 1-shot은 각 class별 1개의 data를 의미합니다. 가지고 있는 데이터를 sampling을 진행하여 각각의 task에 할당하고, trainset, testset으로 나눠 학습시키는 구조입니다.

Meta Learning?

배우는 것을 위해 배우는 것으로, 학습 자체를 학습할 수 있는 능력을 키우는 것을 의미한다. 여기서 학습이란 여러 개의 경험이고, 경험들을 통해 학습의 Performance를 빠르게 향상 시킬 수 있게 된다.

인간의 경우, 강아지와 고양이를 구별하는데 많은 데이터가 요구되지 않으며, 이러한 특징들을 다양한 task에 대해서 AI모델에서도 반영하고자 하는 것이 meta learning의 학습방법이라고 말할 수 있습니다.

Supervised learning VS Meta learning

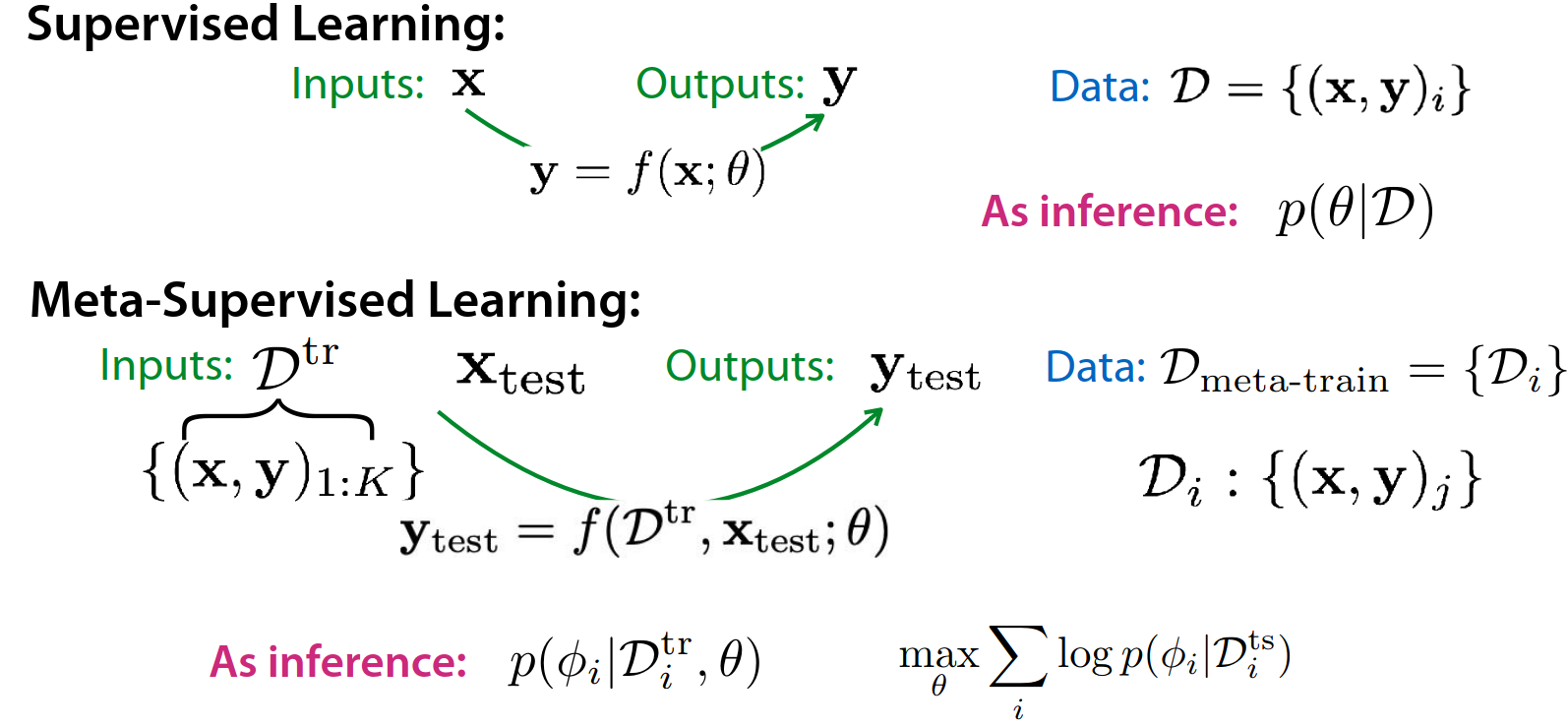
확률 관점에서 supervised learning과 meta learning의 차이점을 파악해보면 다음과 같습니다. supervised learning는 data $x$를 통해 output $y$를 도출하는 함수 $f$를 찾는 것이 목표이며, 이는 곧 데이터가 주어졌을 때, 확률을 높이는 $\displaystyle\theta$를 찾는 것과 동일하다고 말할 수 있습니다. 이에 반해 meta learning의 경우, 모든 task들의 확률을 높이는 meta parameter $\displaystyle\theta$를 찾는 것이라고 말할 수 있습니다. 직관적으로 봤을 대, task가 다르다하더라도, 모든 task들에 대해 모델을 적용했을 때, 가장 잘 설명할 수 있는 값을 찾는 것이라고 이해할 수 있을 것입니다.

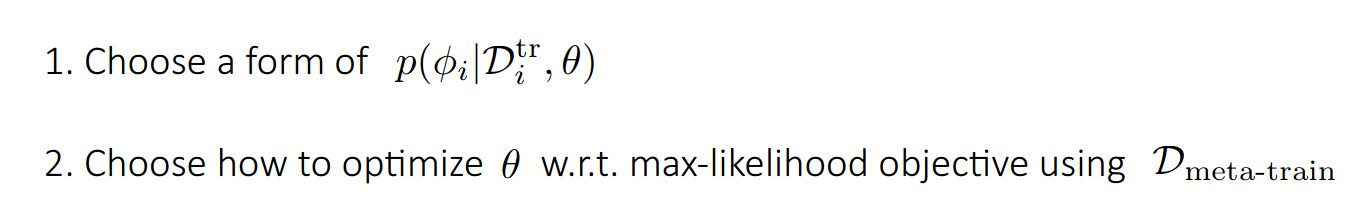
결국, meta learning의 학습 방법은 앞에서의 확률을 적용하는 것이라고 말할 수 있으며, 그러한 확률을 높이는 meta parameter $\displaystyle\theta$를 찾는 것이라고 말할 수 있습니다.

Recap:: Black-box meta learning

Black-box meta learning adaption

Black-box meta learning의 알고리즘을 간단히 살펴보면 다음과 같습니다.

1. 여러개의 task들을 생성하고, sample dataset를 구축한다.
2. 구축된 task들에서 train set과 test set으로 나눈다.
3. 주어진 i번째 train set을 통해 $\displaystyle\pi$를 계산한다.
4. 계산을 통해 구해진 $\displaystyle\pi$를 통해 test set에서의 Loss를 연산하면서 $\displaystyle\theta$를 update한다.

주목해야할 점은 $\displaystyle\pi$는 연산 과정에서 update되지 않으며, 오직 meta learning의 parameter인 $\displaystyle\theta$가 학습을 통해 update된다는 것입니다.

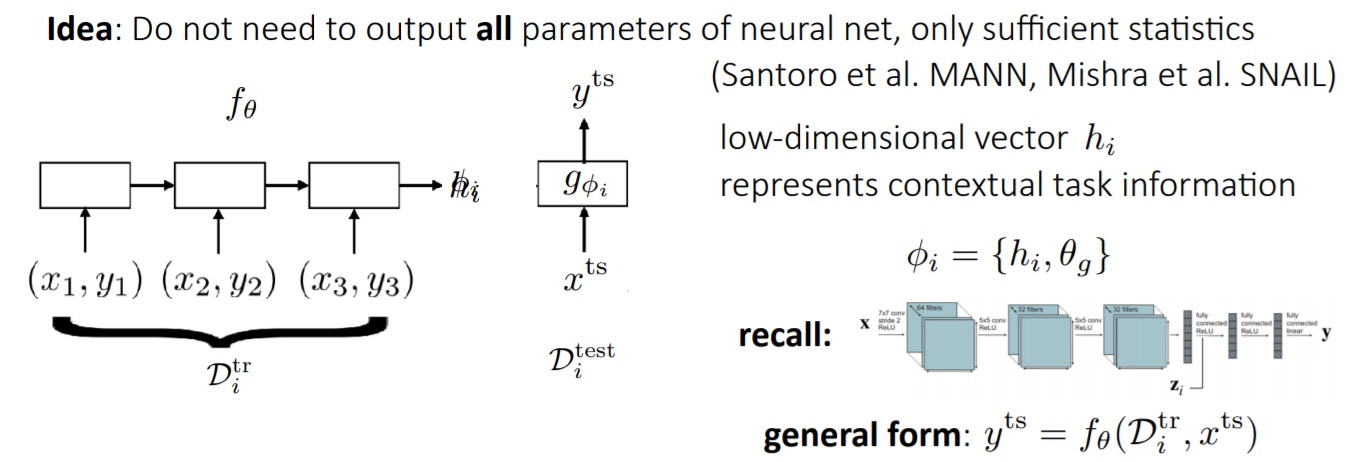
모든 parameter들을 저장하는 것보다, 충분한 정보만을 기억해두는 것이 좀 더 효과적이라고 말할 수 있을 것입니다. 기존의 파라미터 $\displaystyle\pi$를 output으로 도출하는 것보다 task의 정보들을 응축한 저차원의 $h_i$ vector를 output으로 도출합니다. 이는 이전 강의에서 다뤘던, multi task에서 task에 따라 다른 task information을 summmation하는 방법과 유사하다고 볼 수 있습니다.

이러한 black-box meta learning의 경우, expressive (다양한 function 적용가능) & easy to combine with variety of learning problems (e.g. SL, RL)한 장점을 가지고 있습니다.

하지만, 다양한 데이터를 훈련하고, 다양한 테스트 셋에 대한 예측을 진행한다는 측면에서 complex model & complex task의 문제가 발생할 수 있습니다. 직관적으로, meta task들에 대한 학습을 진행하는데 optimization procedure이 무척이나 힘들 것으로 예상됩니다.이러한 이유들 때문에 데이터의 불충분한 현상이 발생하여 model이 잘 학습하지 못하는 경우가 때때로 발생하기도 합니다.

Optimization-Based Inference

기본적인 아이디어는 기존의 meta-parameter를 사전정보로 활용하는 것입니다. 쉽게 설명하자면, meta-parameter $\displaystyle\theta$를 fine-tunin의 initialization으로 사용하겠다는 것입니다.

기존의 task parameter를 업데이트 하는 과정에서 pre-tranined parameter를 가져와서 각각의 task에 맞게 fine-tuning을 하여 optimization하는 것으로 이해할 수 있습니다. 해당 방식에서의 목적은 적은 update만으로 $\displaystyle\pi$를 구할 수 있는 $\displaystyle\theta$를 찾겠다는 것입니다.

pretrained parameter는 vision분야에서는 imageNet classification에서의 parameter, NLP분야에서는 bert의 parameter 등 다양한 공개된 parameter들이 많기 때문에, 이를 가져와서 사용하면 된다고 말합니다.

Optimization-Based Meta Learning Algorithm

본 자료는 DMQA seminar의 발표자료를 활용했음을 미리 알려드립니다.

먼저, pretrained된 parameter $\displaystyle\theta$를 사용하여 trainset를 활용하여 학습한 후에, 그에 맞는 $\displaystyle\pi$를 찾습니다. 그런 다음 testset를 활용하여, 각각의 task의 정보들을 종합하여, 최적의 meta parameter $\displaystyle\theta$를 도출하는 것입니다.

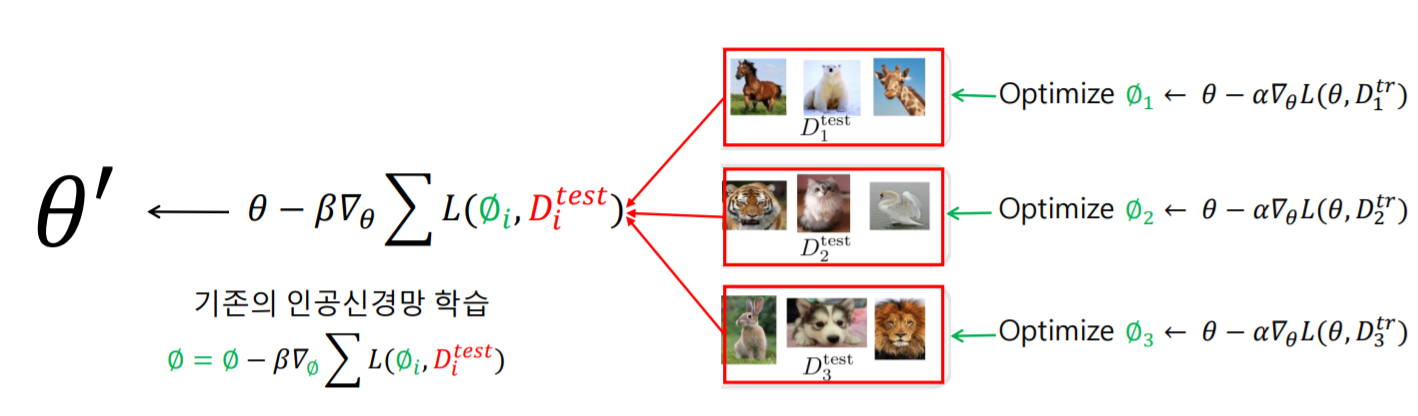
이러한 방식을 반복하면서 meta-learning의 학습이 진행된다고 생각하시면 됩니다.

앞에서의 black-box adaption 방식과의 진행방식의 차이를 보면 다음과 같습니다.

위의 가정들을 만족할 때, black-box 접근방식을 통해 얻을 수 있는 representation의 특징을 optimization-based meta learning인 MAML에서도 찾아볼 수 있다고 말하고 있습니다.

Results

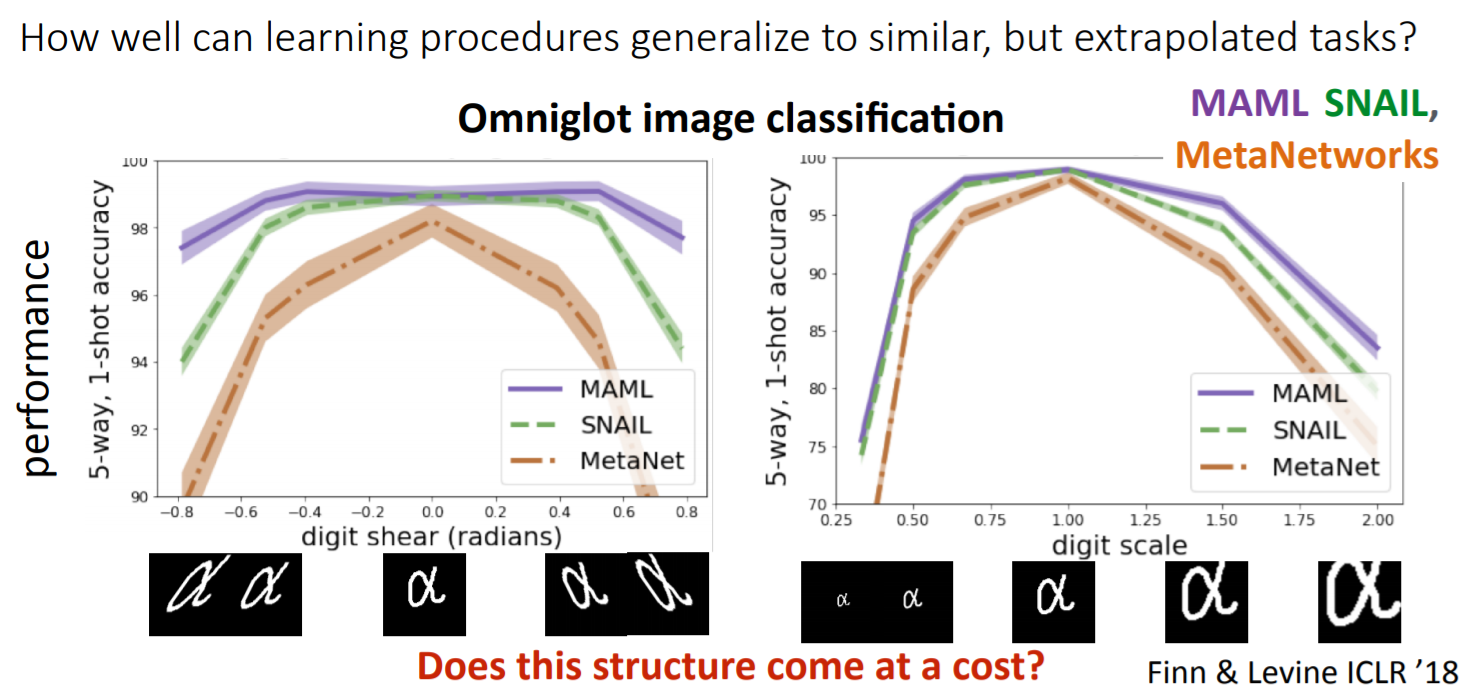
Omniglot dataset의 경우, 1623개의 chracters(class)가 있지만, class의 example은 20개의 데이터만을 가지고 있습니다. 해당 데이터를 5way-1shot 개념을 활용하여 글자의 돌려진 정도, scale한 정도에도 변함없이 다른 모델들에 비해 좋은 성능을 보이는 것을 볼 수 있습니다.

참고자료
http://cs330.stanford.edu/fall2019
http://dmqm.korea.ac.kr/activity/seminar/265