5. Label Propagation for Node Classification

작성자 : 권오현
0. Intro
Main Question : 몇몇의 Nodes에 Label이 주어진 Network(Graph)에서 다른 Nodes의 Label을 어떻게 할당할 것인가 ?
-
Lecture 3에서 배운 Node Embeddings에 Simply Classifier (Which node is trusted or not trusted )를 추가하면 해결된다.
-
이번 Session에서는
Semi-Supervised Node Classification의 방법으로 해결해 본다. -
Semi-Supervised Node Classification : 주어진 nodes의 labels을 통해 unlabeled nodes의 label을 예측
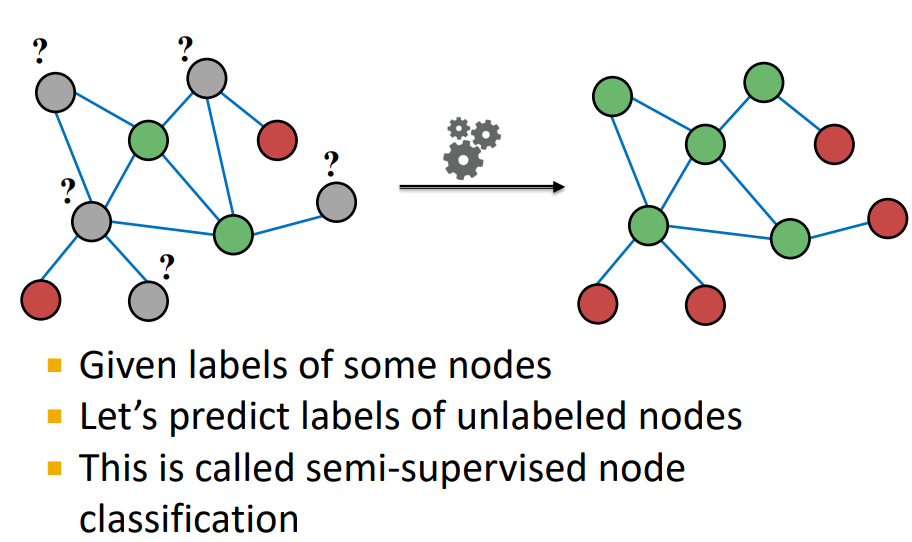
cf. Semi-Supervised Learning :
Label이 있는 데이터를 학습 하는 Supervised Learning과 Label이 달려 있지 않는 데이터를 학습 하는Unsupervised learning 의 조합으로 이루어진 것을 의미한다.
1. Collective Classification
Intuition : Correlations exist in networks
-
Network에서 동일한 Label을 가지는 Nodes는 연결되어 있다고 생각한다. (Network 상에는 Correlation이 존재한다.)
이러한 가정을 통해 유사한 Nodes는 군집을 형성하고 있다고 판단.-
Semi-Supervised Learning -
Labels of the neighbors in the network의 정보를 통해 우리가 예측해야할 node v에 Label을 assign 해준다.
-
Collective Classification Techniques :
- Relational Classification
- Iterative Classification
- Belief Propagation
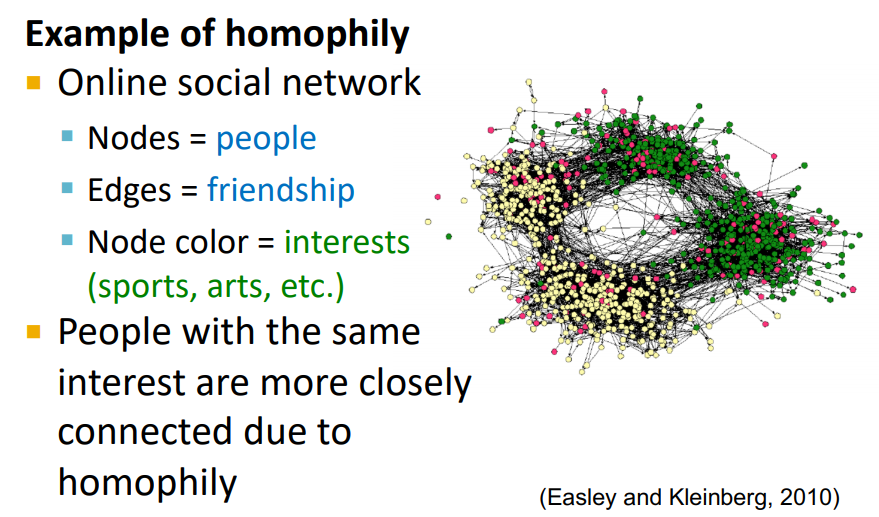
Correlations Exist in Networks
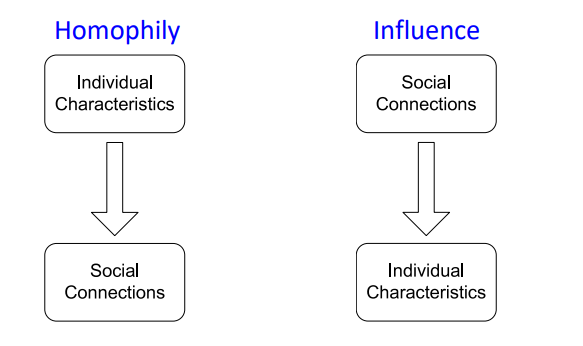
- Homophily
"The tendency of individuals to associate or bond with similar others "- Birds of feather flock together (유유상종)
- 비슷한 관심사를 가지는 경우 connection이 형성된다.
- Influence
"Social connection can influence the indivisual"
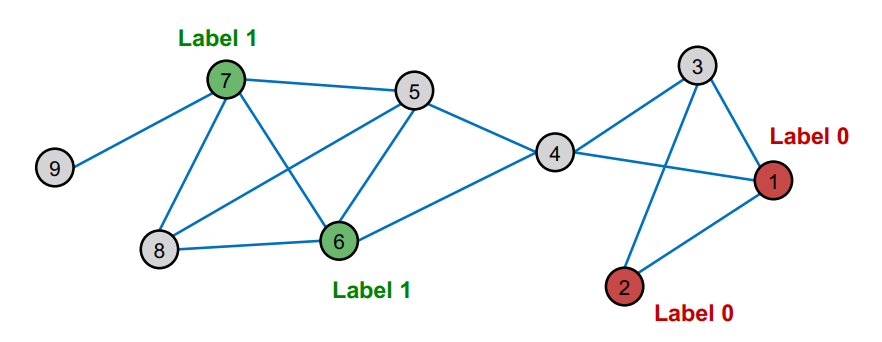
Question : How do we leverage this correlation observed in networks to help predict node labels ?
-
Motivation
-
유사한 nodes은 일반적으로 Close together 이거나 Directly connected 되어 있다.
guilt-by-association : 내가 label이 x인 노드와 연결되어 있으면 나도 label이 x일 확률이 높아진다 !
-
네트워크 내에서 node v의 Classification label은 다음 3가지에 의해 영향을 받는다.

→ 이제 networks에 homophily이 존재한다고 가정하고 graphically하게 생각해 보면 같은 label의 nodes가 서로 연결되는 경향이 있다!

-
-
결론적으로 Node classification task는 unlabeled nodes가 Class 1이거나 Class 0인 확률을 예측하는 것이다.
- A : Adjaceny matrix, A는 unweighted or weighted / undirected or directed
ex) Document classification, Link Prediction, Spam and fraud detection 등
Collective Classification Overview
Intuition : Simultaneous classification of interlinked nodes using correlations
-
Probabilistic Framework
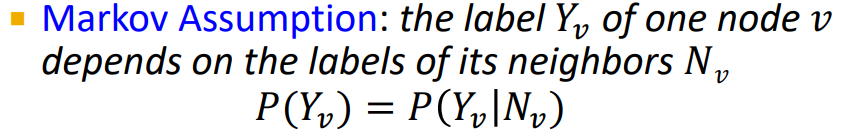
- label 는 neighbor nodes 의 label에 의존한다. (degree 1 neighborhood)
: 어떤 확률변수 의 분포는 바로 직전에 나타난 확률 변수 에만 의존한다. 이 부터 까지의 정보도 포함하고 있다고 가정
- label 는 neighbor nodes 의 label에 의존한다. (degree 1 neighborhood)
-
Collective Classification은 "altogether classifying all the nodes on the graph because every nodes labeled depends on other nodes labeled"
→ nodes will be update the belief for a prediction about the labels until the process will converage
-
STEP 3
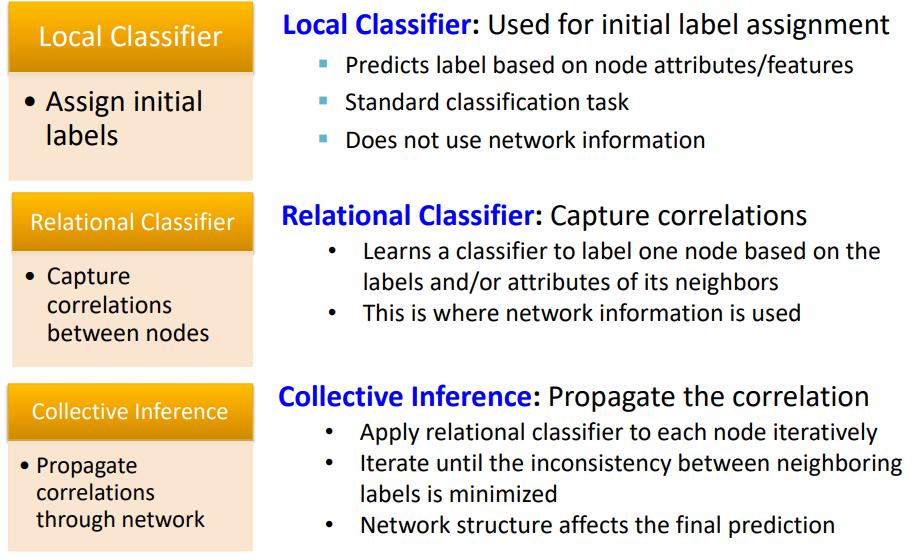
- STEP 1 :
Local Classifier- node의 attributes/features를 통해 초기 Label을 할당한다.
- 이 때 network information은 사용하지 않는다.
- STEP 2 :
Relational Classifier- nodes간의 correlations를 capture 한다.
- neighbors의 label/attribution 정보를 사용하여 classifier를 학습한다. (여러번 반복)
- STEP 3 :
Collective Inference- Propagate the correlation
- 각 nodes 마다 Relational Classifier를 수행한다.
- 결과적으로 network의 정보를 사용하여 nodes의 label을 예측한다.
- STEP 1 :
→ Collective Classification은 neighborhoods의 labels의 inconsistency가 최소화 될 때 까지 반복한다.
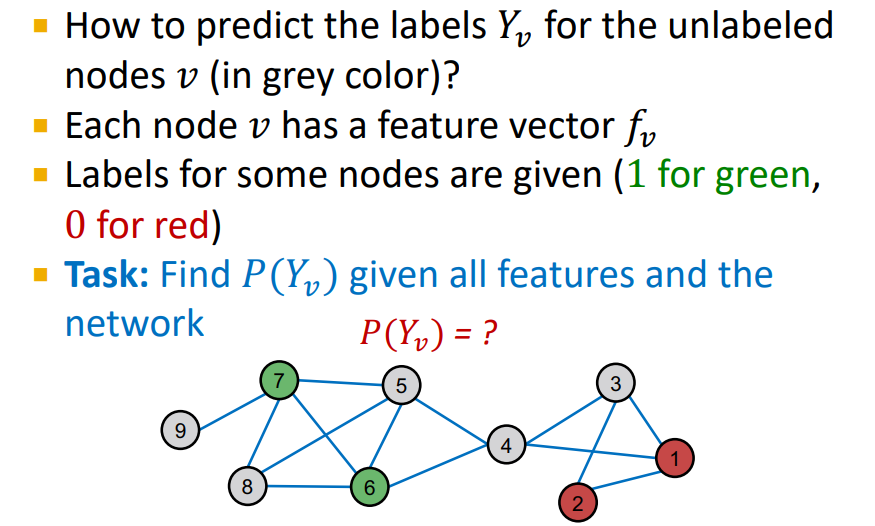
2. Relational classifiers
Setting
-
Basic Idea : node 의 의 class probability는 neighbors의 class probability의 weighted average
-
labeled node : ground-truth label 로 initialize
-
unlabeled node : 를 uniform하게 initialize, 믿을만한 prior가 존재하면 이를 사용하여 initialize
-
update : 수렴 or max iteration 까지 모든 노드를 random order로 업데이트 한다.
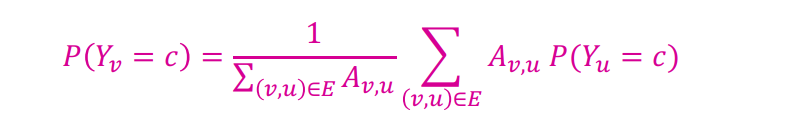
- : node v의 counts the degree or the in-degree of node v (만약 edges가 weight information이면 는 node v, u 사이의 edge weight)
- : edges의 weight * neighbor의 label = c 일 likelihood
- : node v의 label = c일 likelihood 이기 때문에 normalization을 위한 계수
Example
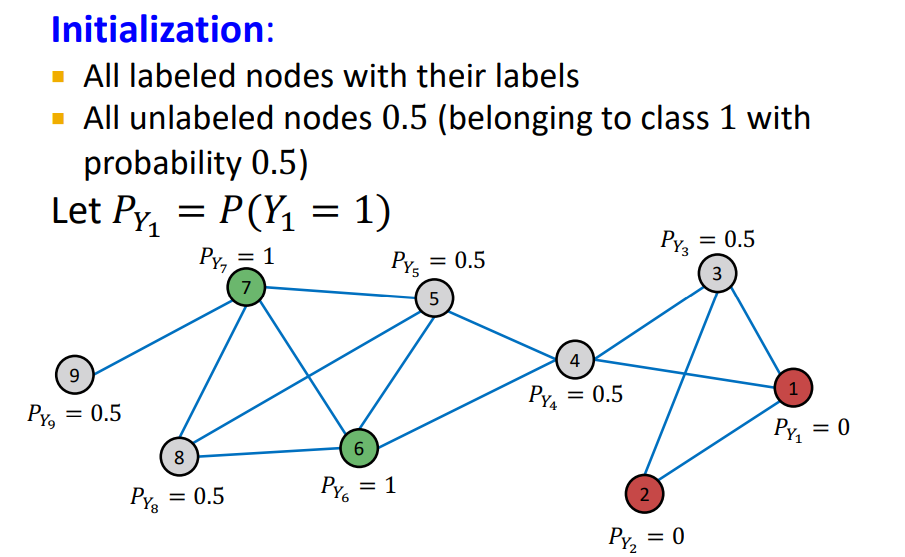
- Initialize : labeled nodes 는 groud-truth에 맞게 초기값을 설정, unlabeled nodes는 0.5로 설정
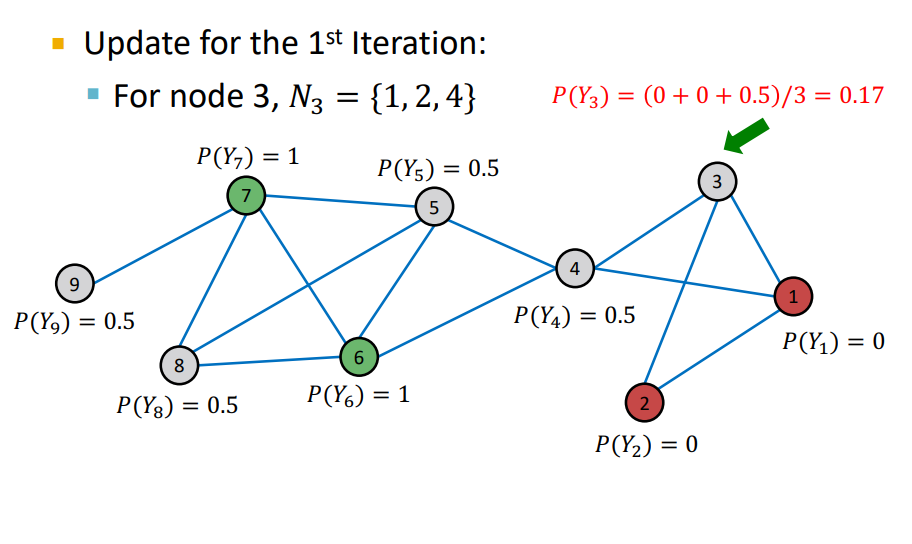
- Iteration : random order를 통해 unlabeled nodes의 probability를 update
- unweighted graph 이기 때문에 neighbors의 average로 설정
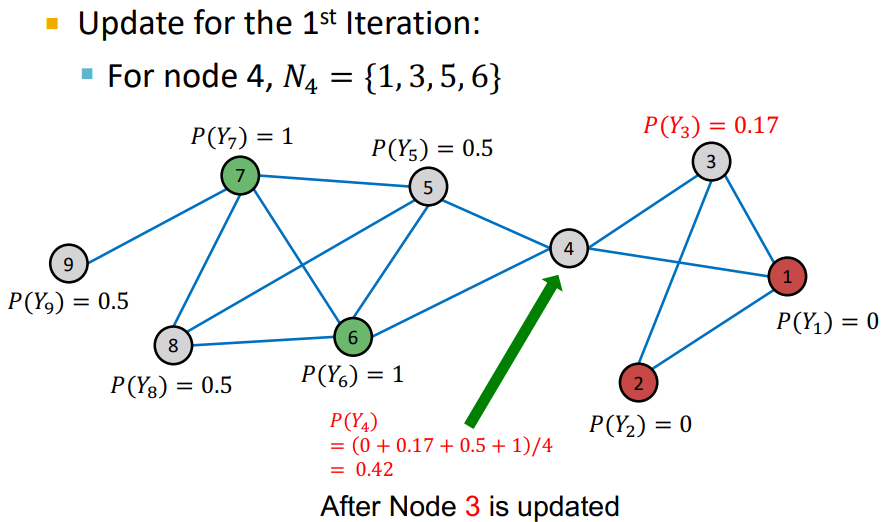
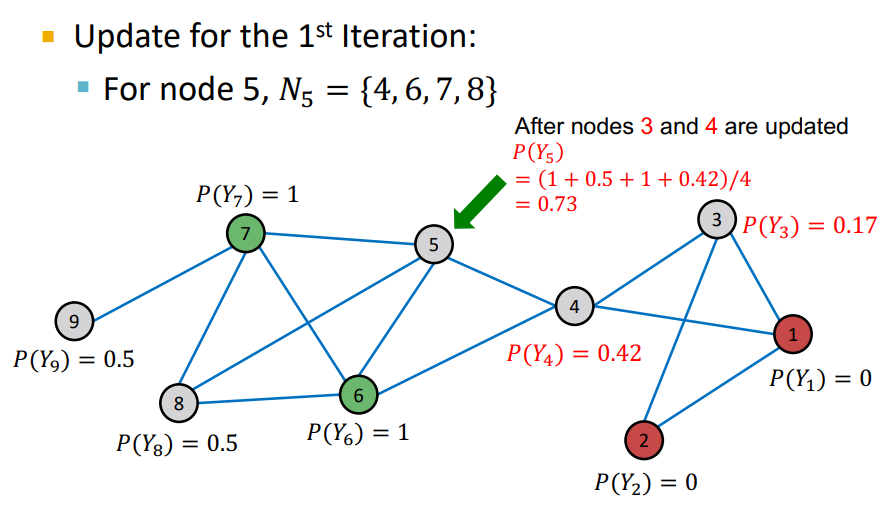
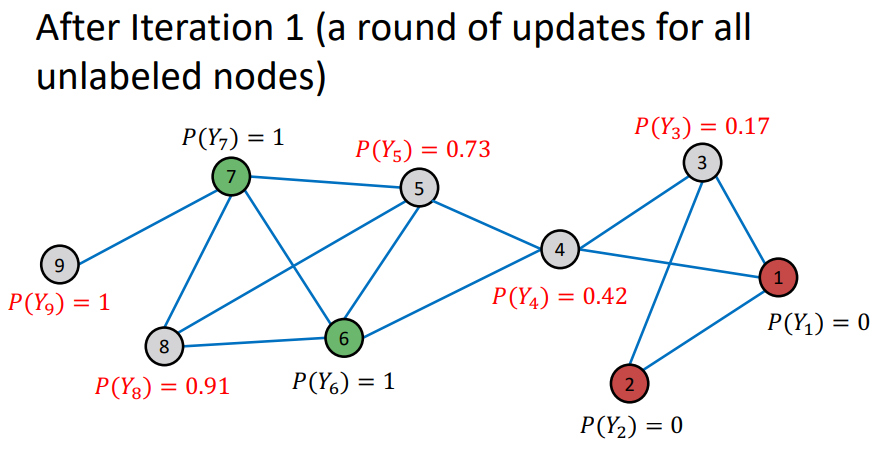
- node의 probability가 update 됨
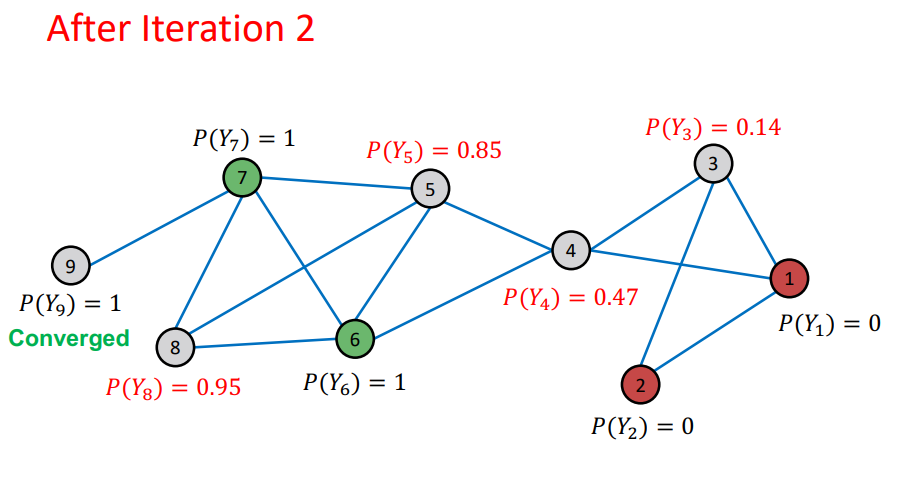
- Repeat Iteration : 모든 node가 수렴되거나 max iteration 까지 반복
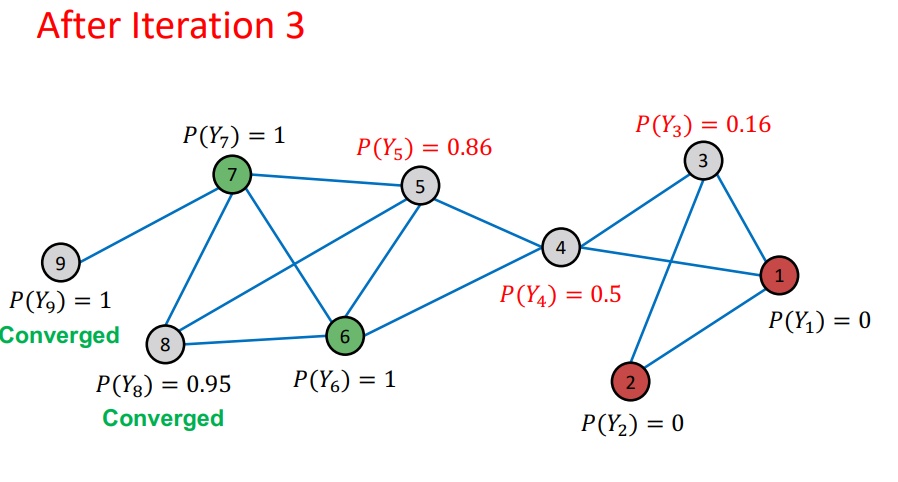
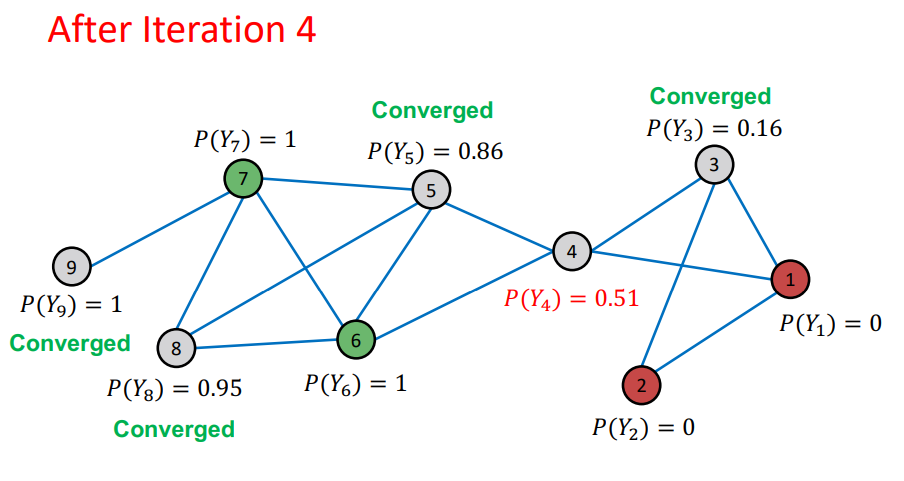
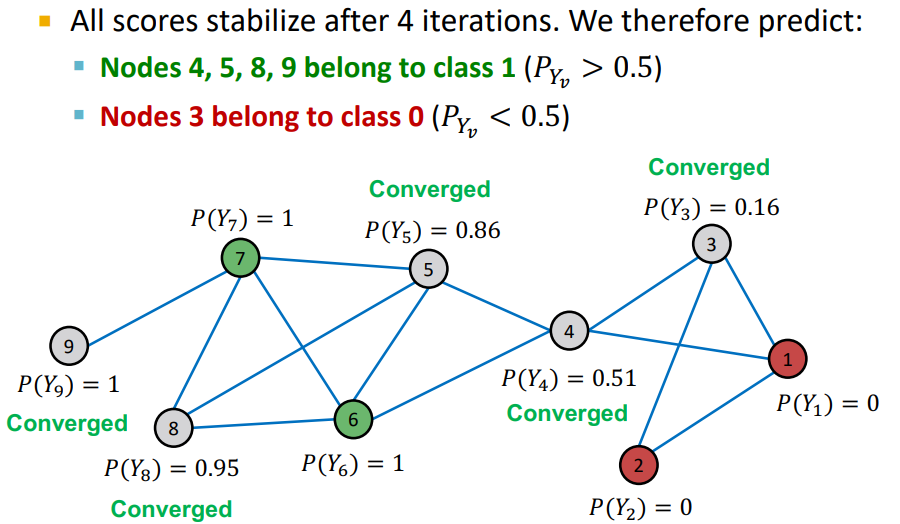
- 여기에서 이전 Iteration과 다음 Iteration에 대해서 node의 probability가 변하지 않으면 수렴 되었다고 판단
- random order 로 학습이 되기 때문에 이전 node의 probability가 다음 node의 probability에 영향을 미치기 때문에 Propagate
Challenges
- 수렴이 보장되지 않는다.
- node의 feature information을 사용하지 않았다.
→ 단순히 nodes의 label과 network information만 이용하기 때문이다.
3. Iterative Classification
Setting
-
Main Idea : 단순히 neighbor set 의 labels 만 사용한 Relational Classifier 방법에 neighbor set 의 attributes 도 사용
-
Input : Graph
- : feature vector for node
- : labeled nodes
-
Two Classifiers
- : feature vector 를 통해 node label을 예측하는 모델
- : feature information과 network information(summary of labels of 's neighbors) 두개 다 고려하여 node label을 예측하는 모델
Compute summary of labels of 's neighbors :
- Histogram of the number of each label in
- Most common label in
- Number of different labels in
-
Update :
-
Iterative classifier는 2step으로 구분된다.

-
Phase 1 : training set을 통해 classifier를 학습한다 e.g., linear classifier, svm, neural networks
- : node의 feature 를 통해 node의 label 를 예측하는 모델
- : node의 feature , summary of labels of 's neighbors 를 통해 node의 label 를 예측하는 모델
-
Phase 2 :
- 를 통해 node의 label 를 할당
- summary of labels of neighbors를 compute
- , 를 이용하여 모델()을 통하여 labels를 예측한다.
- Repeat for each node v
- Update based on
- Update based on the new ()
- 수렴하거나 max iteration 까지 반복 !
- Convergence is not guaranteed
-
Example : Web Page Classification
- input : Graph of web pages
- Node : Web page
- Edge : Hyper-link between web pages (Directed edge)
- Node features : Webpage description
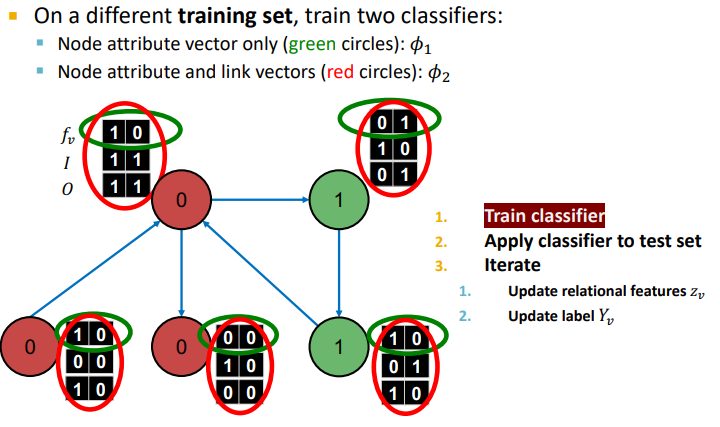
-
Phase 1 :
-
: feature vector 를 통해 node label을 예측하는 모델
-
: feature information과 network information(summary of labels of 's neighbors) 두개 다 고려하여 node label을 예측하는 모델
위의 그래프 경우 Directed graph이기 때문에 Incoming neighbor label information, Outgoing neighbor label information vectorfmf 고려해야 한다.
- : Incoming neighbor label information vector
- : Outgoing neighbor label information vecotr
- : 최소 1개의 Incoming node의 label이 0 이면 1 아니면 0
- : 최소 1개의 Outgoing node의 label이 0 이면 1 아니면 0
-
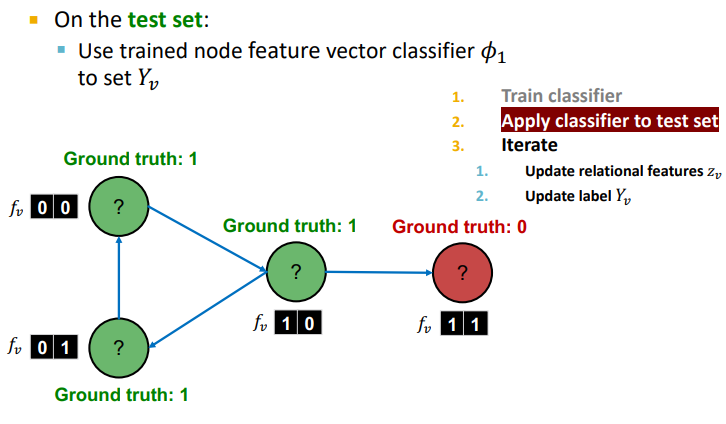
2. Phase 2 : 위에서 학습한 , 를 Test Set에 적용해보자 !
-
node feautre 를 사용한 모델 를 통해 할당
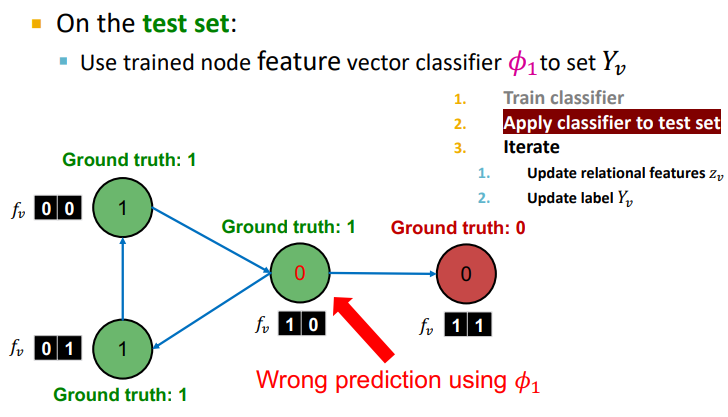
-
할당된 를 통해 summary of labels of 's neighbors compute
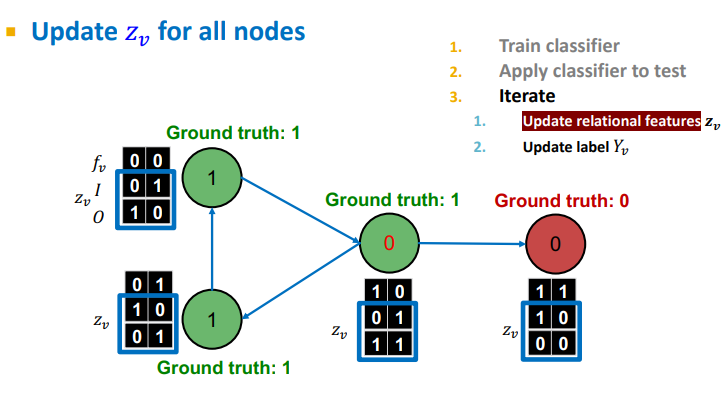
-
와 를 이용하여 모델 를 통해 update
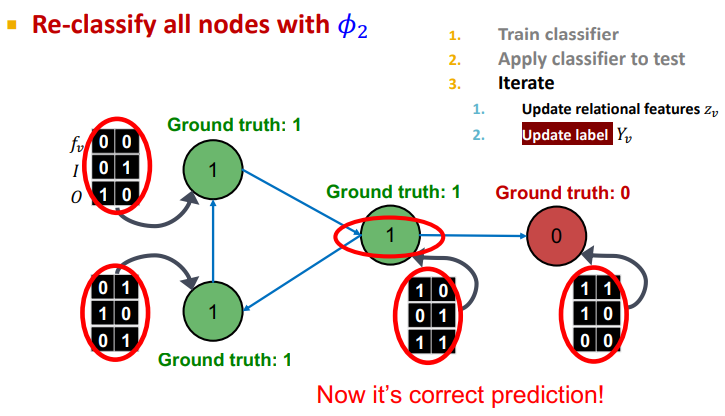
-
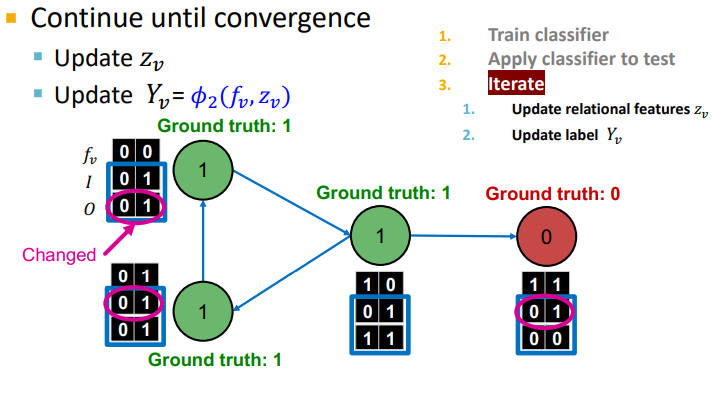
수렴이나 max iterations 까지 반복
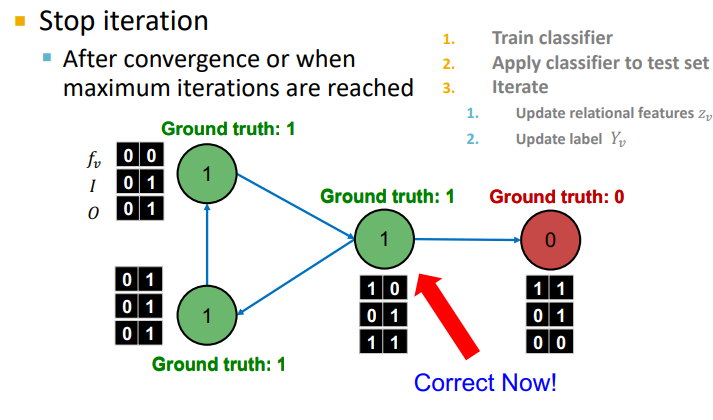
Summary
- Relational classification : Iteratively update probabilities of node belonging to a label class based on its neighbors
- Iterative classification :
- Improve over collective classification to handle attribute/feature information
- Classify node based on its features as well as labels of neighbors
4. Belief Propagation
Setting
-
Main Idea :
-
Graph에서 조건부확률 queries에 대한 Dynamic Programing approach
-
Neighbors가 서로 'Talk'하는 Iterative Process,
Passing Messages -
"When consensus is reached, calculate final belief"

Belief Propagation(신뢰전파 알고리즘) : Graphical Model에서 일부 노드에 대한 확률 분포 또는 값이 주어졌을 때, 다른 노드에 해당하는 확률 변수의 분포를 추정하는 문제 !
-
Message Passing : Basics
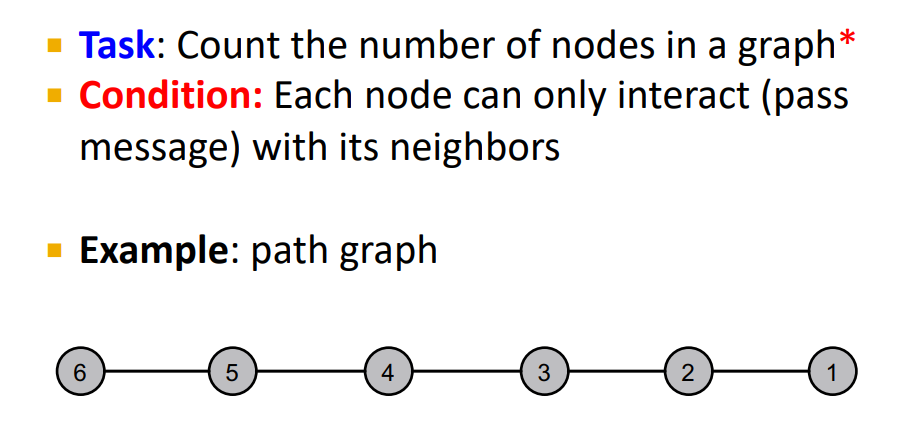
- Define an ordering of nodes

- Edge directions are according to order of nodes
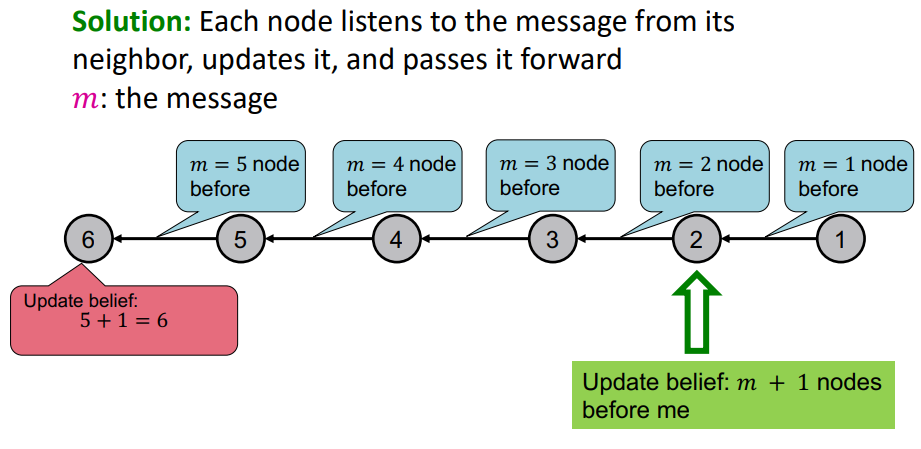
- Compute the message from node i to i+1 and Pass the message
-
이와 같은 방법은 Primitive 하지만 Powerful 하다.
-
또한 마지막 노드만이 Task에 대한 답을 알 수 있다.
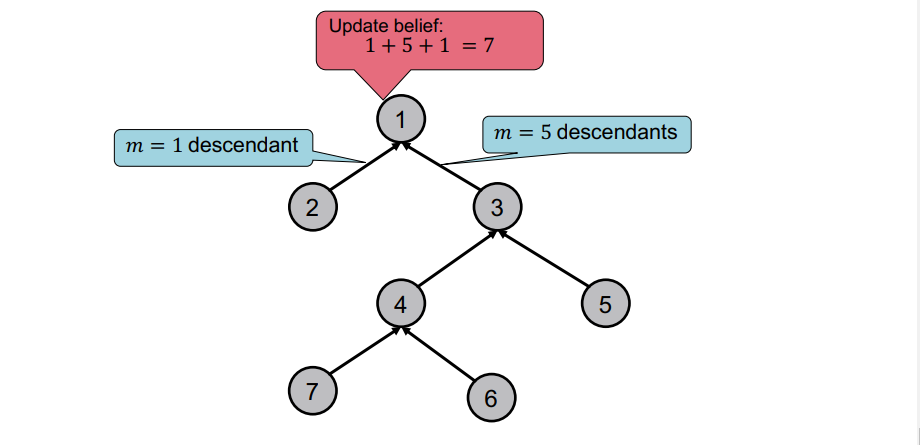
-
Tree 구조에도 이를 사용할 수 있다.
-
line graph나 tree의 root 만이 Task에 대한 정답을 알 수 있나 ?
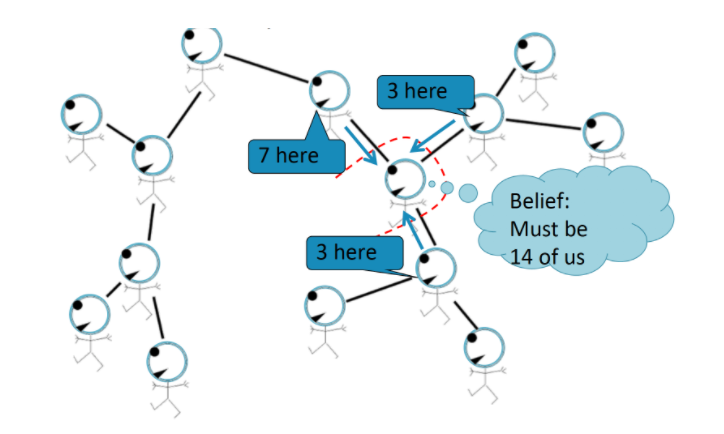
-
빨간색으로 표시된 노드 또한
Message Passing을 통해 Task에 대한 답을 할 수 있다 ! -
neighbors의 Belief를 통해 우리가 원하는 node의 Belief를 구할 수 있다 !
Loopy BP Algorithm
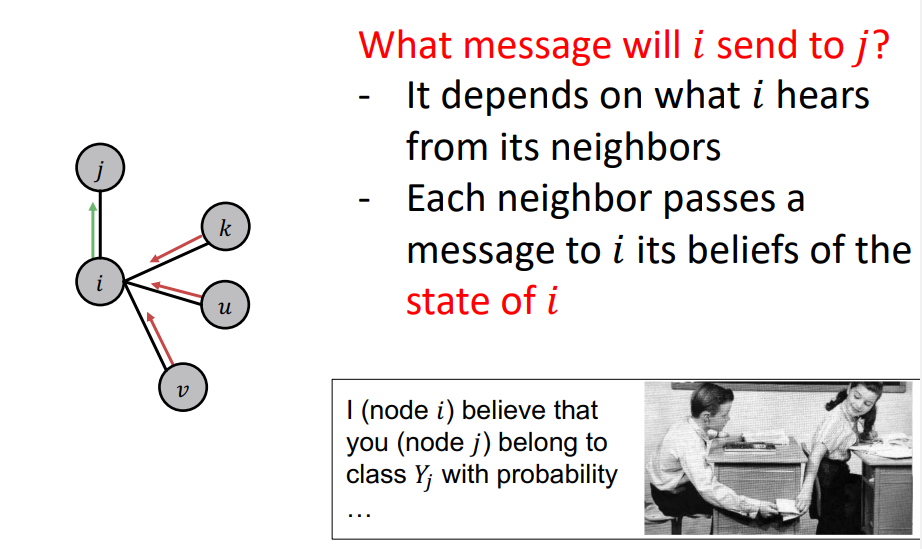
- Task : What message will i send to j ?
- node 가 주변 neighbors node 들로 부터 얻는 belief에 의존한다.
- 각각의 neighbor nodes 는 node 의 state에 대한 belief를 에게 message passing을 하고, 이러한 message를 통해 node 가 node 에게 passing 함.
Notation
-
: Label-label potential matrix
- labels에 대해서 node와 neighbors 사이의 dependency
- : 노드 j의 neighbor i가 state 에 있을 때, 노드 j가 state 에 속할 확률과 비례한다. = correlation between node
cf. Homophily에 대해서 Label-Label potential matrix가 high value on diagonal일 것이다. (node i 와 j의 class 가 같다) 만약 Big value off the diagonal 이면 node i와 j의 class는 다를 것이다.
-
: Prior Belief
- : node i 가 state 에 속할 확률
- node features capturing
-
: j가 state 에 대한 의 추정치
-
: 모든 states에 대한 집합 (class or labels)
Process
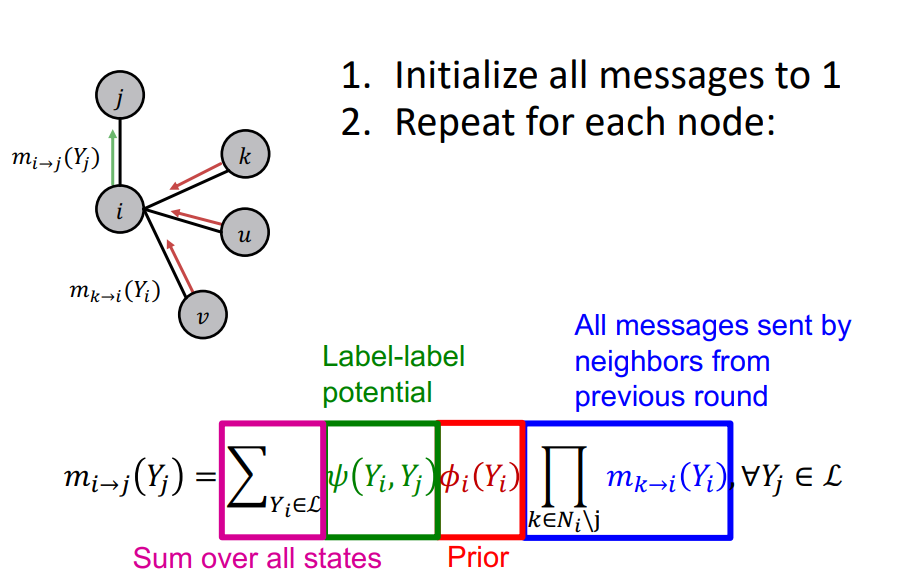
1. 모든 message들을 1로 초기화
2. 다음과 같은 방법을 반복 :
- node 의 neighbors로 부터 state 에 대한 belief를 message passing
- node 의 node features를 통해 state 에 속할 확률을 구한다.
- label-label potential matrix를 통해 를 구한다. ( 이 때 label-label potential matrix을 통해 구해진 값을 의 label이 의 label에 얼마나 영향을 끼치는지로 해석)
- 위에서 구한 값들을 통해 를 구한다.
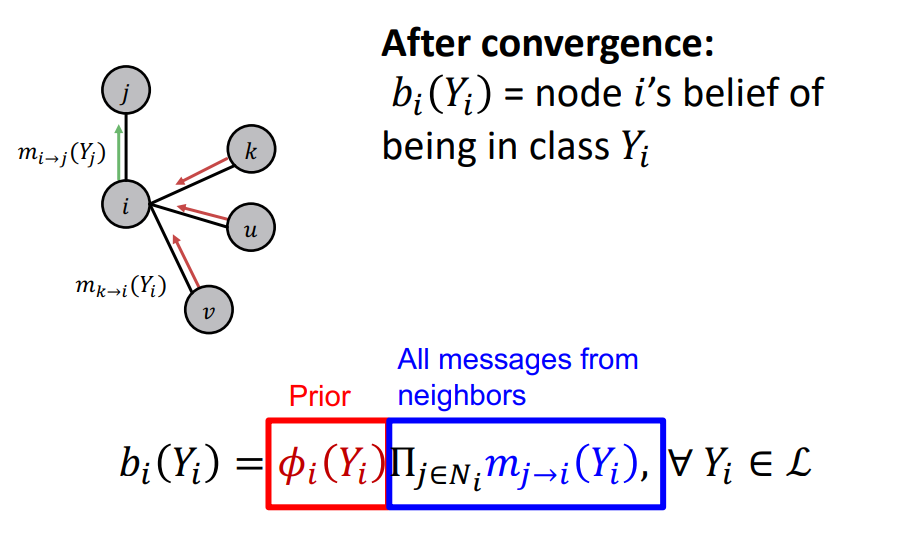
- 수렴하거나 max iteration이 되면, 각 state에 대한 Belief를 계산 !
Challenges
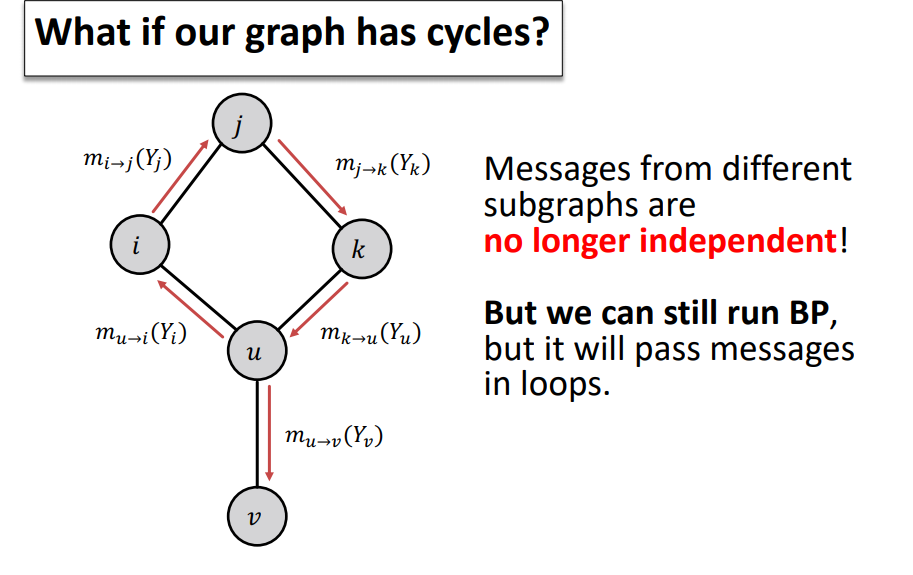
-
Loopy Belief Propagation은 Cycle이 있을 경우 잘 작동하지 않음 !
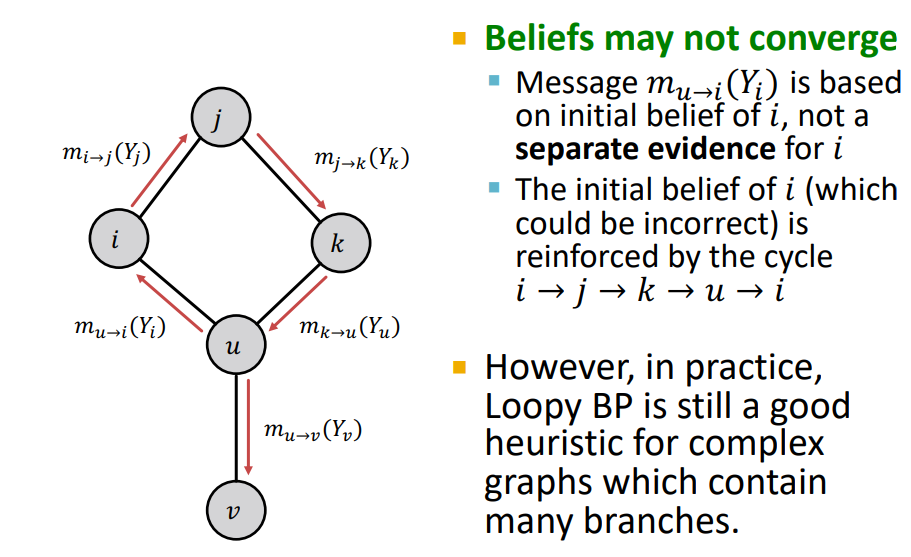
-
를 생각해보면, 이러한 cycle이 있으면 자기 자신의 정보를 반영하기 때문에 수렴이 되지 않음 !
-
걱정할 필요 없다 ! Real World의 Graph는 cycle이 작거나 발생하지 않는다 !
-
이러한 문제를 해결하기 위한 Heuristic한 방법도 많이 있다.
Summary
-
Advantages
-
프로그래밍 및 병렬화가 쉬움
-
label-label potential matrix를 통해 어떤 그래프 모델보다 general하게 적용 가능하다 (homophily 뿐만 아니라 node labels의 complex patterns도 학습 가능)
-
-
Challenges
-
수렴이 보장되지 않는다.
-
closed loop가 많으면 적용이 어렵다
-
-
Potential Functions
- parameter학습이 필요하다 (potential matrix, prior)
Reference
4개의 댓글
[14기 김상현]
- Collective classification은 동일한 label을 가지는 nodes는 연결되어 있다고 생각
Homophily: 개인의 특성 -> 사회적 연결
Influence: 사회적 연결 -> 개인의 특성 - Relational classifiers: 노드 v가 특정 label의 속할 확률을 주변 노드들의 가중합을 이용해서 구한다.
Semi-supervised learning: unlabeled node들의 확률을 균일하게 초기화 -> 주변 노드들의 확률을 가중합으로 노드 최신화 -> 반복 -> 수렴
수렴이 보장되지 않고, 노드의 feature information을 사용하지 않는다. - Iterative classification: feature vector만을 이용해 분류하는 분류기1과 feature vector와 network infromation을 이용해 분류하는 분류기2를 사용해서 예측
분류기1, 분류기2를 학습 -> 학습된 분류기들을 이용해서 예측 -> 반복 -> 수렴 - Belief propagation: 노드 간의 message passing을 통해 원하는 node의 belief를 구하는 방법
이전 노드에 전해진 메세지들의 곱에 prior와 label-label potential matrix를 곱해 이전 노드에서 현재 노드로의 메세지를 구함 -> 반복 -> 수렴
현재 노드에 전해진 메세지들의 곱과 prior의 곱으로 현재 노드의 belief를 구한다.
장점: 병렬화 쉬움, 일반적인 적용 가능성
단점: 수렴이 보장되지 않음, closed loop가 많은 경우 적용 어려움
Collective classification을 이용한 node classification 방법들을 이해할 수 있었습니다.
유익한 강의 감사합니다:)
[15기 김재희 - 강의 요약]
label 없는 노드에 대해 레이블을 예측하는 태스크를 수행하는 다양한 모델을 살펴보았습니다.
이때 semi-supervised 모델이 주로 활용됩니다.
0. Correlations Exist in Networks
네트워크 상에 존재하는 상관관계는 다음과 같이 두가지로 구분할 수 있습니다.
- Homophily : 비슷한 특성을 가진 노드가 서로 연결된다.
- Influence : 연결된 노드끼리 비슷한 특성을 가지게 된다.
1. Collective Classification
마르코프 체인을 이용하여 바로 이웃 노드의 레이블이 현재 노드의 레이블에 영향을 미치고 있다고 가정합니다.
이때
1. Local Classifier를 통해 초기 label 할당
2. Relational classifier를 통해 이웃 노드의 레이블 정보를 학습한 모델
3. Collective Inference : 각 노드마다 반복적으로 relational classifer를 inference 합니다.
2. Relational Classifier
이진분류를 가정합니다.
레이블이 있는 노드는 해당 레이블을 이용하고, 없는 노드는 0.5로 레이블을 초기화 합니다.
반복적으로 이웃 노드의 레이블의 가중평균을 통해 현재 노드의 레이블을 업데이트 합니다.
3. Iterative Classification
노드들의 변수도 활용하고자 하는 모델입니다.
이 현재 노드의 변수를 활용해 노드의 레이블을 초기화합니다.
가 이웃노드의 레이블 정보와 현재 노드의 변수를 고려하여 반복적으로 각 노드의 레이블을 예측합니다.
4. Belief Propagation
이웃노드로부터 받은 정보에 자신의 정보를 실어 다시 이웃노드로 보내는 과정을 반복하는 알고리즘입니다.
현재 노드가 받은 정보들을 모두 곱하고, 자신의 사전 정보를 곱하여 현재의 belief를 생성합니다.
다른 방법론에 비해 수렴이 보장되지 않습니다.
[15기 이성범]
이번 장에서는 Node Classification에 대하여 학습했다.
Collective Classification
- 네트워크 안에 상관성이 존재한다는 가정하에 이루어진다.
- Network에서 동일한 Label을 가지는 Nodes는 서로 연결되어 있다.
- Homophily(유유상종), Influence 라는 생각으로 인접한 노드를 가지고 unlabeled node들의 Class의 확률을 예측하는 것이 바로 Collective Classification 이다.
- Collective Classification의 관련 기술로는 Relational Classification, Iterative Classification, Belief Propagation 등이 존재한다.
- 위 기술이 가능한 이유는 마르코프 가정 덕분이다.
Relational Classification
Relational Classification는 node v에 class의 확률을 이웃 노드에 class의 확률의 가중 평균으로 구하는 방식이다.
먼저 unlabeled nodes의 확률을 0.5로 설정한 뒤에 max iteration 또는 모든 node가 수렴할 때 까지 unlabeled nodes의 확률을 업데이트 하면서 반복한다.
이러한 방식은 단순히 nodes의 label과 network information 만을 사용하기 때문에 수렴이 보장되지 않으며, 정확도가 높다고 볼 수 없다. 왜냐하면 node의 feature information을 사용하지 않기 때문이다.
Iterative Classification
Iterative Classification는 단순히 네트워크의 정보만 활용했던 Relational Classification에서 node의 feature information 까지 같이 활용하여 unlabeled nodes의 class 확률을 예측하는 방식이다.
먼저 training set을 통해 node의 feature를 활용해 node의 label을 예측하는 모델 1과 node의 feature와 이웃 노드의 라벨을 이용해 node의 label을 예측하는 모델 2를 학습시킨다.
그 후 먼저 모델 1을 통해서 node의 label을 할당하고 그 후 이웃 노드의 라벨을 활용해 모델 2를 통해서 최종으로 사용할 모델의 label을 예측한다. 이러한 방식 모델 1과 모델 2의 반복적인 학습을 수렴하거나 max iteration 까지 반복한다.
Belief Propagation
Belief Propagation은 Graphical Model에서 일부 노드에 대한 확률 분포 또는 값이 주어졌을 때, 다른 노드에 해당하는 확률 변수의 분포를 추정하는 방식이다.


[15기 황보진경 - 강의 요약]
Collective Classification. 동일한 라벨의 노드는 군집을 형성하고 있다고 판단한다.
Homophily(유유상종의 의미), Influence(커넥션이 개인에게 영향을 미친다)라는 특징을 가정하고 주변의 노드들을 이용하여 라벨이 없는 노드의 라벨을 예측한다.
Markov Assumption: 노드의 라벨은 노드의 1차 이웃들의 라벨에만 의존한다.
Collective Classification의 동작과정은 다음과 같다. 먼저 Local classifier에서 네트워크 정보는 사용하지 않고 노드의 attribute만을 이용하여 초기 라벨을 할당한다. 다음으로 Relational classifier에서 이웃들의 라벨 혹은 attribute를 사용하여 학습한다. Collective inference는 각 노드마다 Relational Classifier를 수행하여 원하는 노드의 라벨을 예측한다. 수렴이 쉽지 않기 때문에 일반적으로 정해진 iteration의 수만큼 반복하여 진행한다.