3주차 DeepAR 논문 리뷰

ToBigs1617 Time-Series·2022년 5월 6일

본 포스팅은 Jiyang Kang 님의 DeepAR 논문 리뷰 유튜브 영상을 바탕으로 작성하였습니다.

1. 서론

본 논문은 "어떻게 효과적으로 수요를 예측을 할 것인가?"라는 고민에서 출발한 논문으로, 아래 두 가지 문제점을 해결하고자 했다.

a) 수요 예측 문제는 대부분의 아이템은 거의 팔리지 않고, 많이 팔리는 아이템은 매우 적다는 특성을 가진다. 이에 따라 수요 데이터는 skew되어 있다는 특성을 지닌다.
b) 이전과 달리 수백, 수천만개의 방대한 다중 시계열 데이터를 기반으로 예측해야 함. 새로운 유형의 문제를 해결할 모델의 필요성 대두.

이에 따라 저자는 LSTM 기반의 확률론적 시계열 예측 모델인 “DeepAR”을 제시한다.

1-1. 수요 데이터의 고질적인 문제점

a)에서 언급한 데이터 특성은 아래의 그래프를 통해 쉽게 파악할 수 있다. 아래 그래프는 x,y축이 로그를 취한 값이기에 높은 수치의 판매량을 기록하는 제품의 수는 매우 적은 반면, 잘 팔리지 않는 제품의 수는 매우 큰 것을 보여준다.

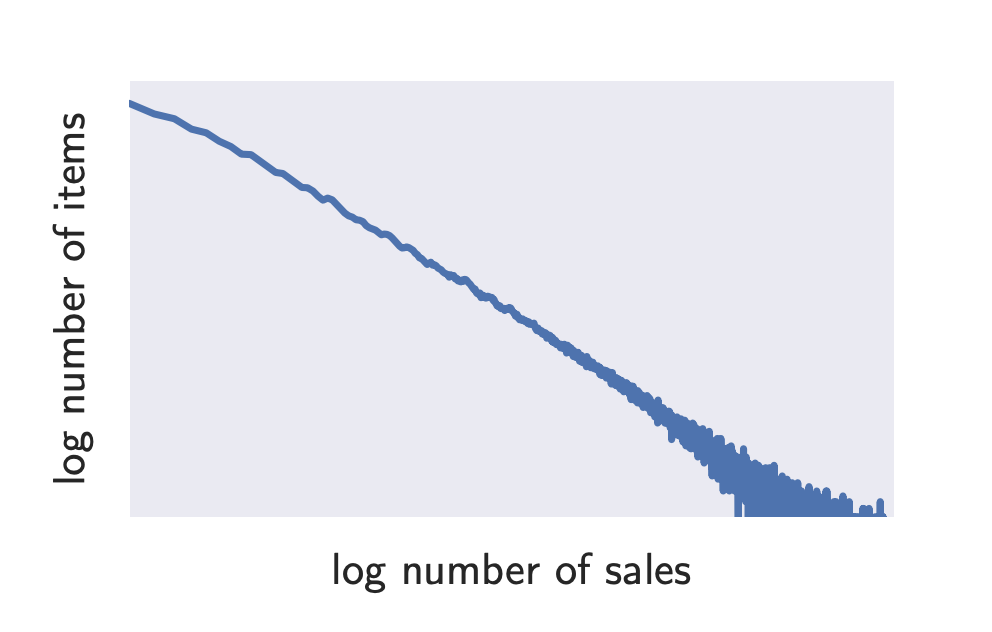
1-2. 분포와의 연관

이러한 데이터 특성은 시행횟수 n이 크고, 사건의 발생(성공) 확률 p는 매우 작은 경우에 사용되는 포아송분포와 연관지을 수 있다. X가 포아송분포를 따를 때, 포아송분포의 확률질량함수는

$Y \sim Pois(\lambda)$

$f_Y(y) = \frac{{e^{ - \lambda } \lambda ^y }}{{y!}}$

이는 뒤에 나올 음이항분포를 이해하는 기반이 된다.

1-3. 기존의 연구들

b)의 경우, 기존의 시계열 예측 연구들은 ‘Box-Jenkins methodology’(대표적으로 ARIMA) , ‘exponential smoothing techniques(지수평활법)’ 또는 ‘state space models’에 기반한다. 그러나 이러한 방법론들은 개별 시계열을 예측하는 모델로, 수백, 수천만 개로 훨씬 방대하고 복잡해진 다중 시계열 데이터를 예측하는 데에는 한계가 있다.
특히 수요 예측 영역에서 가우시안 오류, 등분산성 가정과 정상성 가정 위배와 같이 기본적인 가정들이 위배되는 경우가 많아 보다 일반적으로 사용될 수 있는 “likelihood function”(zero-inflated Poisson distribution,the negative binomial distribution)을 활용해 왔다.
복잡해진 시계열 데이터를 예측하기 위한 연구의 일환으로 베이지안 접근법이나 행렬분해 기법이 제안되었고 일부 신경망 모델을 사용한 방법론들이 있었지만 연산량이 상당히 복잡하거나 원하는 결과를 얻지 못했다.
이에 반해 RNN에 기반한 LSTM구조는 비단 예측 분야분 아니라 이미지, 자연어 처리, 음성변환 등의 분야에서 성공적으로 사용되어 왔다.

본 논문에서 제안하는 DeepAR은 두가지 측면에서 기존의 연구와 차이를 보인다.

probabilistic forecasting
출력값은 $t_0+1$ 시점의 단일 예측값이 아닌 해당 시점의 확률 분포를 모델링하는 파라미터가 output으로 출력된다. 이를 통해 불확실성을 고려한 최적의 의사결정 시스템을 구축할 수 있다는 장점이 있다. (downstream decision making)

Negative binomial likelihood
상한이 없는 수요량 데이터(count data)를 정확하게 예측하기 위해 음이항분포를 활용한다. 이는 직접적인 표준화작업은 어렵지만 정확도를 높여준다는 장점이 있다.

2. 모델

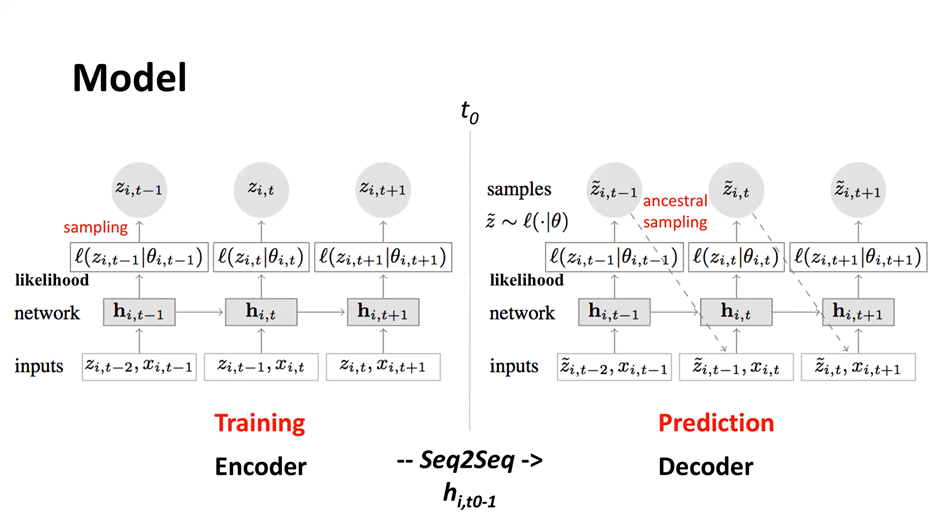
DeepAR모델은 그림과 같이 크게 encoder와 decoder로 나뉜다.
encoder의 경우,

t-2시점의 시계열 관측치 $z_{i,t-2}$ 와 다른 변수(covariates) $x_{i,t-1}$ 이 입력값으로 들어간다.
network단계에서는 가능도함수를 최대화하도록 오차역전파 방식으로 모수( $\theta$ )를 계산한다.
cf) 여기서 목적함수는 MLE이며, gaussian likelihood의 경우, 모수는 $\mu$ 와 $\sigma$ 에 해당한다. 해당 과정은 뒤에서 수식과 함께 알아보도록 하자.
이렇게 계산된 모수는 분포를 형성하게 되어 likelihood 함수를 도출한다.
해당 분포에서 샘플링을 통해 $z_{i,t-1}$ 을 출력한다.

decoder의 경우도 동일하다.
다만, 훈련 단계에서 decoder는 그림과 달리, 교사강요(teaching force) 방식으로 훈련한다. 이는 실제값을 통해 보다 정확한 훈련을 하게 하기 위함이다. 그림과 같이 이전 시점의 예측값이 다음 시점의 입력값으로 들어가는 경우는 실제 prediction에서 사용된다.

교사강요 방식
: t 시점의 입력값으로 t-1 시점의 예측 출력값이 아닌 실제값을 사용하는 것을 의미한다.

2-1. Likelihood model

Gaussian likelihood의 경우, 데이터 셋 중 0~1 사이의 확률값으로 나오는 실제 데이터의 분포를 찾기 위해 설정한 가능도함수이다. $\mu$ 함수의 경우, 은닉층의 셀 값에 $\mu$ 에 해당하는 가중치를 곱하고 편향을 더하여 도출된다. $\sigma$ 함수는 $\sigma$ 에 해당하는 가중치를 곱하고 편향을 더한 후, softplus activation이라는 활성화함수를 거쳐 도출된다.

softplus activation 함수의 기본 형태
: $log(1+exp(x))$ , $x$ :=input value
Negative binomial likelihood는 양의 이산형 확률변수인 주문량 데이터를 보다 정확하게 예측하기 위해 사용된다. Gaussian likelihood와 비슷한 방법으로 은닉층 셀 값에 가중치를 곱하고 편향을 더한 값을 softplus 활성화함수에 넣어 $\mu$ 와 $\alpha$ 를 도출한다.

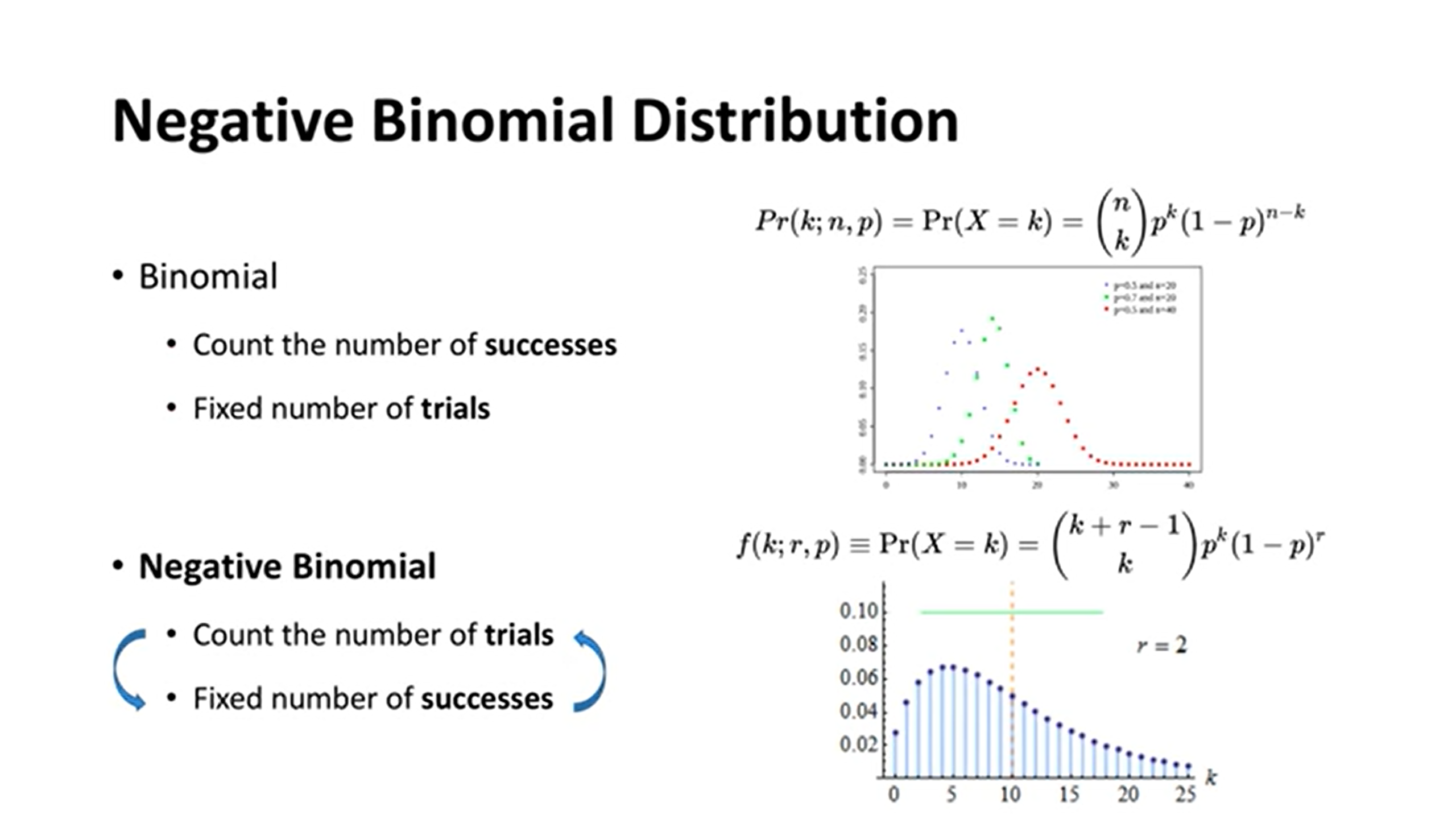
음이항분포(Negative Binomial distribution)에 대해 좀 더 알아보도록 하자.

Negative Binomial의 개념을 보다 쉽게 이해하기 위해 Binomial분포와 비교해보면,
이항분포의 경우, 총 시행 수는 고정되어 있고 성공의 횟수가 랜덤한 확률변수인 반면,
음이항분포는 성공의 횟수가 고정되어 있고 총 시행 수가 랜덤한 확률분포이다.
이항분포와 반대되는 확률변수 개념을 가졌다고 생각하면 쉽게 이해할 수 있다.

$\Gamma(x) = (x-1)!$

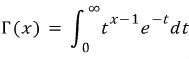
음이항분포의 확률변수는 두 가지 방법으로 정의할 수 있는데 <정의 2>와 같이 확률변수를 정의하고, $r=\frac{1}{\alpha}$ , $p=\frac{1}{1+\alpha\mu}$ 을 대입하면 논문에 나온 likelihood function과 동일함으로 확인할 수 있다.

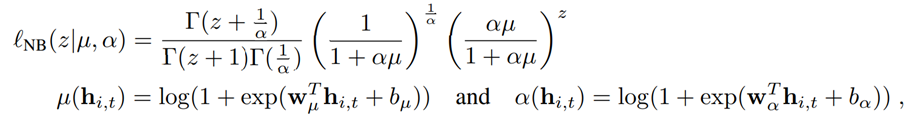
2-2. 복합포아송분포족으로서 음이항분포

논문에는 음이항분포를 수요 데이터셋에 적용하는 이유를 데이터의 magnitude가 방대하다는 점과 정확도 향상에 유의미하다는 결론을 제시하지만 해당 분포를 사용하는 수리적인 이유는 증명하지 않고 있다. 여기서 간략하게 설명하자면,

음이항분포는 복합포아송분포족(compound poisson distribution family)의 분포 중 하나이다. 여기서 복합 분포(compound distribution)란,
$Y=X_1+X_2+...+X_N$ 에서 $N$ 은 랜덤한 확률변수이고 $X_i$ 는 independent identically distributed(iid)이며 $N$ 와 $X_i$ 가 독립일 경우, $Y$ 는 복합분포를 따른다고 본다.

$N\sim Poisson(\Lambda)$ 이고,
$\Lambda\sim Gamma(\alpha,\beta)$ 일 경우, 해당 분포는 음이항분포로 볼 수 있다.

2-3. 음이항분포를 사용함으로써 얻는 이점

포아송분포를 likelihood로 사용할 경우, 단위 시간동안 주문이 몇번 발생하는지만 알 수 있다. 하지만 앞서 언급한 바와 같이, 수요 데이터가 방대하고 복잡해지면서 하나의 주문 안에서 여러 상품을 주문하는 경우가 많아졌다. 따라서 상품 수까지 랜덤한 확률변수로 두는 것이 복합포아송분포족의 하나인 음이항분포이다.

즉, 음이항분포를 사용하게 되면 단위 시간동안 $N$ 번의 주문이 들어오고, $N\sim Poisson(\Lambda)$ , 하나의 주문 안에 있는 상품 수 또한 랜덤인 시계열 데이터를 처리할 수 있게 된다. 특히, 이 상품수가 Logarithmic Distribution을 따를 때, 정확도가 더욱 높다.

3. 훈련 단계

3-1. Window

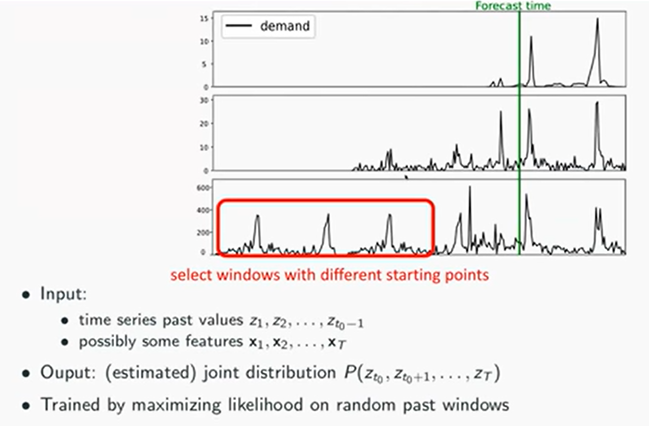
T길이의 window를 설정해서 학습시키는데 window의 시작점을 랜덤하게 둠으로써 다양한 시계열 window를 학습시킬 수 있도록한다. 여기서 window는 mini batch 개념과 연관지어 이해할 수 있다.

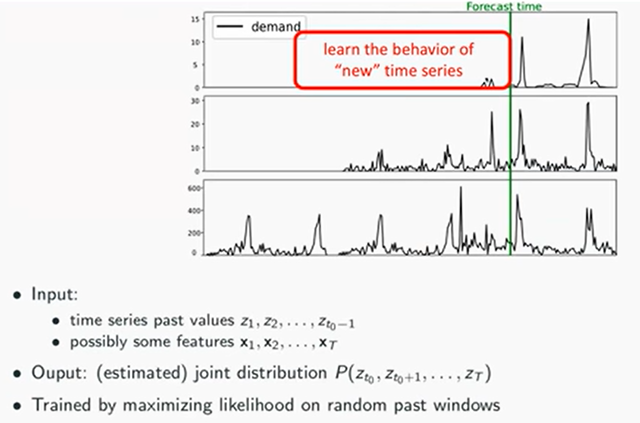
위 그림과 같이, 수요량이 없는 경우도 zero padding을 통해 window에 포함시킨다. 이유는 첫 주문, 첫 수요량 발생하는 시계열 형태를 학습하기 위함이다.

covariate( $x_{i,t}$ )과 함께 학습하기에 시계열 패턴뿐만 아니라 블랙프라이데이에 첫 수요가 발생했다면 다음 블랙프라이데이에도 수요가 발생할 것이라 예측하고, 해당 품목의 재고를 준비할 수 있음.

3-2. 목적함수

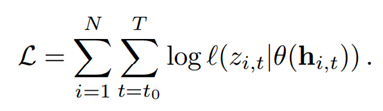
결합 확률 질량/밀도 함수에 로그를 취한 형태로, $L$ 을 최대화하는 모수(MLE)를 도출하도록 학습한다.

4. Scaling

4-1. 학습 시 두가지 문제점

데이터의 범위와 분산이 매우 크다
=> $v_i$ 로 입력값을 나눠주고, output(분포를 결정하는 모수)에 $v_i$ 를 곱해줌으로써 데이터가 왜곡되어 스케일링되지 않도록 한다.
$v_i = 1+\frac{1}{t_0}\Sigma_{t=1}^{t_0}z_{i,t}$
(휴리스틱으로 결정)
스케일이 매우 큰 데이터(수요량이 급증한 품목)은 매우 드물게 일어난다
=> 스케일이 큰 데이터는 더 자주 window에 포함되도록 가중치를 곱해, 확률을 조정한다. Window selection이 데이터별로 균등하지 않도록 weighted sampling을 해준다.

DeepAR 모델의 기타 장점

t시점의 결측치를 t-1시점의 관측치로 예측한 분포에서 샘플링함으로써 결측치를 쉽게 대체할 수 있다.
다양한 통계적 특성을 가진 데이터에 확장적으로 적용 가능하다.

unit interval을 가지는 데이터의 경우, Beta likelihood,
binary data의 경우, Bernoulli likelihood,
복잡한 주변확률분포 처리가 필요한 데이터셋은 mixture likelihood
미래의 불확실성을 잘 보여준다.

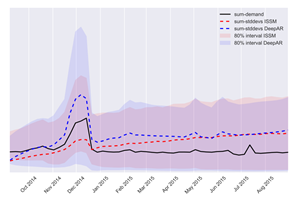
시간이 지날수록 불확실성을 나타내는 음영 부분이 wide해지는 것을 통해 확인할 수 있다.
신제품의 수요를 예측할 때 발생하는 cold-start 문제를 비슷한 제품의 수요 데이터를 활용하여 해결했다.

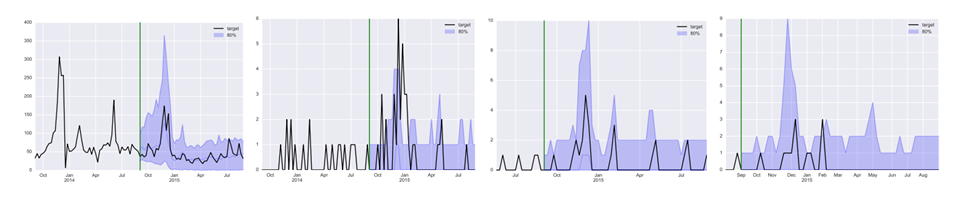
참고자료

Jiyang Kang 님의 DeepAR 논문 리뷰 유튜브 영상
복합포아송분포, 복합음이항분포 관련 블로그: https://mathmodelsblog.wordpress.com/2010/01/28/compound-negative-binomial-distribution/
seq2seq: https://bkshin.tistory.com/entry/NLP-13-%EC%8B%9C%ED%80%80%EC%8A%A4%ED%88%AC%EC%8B%9C%ED%80%80%EC%8A%A4seq2seq
MLE 설명 유튜브 강의: https://www.youtube.com/watch?v=XepXtl9YKwc&t=1s
고려대학교 송성주 교수님 수리통계학 강의안
고려대학교 김경희 교수님 확률론입문 강의안

작성자: 고려대학교 식품자원경제학과 김주호