Time Series is a Special Sequence : Forecasting with Sample Convolution and Interaction
Paper : https://arxiv.org/pdf/2106.09305.pdf
Github : https://github.com/cure-lab/SCINet

Abstract

Time series는 Sequence data의 일종이지만, Trend, Seasonality, 그리고 Irregular components로 분해될 수 있다는 독특한 특성을 지닙니다.
본 논문에서는 Time series의 특성에 기반해, Downsample-Convolve-Interact 구조로 구성된 SCINet(Sample Convolution and Interaction Network)을 제안합니다.
SCINet은 Time Series Forecasting(이하 'TSF')에서 현존하는 다른 방법론과 비교하여 우수한 예측 성능을 보입니다.

1. Introduction

전통적인 TSF 방법론(ARIMA, Holt-Winters 계절 방법론 등)은 단변량 예측 문제에는 적절하나, 실제 복잡한 다변량 데이터 예측에는 활용하기 어렵습니다.

이러한 전통적인 접근보다는 딥러닝 기반 기술들의 예측 성능이 더욱 뛰어난데, Sequence Modeling에 쓰이는 신경망은 아래처럼 크게 세 종류로 구분됩니다.

• RNNs(Recurrent Neural Networks) + LSTM(Long Short-Term Memory), GRUs(Gated Recurrent Units)
• Transformer
• TCN(Temporal Convolutional Networks)

위 방법론들은 예측을 잘 수행하기는 하지만, Generic Sequence Model에 기반하므로 다른 Sequence data와 구별되는 Time series만의 특성을 반영한 예측을 수행하지는 못합니다.

📌 Time series의 Unique Properties

• Downsampling을 수행하더라도 대부분의 정보 보존 가능
  - 일반적인 sequence data(text, DNA 등)와 차별화
• Trend, Seasonality, Irregular components로 구성

따라서, 본 논문에서는 TSF를 위해 특별히 고안된 SCINet을 제안합니다.

⭐ SCINet 핵심

• 계층적 TSF Framework
  : 각 temporal resolution에서 반복적으로 정보 추출 및 교환
• SCI-Block을 basic building block으로 활용
  : Input을 두 개의 sub-sequence로 downsampling + feature extraction

2. Related Work and Motivation

Related Work and Motivation 섹션에서는 딥러닝 기반 방법론을 활용해 다변량 time series에 대한 예측을 수행합니다.

2.1 Related Work

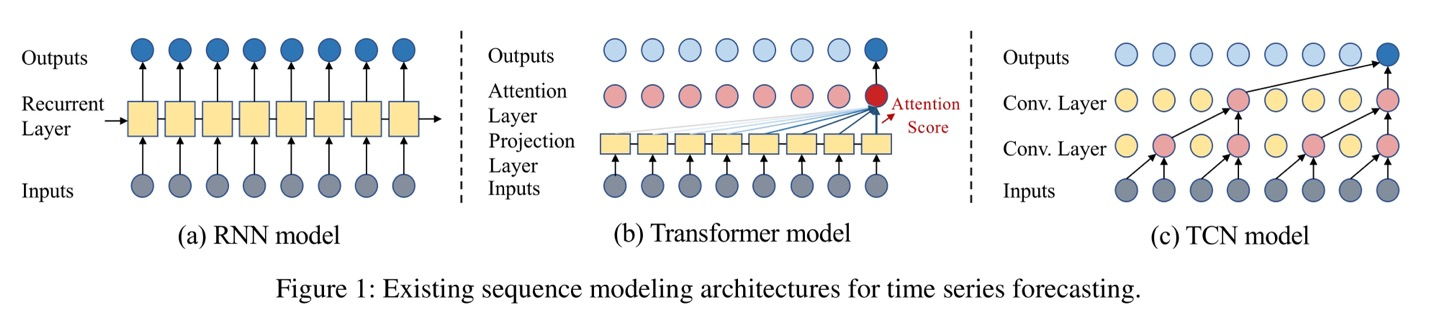
RNN-based Methods

• Figure 1의 (a)에서처럼 내부 메모리 state에 과거 정보가 압축되어 저장되고, 각 time step에서 새로운 input이 주어짐에 따라 메모리 state는 재귀적으로 update됩니다.
• Limitation : Memory constraint & Error accumulation, Gradient vanishing/exploding

Transformers

• Figure 1의 (b)에서처럼, Transformer는 Self-Attention 메커니즘을 이용해 Sequence Modeling task 대부분에서 RNN 모델들을 대체했습니다.
• Limitation : Overhead(간접비) of models, Lots of research efforts

Convolutional Models

• Convolutional filter들은 time series의 local correlation을 효과적으로 포착할 수 있으며, GNNs(Graph Neural Networks)와도 함께 잘 동작하여 spatial-temporal TSF 문제들을 해결하는 데 널리 쓰입니다.
• SCINet은 temporal convolution을 기본 구조로 하는데, dilated causal convolution에 기반한 기존 모델들과는 차이가 있습니다.

2.2 Rethinking Dilated Causal Convolution

• Notation
  • $X^*$ : time series
  • $T$ : length of a look-back window (fixed)
  • $t$ : timestamp

Causal Convolutions

• 예측을 수행할 때는 Causality가 반드시 보존되어야 하는데, 여기서 Causality란 특정 $t$ 시점의 output이 $t$ 시점 이전의 요소에만 의존하는 특성입니다.
• 즉, 미래 시점 정보가 역으로 흘러 현재 시점의 output에 영향을 미치는 문제가 있어서는 안 되고, 이러한 이유로 Causal Convolution은 IMS-based forecasting에만 적용되어야 합니다.

📌DMS estimation과 IMS estimation

• DMS(Direct Multi-Step) : Directly optimize the multi-step forecasting objective
• IMS(Iterated Multi-Step) : Learn a single-step forecaster and iteratively apply it to get multi-step predictions

Dilated Convolutions

• Dilated Convolutions를 활용하면 적은 수의 convolutional layer로도 receptive field를 넓힐 수 있습니다.
• 전형적인 TCN 구조에서는 Dilated Causal Convolutions를 활용하는데, 하나의 convolutional filter가 각 layer에서 공유되기 때문에 data나 feature의 temporal dynamics를 추출하기는 어렵다는 한계가 있습니다.

이에, SCINet에서는 Downsample-Convolve-Interact 구조로 Time series만의 특성을 고려해 예측 성능을 높였습니다.

3. SCINet : Sample Convolution and Interaction Networks

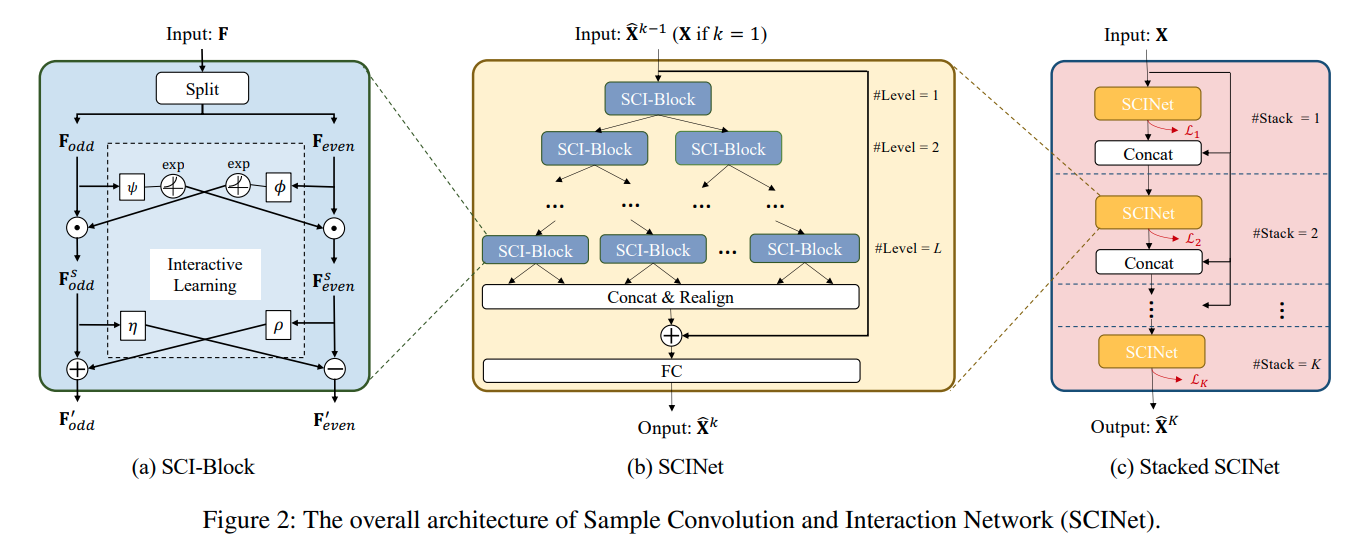
3.1 SCI-Block

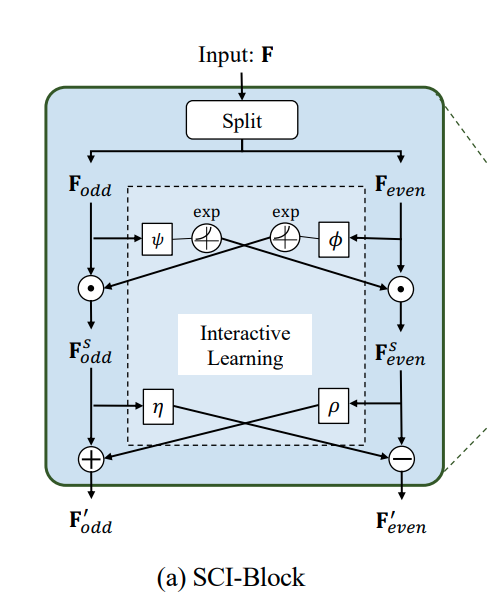
SCI-Block은 SCINet의 기본 module로, 'Splitting'과 'Interactive-learning'을 통해 Input feature $F$를 두 개의 sub-feature($F_{odd}$, $F_{even}$)로 분해합니다.

1. Splitting

• Original sequence $F$를 $F_{odd}$, $F_{even}$으로 downsampling (이때 $F$의 대부분의 정보는 보존됩니다.)
• $F_{odd}$, $F_{even}$에 대해 각기 다른 convolutional kernels를 사용합니다. kernel이 분리되어 있으므로, 각 kernel에서 추출된 feature들은 동질적인 특성과 이질적인 특성을 모두 갖추게 됩니다.
  

2. Interactive-learning

• Downsampling으로 인한 정보 손실에 대한 해결책으로 interactive-learning을 도입합니다. 이를 통해 두 sub-sequence 간 정보 교류가 상호 간 affine transformation parameter를 학습하는 방식으로 이루어집니다(information interchange).

위 과정을 수식으로 표현하면 아래와 같습니다.

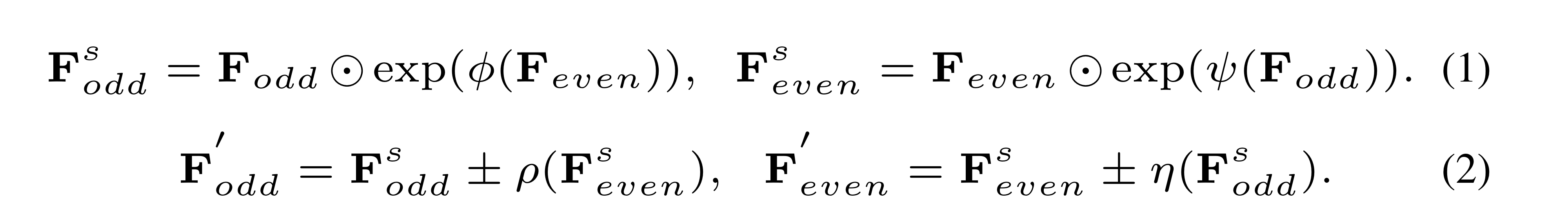
(1)

• $F_{even}$, $F_{odd}$은 각기 다른 kernel($\phi$, $\psi$)과 exponential 함수를 순차적으로 통과하고,
• 각각 $F_{odd}$, $F_{even}$와 element-wise product가 계산되어 $F^s_{odd}$, $F^s_{even}$으로 변환됩니다.

(2)

• $F^s_{even}$, $F^s_{odd}$은 각기 다른 kernel($\rho$, $\eta$)을 통과하고,
• +, - 연산자로 $F^s_{odd}$, $F^s_{even}$과 결합되어 최종적으로 $F^{'}_{odd}$, $F^{'}_{even}$으로 변환됩니다.

이를 통해 두 개의 downsampled sub-sequence로부터 핵심 정보를 추출해낼 수 있습니다.

3.2 SCINet

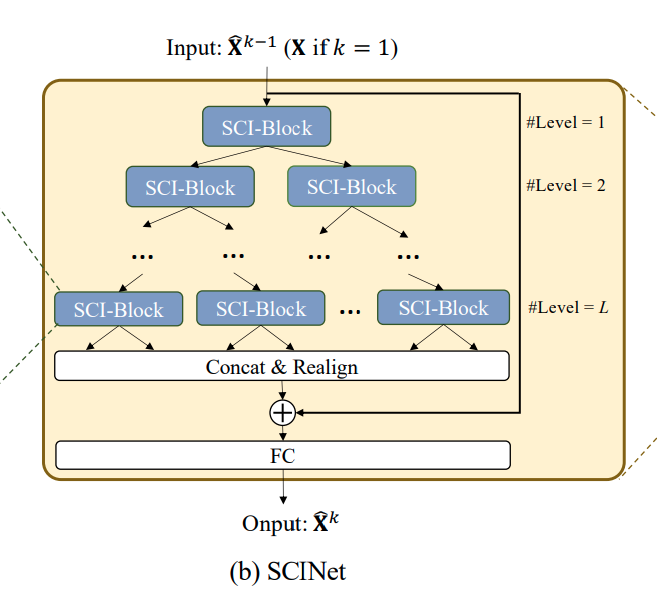
다수의 SCI-Blocks를 계층적으로 배치하여 tree-structured framework를 구성함으로써, SCINet이 구성됩니다.

SCINet의 구조를 살펴보면,

(1)

• $l$-$th$ level에는 $2^l$개의 SCI-Block이 있고, 총 level의 개수는 $L$입니다.
• 다음 level로 넘어가면서 Input time series(또는 feature vector)는 단계적으로 down-sampled되는데, 이로써 서로 다른 temporal resolution에서의 효율적인 feature learning이 가능해집니다.
• 또한 이전 level에서의 정보는 단계적으로 축적되고, 이러한 방식으로 TSF를 위한 short-term dependencies와 long-term dependencies 모두 보존할 수 있습니다.

(2)

• $L$ level의 SCI-Blocks를 통과하고 나서는, 모든 sub-features에 있는 요소들을 재배열합니다. (odd-even splitting operation에 대한 역변환 - 새로운 sequence representation으로 병합 - 이는 residual connection에 추가)
• 마지막으로 이러한 sequence representation을 decode하기 위해 fully-connected layer가 쓰입니다.

📌 How to choose $L$?

• 일반적인 경우에, SCINet에서는 original sequence 가장 coarse한 level까지 downsampling하지 않아도 됩니다.
• 본 논문에서는 $L$이 5 이하일 때 대부분의 case에서 best prediction results가 도출되었습니다.

3.3 Stacked SCINet

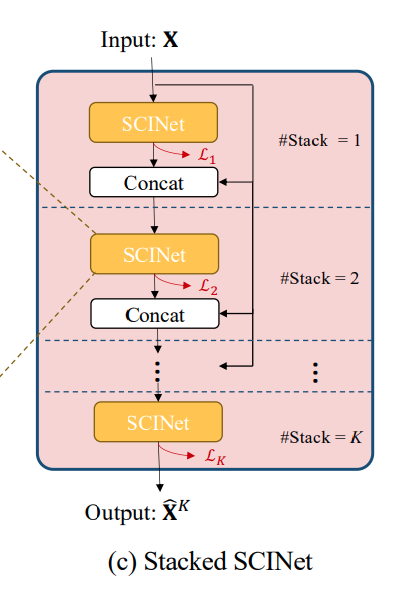
Training sample 수가 충분한 경우에는, SCINet layer를 여러 개($K$개) 쌓음으로써 훨씬 높은 예측 성능을 끌어낼 수 있습니다.
(참고로, 본 논문에서는 3개 이하로 쌓으면 충분함을 밝혔습니다.)

3.4 Loss Function

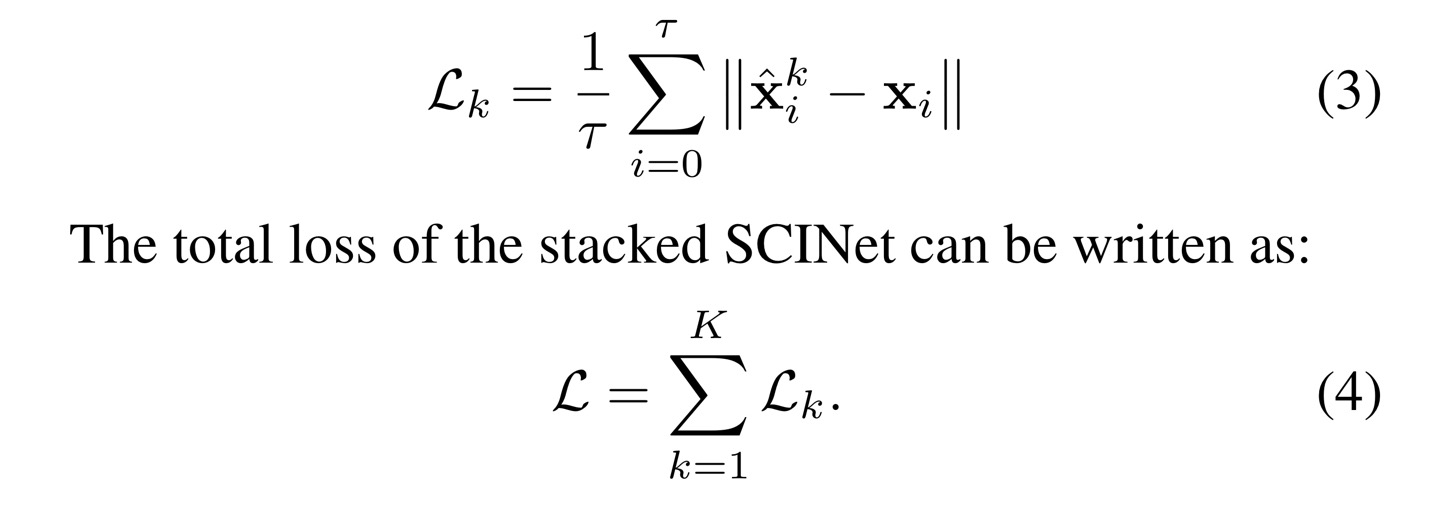
Stacked SCINet을 학습할 때, $k$번째 intermediate prediction의 loss로는 L1 loss가 사용됩니다.

4. Experiments

Experiments 섹션에서는 SCINet과 TSF에서의 SOTA 모델들 간 성능을 비교합니다.

4.1 Datasets

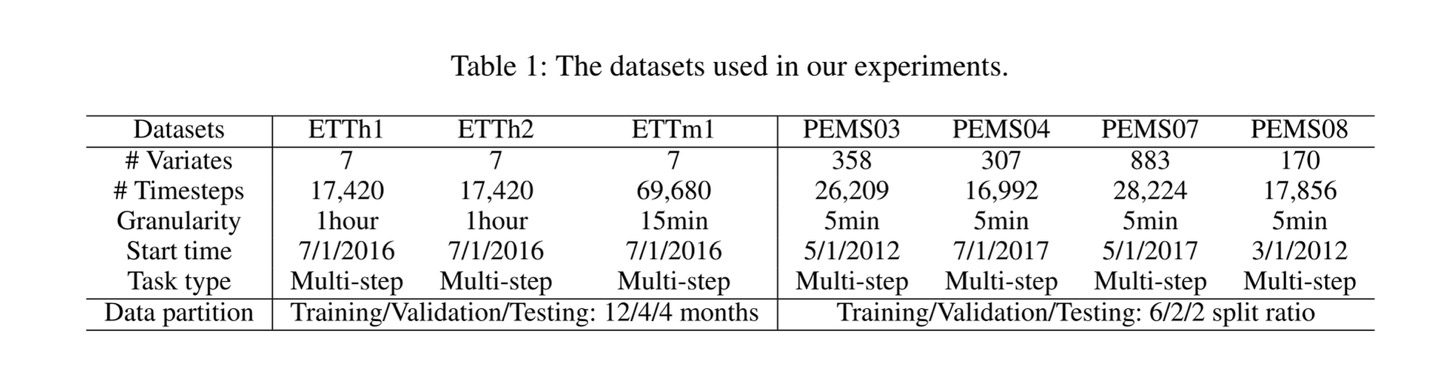
본 논문의 Experiments 섹션에서 사용한 Dataset은 Electricity Transformer Temperature(이하 'ETT')과 PeMS(traffic datasets)입니다.
정확한 성능 비교를 위해 metrics는 각 dataset의 original publication과 동일하게 사용했습니다. (ETT의 경우 MAE와 MSE, PeMS의 경우 MAE와 RMSE, MAPE)

위 Table 1에서 데이터셋에 대한 description을 확인하실 수 있습니다.

4.2 Results and Analyses

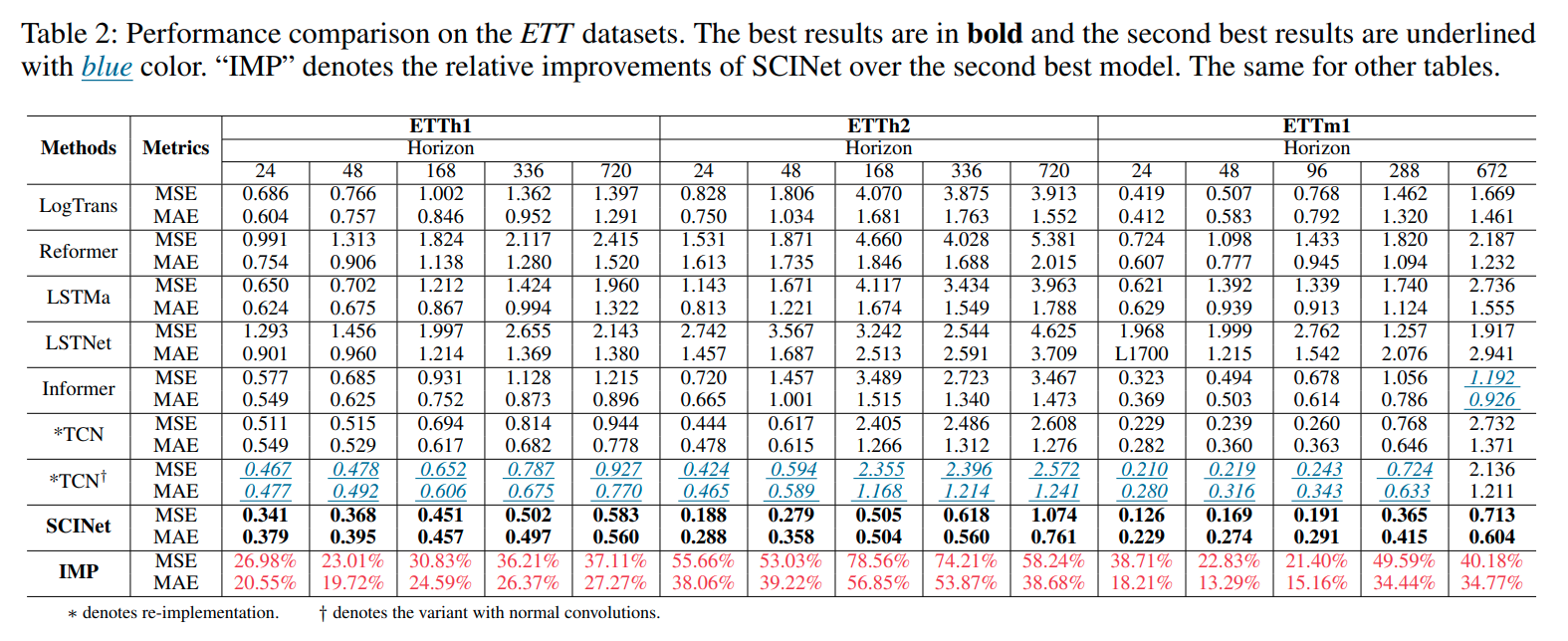
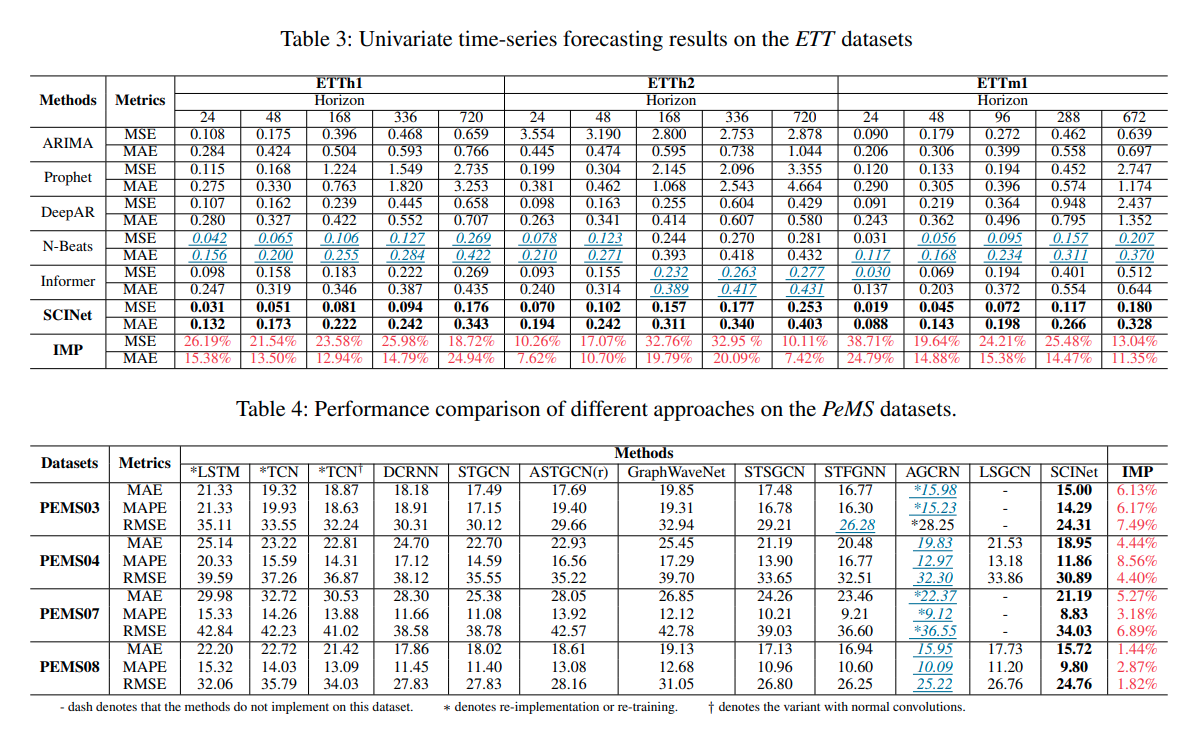
최근 제안된 다수의 SOTA 모델들과 비교해보았을 때, 유의미한 성능 개선이 입증되었습니다.

구체적으로는,

• SCINet이 다층의 temporal resolution으로부터 temporal dependencies를 잘 포착함이 입증되었습니다.
• (Table 3을 보면) 다른 baseline methods와 비교했을 때 압도적인 성능을 자랑하는 N-Beats(time series만의 unique properties를 고려하는 모델)보다도 SCINet은 성능이 좋았습니다.

5. Limitations and Future Work

• Noisy data에는 비교적 강건(robust)하지만, Missing data로 인한 성능 저하가 나타날 수 있습니다(missing data가 일정 비율(threshold) 이상일 경우).
• Irregular interval로 수집된 데이터셋을 잘 다루지 못합니다. (SCINet의 future development와 관련)

6. Conclusion

본 논문에서는 Generic sequence data와 구별되는 time series만의 독특한 특성에 기반한 새로운 neural network 구조인 'SCINet'이 소개되었습니다.

SCINet은 계층적인 구조로 설계되었으며, 반복적으로 각기 다른 temporal resolution에서 정보를 추출하고 교환함으로써 효율적인 feature representation을 수행합니다. Experiments 섹션에서 보인 바와 같이, TSF를 수행할 때 SCINet은 다른 SOTA 모델들과 비교했을 때도 압도적인 예측 성능을 보였습니다.

📖 Reference

• SCINet(2021)_논문 리뷰
• SCINet: Time Series is a Special Sequence: Forecasting with Sample Convolution and Interaction