DP로 최댓값 찾기

백준 2579번을 DP로 Java를 이용해 풀어봤다.
앞서 풀었던 9095번과 원리는 거의 동일하다고 볼 수 있다.

---

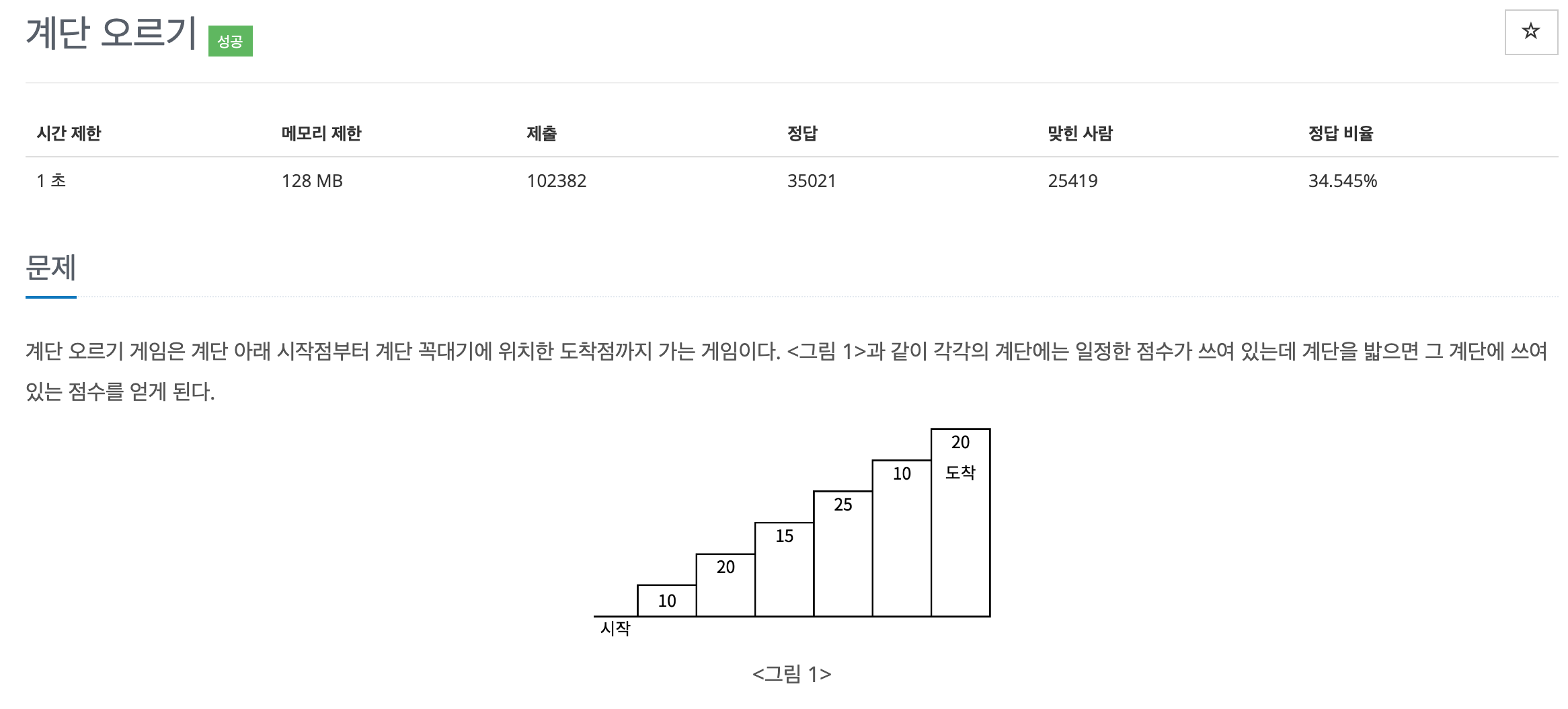
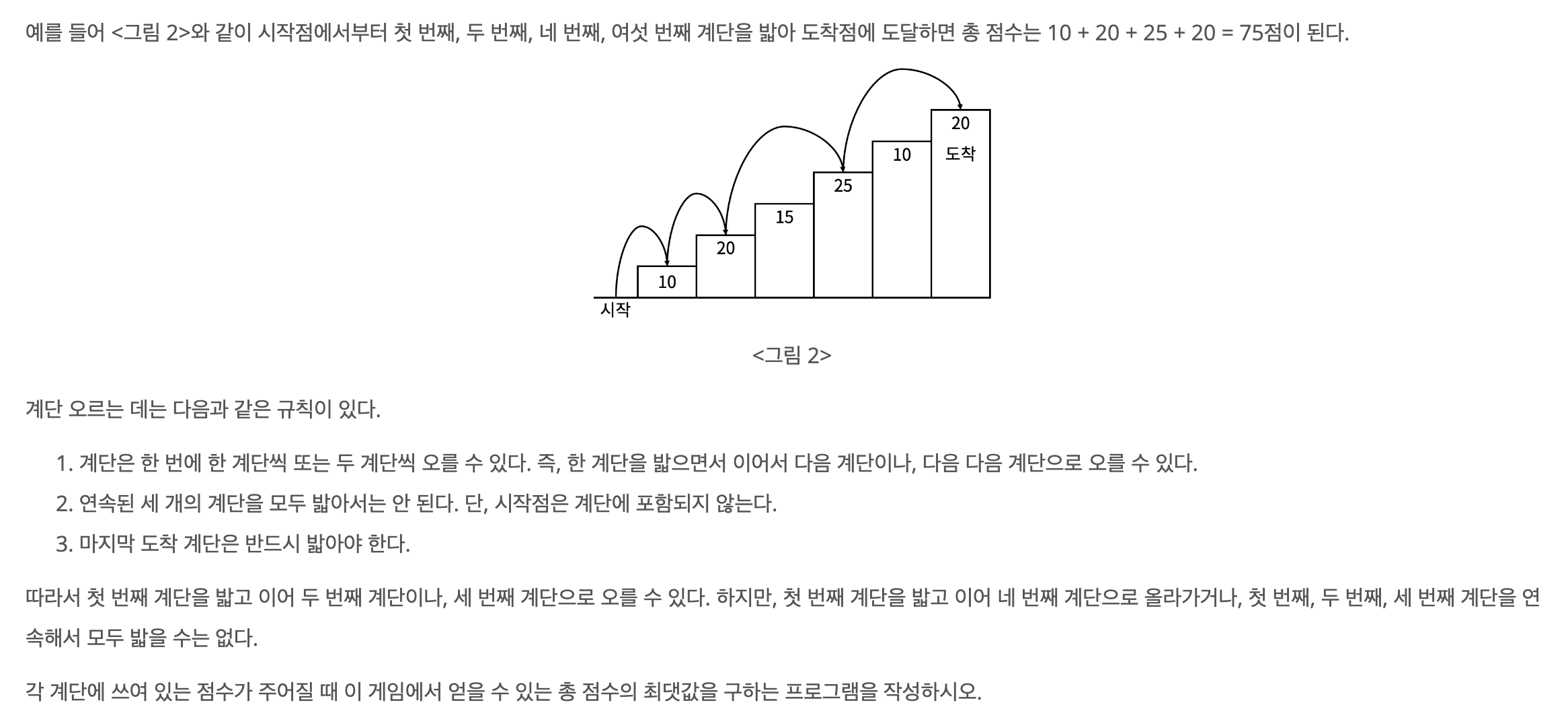
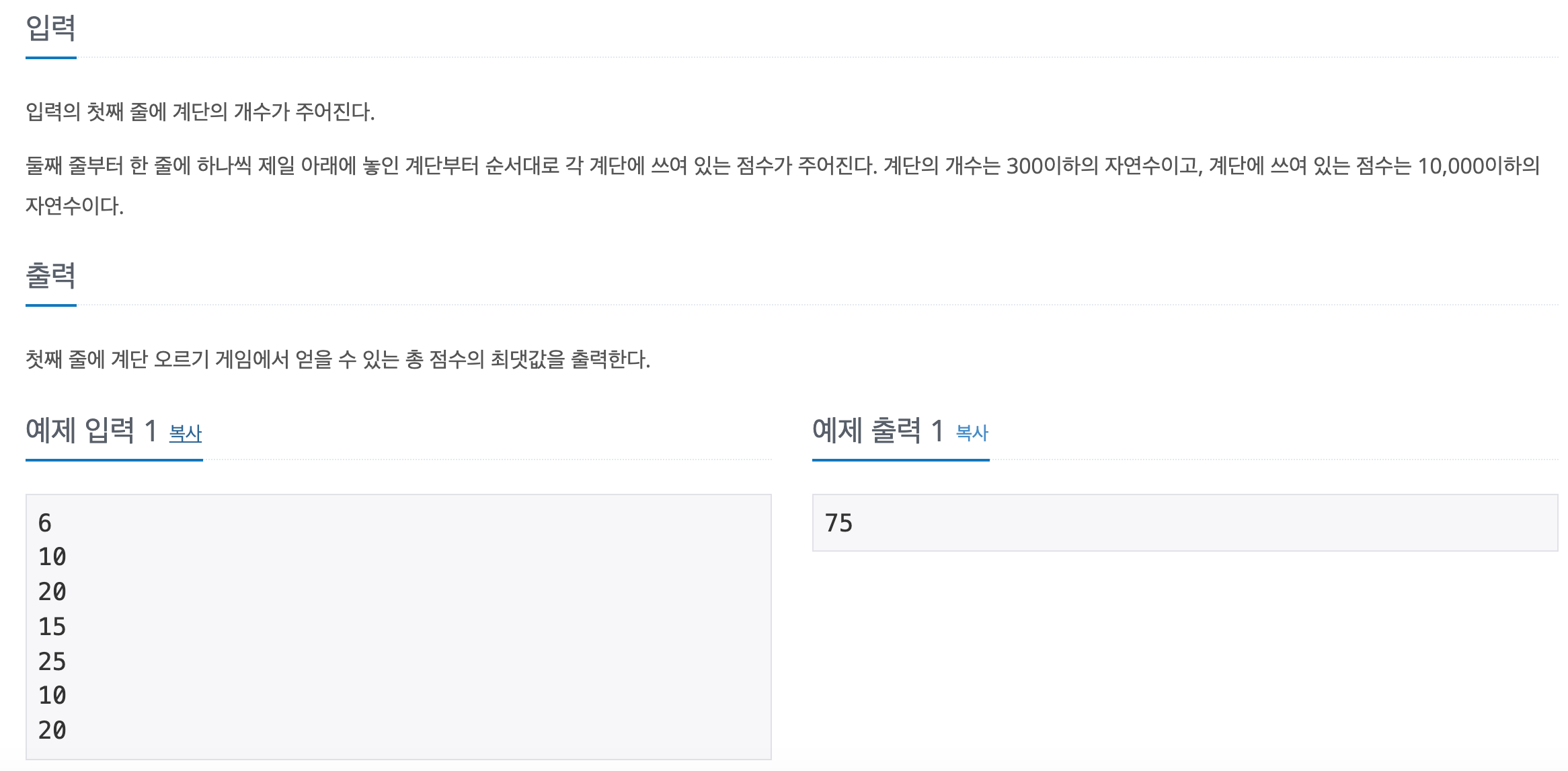
조건에 따라 움직이기

1칸 또는 2칸만을 움직일 수 있는 조건에 따라 점화식을 작성해주면 된다. 또한 최댓값을 구해야 하기 때문에 가능한 경로 중 어느 값이 더 큰지 판별해주는 정도만 하면 된다.

마지막에 1칸만 움직일 경우

직전 칸에서 1칸만 올라오려면, 이미 전 칸과 도착칸 2칸을 커버하고 있기 때문에 그 이전에는 반드시 도착점으로부터 3칸 전에서 출발했어야 한다. 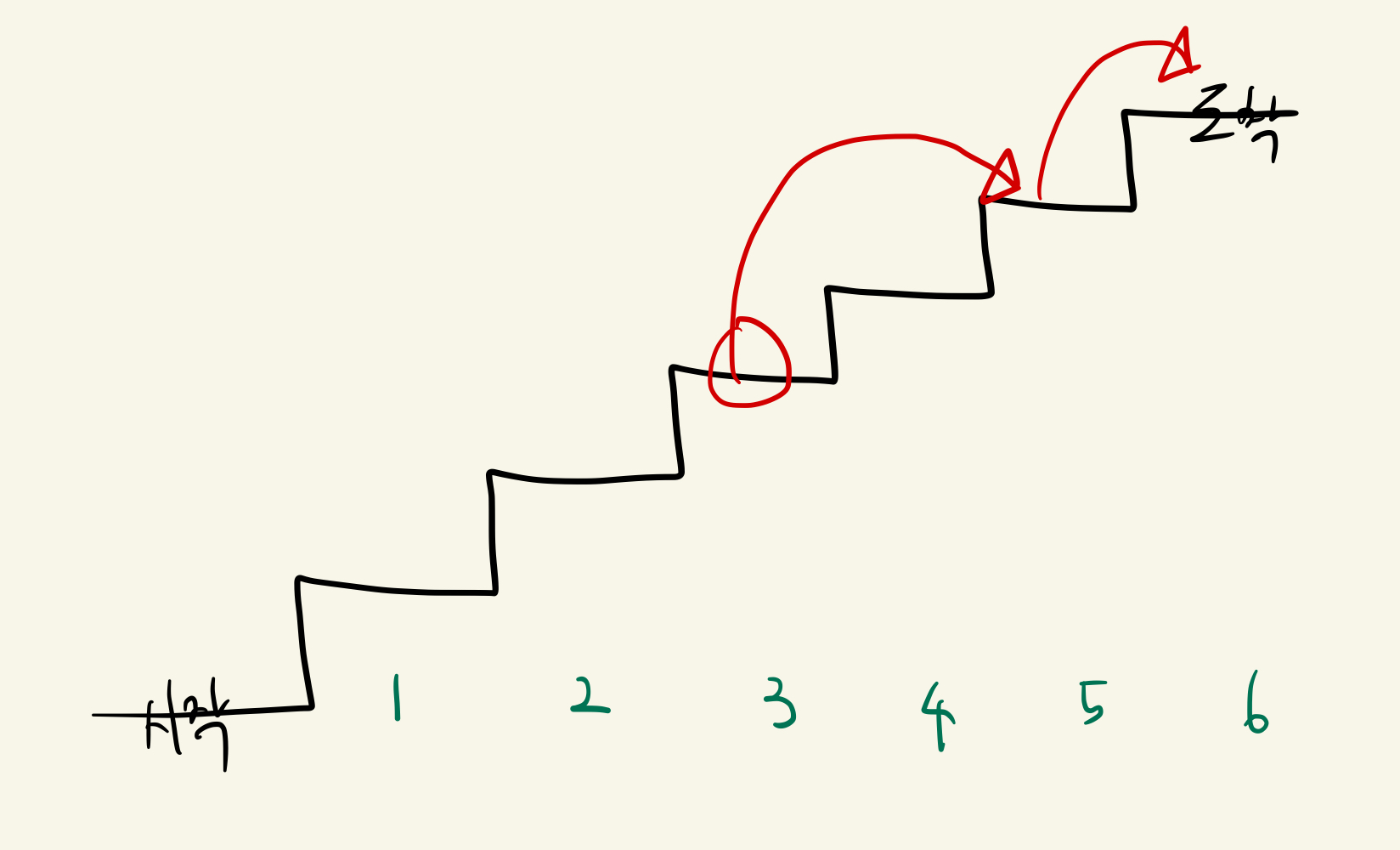말로 설명하니까 어지러운데,,, 그림으로 보는 것이 더 직관적이다.
6번 칸을 도착점으로 설정하자. 5번칸에서 한 칸 이동해서 도착했다면 5,6 이미 두 칸이 연속됨으로 그 전에는 반드시 3번칸에서 이동해왔어야 한다. 이를 식으로 표현하면 다음과 같다. (각 칸의 최댓값을 max[], 각 칸의 점수를 score[] 이라고 하자)

max[6] = max[3] + score[5] + score[6]

마지막에 2칸을 움직일 경우

마지막 move가 2칸을 움직인 경우는 2칸 전의 최댓값에 도착점의 점수만 더해주면 된다. 그림과 식으로 확인해보자.
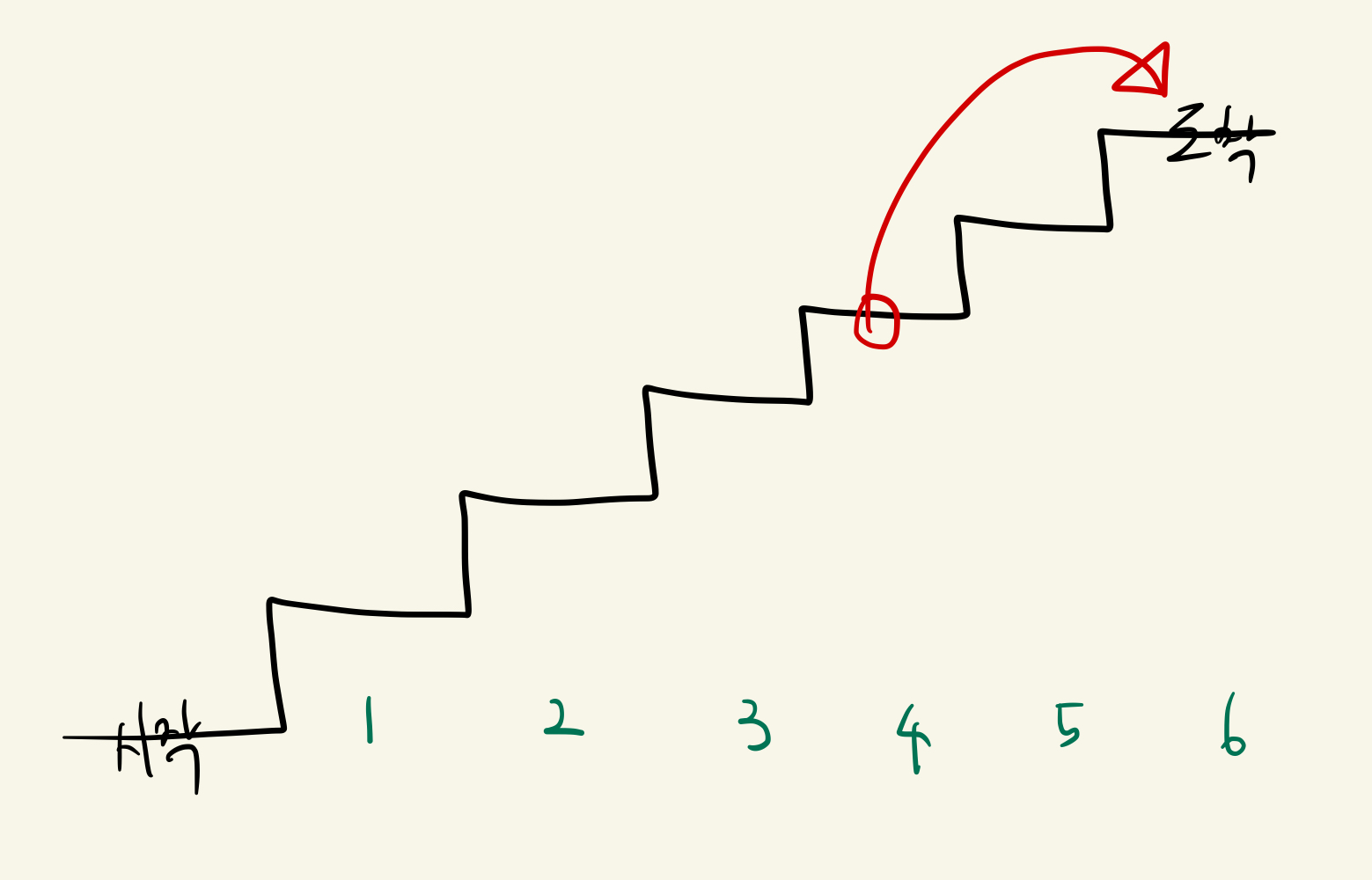4번칸에서의 최댓값에 6번칸의 점수를 더해주면 된다.

max[6] = max[4] + score[6]

최댓값 구하기

그럼 위의 두 가지 경우가 도출된 것에서 그 중 최댓값을 실제 max[n] 값으로 저장해주면 된다. 나는 먼저 1,2,3번 칸을 직접 초기화해준 후에 4번칸부터 for문을 이용해 Bottom-up 식으로 max배열을 초기화해주었다.

1. max[6] = max[3] + score[5] + score[6]
2. max[6] = max[4] + score[6]
   => max[6] = Math.max(1번, 2번)

---

아래는 내가 제출한 코드다.

import java.util.*;
import java.io.*;

public class boj2579 {
    static int n,score[] = new int[301], max[] = new int[301];

    static void DP(){
        max[1] = score[1];
        max[2] = score[1] + score[2];
        max[3] = Math.max(score[1]+score[3], score[2]+score[3]);

        for(int i=4; i<n+1; i++)
            max[i] = Math.max(max[i-2] + score[i], max[i-3] + score[i-1] + score[i]);
    }

    public static void main(String args[]) throws IOException {
        BufferedReader bfr = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer stk = new StringTokenizer(bfr.readLine());
        n = Integer.parseInt(stk.nextToken());

        for(int i=1; i<=n; i++){
            stk = new StringTokenizer(bfr.readLine());
            score[i] = Integer.parseInt(stk.nextToken());
        }
        DP();
        System.out.println(max[n]);
    }
}

처음에 score[]와 max[]를 n+1의 size로 초기화했더니 ArrayIndexOutOfBounds 나오길래 주어진 입력값의 범위인 300으로 초기화했더니 잘 된다.