DP로 경우의 수 찾기

백준 9095번을 DP를 이용해 Java로 풀어봤다.
간단한 DP문제였고 문제를 보자마자 바로 풀긴 했지만 솔직히 더 큰 수들을 넣어줬을 때도 반드시 맞는다는 보장이 있는가 에 대해서는 조금 망설여졌다.

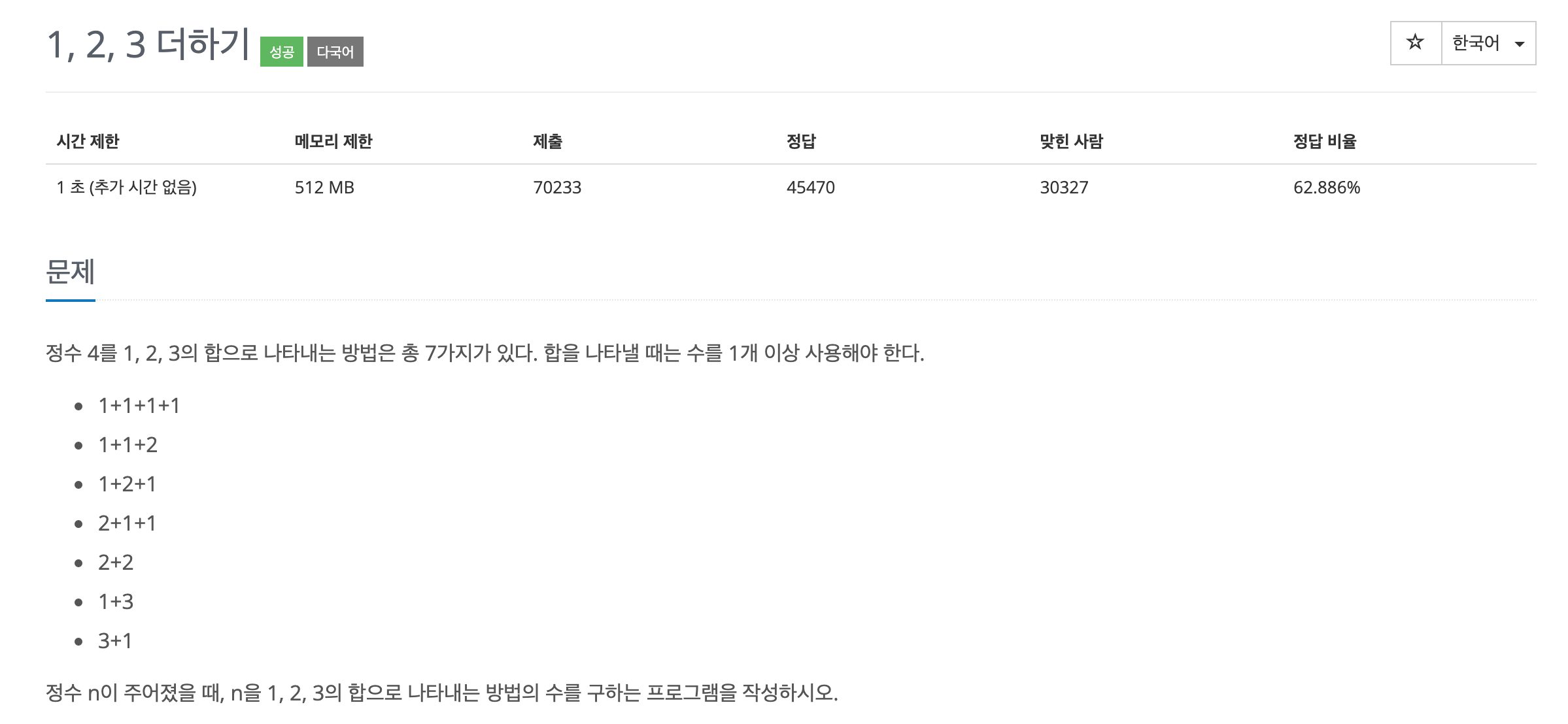
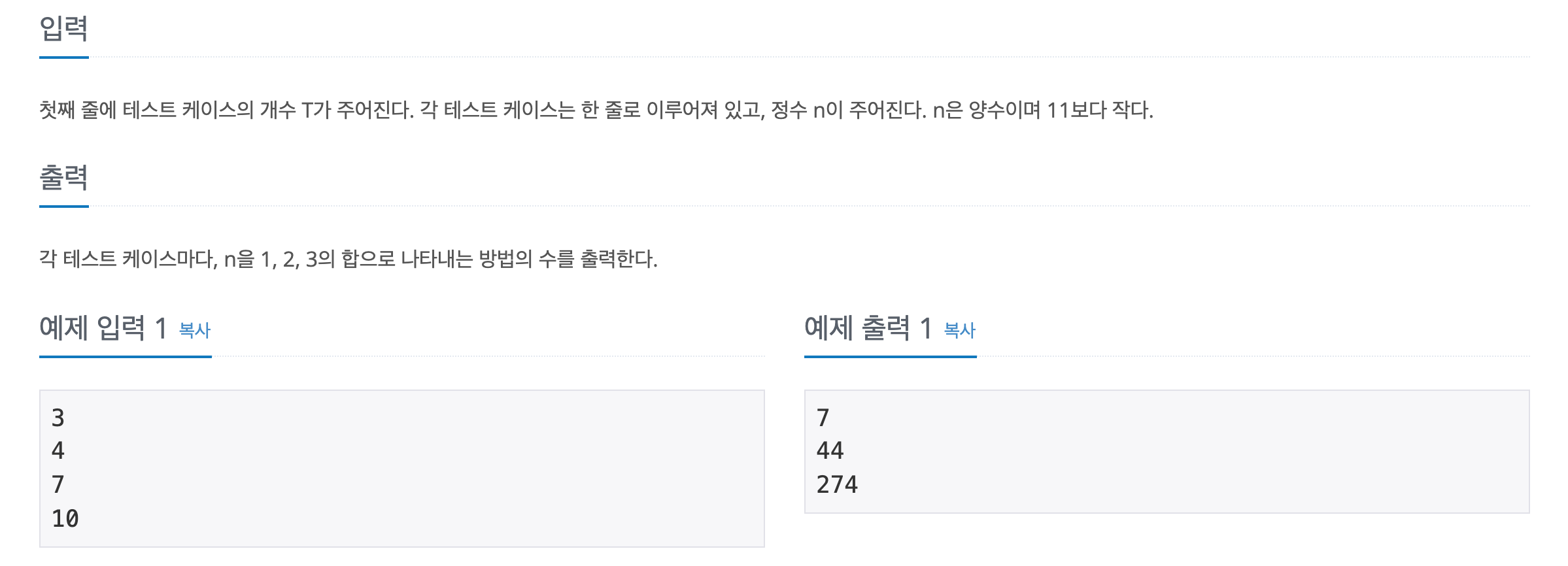
일단 제출하고 나서 다른 코드들도 살펴보며 생각해보니까 우리가 쓸 수 있는 수들은 1,2,3으로 고정되어 있다. 따라서 n을 만들고 싶을 때, 다음 세 가지 경우만 생각하면 된다.

1. n-3 + 3
2. n-2 + 2
3. n-1 + 1

이렇게 세 가지 경우만이 우리가 사용할 수 있는 표현 방법의 전부이기 때문에 다음과 같은 간단한 점화식이 도출되는 것이다.

dp[n] = dp[n-1] + dp[n-2] + dp[n-3]

아래는 내가 제출한 코드다.

import java.util.*;
import java.io.*;

public class boj9095 {
    static int T,n,dp[] = new int[11];

    static int DP(int n){
        if(dp[n]!=0)    return dp[n];
        else{
            for(int i=4; i<n+1; i++)
                dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
            return dp[n];
        }
    }

    public static void main(String args[]) throws IOException{
        BufferedReader bfr = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer stk = new StringTokenizer(bfr.readLine());
        T = Integer.parseInt(stk.nextToken());
        dp[1] = 1; dp[2] = 2; dp[3] = 4;
        for(int i=0; i<T; i++){
            stk = new StringTokenizer(bfr.readLine());
            n = Integer.parseInt(stk.nextToken());
            System.out.println(DP(n));
        }
    }
}