본 포스팅은 elice의 2021 NIPA AI 온라인 교육을 듣고 개인 공부를 위해 정리한 것입니다.

자료 형태의 이해

1. 자료의 형태

머신러닝은 데이터라는 디지털 자료를 바탕으로 수행하는 분석방식
자료의 형태를 파악하는 것은 머신러닝 사용하기 위한 필수 과정!

• 데이터가 어떻게 구성되어 있을까?
• 어떤 머신러닝 모델을 사용해야 할까?
• 데이터 전처리를 어떻게 해야 할까?

자료 형태 구분

수치형 자료

양적 자료라고도 한다.
수치로 측정이 가능한 자료
ex) 키, 몸무게, 시험 점수, 나이 등

범주형 자료

질적 자료라고도 한다.
수치로 측정이 불가능한 자료
ex) 성별, 지역, 혈액형 등

💎 자료 형태 구분 시, 주의점 💎

범주형 자료와 수치 자료의 구분 ≠ 자료의 숫자 표현 가능 여부

• 범주형 자료가 숫자로 표현되는 경우
  남녀 성별 구분 시, 남자를 1, 여자를 0으로 표현하는 경우
  👉 숫자로 표현되었으나 범주형 자료

• 수치형 자료를 범주형 자료로 변환하는 경우
  나이 구분 시, 나이 값은 수치형 자료지만 10 ~19세, 20 ~29세 등
  👉 나이 대에 따라 구간화하면 범주형 자료

범주형 자료

순위형 자료(Ordinal data)

범주 사이의 순서에 의미가 있음
ex) 학점(A+, A, A-)

명목형 자료(Norminal data)

범주 사이의 순서에 의미가 없음
ex) 혈액형(A, B, O, AB)

수치형 자료

연속형 자료(Continuous data)

연속적인 관측값을 가짐
ex) 원주율(3.1415926535....), 시간(09:12:23.21....) 등

이산형 자료(Discrete data)

셀 수 있는 관측값을 가짐
ex) 뉴스 글자 수, 주문 상품 개수

2. 범주형 자료의 요약

범주형 자료의 요약이 필요한 경우?

• 다수의 범주가 반복해서 관측될 때
• 관측값의 크기보다 포함되는 범주에 관심이 있을 때
  
  

범주형 자료를 요약하는 방식

1. 각 범주에 속하는 관측값의 개수를 측정
2. 전체에서 차지하는 각 범주의 비율 파악
3. 효율적으로 범주 간의 차이점을 비교 가능

도수분포표

범주형 자료에서 가장 많이 쓰인다.

아래의 표는 학생들을 상대로 한 강의 만족도 설문 조사(100명)이다.

No.	ID	만족도
1	23412	매우만족
2	12351	만족
3	12532	만족
4	25432	불만족
...	...	...
100	21353	보통

이 정보를 바탕으로 도수분포표를 그려보면 아래와 같다.

범주	도수	상대도수	누적 상대도수
매우만족	30	0.3	0.3
만족	10	0.1	0.4
보통	30	0.3	0.7
불만족	15	0.15	0.85
매우 불만족	15	0.15	1.00

• 도수는 범주에 해당되는 학생들이 얼마나 있었는지 나타낸다. 도수의 총 합은 100으로 학생의 인원이다.
• 상대도수는 도수를 전체 개수(100)로 나눠준 값이다. 쉽게 전체 대비 비율을 파악할 수 있다.
• 누적 상대도수는 특정 범주의 값을 한번에 구하고 싶을 때 사용한다.
  예를 들어 매우만족~보통의 비율은 0.7이다.

도수분포표 정의

• 도수(Frequency) : 각 범주에 속하는 관측값의 개수, value_counts()
• 상대도수(Relative Frequency) : 도수를 자료의 전체 개수로 나눈 비율, value_counts(normalize=True)
• 도수분포표(Frequency Table) : 범주형 자료에서 범주와 그 범주에 대응하는 도수, 상대도수를 나열해 표로 만든 것

막대그래프(Bar Chart)

각 범주들의 크기 차이를 잘 보여줄 수 있는 방법이 있을까? 👉 막대그래프!

위에서 봤던 예시를 다시 가져와봤다.

No.	ID	만족도
1	23412	매우만족
2	12351	만족
3	12532	만족
4	25432	불만족
...	...	...
100	21353	보통

이를 막대그래프로 나타내면 아래와 같다.

이렇게 막대그래프를 사용하면 각 범주가 얼마나 크기가 있고 얼마나 차이가 나는지 파악하기가 쉽다. 파이썬에서 막대그래프를 출력하려면 matplotlib 라이브러리의 plt.bar()를 사용하여 그릴 수 있다.

막대그래프의 특징

각 범주에서 도수의 크기를 막대로 그림

• 그래프의 x축 : 범주를 나열
• 그래프의 y축 : 도수에 대한 눈금

장점 : 각 범주가 가지는 도수의 크기 차이를 비교하기 쉬움
단점 : 각 범주가 차지하는 비율의 비교는 다소 어려움

실습✍ 범주형 자료의 요약 - 도수분포표

A, B, C, D, E 이 다섯 명의 술자리 참여 횟수가 기록된 데이터를 저장한 파일인 drink.csv 파일을 이용하여 누가 제일 술자리에 자주 나왔는지 value_counts() 함수로 계산한 도수로 확인해보자

• Attend : 참석한 경우 1, 참석하지 않은 경우 0
• Name : 참석자의 이름

• drink['Name'].value_counts() : Name열의 도수 출력
• drink.csv의 정보 : drink.head() (상위 5개), drink.info()결과

   Attend Name
0       1    A
1       0    A
2       1    A
3       1    A
4       1    A
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 25 entries, 0 to 24
Data columns (total 2 columns):
Attend    25 non-null int64
Name      25 non-null object
dtypes: int64(1), object(1)
memory usage: 480.0+ bytes

drink.csv에서 참석한 사람 중 이름에 따른 도수를 계산한 코드를 입력하여 drink_freq 에 저장해보자

• 답안 작성하기 : drink[drink['Attend']==1]["Name"].value_counts()

import pandas as pd 
import numpy as np

# drink 데이터
drink = pd.read_csv("drink.csv")


"""
1. 도수 계산
"""
drink_freq = drink[drink['Attend']==1]["Name"].value_counts()

print("도수분포표")
print(drink_freq)

• 결과

도수분포표
A    4
B    3
D    2
C    2
E    1
Name: Name, dtype: int64

실습✍ 범주형 자료의 요약 - 막대그래프

앞의 실습의 결과를 통해 막대그래프를 그려보자

참석 비율(ratio)을 기준으로 막대그래프 막대의 크기를 다르게 하는 코드를 작성하여 출력해보자

• 답안 작성하기 : plt.bar(labels, ratio)

from elice_utils import EliceUtils
import matplotlib.pyplot as plt
elice_utils = EliceUtils()    
# 술자리 참석 상대도수 데이터 
labels = ['A', 'B', 'C', 'D', 'E']
ratio = [4,3,2,2,1]
    
#막대 그래프
fig, ax = plt.subplots()

"""
1. 막대 그래프를 만드는 코드를 작성해 주세요
"""
plt.bar(labels, ratio)

# 출력에 필요한 코드
plt.show()
# 아래는 elice 플랫폼에서 그림 파일 출력 위한 코드
fig.savefig("bar_plot.png")
elice_utils.send_image("bar_plot.png")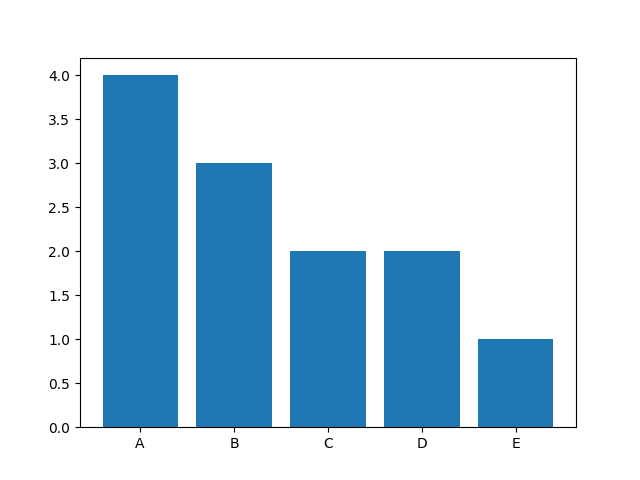

3. 수치형 자료의 요약

수치형 자료의 특징

• 범주형 자료와 달리 수치로 구성되어 있기에 통계값을 사용한 요약이 가능함
• 시각적 자료로는 이론적 근거 제시가 쉽지 않는 단점을 보완함

👉 많은 양의 자료를 의미 있는 수치로 요약하여 대략적인 분포상태를 파악 가능

평균(Mean)

np.mean()
관측값들을 대표할 수 있는 통계값
수치형 자료의 통계값 중 가장 많이 사용되는 방법
모든 관측값의 합을 자료의 개수로 나눈 것

자료 $x_1, x_2, ..., x_n$의 평균을 $\overline{x}$로 표기

$\overline{x}$ = ${모든\,관측값의\,합계}\over{총\,자료의\,개수}$ = ${x_1 + x_2 + \cdots + x_n}\over{n}$

평균의 특징

• 관측값의 산술평균으로 사용
• 통계에서 기초적인 통계 수치로 가장 많이 사용
• 극단적으로 큰 값이나 작은 값의 영향을 많이 받음
  👉 이상치가 있을 경우 값이 왜곡될 가능성이 있다.

퍼진 정도의 측도 : 분산, 표준편차

평균만으로 분포를 파악하기에 부족해서 평균 외에 분포가 퍼진 정도를 측도할 수치가 필요해졌다. 분산과 표준편차가 대표적인 퍼진 정도의 측도이다.

위 세 개의 자료는 평균이 모두 같으나 분산이 다르게 다온다. C가 분산이 가장 큰데 분산이 클 수록 더 퍼져있다.

분산

from statistics import variance
variance()

자료가 얼마나 흩어졌는지 숫자로 표현
각 관측값이 자료의 평균으로부터 떨어진 정도를 나타낸다.

표준편차

from statistics import stdev
stdev()

분산의 단위는 관측값의 단위의 제곱과 같다!
→ 관측값의 단위와 불일치!
→ 분산의 양의 제곱근은 관측값과 단위가 일치
이 분산의 양의 제곱근을 표준편차로 하고 s로 표기한다.

$s$ = $+\sqrt{s^2}$

분산이 커지면 표준편차도 커지도 분산이 작아지면 표준편차도 작아진다.

이제 통계값을 바탕으로 시각화를 해보자

히스토그램

plt.hist()
수치형 자료를 일정한 범위를 갖는 범주로 나누고 막대그래프의 같은 방식으로 그림

도수를 비교하여 범주형 자료이면 막대그래프, 수치형 자료이면 히스토그램을 그린다고 생각하면 된다!

히스토그램의 특징

• 자료의 분포를 알 수 있음
• 계급구간과 막대의 높이로 그림
• 도수, 상대도수를 막대 높이로 사용

실습✍ 수치형 자료의 요약 - 평균

• 카페별 카페인 함량

카페	카페인 함량	카페	카페인 함량
커빈피	202	빽방다	177
스벅타스	121	할스리	148
디야이	89	동네카페	121
투썸플이레스	137	엔제너리스	158

이 표를 참고로 커피 한 잔 당 평균적으로 얼마나 카페인이 들어있을지 산술평균을 계산해서 확인해보자!

• 답안 작성하기 : `mean = np.mean(array)

import numpy as np

coffee = np.array([202,177,121,148,89,121,137,158])

"""
1. 평균계산
"""
cf_mean = np.mean(coffee) # coffee.mean() 도 가능

# 소수점 둘째 자리까지 반올림하여 출력합니다. 
print("Mean :", round(cf_mean,2))

• 결과

Mean : 144.12

실습✍ 수치형 자료의 요약 - 표준편차

coffee에 저장된 카페인 함량 값들의 표준편차를 계산해서 cf_std 에 저장해서 확인해보자

• 답안 작성하기 : std = stdev(array)

from statistics import stdev
import numpy as np

coffee = np.array([202,177,121,148,89,121,137,158])

"""
1. 표준편차 계산
"""
cf_std = stdev(coffee)

# 소수점 둘째 자리까지 반올림하여 출력합니다. 
print("Sample std.Dev : ", round(cf_std,2))

• 결과

Sample std.Dev :  35.44

• 만약 분산을 구하고 싶다면?
  표준편차를 제곱(stdev(coffee)**2)해주거나 아래와 같이 해도 된다.

from statistics import variance
import numpy as np

coffee = np.array([202,177,121,148,89,121,137,158])
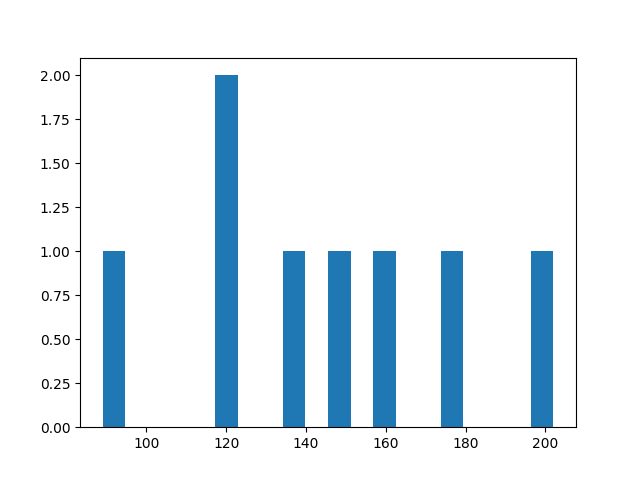
cf_var = variance(coffee)

실습✍ 수치형 자료의 요약 - 히스토그램

• 답안 작성하기 : plt.hist(coffee)

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from elice_utils import EliceUtils 
elice_utils = EliceUtils()

# 카페인 데이터
coffee = np.array([202,177,121,148,89,121,137,158])

fig, ax = plt.subplots()

"""
1. 히스토그램을 그리는 코드를 작성해 주세요
"""

plt.hist(coffee)


# 히스토그램을 출력합니다.
plt.show()
fig.savefig("hist_plot.png")
elice_utils.send_image("hist_plot.png")

• 결과
  
  x축은 카페인 함량 범위, y축은 해당 개수

🎈 Tips! : plt.hist(coffee, bins=20)
bins란 히스토그램을 구성하는 계급의 개수를 의미!! bins가 없으면 자동으로 계급을 나눠서 그림을 그리게 된다.