[Week 7] JSIS3D

3D 데이터셋의 고질적인 문제: large-scale, noisy data

이 페이퍼는 Point-based approach를 적용함. 이유는?

• Compact representations
• 잘 돼서..

하여튼 이 논문의 contributions 는 두개임:

1. Multi-Task Pointwise Network

즉, 3D points 의 카테고리를 예측한 뒤, 그 point 를 고차원의 feature vector 에 embedding 해서 clustering 기법을 활용함.

2. Multi-value conditional field

클라스 라벨과 객체 인스턴스를 한 framework 안에서 최적화 할 수 있게 해줌. Variational mean field 로 해결한다는데... 나중에 봐보자.

Related Works

1. Conditional Random Fields

2. Instance Segmentation

2D 에서는 bounding box 를 추출한 다음에 그 box 안에서 foreground 와 background 를 가려내는 마스크를 찾아냈음. 이 접근은 3D 데이터셋에서는 유효하지 않아 보이는데, 아마 바닥부터 훈련하지 않고 추출된 features 에서 객체를 탐지하기 때문이라고 (??) 함.

따라서, semantic segmentation framework 에서 object instance 를 제안하는 과정을 추가하는 전략을 도입해야 함. 최근엔 semantic map 을 학습한 뒤에 PointNet 으로 추출한 point features 사이의 유사도를 사용한 방법론이 제안되었으며, 이를 통해 비슷한 점을 하나의 instance 로 묶는데 성공하였음.

Proposed Method

먼저, 3D point cloud 전체를 겹쳐지는 3D window 를 사용해 스캔함. 각 window (꼭짓점과 함께) 는 신경망을 통해 꼭짓점의 semantic class label 을 유추하며 고차원 벡터에 embedding 됨. 이를 위해 저자들은 multi-task pointwise network (MT-PNet) 을 고안함. MT-PNet 의 목적은:

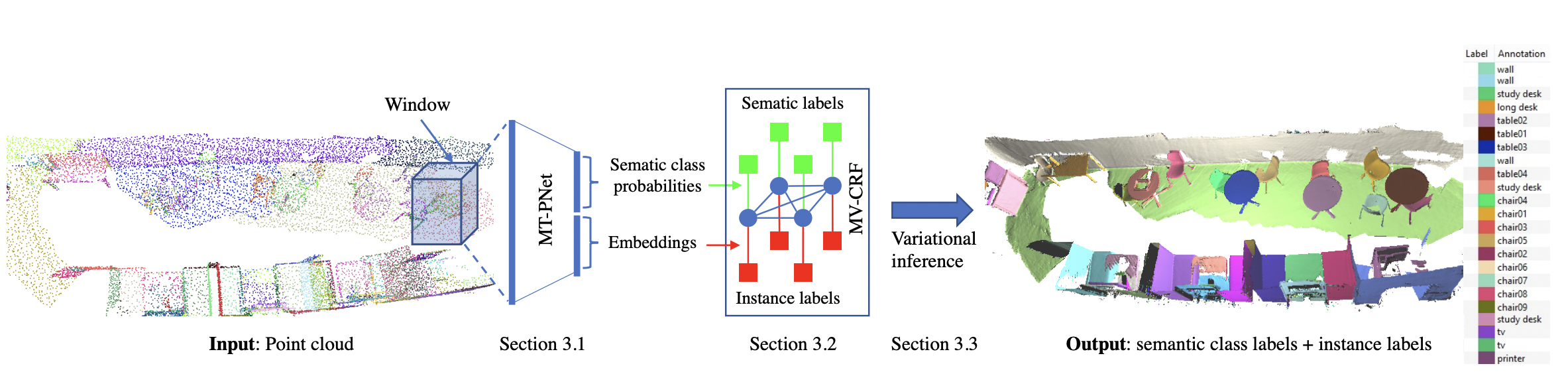
1. 모든 점에 대해서 클래스를 유추, 동시에 고차원 벡터에 임베딩

이 때, 비슷한 인스턴스들은 가까이, 다른 인스턴스들은 멀어지도록 임베딩 하려고 함

2. 클라스 라벨과 임베딩을 multi-value conditional random field (MVCRF) 에 넘김

MVCRF 모델에서 semantic / instance segmentation 이 variational inference 를 통해 함께 수행됨.

MT-PNet

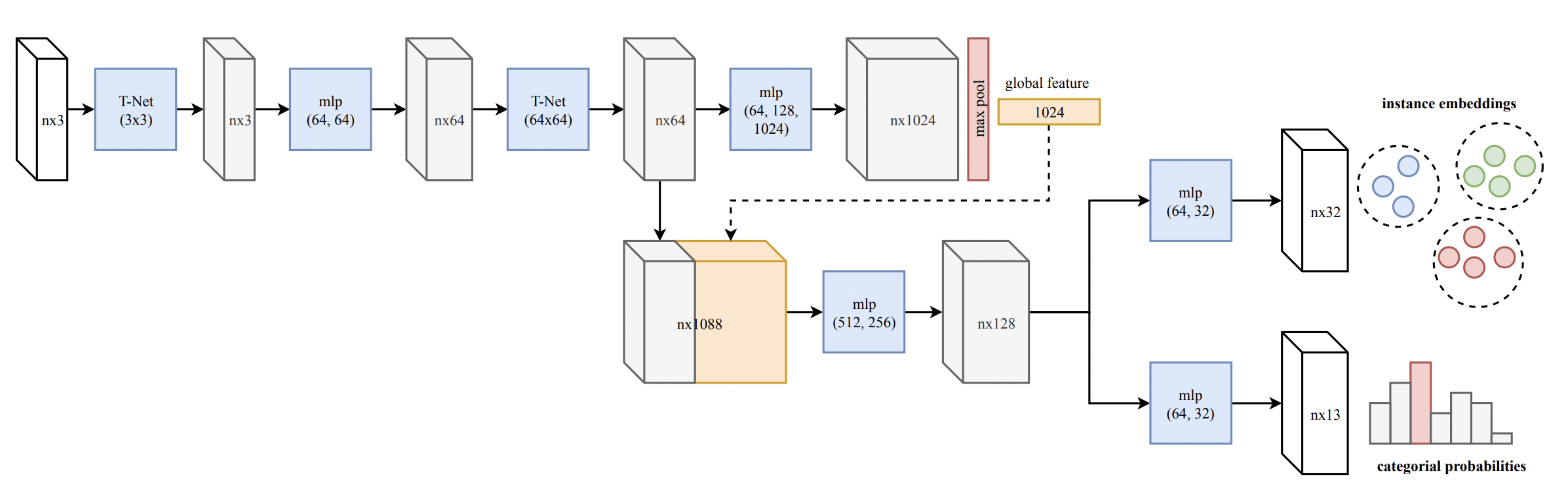
MT-PNet 의 구조는 대부분 PointNet 에서 따라옴.

먼저, N 개의 점을 가진 point cloud 에서 각각 D 만큼의 features 를 생성함. (N x D)

그 뒤, 윗단은 각 점을 고차원에 임베딩해주고, 아랫단은 semantic label 을 유추하게됨. 여기서 각 단에서 loss 를 정의할 수 있음

$L = L_{prediction} + L_{embedding}$

이 때, $L_{prediction}$ 은 cross-entropy, $L_{embedding}$ 은 discriminative loss (!!!) 사용.

MV-CRF

Notations 부터 확실하게..

$V=\{{v_1},...,{v_n}\}$ 은 3D reconstruction 이후의 vertex. 각 vertex 는 position, normal, 그리고 color 정보가 담겨있음
$L^S=\{{l_1^S},...,{l_N^S}\}$ 는 semantic label
$L^I=\{{l_1^I},...,{l_N^I}\}$ 는 instance label

S 는 정해져 있고 I 는 indeterminate 하다는 것을 기억하자.

여기서 arbitrary 한 두 vertex ${v_j}, {v_k}$ 가 undirected edge 로 연결되어있다고 가정하자. 각 vertex 의 semantic label 과 instance label 은 ${l_j^S}, {l_j^I}$ 로 나타날 것임.

여기서 $V, L^S, L^I$ 는 각 vertex $v_j$가 $({l_j^S}, {l_j^I})$ 와 연결되어있는 graph의 형태를 띄며, 이를 Multi-Value Conditional Random Field 라고 지칭한다.

우리의 목표는 $v_j$ 가 주어졌을 때, 그 instance의 $l^S_j$ 와 $l^I_j$ 를 때려맞추는것이므로, 다음의 energy function 을 최소화 하는 것을 목표로 한다:

어...

Unary potential, semantic labels

${\phi(l_j^S=s)}\propto-{\log{p(v_j|l^S_j=s)}}$

즉 ${v_j}$ 의 semantic label 을 s 라고 예측할 확률에 log 를 씌운 것이다 (만약 의자일 확률을 1이라고 예측한다면 0이 되는 것이며, 그보다 작은 경우 0보다 커질 것임)

Pairwise potential, semantic labels

저자들은 비슷한 카테고리의 object 들이 비슷한 classification distribution 을 가지고 있는 것을 관찰했으며, ${v_j}$ 와 ${v_k}$ 의 pairwise potential 을 제시함

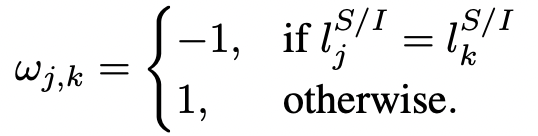
다시 한번 강조하지만, 작을 수록 좋다.

case 1: semantic label 이 다르고 (w=1) 확률 분포가 다름.

확률은 [0, 1] 의 값을 가지므로 두 확률의 차이의 제곱 또한 [0, 1] 사이임. 확률 분포의 차이가 클 수록 exp 값이 작아지며, ${\phi(l_j^S, l_k^S)}$ 의 값은 작음. Good!

case 2: semantic label 이 같고 (w=-1) 확률 분포가 비슷함.

확률 분포의 차이가 작을 수록 분자는 0에 가깝게 되며, exp 값은 1에 가까이 나옴. w 는 -1 이기 때문에 phi는 -1 가까이 됨. Good!

case 3: semantic label 이 다르지만 (w=1) 확률 분포가 비슷함.

확률 분포의 차이가 비슷하기 때문에, exp 값은 0에 가까워짐. 따라서, phi는 1에 가까워짐. Bad!

case 4: semantic label 이 같지만 (w=-1) 확률 분포가 다름.

확률 분포의 차이가 크기 때문에, exp 값은 1보다 작아짐. 따라서, phi는 -1 보다 큼. Bad!

Unary potential, instance labels

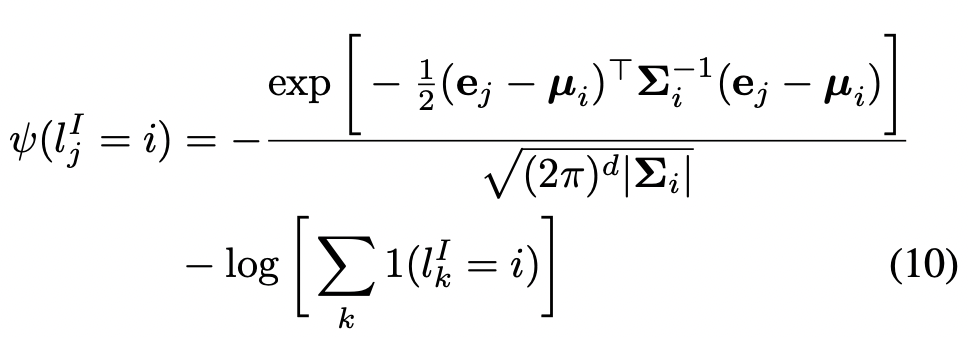
익숙하다면 정답이다. Gaussian Mixture 의 multi-modal probability density distribution 을 그대로 가져왔다.

간단히 말하자면, 여러개의 instance distribution 이 있을 때, 특정한 vertex 를 가장 근접한 gaussian 에 매핑하도록 하는 것을 목표로 한다.

Pairwise potential, instance labels

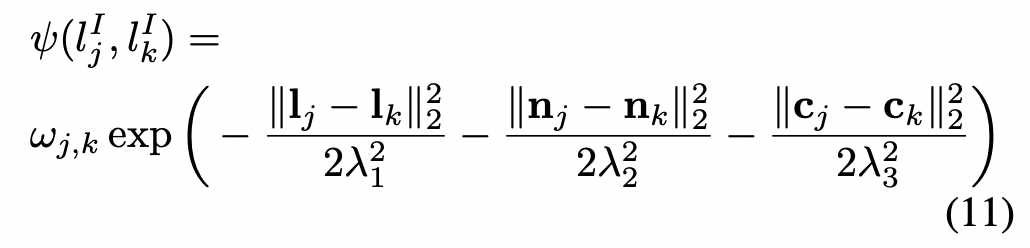
마찬가지로 같은 instance 들은 비슷한 gaussian 에, 다른 instance 는 다른 gaussian 에 매핑하는 것을 목표로 한다.

Semantic-instance potential

${\phi(s,i)=-h_i(s)\log{h_i(s)}}$

${\log{h_i(s)}}$ 는 특정 instance i 에서 class s 가 몇번 발생하는지이다. Point 10개가 있다고 가정할 때,

- ( 9 * log(9) + 1 * log(1) ) = -8.59
- ( 10 * log(10) ) = -10

즉, class 하나에 몰빵하는 것이 entropy 가 더 낮다.

Variational Inference

Posterior probability ${p(L^S, L^I|V)}$ 를 계산하는 것이 불가능하므로,

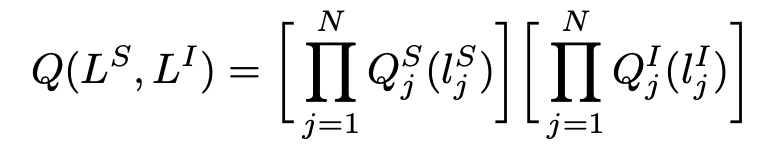
로 근사하려고 함. 이 때, L^S, L^I 는 독립이라고 가정했음.