🚨 이 글은 이 문제의 풀이와 정답 코드를 소개하는 글이 아니다! 🚨
이 문제를 정확히 이해하기 위해
1) 필요한 사전 지식
2) 문제 뜯어보기
를 정리한 글이다 🤓

행렬 곱셈 순서는 유명한 DP 문제이다.
그래서 알고리즘 스터디에 추천했는데 나에겐 문제를 이해하는 것부터 너무 어려웠기에,,
문제를 완벽히 이해하기 위해 했던 삽질을 잘 정리해서 스터디에서 발표 자료로 쓰려고 한다.
겉핥기로 이해하고 넘어갈까 했지만 행렬 관련 문제를 또 마주쳤을 때 이러한 개념들을 확실히 알고 있으면 좋을 것 같았다!

1. 행렬 곱셈

행렬 곱셈을 직접 해야 하는 문제는 아니지만, 행렬 곱셈에 대한 이해가 필요한 문제이다.
따라서 문제 이해에 필요한 행렬 곱셈 개념을 정리해보겠다.

1.1. 행렬 곱셈 방법

행렬 곱셈, 그거 어떻게 하는 거였더라..? 싶다면 아래 사진을 참고하자.
(행렬 및 행렬 곱셈에 대해 아예 무지하다면 구글링을 하는 것이 좋을 것이다!)

1.2. 행렬 곱셈의 조건

행렬 곱셈의 조건은 행렬 A와 B를 곱할 때 A의 열의 개수와 B의 행의 개수가 같아야 한다는 것이다.

* 앞으로 한 행렬의 사이즈를 nxn으로 표현하겠다.

• 2x3 * 3x5 => 가능
• 2x3 * 2x3 => 불가능

이는 행렬 곱셈의 방식을 생각해보면 금방 이해할 수 있는 조건이다.
(= 이 조건을 충족하지 않는다면 곱셈을 할 수 없다는 것을 금방 이해할 수 있다.)

참고로 axb 크기의 행렬과 bxc 크기의 행렬을 곱하면 axc 크기의 행렬이 된다. ⭐️
이 또한 행렬 곱셈의 방식을 생각해보면 자명한 사실이다.

1.3. 행렬 곱셈의 성질

• 행렬 곱셈의 교환법칙은 성립하지 않는다. AB !== BA
  => 위의 행렬 곱셈의 조건과 같은 맥락이다.

• 행렬 곱셈의 결합법칙은 성립한다. A(BC) = (AB)C
  => 곱셈 결과 행렬의 크기가 정해지는 규칙을 생각해보면 된다. 어떤 두 행렬을 먼저 곱하든 결국 제일 첫번째 행렬의 행의 개수가 결과 행렬의 행이 되고 마지막 행렬의 열의 개수가 결과 행렬의 열의 개수가 될 것이다.

2. 문제 이해하기

문제에서 요구하는 바는 곱셈을 해서 결과값을 얻고자 하는 것이 아닌,
여러 개의 행렬을 곱할 때, 곱셈 순서에 따라 달라지는 곱셈 연산의 개수의 최솟값이다.

이것을 조금 풀어서 써보면 아래와 같다.

1. 여러 개의 행렬을 곱할 것이고,
2. 그들을 다양한 순서로 곱할 수 있으며,
3. 그에 따라 곱셈 연산의 개수가 달라지는데,
4. 결론: 그 여러 곱셈 연산의 개수 중 최솟값이 무엇인가?

아직도 이해가 완벽히 되지 않을 수 있다. (내가 그랬다..!)
아래에서 위 각각의 항목에 대해 자세히 살펴보겠다.

2.1. 곱셈 순서

일단, 여러 행렬을 다양한 곱셈 순서로 곱할 수 있다는 것이 전제이다.
이것이 성립하는 이유는 위에서 설명했던 행렬 곱셈의 성질 중 결합법칙 때문이다.
예를 들자면 A(BC)와 (AB)C 중 어떤 것이 연산의 개수가 적어질 것인지 묻는 것이다.
이 순서의 따라 곱셈 연산의 개수가 달라진다.

이해를 돕기 위해 <다양한 곱셈 순서>에 대해 다르게 말하자면,
'행렬 곱셈 식에서 괄호를 어떻게 칠 것인가'가 될 수 있다.
위에서 든 예시처럼 ABC는 A(BC)와 (AB)C 두 가지 방법으로 괄호를 칠 수 있다.
이에 따라 곱셈 순서는 두 가지로 달라진다.

1. (AB)C
   1) A * B
   2) A*B의 결과 * C
2. A(BC)
   1) B * C
   2) A * B*C의 결과

당연하지만 위 두 순서만 다른 곱셈의 결과는 같을 것이다.

2.2. 곱셈 연산

그렇다면 과연 문제에서는 곱셈 연산이란 정확히 어떤 연산을 말하는 것이며, 곱셈 연산의 개수가 어떤 식으로 달라질까?

2.2.1. 문제에서 말하는 <곱셈 연산>이란?

문제에서 곱셈 연산은 아래 행렬 곱셈에서 노란색 네모 하나 하나를 말한다.

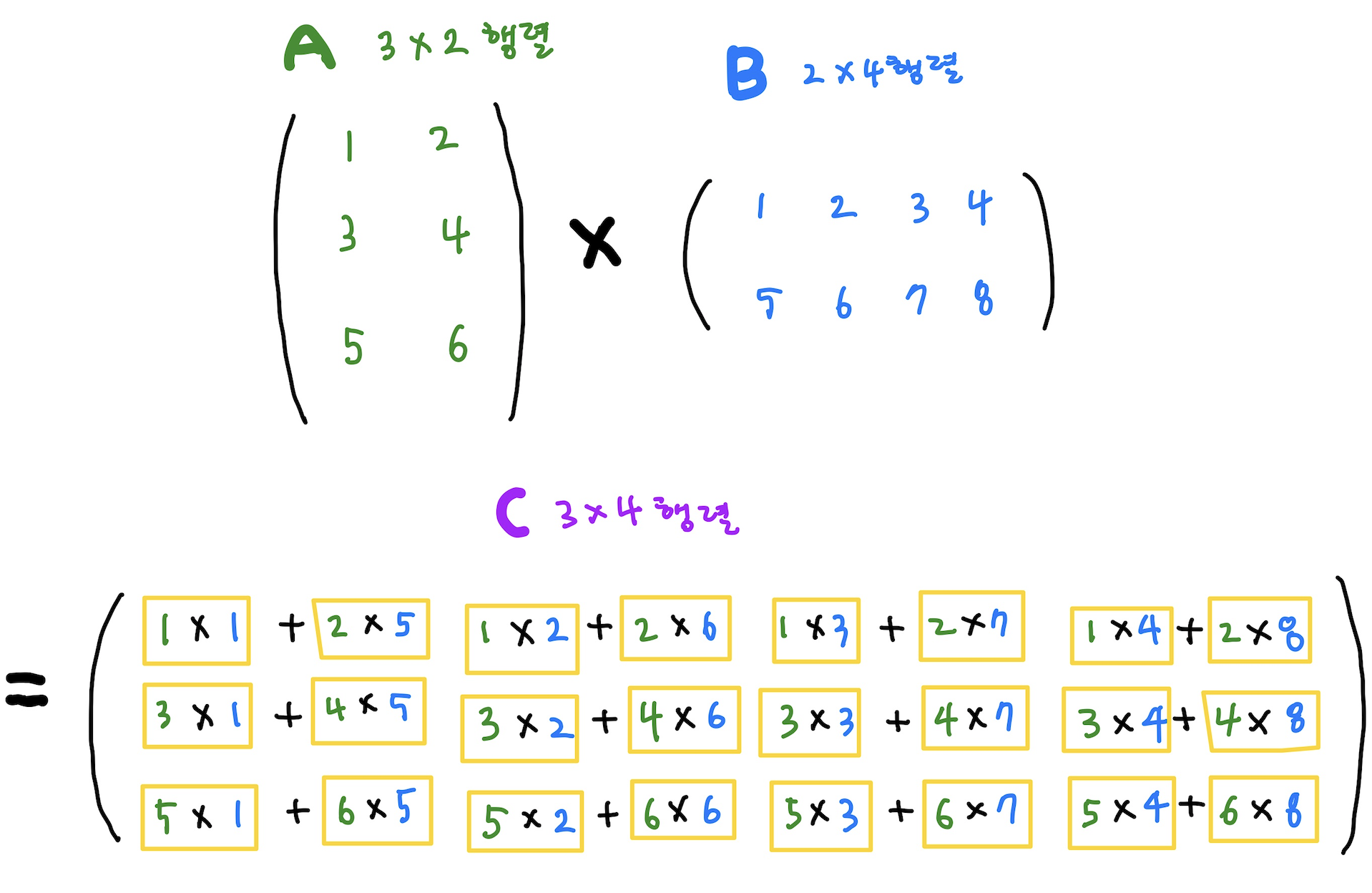
여기서 곱셈 연산의 개수는 24개이다.

2.2.2. 곱셈 연산의 개수

곱셈 연산의 개수는 A 행렬과 B 행렬을 곱할 때 아래와 같다.

A의 행의 개수 * B의 열의 개수 * A의 열의 개수(=B의 행의 개수)

따라서 아래 행렬 곱셈의 경우 곱셈 연산의 개수는 2 * 2 * 3이 될 것이다.

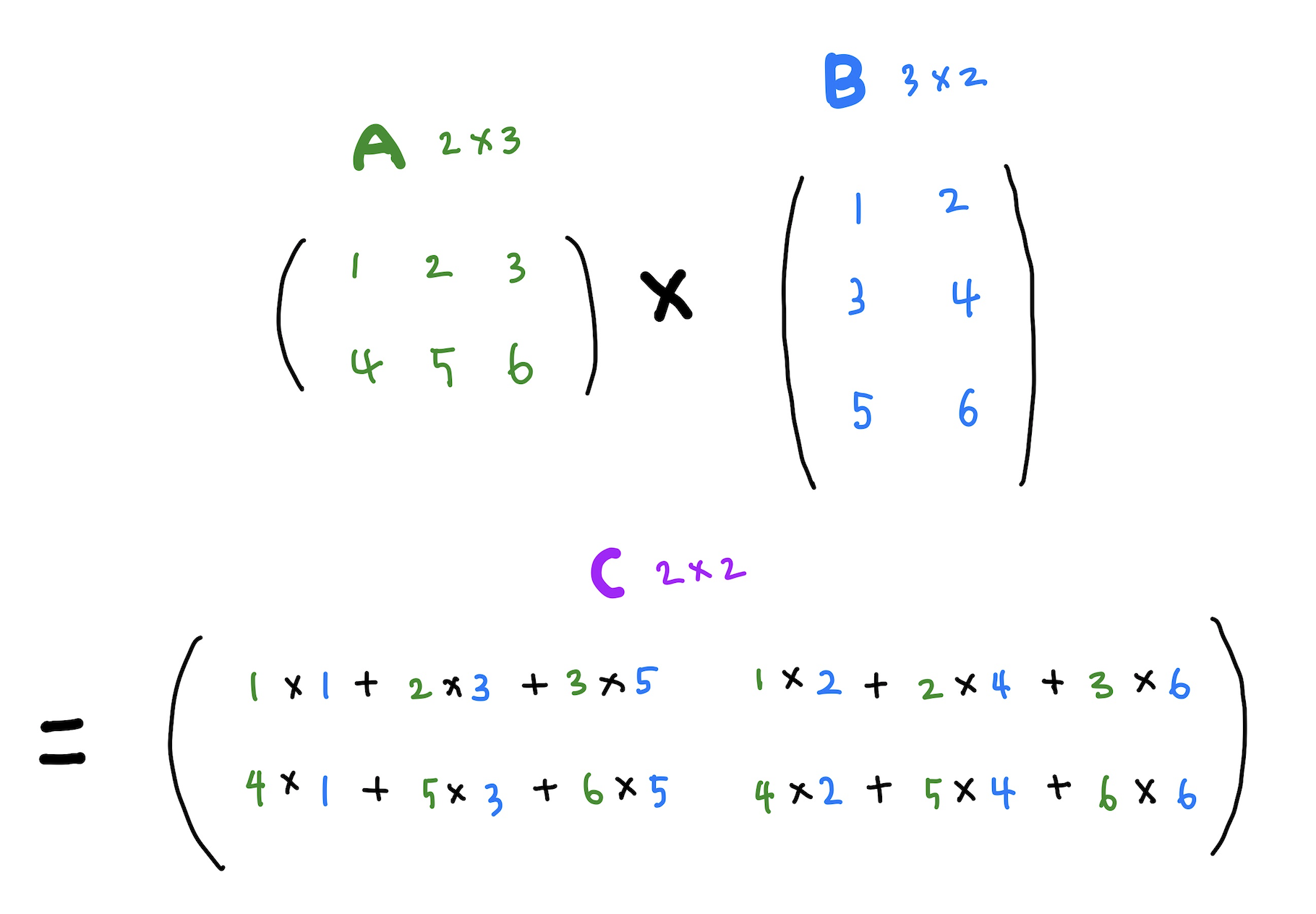
왜일까?

1. C의 한 원소의 값을 얻기 위해서는 일단 A의 열의 개수(=B의 행의 개수)만큼의 곱셈 연산을 해야한다.
   이것을 C의 총 원소의 개수만큼 하게 될 것이다.
   => C의 총 원소의 개수 x A의 열의 개수(=B의 행의 개수)

2. C의 총 원소의 개수는 C의 행의 개수 x C의 열의 개수이다.
   => C의 행의 개수 x C의 열의 개수 x A의 열의 개수(=B의 행의 개수)

3. 위의 1.1.에 따르면 C의 행의 개수 x C의 열의 개수는 곧 A의 행의 개수 x B의 열의 개수이다.
   => A의 행의 개수 x B의 열의 개수 x A의 열의 개수(=B의 행의 개수)

이에 따라 결국, AB의 곱셈 연산 개수는 A의 행의 개수 x B의 열의 개수 x A의 열의 개수(=B의 행의 개수)이 되는 것이다.

2.2.3. 곱셈 연산 개수의 변화

이제 곱셈 연산의 개수가 곱셈 순서에 따라 달라지는지 예를 들어 보여주겠다.

아래 세 행렬이 있다고 하자.

A: 2x5
B: 5x3
C: 3x4

이들 행렬을 (AB)C, A(BC) 두 순서로 곱했을 때의 곱셈 연산 개수를 보겠다.

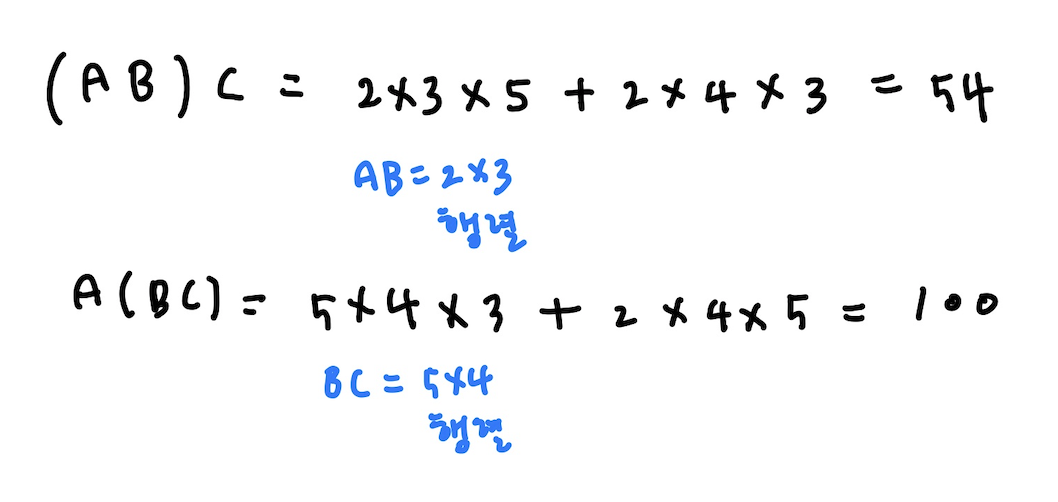
이렇게 결합법칙이 성립함에 따라 어떤 순서로도 곱할 수 있지만,
각기 다른 곱셈 과정에서 곱셈 연산 개수 공식인 A의 행의 개수 x B의 열의 개수 x A의 열의 개수(=B의 행의 개수)에 들어가는 각각의 숫자가 달라진다.
그래서 곱셈 순서에 따라 곱셈 연산의 개수가 달라지는 것이다.

---

앞에서 말했듯이 이 글에서 문제 풀이는 다루지 않겠지만 핵심 포인트를 얘기하자면 다음과 같다.

곱하는 행렬의 개수가 많아질수록 곱셈 연산의 개수의 경우의 수가 어마어마해질 것이다.
따라서 이 경우의 수를 DP를 이용해 저장(Memoization)을 하며 최솟값을 찾아내는 것이 이 문제의 해법이 되는 것이다!