본 게시글은 주재걸 교수님의 인공지능을 위한 선형대수 강의를 듣고 정리한 내용입니다.
https://www.boostcourse.org/ai251/joinLectures/195088
Notation
Scalar : 소문자
Vector : 굵은 소문자 (기본 형태가 column vector)
Matrix : 대문자
핵심
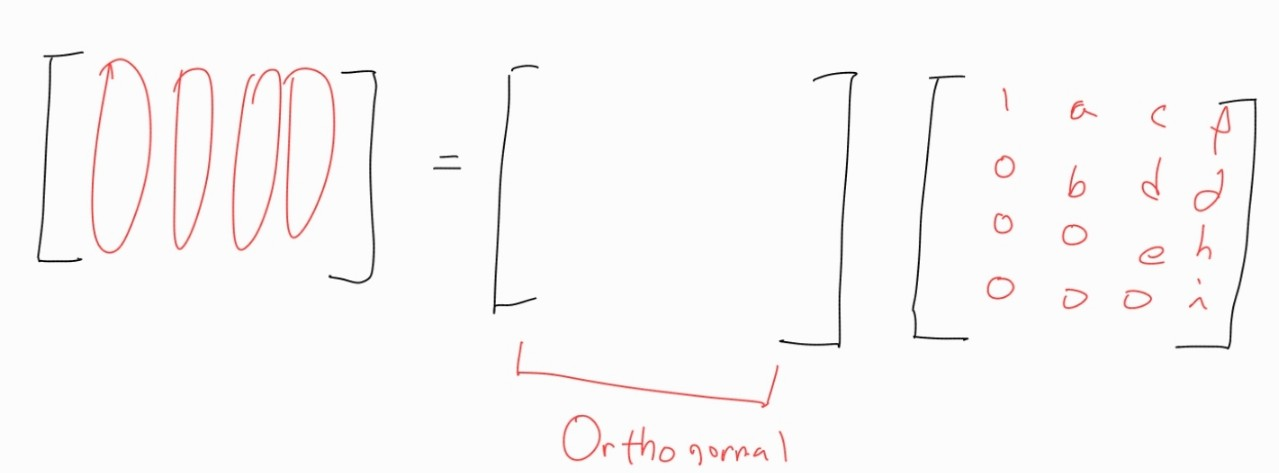
- 임의의 행렬을 Orthogonal 한 행렬과 선형결합 계수 행렬의 곱으로 바꾸기
전 시간에 컬럼 벡터들이 서로 유사할 경우에 어떤 불이익을 가지는지 살펴보았다.
이 방법의 필요성을 다시 상기하기 위해 다시 비슷한 예제를 살펴보자.
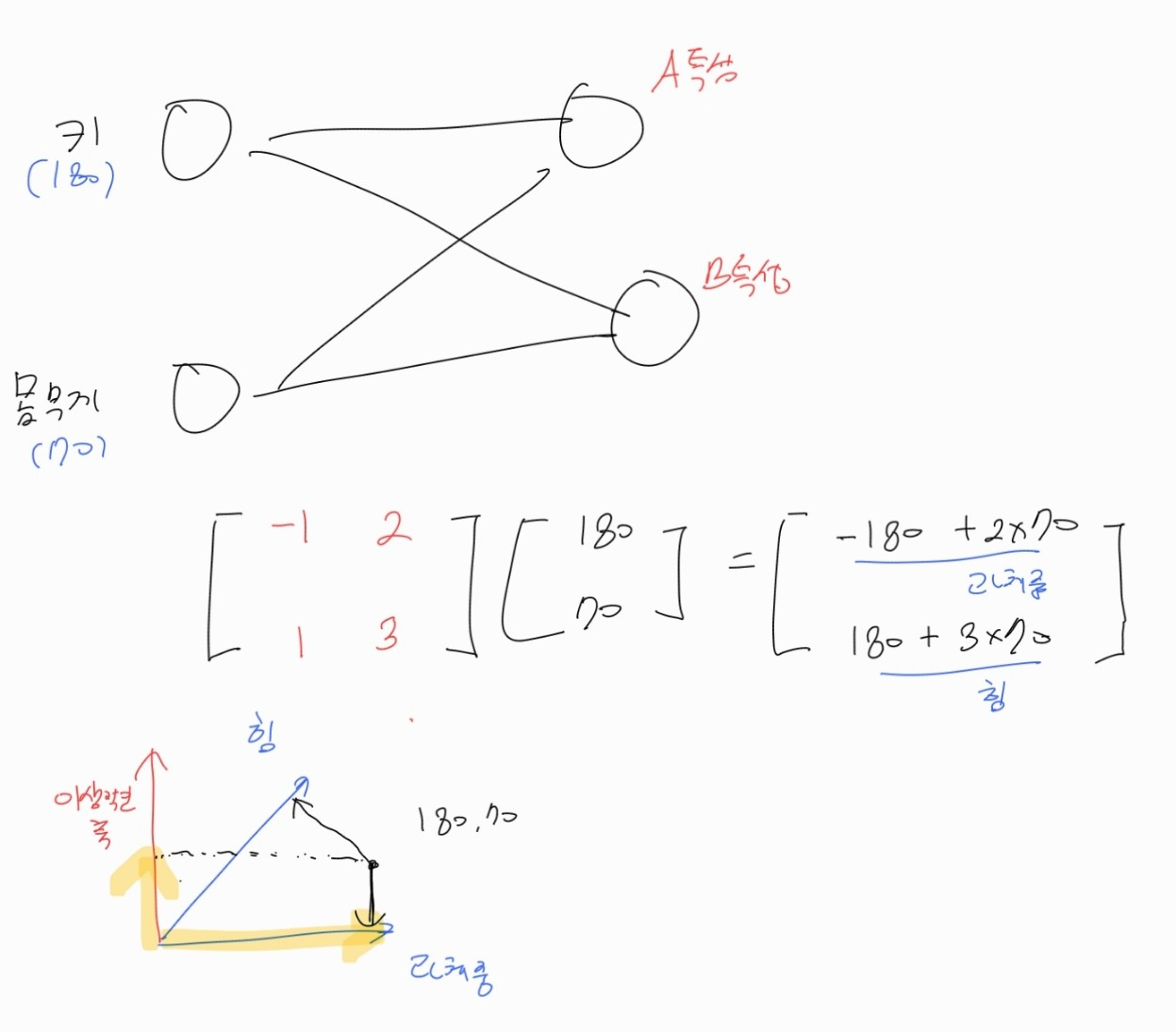
위와 그림에서 뽑아진 힘과 과체중 벡터는 유사한 의미를 담게 된다. 이 정보들은 각각 정보 추출 행렬의 row 벡터로부터 뽑아진다.
위 그림처럼 정보 추출 행렬의 row 벡터가 유사한 정보를 담게되는 것 보다 서로 다른 정보를 추출하는 것이 모델의 안정성에 도움이 된다. 다중공선성 문제와도 연결되기도 한다.
즉, 이렇게 추출한 feature간의 의미 중복을 피하기 위해서는 추출 행렬의 row 벡터를 모두 서로 직교 벡터로 만드는 작업이 필요하다.
Gram-Schmidt Orthogonalization
임의의 행렬을 Orthogonal 한 행렬과 계수 행렬의 곱으로 쪼개는 방법이다.
방법은 간단하다.
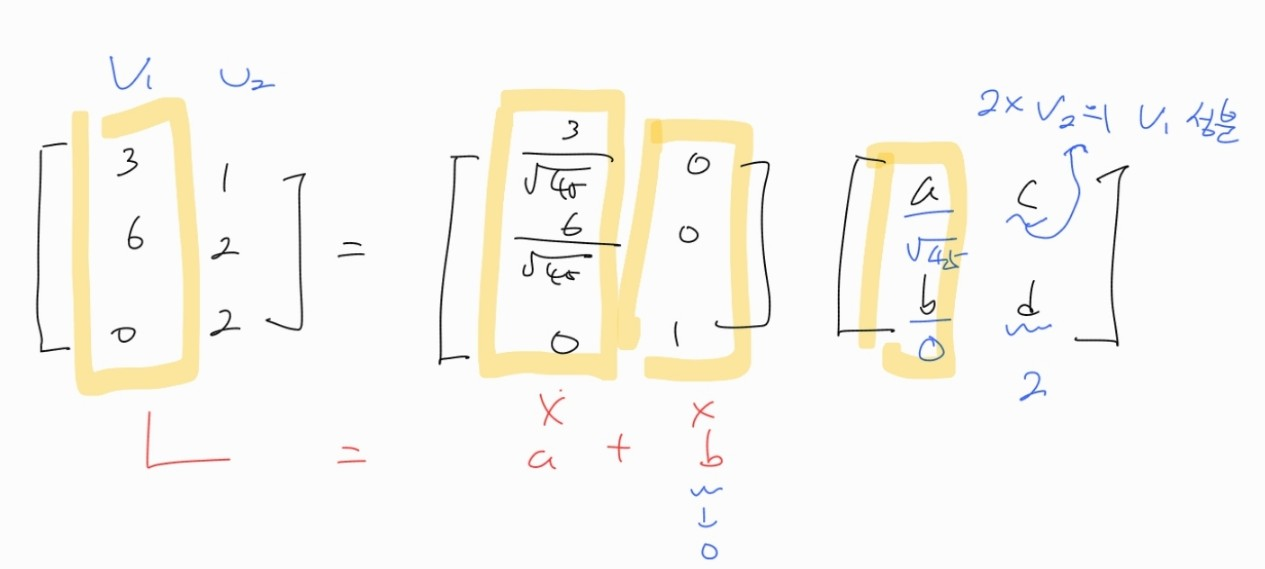
우선 우리가 쪼개고자 하는 행렬이 3 x 2 일 경우 2개의 열벡터를 가진다. 우선 Orthogonal한 벡터를 만들기 위해 첫 번째 벡터를 길이를 1로 만들어서 가져오고, 두 번째로 들어오는 벡터는 첫 번째 벡터에 수직하게 가져온다.
수직하게 만드는 방법은 기존 벡터 성분을 제거하면 된다.
이렇게 되면 임의의 행렬은 각 Orthogonal 한 벡터들의 선형 결합으로 이루어지는데, 이때 선형결합의 계수를 나머지 하나의 행렬로 채운다.
선형결합의 계수를 나타내는 행렬은 자연스럽게 2 x 2 정방행렬이 나오게 된다.
Q-R Factorization
앞서 Gram-Schmidt Orthognalization을 통해서 우리는 열벡터끼리 직교하는 행렬과 선형결합 계수 행렬의 곱으로 쪼갰는데, 이 과정이 Q-R Factorization 이다.
만약 Gram-Schmidt 방법을 사용했다면 계수 행렬은 하삼각행렬이 된다.