10. Orthogonal Projection

본 게시글은 주재걸 교수님의 인공지능을 위한 선형대수 강의를 듣고 정리한 내용입니다.
https://www.boostcourse.org/ai251/joinLectures/195088

Notation

Scalar : 소문자
Vector : 굵은 소문자 (기본 형태가 column vector)
Matrix : 대문자

핵심

• Orthogonal Projection의 개념 : 정사영
• Orthogonal Sets : 직교 (원소끼리 모두)
• Orthonormal Sets : 직교하는데 길이가 모두 1
• Orthogonal이 필요한 이유
  • 특성을 뽑아내는 weight matrix의 열벡터가 서로 수직이 아닌 유사한 방향일 경우 의미가 중복되어 overfitting 및 학습 저해

Orthogonal Projection의 개념

우리는 이전까지 Least Sqaure Problem을 푸는 방법으로 정규방정식을 살펴보았다.

$(A^TA)\hat \bold x = A^T\bold b$

그 결과 A가 역행렬이 존재하면 해는 다음과 같이 나타낼 수 있다.

$\hat \bold b = f(\bold b) = A\hat \bold x = A(A^TA)^{-1}A^T\bold b$

$\hat \bold b$ 의 의미를 다시 한 번 상기시켜보면 $\bold b$가 col A에 Orthogonal Projectio, 즉 정사영된 벡터이다.

임의의 $\hat \bold b$는 A의 열벡터들의 선형결합으로 나타내어지고 $\hat \bold b$가 존재할 수 있는 공간은 A의 열벡터들이 만들어내는 공간이다.

우리가 원하는 것은 $\bold b$와 거리가 최소가 되는 $\hat \bold b$을 찾는 것이고, 이는 col A에 $\bold b$가 내린 수선의 발이다.

즉 다시 말해 $\hat \bold b = A(A^TA)^{-1}A^T\bold b$ 에서 $A(A^TA)^{-1}A^T$ 연산은 col A에 어떤 벡터를 Orthogonal Projection(정사영)해주는 선형변환이 되며, $\hat \bold b$는 정사영된 벡터가 된다.

Orthogonal and Orthonormal Sets

Orthogonal sets는 원소 각각이 수직인 벡터를 의미한다. Orthonormal sets는 orthogonal 하면서 길이가 1인 것을 의미한다.

Orthogonal을 만족하면 당연히 선형독립이지만 역은 성립하지 않는다.

Orthogonal Projection onto Line, Plane

어떠한 점을 직선에 정사영 시키는 것은 내적과 벡터의 뺼셈을 이용해서 쉽게 구할 수 있다.

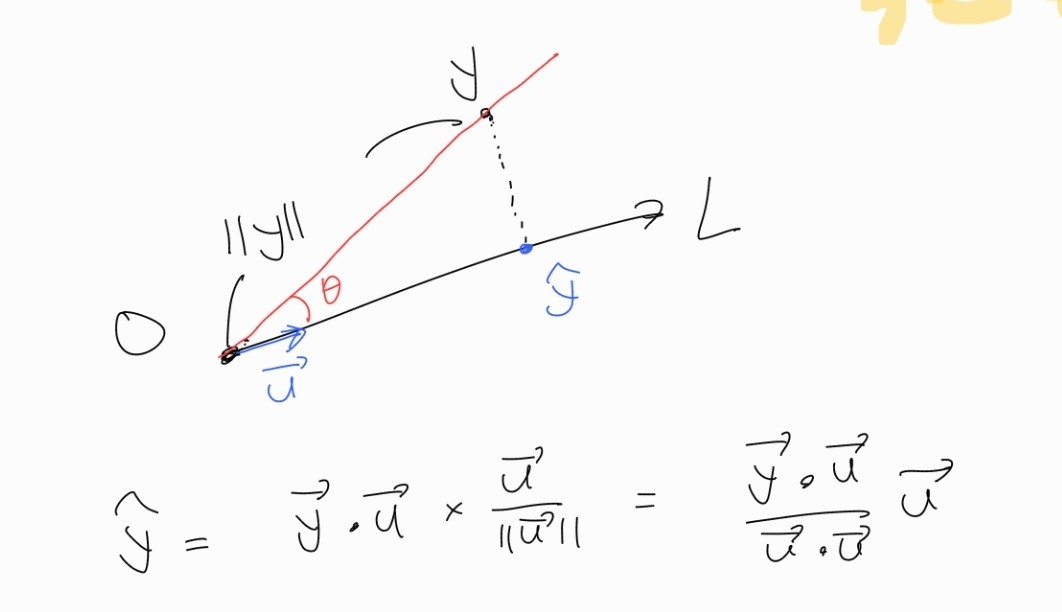
직선에 정사영 하는 방법을 이용해서 평면에도 마찬가지로 정사영을 내릴 수 있다.

이때 만약 두 벡터가 서로 수직이고 길이가 1 즉 orthonormal 하다면 다음과 같이 계산할 수 있다.

이러한 사실을 통해 알 수 있는 사실은 어떠한 span에 정사영하고 싶을 때 그 공간의 orthonormal basis를 찾는다면 각각의 basis vector에 정사영 한 후 더해주면 된다는 점이다.

위 식을 정리하면 다음과 같이 행렬곱으로도 나타낼 수도 있다.

Orthogonal이 필요한 이유

키와 몸무게로 힘을 측정하는 task가 있다고 해보자.

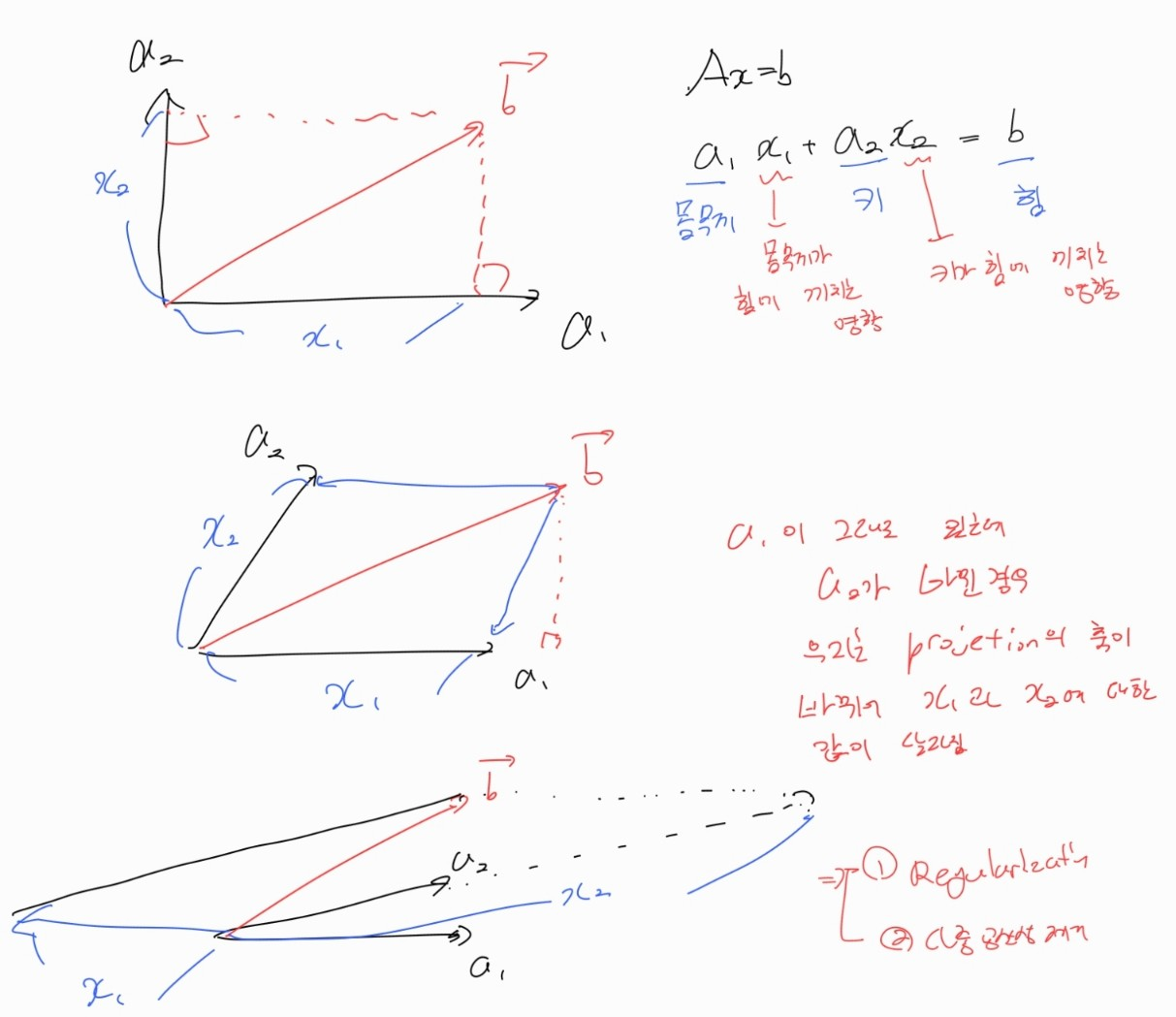
다음 그림과 같이 몸무게 벡터와 키 벡터가 바뀜에 따라 몸무게가 힘에 미치는 영향과 키가 힘에 미치는 영향이 바뀌게 된다.

맨 마지막 그림의 경우에는 몸무게와 키가 굉장히 상관관계가 높은 경우인데, 이렇게 되면 train data에 overfitting 되어 불안정한 모델이 학습된다.

아래는 조금 더 이해하기 쉽게 키를 근육량으로 바꿔본 간단한 예시다.

몸무게와 근육량으로 힘을 측정하는 task에서 몸무게와 근육량이 대체로 몸무게/2 = 근육량이 성립한다고 하면,
실제 이상적인 계수가 몸무게 x 1 + 근육량 x 2 = 힘이지만 학습 데이터에서는 에서 몸무게 x -1 + 근육량 x 6 = 힘으로 학습되어도 힘을 추정하는데엔 문제가 없다.

이런 경우 valid 나 test에서 조금만 이상치가 들어와도 근육량에 너무 민감한 모델이 되게 되고, 이는 overfitting이다.

이러한 문제를 해결하는 방법으로는 직접 상관관계가 높은 변수들을 제거하거나, 한 변수에 치중하지 않도록 Regularization을 거는 방법이 있다. (Ridge, Lasso 등등)

Ridge의 경우 동작하는 과정을 살펴보면 몸무게와 키 벡터들을 orthogonal하게 바꿔주는 역할을 한다.