13. 대각화

본 게시글은 주재걸 교수님의 인공지능을 위한 선형대수 강의를 듣고 정리한 내용입니다.
https://www.boostcourse.org/ai251/joinLectures/195088

Notation

Scalar : 소문자
Vector : 굵은 소문자 (기본 형태가 column vector)
Matrix : 대문자
Col A (Column space of A) : A의 열벡터들이 만드는 span
Row A (Row space of A) : A의 행벡터들이 만드는 span
Nul A (Null Space of A) : $A\bold x = 0$을 만족하는 x의 집합

핵심

• 대각화 $D = V^{-1}AV$
  • 조건 1. VD = AV 를 만족하는 V 존재
    • 이건 A의 고유벡터들로 V를 채우면 항상 가능
  • 조건 2. V의 역행렬 존재
    • A의 교유벡터들이 선형독립이면 가능

어떤 정사각 행렬을 대각행렬로 바꾸고자 했을 때 다음과 같이 식을 쓸 수 있다.

$D = V^{-1}AV$

여기서 만약 우리가 이를 만족하는 행렬 V를 찾는다면 대각화가 가능하다.

위 식을 조금만 변형하여 다음과 같이 써보자.

$VD = AV$

우리는 이 식을 만족하는 V를 찾고 만약 V가 역행렬이 존재한다면 맨 위의 식과 동일해지므로 대각화가 가능하다고 할 수 있다.

$VD = AV$ 이 식의 의미를 살펴보자.

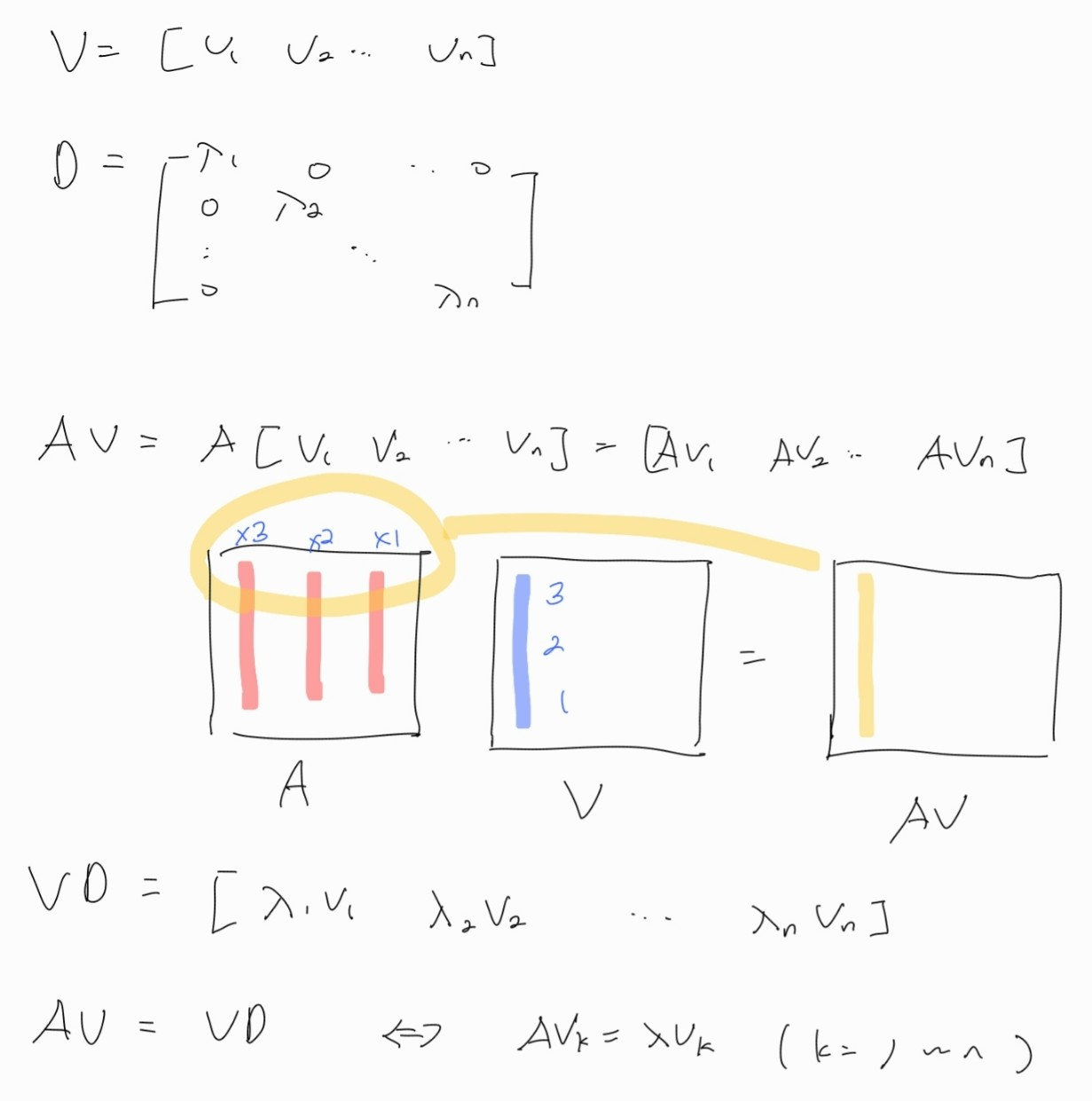
위에서 살펴보았듯 V를 A의 고유벡터로 채우게 되면 AV = VD 식을 만족시킬 수 있다.

이제 대각화를 하기 위해 V의 역행렬이 존재하는지에 대해 생각해보자.

이는 정사각행렬 A의 교유벡터들이 선형독립인지 아닌지에 따라 달려있다.