14. 고유값 분해와 선형변환

본 게시글은 주재걸 교수님의 인공지능을 위한 선형대수 강의를 듣고 정리한 내용입니다.
https://www.boostcourse.org/ai251/joinLectures/195088

Notation

Scalar : 소문자
Vector : 굵은 소문자 (기본 형태가 column vector)
Matrix : 대문자
Col A (Column space of A) : A의 열벡터들이 만드는 span
Row A (Row space of A) : A의 행벡터들이 만드는 span
Nul A (Null Space of A) : $A\bold x = 0$을 만족하는 x의 집합

핵심

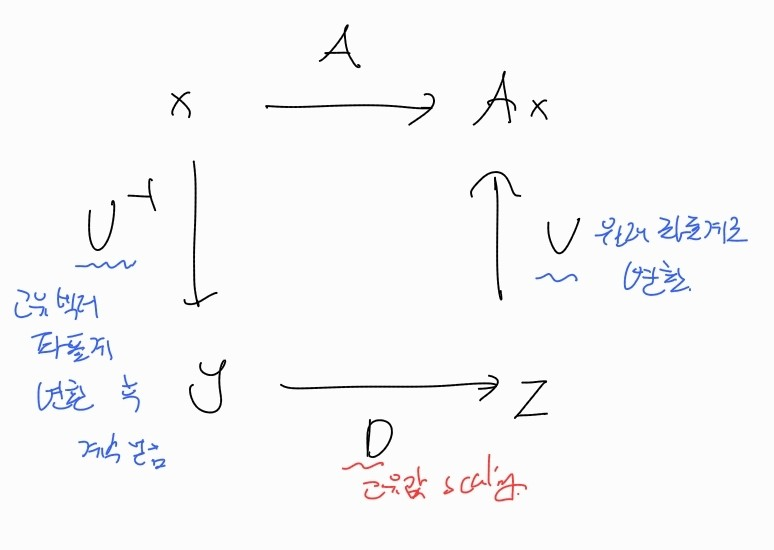
• 고유값 분해는 선형변환을 3단계의 변환으로 바꾸는 것이다.
  • 1. 고유벡터 좌표로 변환
  • 2. 고유값만큼 스케일링
  • 3. 원래 좌표로 변환

고유값 분해의 정의

지난 포스트에는 대각화에 대한 이야기를 했다.

만약 어떤 행렬 A가 대각화가 가능한 행렬이라면 우리는 고유값 분해를 시도해 볼 수 있다.

대각화가 가능한 A는 다음 식을 만족하는 A였다.

$D =V^{-1}AV$

이 식을 다시 A의 관점에서 써보면 다음과 같이 쓸 수 있다.

$A=VDV^{-1}$

우리는 현재 A라는 행렬을 3개의 행렬로 분해했다.

이러한 과정을 바로 고유값 분해라고 한다.

고유값 분해의 해석

우리는 왜 고유값 분해를 하려고 할까?

결론부터 말하자면 고유값 분해를 하면 고유벡터가 아닌 임의의 벡터 x에 대해 고유벡터처럼 계산할 수 있다.

우리는 이전에 선형변환 A에 대한 고유벡터는 x는 변환될 때 상수배만 곱해서 계산 이득을 얻는다는 것을 확인했다.

$A\bold x = \lambda \bold x$

이러한 일반적으로 연산은 x가 고유벡터일 때만 가능하다.

하지만 임의의 벡터를 고유벡터의 선형결합으로 나타낸다면 위와 같은 방식으로 계산을 할 수 있다.

위 과정이 어떤 순서로 무엇이 일어났는지 살펴보자.

1. 고유벡터가 아닌 입력값을 고유벡터의 선형결합으로 표현하기 위해 고유벡터 계수를 구함

2. 구한 고유벡터 계수에 교유값을 곱함

3. 고유벡터들에 계수들을 곱하여 더함

고유값 분해는 이와 동일한 과정을 행렬연산으로 하는 것이다.

$A\bold x = VDV^{-1}\bold x$

1. $V^{-1}\bold x$ 연산의 의미

이 연산은 입력값 x를 고유벡터의 선형결합으로 나타내기 위해 계수를 구하는 작업이다.

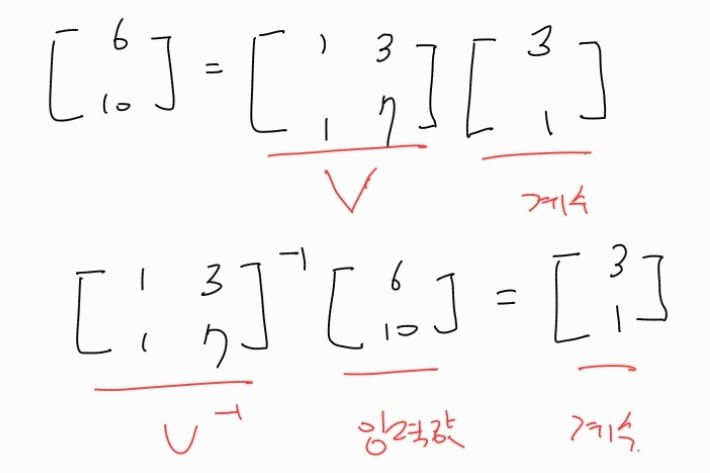
이 작업은 change of basis 개념으로도 볼 수 있다.
기준 축이 (0,1), (1,0) 이었던 벡터를 (1,1), (3,7)이 축인 공간으로 이동시킨 것이다.

즉, 고유벡터를 축으로 하는 공간으로 이동시켜 거기서의 좌표를 구했다고 생각하면 된다.

2. $DV^{-1}\bold x$ 연산의 의미

이 연산은 구한 고유벡터 좌표에 고유값만큼 스케일링 해주는 것이다. 여태 좌표를 바꿨다면 실질적인 변환은 여기서 일어난다고 볼 수 있다.

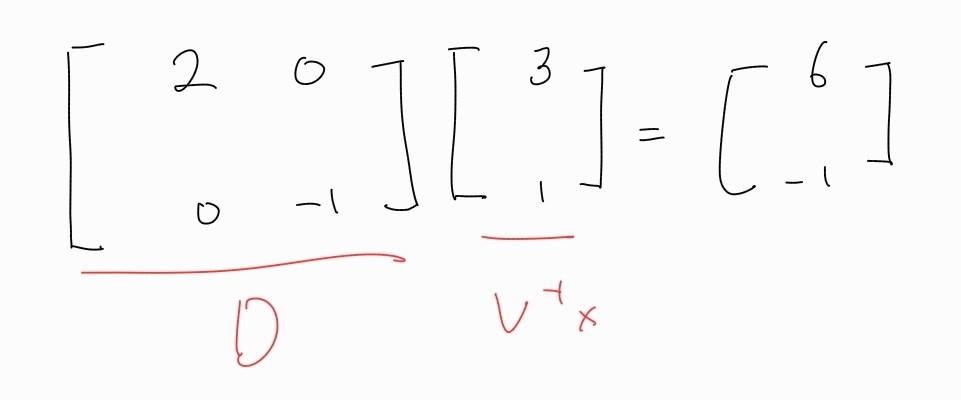
참고로 대각화가 가능한 행렬 A의 대각행렬의 원소는 각각 고유값이다.

3. VDV^{-1} 연산의 의미

이제 고유벡터 좌표계에서 원래 우리가 구하고자 하는 좌표계로의 변환을 의미한다.

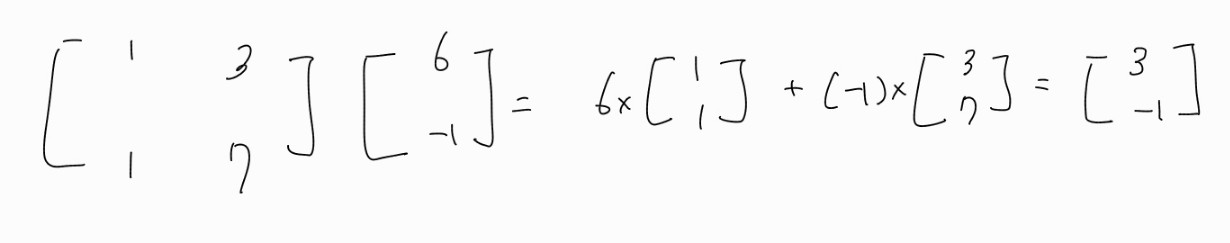
정리

고유값 분해는 임의의 입력값을 고유벡터의 선형결합으로 만든 후 연산하는 작업이고 다음과 같이 그림으로 나타낼 수 있다.