16. 고유값 분해와 특이값 분해의 응용

본 게시글은 주재걸 교수님의 인공지능을 위한 선형대수 강의를 듣고 정리한 내용입니다.
https://www.boostcourse.org/ai251/joinLectures/195088

Notation

Scalar : 소문자
Vector : 굵은 소문자 (기본 형태가 column vector)
Matrix : 대문자
Col A (Column space of A) : A의 열벡터들이 만드는 span
Row A (Row space of A) : A의 행벡터들이 만드는 span
Nul A (Null Space of A) : $A\bold x = 0$을 만족하는 x의 집합

핵심

• 고유값 분해
  • 주성분분석(PCA)
• 특이값 분해
  • Low-Rank Approximation
  • Dimension - Reducing Transformation

고유값 분해의 응용

대부분의 머신러닝 문제를 풀 때 우리가 고유값 분해를 이용하는 경우는 $A$ (feature - by - data item)에 쓰는게 아니라 다음과 같이 변형해서 쓴다.

$AA^T$ (feature - by - feature)

• feature 간의 내적값 -> 유사도의 의미를 가짐
• PCA -> feature간의 공분산행렬을 구한 후 고유값 분해를 이용해서 가장 분산이 큰 축 찾기

$A^TA$ (data item by - data item

• data item 간의 유사도

이 두 경우로 주로 사용하게 되는데, 둘 다 Symmetric positive definite matrics 이기 때문에 고유값 분해는 항상 가능하다.

특이값 분해의 응용

특이값 분해는 주로 정보의 손실을 최소화하며 행렬을 축약하는 형태를 띈다.

Low-Rank Approximation of a Matrics

이 방법은 주로 편향값이나 사소한 정보들을 제거하고 싶을 때 사용하는 방법이다.

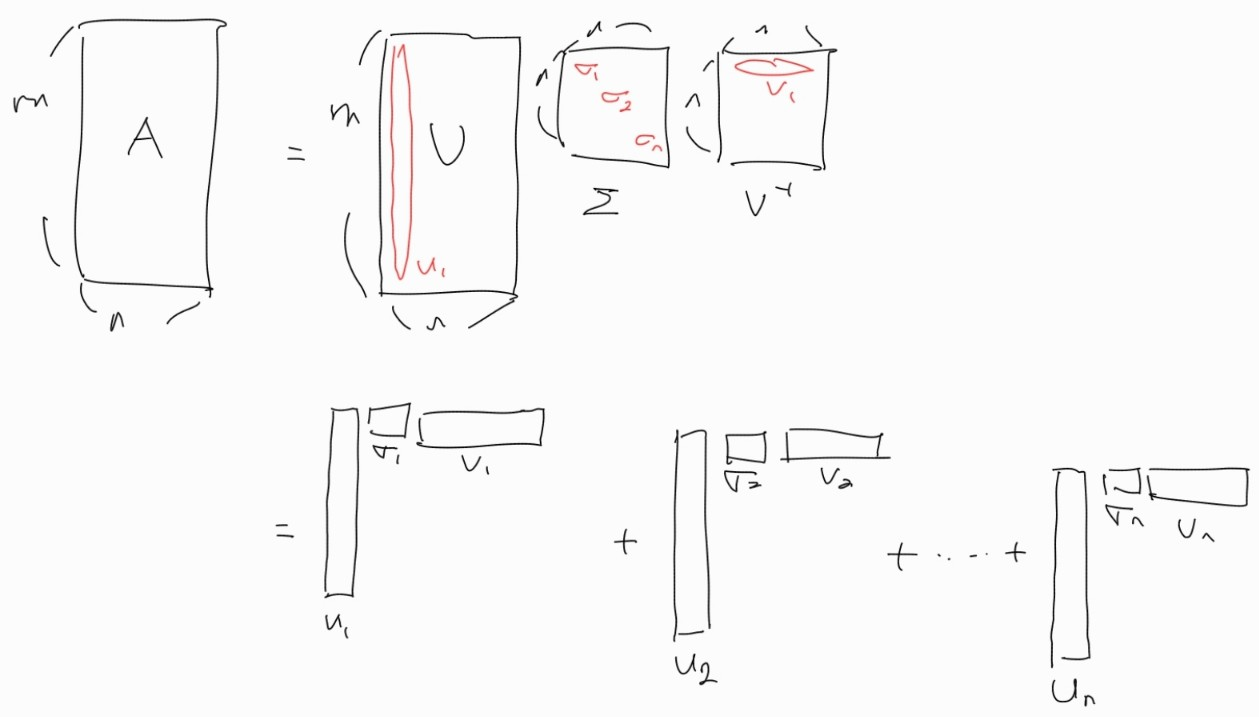
이 방법의 의미를 이해하기 위해 특이값 분해 행렬을 다음과 같이 외적으로 표현할 수 있다.

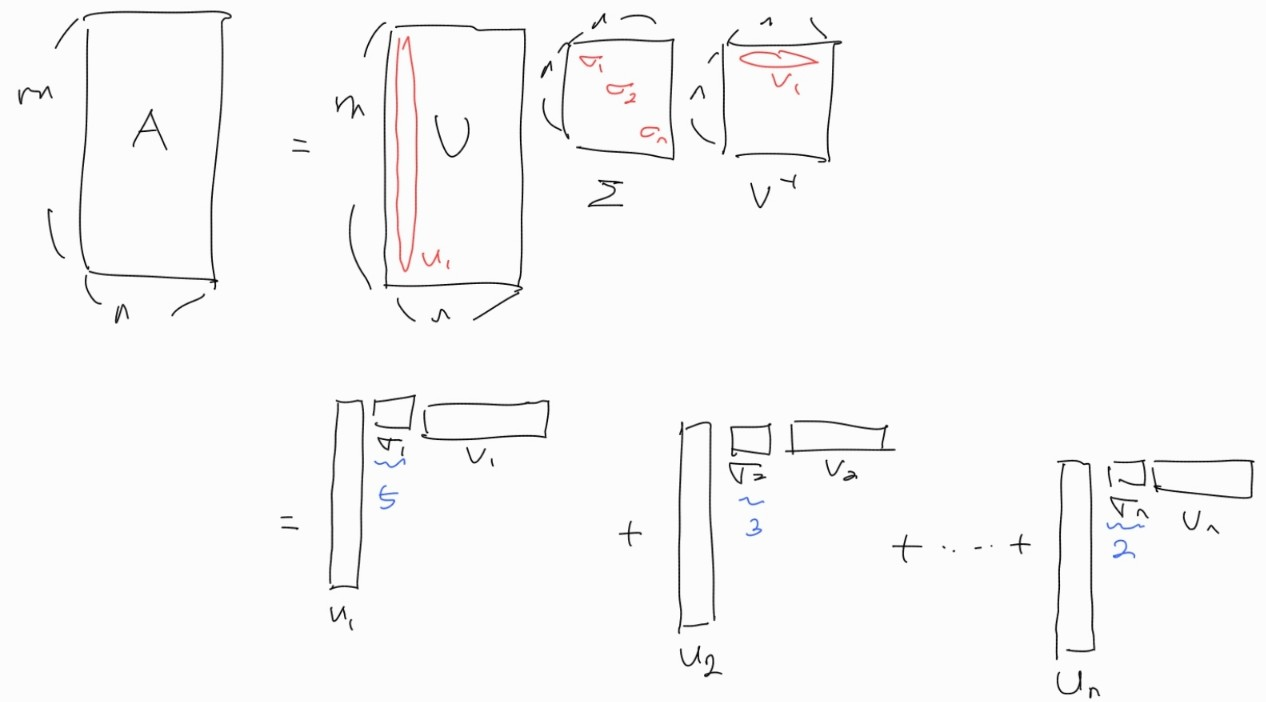
이때, 각각의 시그마값이 가지는 의미를 high level에서 바라보면 A 행렬의 정보량이다. ($u_1 v_1^T$ 에서 각각의 길이는 1이므로 부피가 1이다. 따라서 시그마값 없이는 모두 같은 정보량이라고 말씀을 하셨다.)


시그마값이 즉 행렬 A에 미치는 외적의 영향력이 된다.
즉, 첫 번째 외적이 A에게 5만큼 영향을 끼치게 되고, 전체 시그마의 합이 10이라면 50%의 영향을 주게 된다.

실제로 측정에서의 편향 같은 것은 시그마값이 적은 외적이 정보를 담고 있어서, 이를 제거하여 좀 더 정확한 분석이 가능하다고 한다.

Low-Rank Approximation이 하고자 하는 것은 중요한 몇 개의 시그마를 사용해서 A를 다시 표현하는 것인데, 이건 orthonormal 한 U 행렬에서 일부 column vector를 추출하는 것이다.

아무것도 하지 않았을 경우 A는 orthonormal 한 U의 column vector 수만큼의 차원(Rank) 을 가진다.

하지만 차원을 일부 중요한 U의 column vector들만 사용해서 A를 표현한다면 그만큼 차원은 낮아지게 된다.

그럼 어떻게 중요한 column vector를 찾아내서 Optimal하게 이 방법을 수행할까?

Optimal한 Low-Rank는 다음 식으로 계산할 수 있다.

$\hat A_r=argmin_{A_r}||A-A_r||_F$

여기서 F는 행렬의 원소의 제곱의 합을 나타낸다.

Dimension - Reducing Transformation

데이터의 차원을 줄여서 정보를 축약하는 변환을 수행한다.

정보 추출 행렬을 G 라고 하자.

$Y=G^T X$
X = (m , k), Y = (r, k) G = (m, r)

여기서 k는 data의 개수이고 m과 r은 각각 feature의 개수이다.

위 변환을 수행하면 m개의 feature를 가진 데이터가 r 개의 feature를 가진 data로 변환된다.

이때 우리가 변환을 잘 시켰는지의 기준은 데이터 간 similarity가 잘 보존되느냐를 기준으로 삼는다.

따라서 Optimal한 식은 다음과 같이 나타내어 진다.

$\hat G=argmin_G||S-X^TGG^TX||_F$

이때 S는 변환 전 y로 계산한 데이터 간 similarity다.

이 식을 풀기 전에 의미를 좀 더 생각해보자.

정보 추출 벡터의 row vector가 비슷한 방향을 가리키게 되면 데이터는 비슷한 정보가 추출되게 된다.

정보 추출 벡터의 row vector를 모두 orthogonal 하게 만들면 정보의 중복이 없어지고 적은 row vector로도 모든 정보를 추출할 수 있게 된다.

따라서 정보 추출 행렬의 row vector를 orthogonal vector를 찾는 것이 중요하다.

이때 X를 특이값 분해하여 얻어낸 orthogonal 한 행렬 U의column vector 들이 Dimension-Reducing의 Optimal한 해가 된다.

만약 3차원으로 줄이고 싶다면 시그마 값이 큰 순서대로 u의 column vector 3개로 G를 만들면 된다.