15. 특이값 분해 (SVD)

본 게시글은 주재걸 교수님의 인공지능을 위한 선형대수 강의를 듣고 정리한 내용입니다.
https://www.boostcourse.org/ai251/joinLectures/195088

Notation

Scalar : 소문자
Vector : 굵은 소문자 (기본 형태가 column vector)
Matrix : 대문자
Col A (Column space of A) : A의 열벡터들이 만드는 span
Row A (Row space of A) : A의 행벡터들이 만드는 span
Nul A (Null Space of A) : $A\bold x = 0$을 만족하는 x의 집합

핵심

• 특이값 분해 (모든 행렬에 대해 적용 가능)
  • $A=U\Sigma V^T$
  • $U,\Sigma,V$ 구하는 법:
    $AA^T,A^TA$ 를 각각 고유값 분해
  • $AA^T,A^TA$가 Symmetric Positive Definite Matrics라 고유값 분해로 구할 수 있음

특이값 분해 (Singular Value Decomposition)

우리가 이전에 배운 고유값 분해는 정사각행렬을 세 개의 행렬로 쪼개는 것이었다.

반대로 특이값 분해는 정사각행렬 뿐만 아니라 직사각행렬에서도 적용이 가능하다. 또한 정사각행렬 중 고유값 분해가 되지 않는 정사각 행렬에서도 적용이 가능한 방법이다.

특이값 분해의 기본 형식은 다음과 같다.

$A = U\Sigma V^T$

• A = m x n 행렬
• U는 orthonormal한 m x m 행렬
• Sigma는 m x n 의 거의 대각행렬 (i!=j 일 경우 모두 0)
• V는 orthonormal 한 n x n 행렬

cf) 고유값 분해

$A = VDV^{-1}$

• A = n x n 정사각행렬
• V 고유벡터로 이루어진 정사각행렬
• D는 고유값으로 이루어진 대각행렬

특이값 분해를 그림으로 나타내면 다음과 같다.

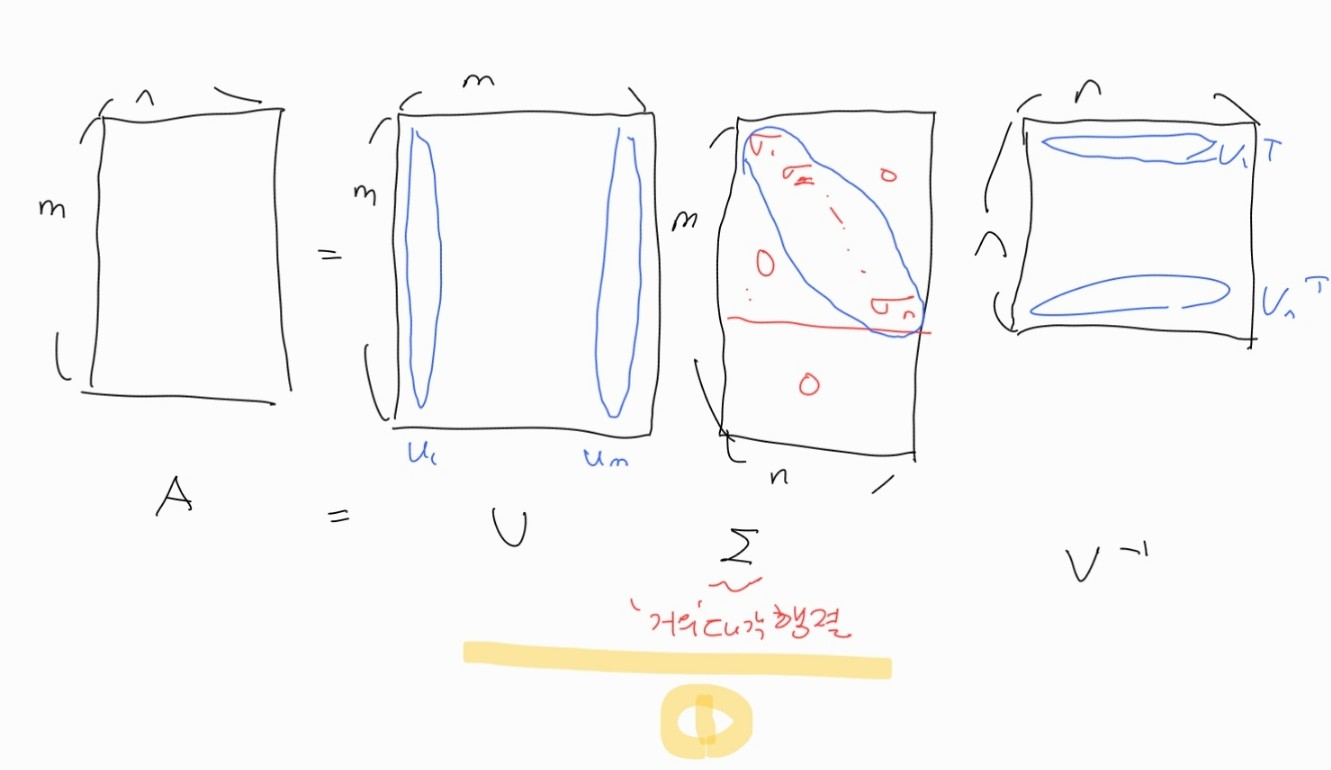
특이값 분해가 만족해야 하는 조건

우리가 특이값 분해를 하기 위해서는 U와 \Simga , V 행렬을 모두 구할 수 있어야 한다.

U와 V를 구하기 위해 특이값 분해 그림의 1번식을 계산해보자.

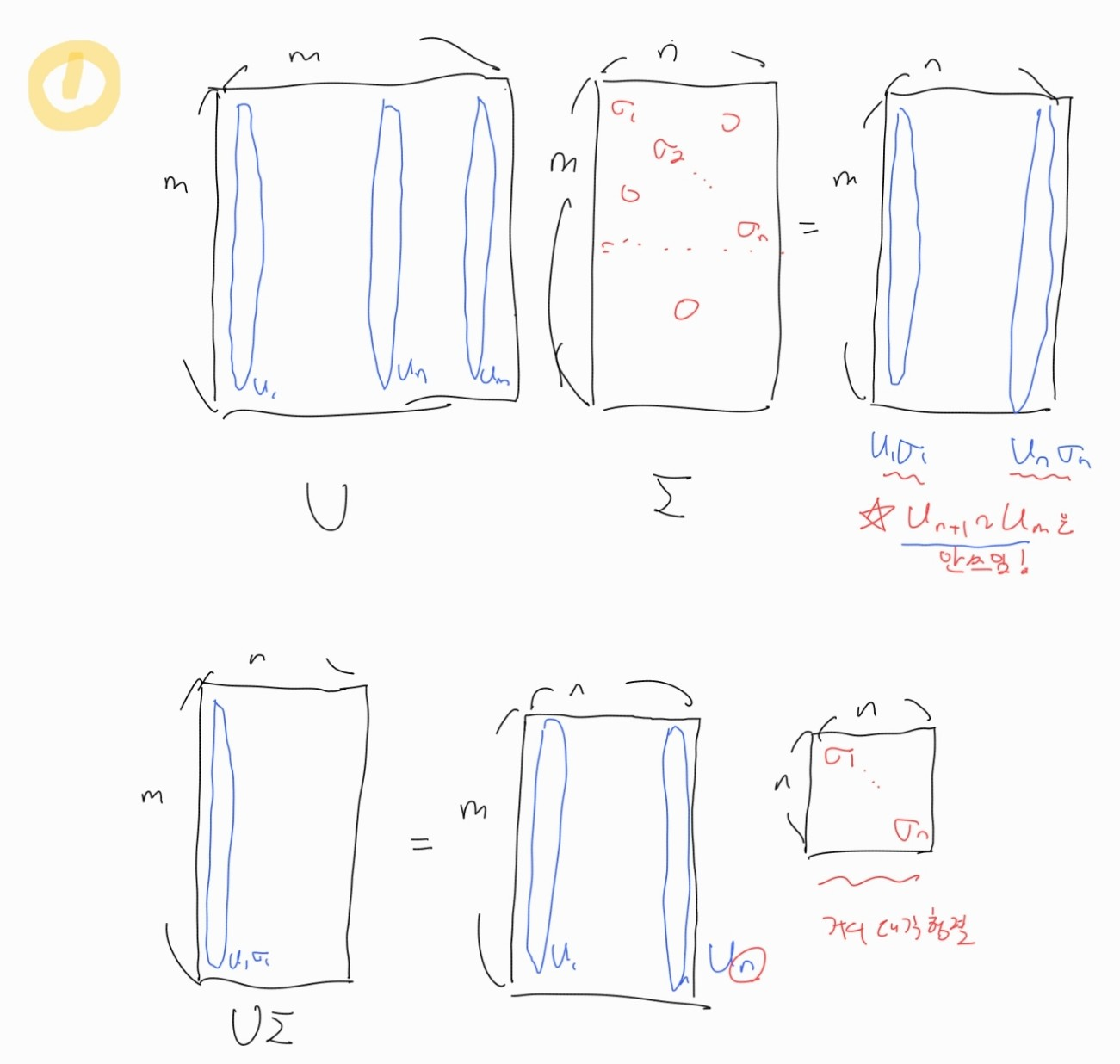
1번식을 계산하면 $U\Sigma$ 부분을 다음과 같이 변형할 수 있고, 그 결과 SVD에서 쓰이지 않는 부분을 제거한 Reduced form을 얻을 수 있다.

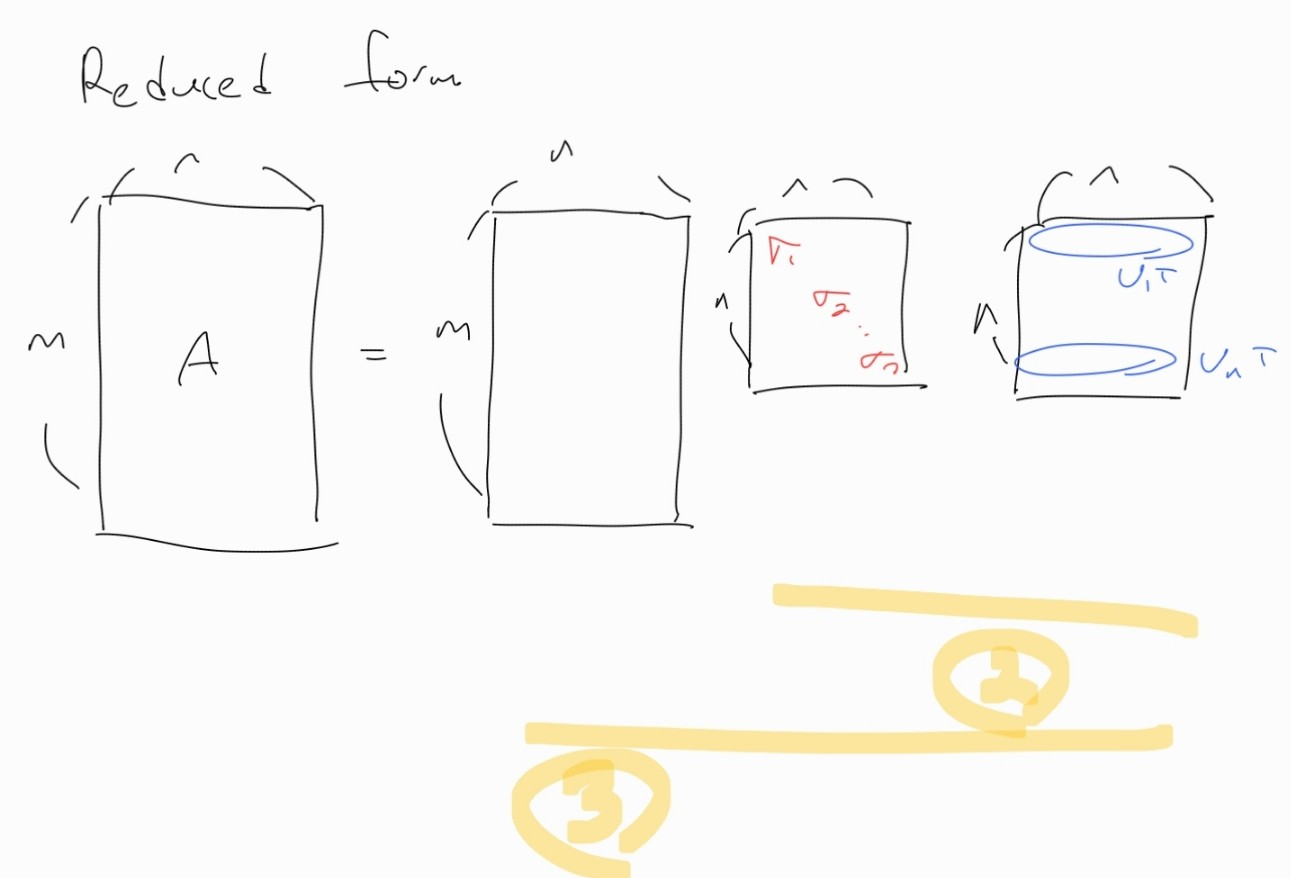
이러한 형태가 우리가 해석하기 쉽다.

2번을 계산하여 행렬의 곱을 column vector들의 선형결합으로 보는 관점을 취해보자.

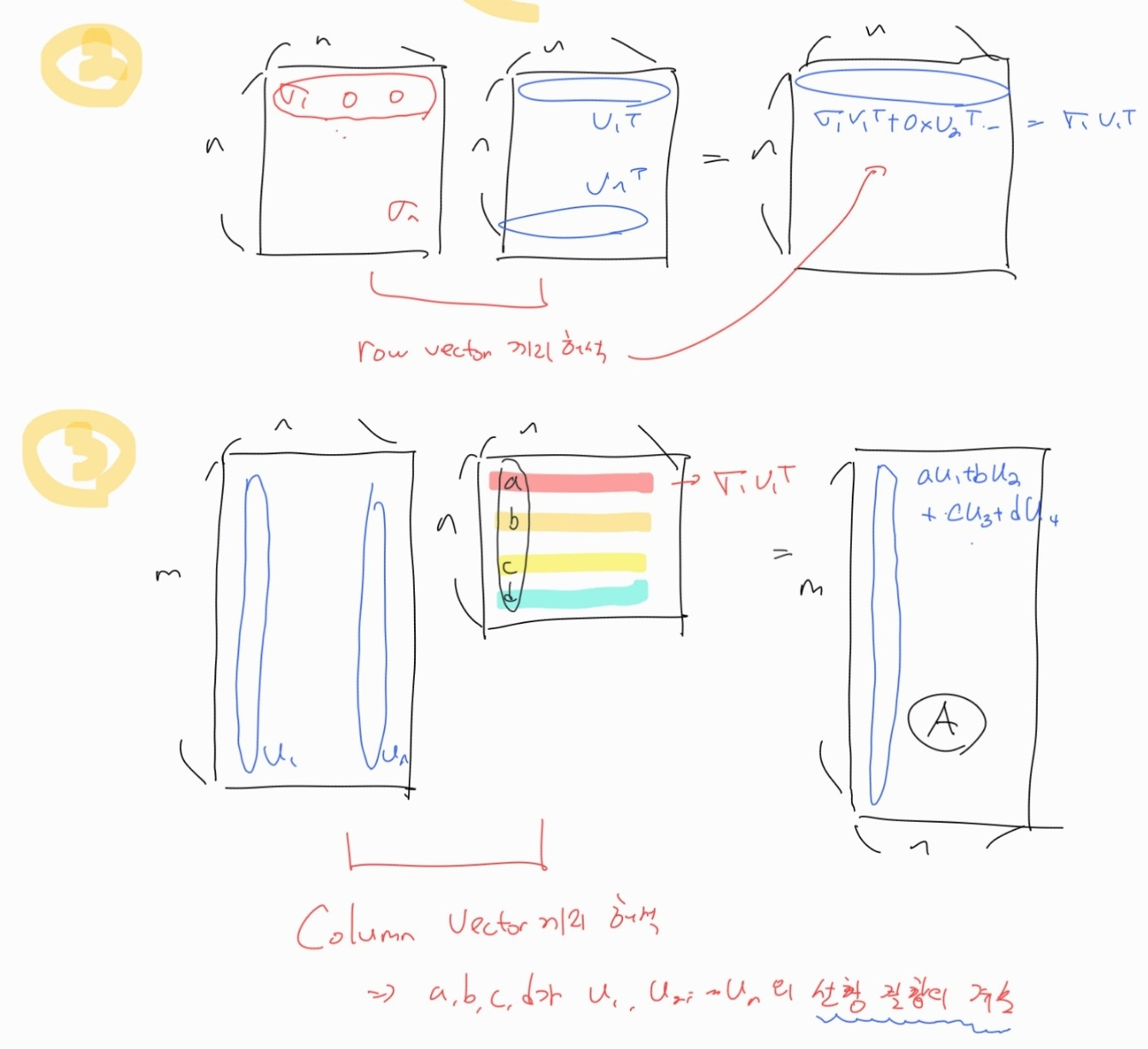
2번 부분을 계산하게 되면 다음과 같이 n x n 행렬을 얻을 수 있다.

이를 3번 식과 결합해서 보면, A의 첫번째 컬럼은 U' (U의 reduced form) 의 컬럼들의 선형결합이 된다. 계수는 당연히 $\Sigma V^T$의 첫 번째 column vector이다.

이는 선형대수에서 자주 쓰이는 두 개의 벡터의 곱을 column vector들의 선형결합으로 보는 방법이다.

위와 같이 A의 모든 column vector들은 U의 column vector들의 선형결합이 되므로 U의 column vector들은 col A의 basis vector가 된다.

그리고 모두 특이값 분해의 조건에 의해 orthonormal 하다.

우리는 예전에 Q-R factorization을 위해 Gram - Schmit orthogonalization 방법을 사용하여 하나의 벡터를 orthonormal한 벡터와 계수의 곱으로 나누었다.

A에 Gram - Schmit orthogonalization을 적용하면 우리는 U와 $\Sigma V^T$를 얻을 수 있다.

V는 어떻게 구할까?

$A=U\Sigma V^T \rightarrow A^T=V\Sigma U^T$에서 $A^T$에 Gram - Schmit를 적용하면 V를 구할 수 있다.
(참고로 이땐, U를 구할 때와 달리 column vector의 선형결합 관점이 아닌 row vector의 선형결합 관점에서 계산해야 한다.)

하지만 Gram-Schmit Orthogonalization 방법은 어떠한 벡터를 처음의 basis로 잡냐에 따라 결과가 유일하지 않다.
그렇다면 U와 V 모두 많은 결과가 나올텐데 어떠한 결과를 잡아야 할까?
-> 이는 U와 V의 관계식을 찾음으로서 해결할 수 있다.

$A=U\Sigma V^T \\ AV =U\Sigma V^TV = U\Sigma$
V는 orthonormal이 전제이므로 $V^TV=I$가 된다.

$AV = U\Sigma$의 의미를 그림을 보면서 살펴보자.

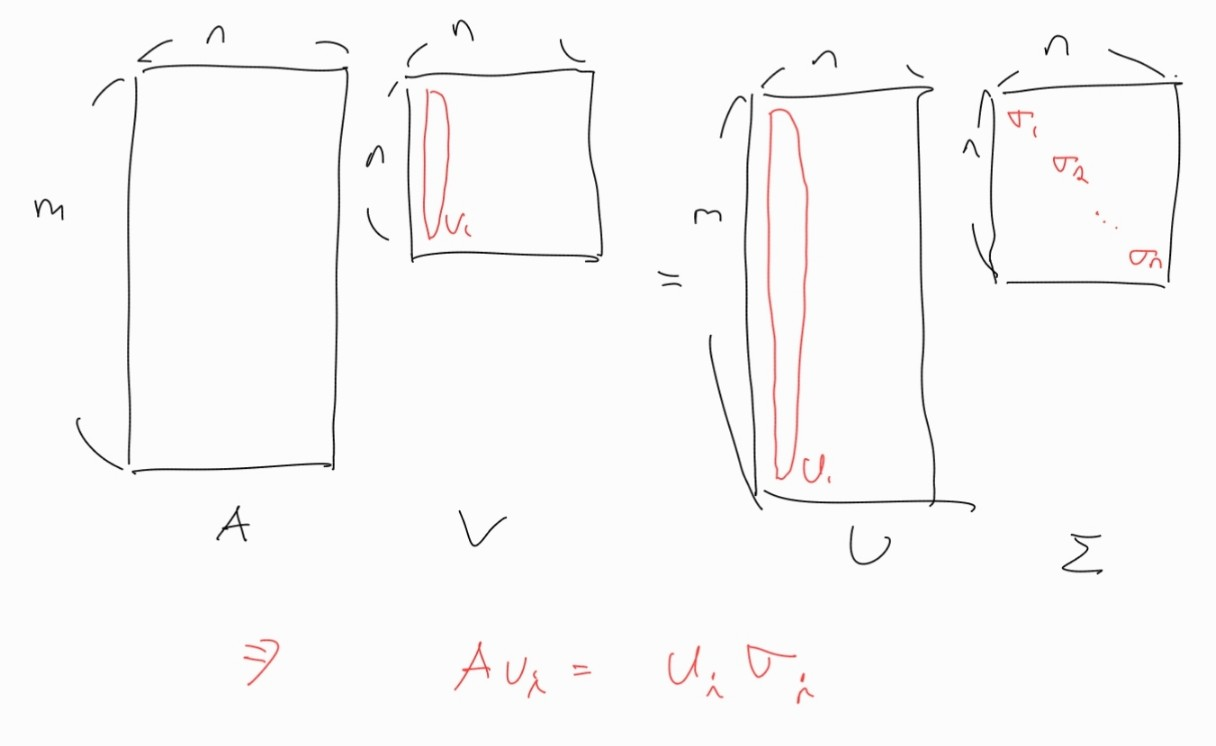
이는 위 그림과 같이 $A\bold v_i=\sigma\bold u_i$를 만족해야함을 의미한다.

위 식은 고유값 분해에서 우리가 봐왔던 식이다.
그래서 SVD를 구하기 위해 고유값 분해를 이용한다.

고유값 분해로 특이값 분해하기

고유값 분해는 기본적으로 정사각 행렬이어야 한다. 고유값 분해를 이용하기 위해 각각 정사각 행렬로 만들어주자.

$AA^T=U\Sigma V^TV\Sigma U^T =U\Sigma^2U^T = U\Sigma^2U^{-1}$ => (m x m)
$A^TA=V\Sigma U^T U\Sigma V^T = V\Sigma^2 V^T =V\Sigma^2 V^{-1}$ => (n x n)

이렇게 2개의 고유값 분해의 첫 번째 조건인 정사각 행렬과, 두 번째 조건인 양 끝에 역행렬 관계인 행렬을 만들었다.

하지만 저 과정이 고유값 분해라고 인정이 되었을 때 정말 U와 V가 구해지는지 확신을 가지기 위해서는 몇 가지 조건이 더 필요하다.

조건

1. 고유값 분해가 가능한가? <=> $AA^T$는 대각화가 가능한가?
2. U와 V가 정말 orthogonal 한가?
3. 고유값 분해의 결과 고유값은 음수도 나온다. $\Sigma^2$ 에서 음수가 나오면 이를 어떻게 해결할 것인가?
4. $AA^T$와 $A^TA$의 결과 $\Sigma^2$이 다르면 어떡할 것인가?

1번 조건은 $AA^T, A^TA$ 모두 Symmetric 하기 때문에, 대각화가 가능하고, 따라서 고유값 분해가 가능하다.

symmetric의 조건 : $AA^T=(AA^T)^T$

symmetric한 행렬은 또한 spectral Theoram에 따라 다음과 같은 성질을 가진다.

Spectral Theoram

• 고유값이 무조건 n개의 실근을 가진다. (A= n x n)
• eigenspace는 모두 수직이다.

따라서 2번 조건도 Spctral Theoram에 따라 성립한다.

3번 조건과 4번 조건을 만족하기 위해서는 Positive Definite Matrics라는 성질이 필요하다.

Positive Definite Matrics

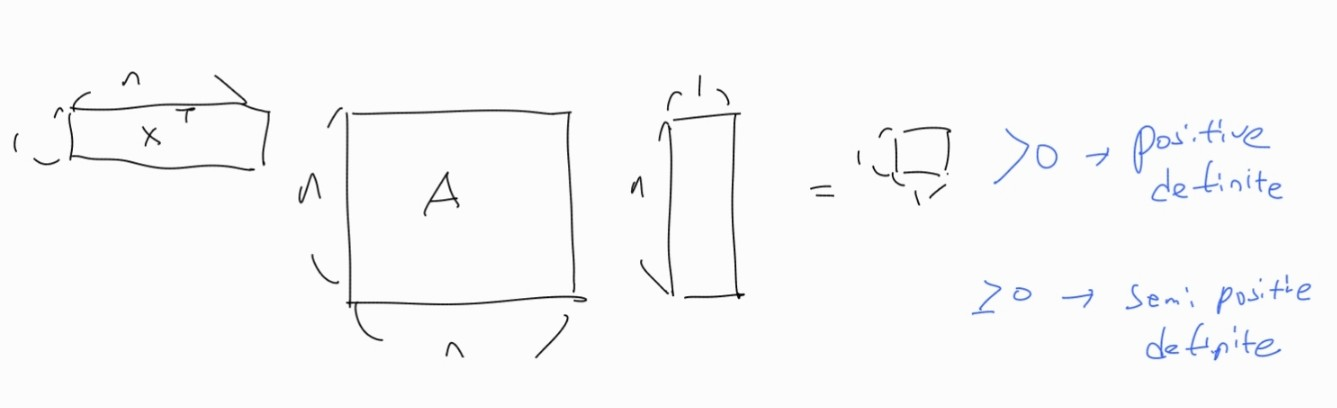
정사각행렬 A가 임의의 행렬 X에 대해 다음을 만족하면 Positive Definite Matrics라 한다.

$\bold x^TA\bold x>0$

만약 Positive Definite Matrics라면 고유값이 항상 양수가 된다.

$\bold x^TAA^T\bold x =(A^T\bold x)^TA^T\bold x=||A^T \bold x||^2 >=0$

그런데 이때 $AA^T, A^TA$ 모두 norm 형태로 나타낼 수 있으므로 항상 양수이다.

즉, 모두 Positive Definite Matrics 이고 고유값은 항상 양수가 된다.

따라서 3번 조건을 만족한다.

종합해보면 $AA^T, A^TA$ 는 Symetric Positive Definite Matrics이다.

4번 조건의 증명은 강의에서 생략되었지만 언제나 만족한다고 한다.

결론적으로 우리는 $AA^T, A^TA$에서 고유값 분해를 진행함으로서 $U,\Sigma,V$를 모두 얻을 수 있다.

$AA^T=U\Sigma V^TV\Sigma U^T =U\Sigma^2U^T = U\Sigma^2U^{-1}$ => (m x m)
$A^TA=V\Sigma U^T U\Sigma V^T = V\Sigma^2 V^T =V\Sigma^2 V^{-1}$ => (n x n)

특이값 분해의 성질

특이값 분해는 고유값 분해와 달리 직사각행렬에서도 가능하다. 또한 고유값 분해의 조건인 정사각행렬, 대각화 가능 행렬에서 대각화가 불가능하더라도 특이값 분해를 사용할 수 있다.