2강 - 해석을 통한 문제풀이(Story Proofs) 및 확률의 공리(Axioms of Probability)

해당 내용은 아래 강좌를 정리한 내용입니다.
https://www.edwith.org/ai152

학습 목표

확률의 naïve한 정의로 접근하기 어려운 경우를 알아내고, story proof를 통한 접근을 할 수 있다. 또한 확률의 non-naïve한 정의를 위한 공리 2가지를 이해하고 적용할 수 있다.

핵심 키워드

• 확률의 naïve 한 정의
• Story proof
• 확률의 non-naïve한 정의의 공리

확률 계산이 헷갈릴 때

• 확률을 계산할 때 기본적인 것은 object에 labeling을 하며 푸는 것이다 예를 들어 같은 검은공이라도 검은공 a, 검은공 b등 이름을 붙이는 것이다.

답이 맞는 지 확인할 때

• 나온 답이 맞는지 확인하는 가장 쉬운 방법은 몇개의 극단적인 수를 대입해보는 것이다.

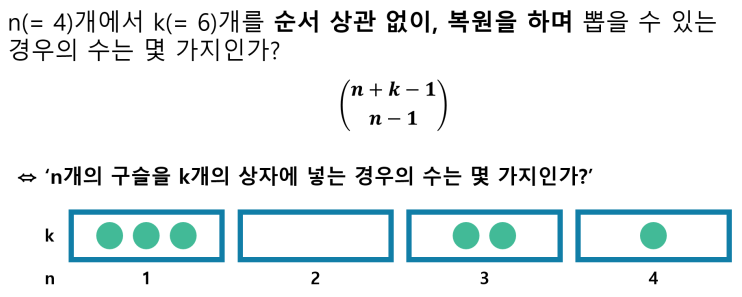
Sampling table에서 replacement and order x인 경우 중복조합이 된다.

n 개의 물체를 중복을 허락하여 k번 뽑는 경우가 대표적인 예이다.

직관적으로 와닿기 위해 구체적인 예를 들자면 6명이서 아이스크림을 먹는데 4종류 중 아무거나 사오는 경우가 된다.

![]

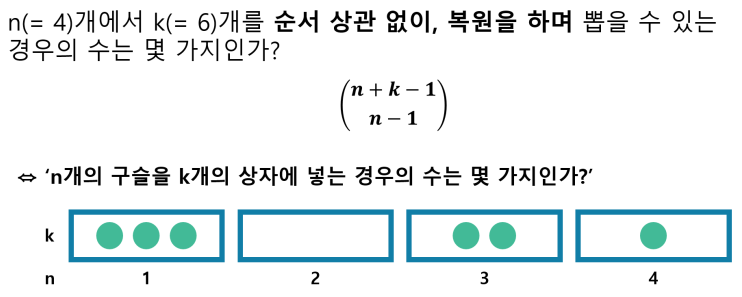
중복 조합 문제는 구분선을 이용하여 해결할 수 있다.

Story proofs (상황 해석을 통한 증명)

1) $\binom{n}{k}=\binom{n}{n-k}$

2) $n\binom{n-1}{k-1}=k\binom{n}{k}$

n명이 지원했는데 k명의 동아리 원을 뽑아야 한다. 근데 이때 k명 중 한명은 동아리 장으로 선출하는 경우의 수를 구해야 한다.

이 경우를 구하는 방법은 2가지이다.

1. 먼저 동아리 장 할 사람을 뽑고 동아리원 k-1명 선발
2. 먼저 동아리원을 뽑고 그 중 한명을 동아리 장으로 선발

3) $\binom{m+n}{k}=\sum_{i=0}^{k} \binom{m}{i}\binom{n}{k-i}$

• m+n명 2개의 그룹에서 k명을 뽑는 것은 m에서 0명 n에서 k명 뽑는 경우와 1,k-1 명 뽑는 경우 등의 합이다.

Non-naive definition of probability

확률 공간(probability space) 은 S와 P로 구성됨.

S는 표본 공간임. P는 정의역을 사건으로 하고 0과 1 사이의 수를 출력하는 함수임.

확률의 공리