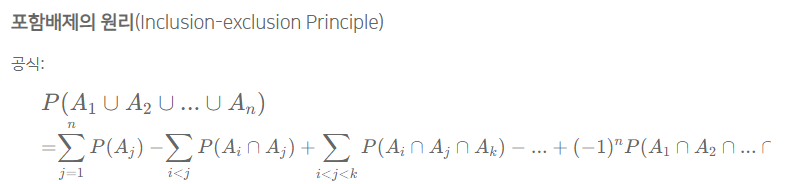3강 Birthday Problem과 확률의 특성

MostlyFor·2023년 1월 9일

목록 보기

3/20

해당 내용은 아래 강좌를 정리한 내용입니다.
https://www.edwith.org/ai152

학습목표

확률의 non-naïve한 정의의 공리를 이용하여 확률의 특성을 증명할 수 있으며, 포함배제의 원리를 이해한다.

핵심 키워드

Birthday problem for naive?? 왜 푼지 모르겠음.

얼마나 많은 사람이 있어야 최소 50%로 같은 생일인 사람이 있을까?

예를 들어) 비둘기 집의 원리에서 366명이 있으면 100%로 같은 생일인 사람이 있다. 즉 답은 366명 보단 작겠다.

$P(no\ match)=1-P(match)$

$P(no\ match)=(\frac{365*364*363...*365-n+1}{365^n})$

실제 정답은 23명일 경우 최초로 50%가 넘음.

50명일 경우는 97%로 같음.

이 문제에 대해 직관적으로 그나마 접근하는 방법은 23명이 있을 경우 (9월22일, 9월21일) 등의 쌍이 23C2개가 나온다는 것임.

확률의 특성은 그냥 공리로 증명하면 됨.

카드가 놓인 위치와 카드가 쓰여있는 숫자가 일치할 확률은?

(단, 카드는 1부터 n까지의 숫자가 적혀있다)

$A_j$ : j번째 카드에 쓰인 숫자가 j인 사건

이 문제는 대칭성 때문에 쉽게 풀 수 있는 문제임.

P(A_j)=\frac{1}{n}\\ P(A_i\cap A_j)=\frac{1*1*n-2!}{n!}=\frac{1}{n(n-1)}\\ P(A_1\cup A_2\cup...\cup A_n)=\binom{n}{1}\frac{1}{n}-\binom{n}{2}\frac{1}{n(n-1)}+\binom{n}{3}\frac{1}{n(n-1)(n-2)}....\\ =1-\frac{1}{2!}+\frac{1}{3!}.... =1-\frac{1}{e}

마지막은 테일러 급수에 의해 근사할 수 있음.

테일러 급수는 확률에서 아주 자주 보이는 패턴임, 분모에 팩토리얼이 있을 경우 먼저 생각해보기!

확률론