해당 내용은 아래 강좌를 정리한 내용입니다.
https://www.edwith.org/ai152
학습목표
전체 확률의 법칙을 이해하고 문제풀이에 적용할 수 있으며, 조건부 독립의 개념을 이해한다.
핵심 키워드
- 전체 확률의 법칙(Law of Total Probability)
- 조건부 확률
- 사전확률과 사후확률(prior, posterior probability)
- 조건부 독립(conditional independence)
문제를 푸는 방법
-
간단한 케이스와 극단적인 케이스로부터 일반화된 값을 추측해보기
-
divied and conquer(분할 정복) 문제를 작은 문제들로 쪼개서 생각해보기
→ 전체 확률의 법칙! (어떻게 나누느냐가 문제를 어떻게 푸느냐임!)
이때 문제를 쪼개서 구하기 위해서는 조건부라는 개념이 필요함.

전체 확률의 법칙이 중요한 점은 B가 일어날 확률을 구하기 위해서 각각이 서로소인 사건으로 구성해 계산한다는점!!
각각이 서로소인 확률은 조건부 확률의 정의를 이용해서 접근할 수 있음!
예제 1) for 조건부 확률
카드 한 벌에서 무작위로 두 장을 뽑았을 때,
i) P(두 장 다 에이스| 에이스를 뽑음)
ii) P(두 장 다 에이스| 스페이드 에이스를 뽑음)
여기선 naive한 확률의 정의가 사용 가능해서 그냥 썼음.
이 문제에서 보면 에이스를 특정했으 뿐인데 확률이 올라감.
왜?? 전체사건의 확률로 생각해볼 수 있음
A를 가지고 있는 것은 특정한 A를 가지고 있는 것을 포함하고 있음 따라서 이건 정확히 전체 확률의 정의로 풀 수 있는 문제임. 전체 확률의 법칙을 적용할 때 중요한 건 가중치임. 가중치를 고려한다면 그런 일이 가능하긴 할듯.
예제 2) for 조건부 확률 (일반적인 편향!)
인구의 1%가 걸리는 병이 있고, 이 병의 검사 결과가 ‘95%의 정확도를 갖고 있다’고 하자. 검사가 양성으로 나왔을 때, 실제로 이 병에 걸렸을 경우는?
실제로 계산해보면 이 검사에서 걸려도 믿을 수 있을 확률은 16%밖에 안됨.
직관을 돕기 위해 1000명이 있다면 대략 10명이 실제 양성이고 950명 중 5%는 가짜 양성 판정을 받게 됨. 대략 50명으로 잡으면 양성 중 진짜 양성은 10/60임.
*베이즈 정리의 일관성 : A라는 믿음에 대해 B, C라는 정보가 주어졌을 때 어느 순서로 갱신해도 확률은 같게 나옴.
여기서 B랑 C는 똑같음.
조건부 확률 문제를 풀며 자주 하는 실수
- P(A|B)P(A∣B)와 P(B|A)P(B∣A)를 헷갈리는 것: ‘조건’과 ‘구하고자 하는 것’을 확실히 알기!
- P(A)P(A) '사전확률‘(prior)과 P(A|B)P(A∣B) ‘사후확률'(posterior)를 헷갈리는 것
- 독립과 조건부 독립을 헷갈리는 것
조건부 독립 (Conditional Independence)
←→ Marginal Independence (일반적인 독립)
-
예시
A : 꽃이 핀다
B : 개구리가 알을 낳는다
C : 봄이 온다
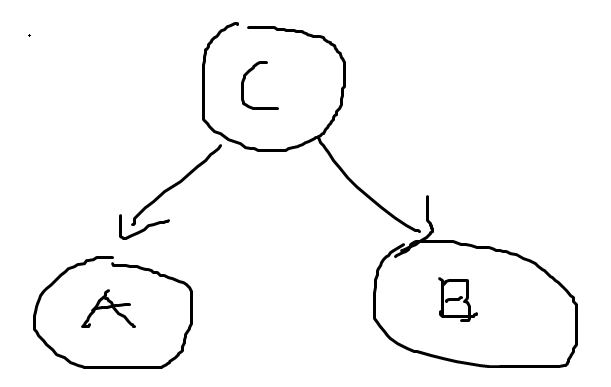
A와 B는 C에 의해서 결정된다. 그림은 다음과 같이 나타낼 수 있다.
이 그림은 베이지안 네트워크와 같다.
를 만족할 때 조건부 독립이 성립한다.
독립이라고 조건부 독립이 성립하지 않고 조건부 독립이라고 해서 독립이라고 할 수 없다!!
-
두 사건이 조건부 독립이면 두 사건은 독립인가?
EX) 체스 경기 - 두 사람이 체스 경기를 하는데 그 사람의 실력과 독립임.
만약 두 사람이 전 경기에서 정보를 얻을 수 없다는 가정 하에서는 각 경기들이 독립임. 그러나 전 경기로부터 정보를 얻을 수 있다면 각 경기들은 확률이 달라짐.
-
두 사건이 독립이면 두 사건이 조건부 독립인가?
EX) 화재 사건 - 화재경보를 일으키는 요인은 불이 나거나 팝콘을 튀기는 경우 밖에 없음
이때 불이 나는거랑 팝콘을 튀기는게 독립으로 일어난다고 가정.
화재 경보기가 울렸다는 가정 하에 팝콘을 튀긴 확률이 0이라면 불이났을 확률이 1임. 즉, 각 사건이 서로에게 영향을 주기 때문에 독립이 아님.