8. Least Square

본 게시글은 주재걸 교수님의 인공지능을 위한 선형대수 강의를 듣고 정리한 내용입니다.
https://www.boostcourse.org/ai251/joinLectures/195088

Notation

Scalar : 소문자
Vector : 굵은 소문자 (기본 형태가 column vector)
Matrix : 대문자

핵심

• 우리가 푸는 대부분의 문제는 일반적으로 방정식의 개수 (데이터의 개수)가 미지수의 개수 (feature의 차원)보다 많아서 해가 없는데, 이것의 근사적 해는 Least Square를 통해 구할 수 있다.
• $\hat \bold x = argmin_\bold x ||\bold b-A\bold x||$
• $A^T(\bold b-A\hat \bold x) = 0$

Least Square

n, m 차원의 행렬에서 n이 더 큰 경우를 의미한다.

이는 방정식의 개수가 미지수보다 많은 경우를 의미하며, 머신러닝에서는 데이터의 개수가 feature의 개수보다 많은 경우를 의미한다.

대부분의 머신러닝 문제는 Least Square를 푸는 문제!

이러한 경우는 m개의 재료 벡터가 만드는 span이 정답을 찾아야 하는데, 이를 예를 들어 다시 말하면, 3차원 공간 상의 한 점을 2차원 공간이 지날 때 정답이 있음을 의미한다.

따라서 대부분의 경우 n이 더 크게 되면 해는 존재하지 않는다.

이렇게 존재하지 않는 경우에 대해 최적해를 구하게 되는데, 이는 Error vector 길이에 따라 결정된다.

최적해는 다음과 같다.

$\hat \bold x = argmin_\bold x ||\bold b-A\bold x||$

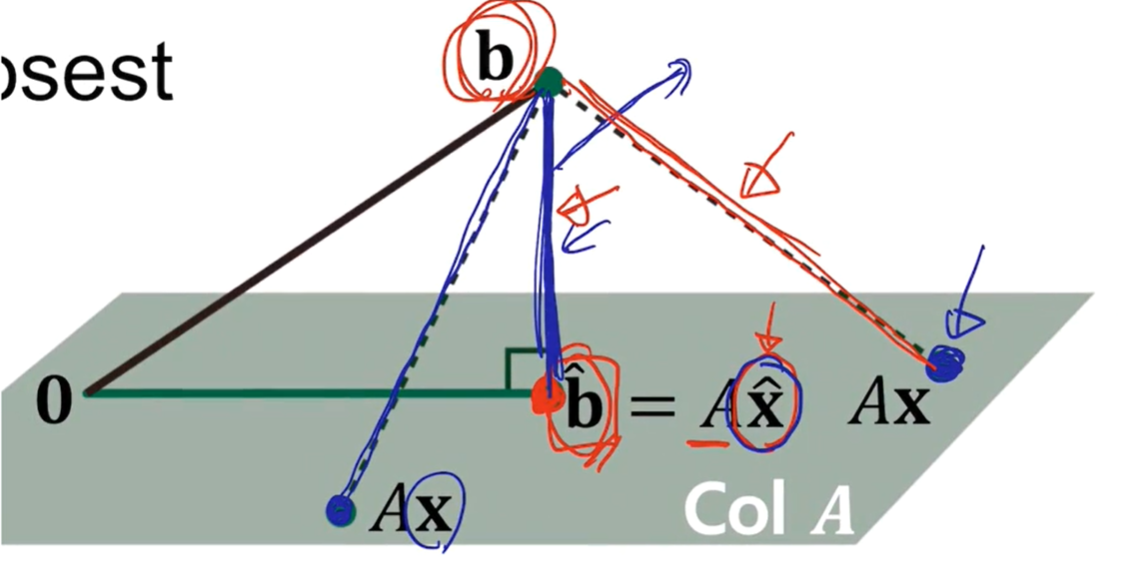
위 식의 의미는 A의 열벡터가 만드는 span에서 b와 가장 가까운 점인 Ax를 만드는 x를 찾는 것이다.

이를 식으로 이해해보자

$(\bold b-A\hat \bold x) \cdot A\bold x=0$ 임의의 x에 대해서 다음이 성립해야 한다.

Ax가 만들어내는 벡터와 모두 내적값이 0이기 위해서는 행렬 A의 열벡터와 모두 내적 0이어야 한다. (Ax가 만들어내는 벡터들은 모두 재료 벡터의 span이다.)

따라서 $A^T(\bold b-A\hat \bold x) = 0$ 인 경우가 최적해가 된다.

Inner product, Norm, Orthogonal

• Inner product : 두 벡터 사이의 각도를 구할 때 주로 쓰임

• Norm : 벡터의 길이를 의미

• Orthogonal : 두 벡터가 수직임을 의미