9. 정규방정식

본 게시글은 주재걸 교수님의 인공지능을 위한 선형대수 강의를 듣고 정리한 내용입니다.
https://www.boostcourse.org/ai251/joinLectures/195088

Notation

Scalar : 소문자
Vector : 굵은 소문자 (기본 형태가 column vector)
Matrix : 대문자
Col A : A column vector들이 만드는 공간 (span)

핵심

• 정규방정식을 norm을 통해서 유도하는 방식
• 정규방정식의 해석
  • $A^TA$의 역행렬이 있으면 해는 유일하다.
  • $A^TA$의 역행렬이 없으면 해는 무수히 많다.
  • $A^TA$가 역행렬을 가지는 조건은 A의 선형 독립이다.
  • 대부분의 머신러닝의 경우는 선형독립으로 역행렬이 있다.
  • 즉 global minimum이 존재한다.

앞에서 Least Square 문제를 푸는 방법으로 정규방정식을 보았다.

$A^TA\hat \bold x = A^T\bold b$

위 식은 다음과 의미상 동치이다.

$\hat \bold x = argmin_\bold x ||\bold b-A\bold x||$

우리는 이 식을 통해서도 같은 식을 유도할 수 있다.

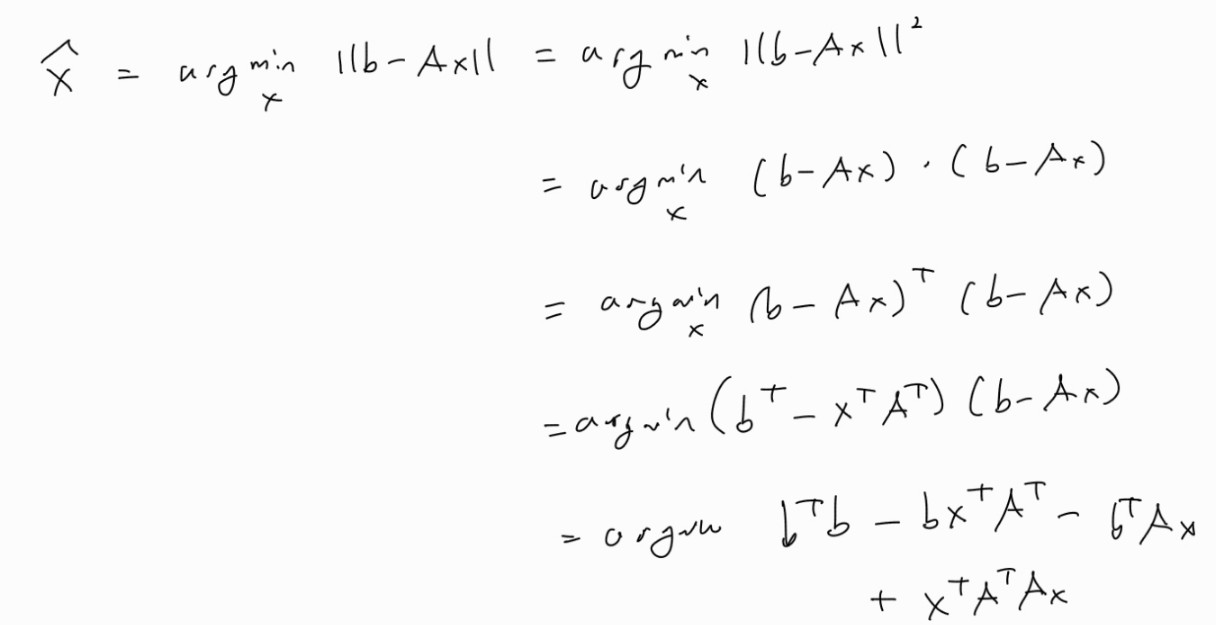
이렇게 얻은 식을 벡터 x에 대해 미분하면 다음과 같다.

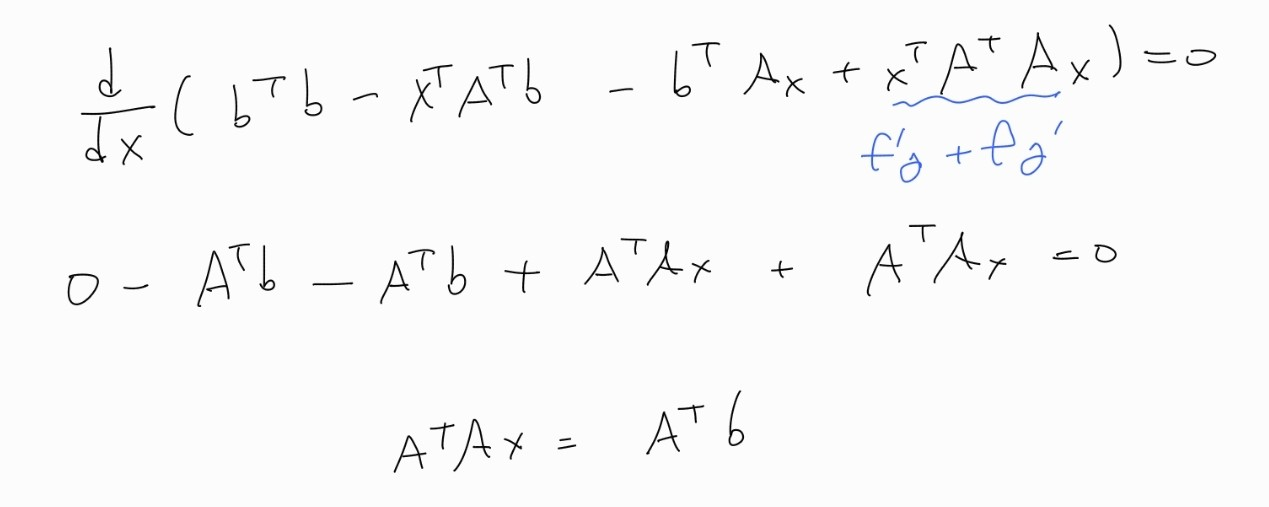
즉, 결론적으로 정규방정식이 나온다.

정규방정식의 해석

$A^TA\hat \bold x = A^T\bold b$

위 식은 새로운 선형변환으로도 볼 수 있다.

만약 $A^TA$가 역행렬이 없다면, 위 방정식의 해는 없거나 무수히 많다.

정규방정식은 위에서 보았듯이 기하학적으로는 A가 만드는 span에 벡터 b가 수선의 발을 내리는 경우 거리가 최소가 되는 점을 찾는 것이다.

이 같은 least square problem 에서는 항상 해가 존재하게 되는데, 엄밀한 증명은 되지 않지만 직관적으로 생각해보았을 때 도형 밖의 한 점에서 도형에 거리가 최소가 되는 점은 도형의 법선 벡터와 나란하므로 도형에 수직이다. 따라서 해는 언제나 하나 이상 존재하게 된다. (교수님도 엄밀한 증명은 pass..)

$A^TA\hat \bold x = A^T\bold b$

즉, 다시 위 식의 해에 대해 생각해보면 정규방정식을 하나의 새로운 선형변환으로 인정하고 $A^TA$의 역행렬이 없다면, 해는 무수히 많거나 없는데, 이미 최소 한 가지가 존재하므로 해는 무수히 많다.

반면, 역행렬이 존재하는 경우는 재료벡터들이 선형독립인 경우로 해가 없거나 하나 있는데, 이미 하나 있는게 증명이 되어 있으므로 해는 단 하나 존재한다.

그렇다면 언제 $A^TA$가 역행렬을 가질까?

$A^TA$가 역행렬을 가지게 되면 수선의 발 $\hat \bold b$는 오로지 한 가지의 표현을 가지는 것이고, 그렇지 않다면 무수히 많은 $\bold x$로 표현이 가능한 것이다.

이는 col A 위에 있는 수선의 발 $\hat \bold b$가 A의 컬럼 벡터들의 선형결합으로 표현되는데 이때 표현이 하나인지에 달려있다.

즉, A의 컬럼 벡터들이 선형독립이라면 표현은 하나만 가능하므로 해가 하나고 이는 $A^TA$ 가 역행렬을 가짐을 의미한다.

근데 실제 푸는 문제에서 선형종속인 경우는 거의 존재하지 않는다고 하신다.