이 글은 Feature Selection 방법 중 Information Gain을 이용하는 방법에 대해 다룬 글이다.

Feature Selection하는 방법에 대해 크게 두 가지 분류로 나눠볼 수 있다.

(분류 기준 - https://medium.com/mlearning-ai/feature-selection-techniques-in-machine-learning-82c2123bd548)

Supervised feature selection vs Unsupervised feature selection

말 그대로 Supervised feature selection은 feature와 target 값의 관계를 관찰하며 feature selction 하는 방법,그리고 Unsupervied feature selection은 PCA처럼 target값과 관계없이 분산을 잘 설명할 수 있는지를 보는 방법이 있다.

Supervised feature selection 방법은 크게 세 가지 접근으로 나눌 수 있는데, 이 글에서 다룰 Information Gain이 속한 Filter-based Approach란 특정 ML 모델이랑 관계 없이 데이터 자체의 속성을 분석하는 방법이다.

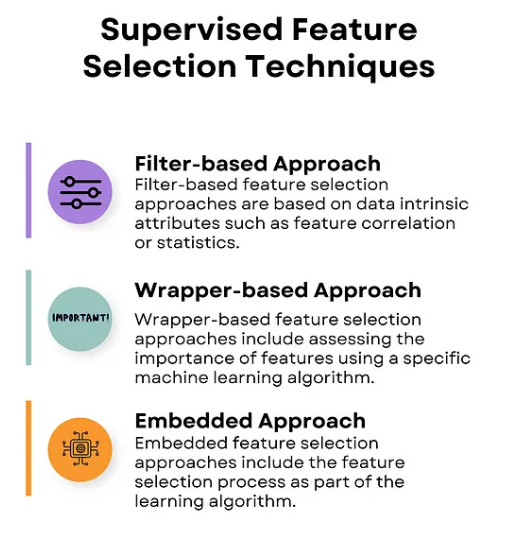Information Gain이란?

Information Gain이란 어떤 feature에 대한 정보를 알았을 때 정보량이 얼마나 줄었는지를 의미하는 것이다.

즉, 정보량의 가중 평균 혹은 혼잡도를 의미하는 Entropy가 얼마나 줄었는지로 표현할 수 있다.

Entropy에 대한 개념은 이전 글에서 다룬 적이 있고 식은 아래와 같다.

Information Gain의 수식은 다음과 같다.

$H(T)$ : 확률변수 T에 대한 엔트로피 (기대 정보량)
$H(T|a)$ : a를 알았을 때 확률변수 T에 대한 조건부 엔트로피

식이 꽤나 직관적이다.

정보 이득 = 원래 정보량과 새로운 걸 알았을 때 정보량의 차이

위에서 조건부 엔트로피가 나왔는데, 조건부 엔트로피의 계산은 다음과 같다.

즉, 조건부 엔트로피는 X로 인해 나뉘어 졌을 때의 정보량의 가중 평균이다.

이해를 위해 머신러닝에서 간단한 이진 분류를 예제로 예를 들어 계산해보자.

우리는 동그라미와 세모를 분리하는게 목적이며 feature는 X와 A가 있다.

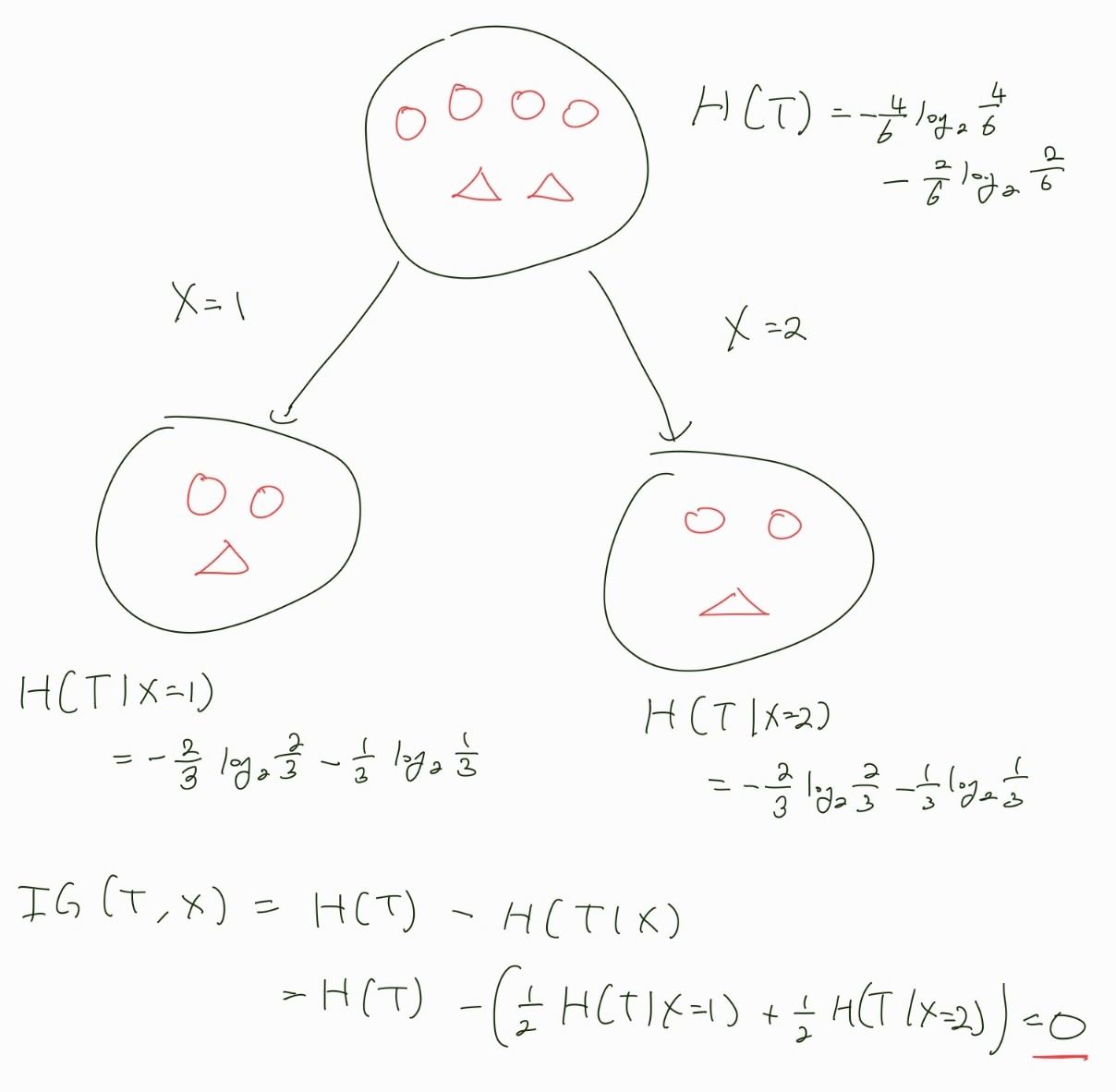
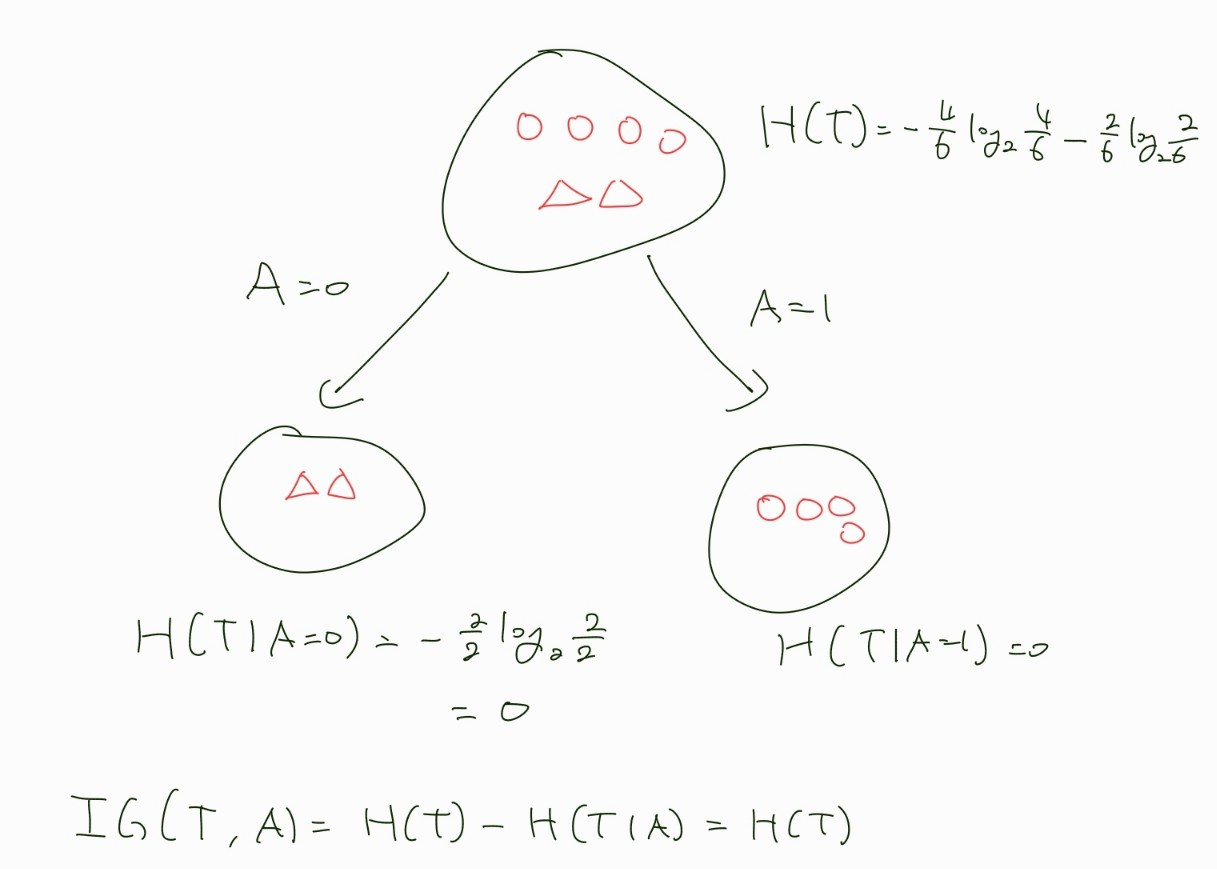
위에서 볼 수 있듯 아무런 관계없는 feature X를 기준으로 분류했을 때 Information Gain은 최솟값, 결정적인 feature A로 분류했을 때 Information Gain은 최댓값이 나왔고 A에 의해 우리의 목표인 동그라미와 세모가 완벽히 분리된 것을 볼 수 있다.

feature x는 어떤 특징이 있어서 아무런 관계 없는 것일까?

Information Gain으로 분류하는 방법

위에서 아무런 관계 없는 feature X를 기준으로 분류했을 때를 Information Gain이 0이 된 것을 확인할 수 있다.

이렇게 정보 이득이 하나도 없던 이유를 살펴보면 X가 T에 대해 독립이기 때문이다.

분류를 위해 X라는 feature를 기준으로 T를 나눴을 때, 분류 이전의 동그라미 세모 비율 66%/33% 와 분류 이후 동그라미 세모 비율 66%/33%가 동일한 것을 확인할 수 있다.

이러한 feature는 분류하는데 아무런 도움이 되지 않는다.

즉, 우리는 Information Gain을 통해서 feature와 종속변수 간의 독립성을 판단할 수 있고, X처럼 높은 독립성을 가진 feature를 제거하는 방식을 생각해볼 수 있다.

이것이 Informaion Gain을 이용하여 Feature를 고르는 방식이다.

주의사항

이 방법은 조심히 다뤄야할 부분이 있다.

요즘 참여하고 있는 경진대회에서 이 방법을 사용했는데, 종속변수에 굉장히 독립적이라고 생각되는 feature가 Information Gain 값이 높게 나왔다.

예상과는 너무 달라서 말이 안된다고 생각하여 찾아보다가 알게 되었는데, 다음과 같은 단점이 있을 수 있다.

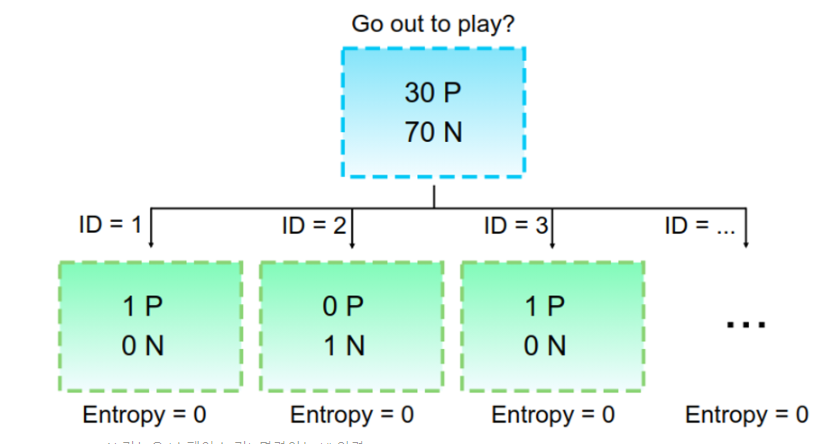
그림은 Feature가 ID인 경우를 나타낸 것인데, 이렇게 feature의 값이 고유한 값인데 이러한 feature를 분류 기준으로 삼았을 경우 분류 이후 Entropy는 0이 된다.

즉, Information Gain이 최대가 되는 것이다.

하지만 우리는 ID와 같은 정보는 큰 의미가 없는 것을 알고 있다.

이런 현상은 feature의 값이 너무 많아서 분기가 너무 많아질 때 발생할 수 있을텐데, 이를 해결하기 위해 Information Gain을 분기의 개수로 나눠주는 방법 등등을 생각했지만, 역시 똑똑하신 분이 먼저 이 문제를 해결했다.

Gain_Ratio

이 방법은 Information Gain에 분기 수에 대한 Panelty를 주는 방식인데, Intrinsic Information을 나눈 값이다.

Intrinsic Information의 식은 다음과 같다.

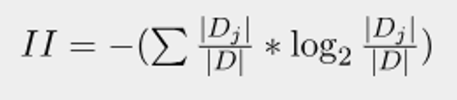
• D : original dataset
• D_j : sub-dataset after bing split (Feature value에 해당하는 개수)

위 식을 잘보면 엔트로피랑 똑같다는 것을 알 수 있다.

엔트로피의 성질 상 분포가 균등할수록 그리고 분기가 많을수록 커지게 되는데 이를 잘 적용한 것이다.

다시 말해 분기된 데이터가 균등할수록 분기의 개수가 많을수록 Intrinsic Information이 커지게 되어, Information Gain에 panelty로 작용하게 된다.

대회에서 이를 적용하여 Information Gain을 Intrinsic Information으로 나누었는데, 나누기 전보다는 합리적인 결과가 나온 것 같다.

실제 사용법

참고로 이 방법은 sklearn의 mutual_info_regression 혹은 mutual_info_clf 를 이용하면 사용할 수 있다. 참고로 Mutual Information과 Information Gain은 같은 개념이다.

참고자료
1. https://en.wikipedia.org/wiki/Information_gain_(decision_tree)
2. https://en.wikipedia.org/wiki/Conditional_entropy
3. https://stats.stackexchange.com/questions/163463/information-gain-and-mutual-information-different-or-equal
4. https://tungmphung.com/information-gain-gain-ratio-and-gini-index/
5. https://medium.com/mlearning-ai/feature-selection-techniques-in-machine-learning-82c2123bd548